Aftershock rate decay induced by postseismic creep: A case study from the MW7.9 Wenchuan earthquake sequence
-
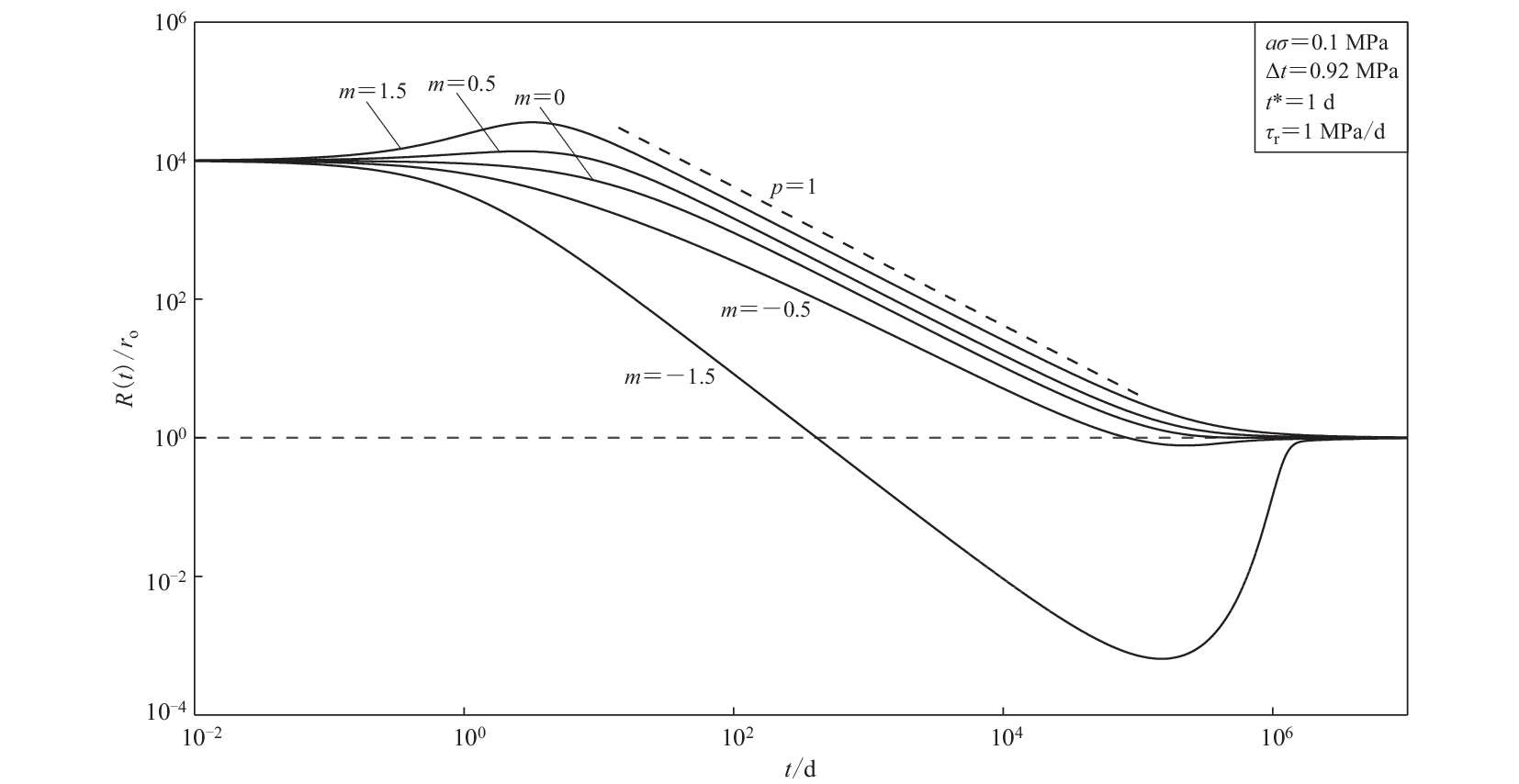
摘要: 基于Dieterich地震活动性理论,本文推导出计算余震发生率和余震累积次数的一般表达式,其中主震后发震断层内部的剪切应力随时间的演化过程遵从Jeffreys-Lomnitz蠕变模型,且与修正Omori定律直接相关。修正Omori定律中的p值与震后断层的短时应力加卸载过程正相关。采用Rubin和Ampuero 给出的震后断层自维持蠕滑模型本文得出计算余震发生率的近似表达式,并对2008年汶川地震序列进行拟合。结果表明,p值的大小直接对应了速率-状态摩擦定律中摩擦参量b/a,而修正Omori定律中的c值则与速率-状态摩擦定律中的临界滑移Dc相关。对于汶川余震序列而言,拟合结果显示b/a约为1.13,Dc约为2—3 cm。Rubin-Ampuero震后自维持蠕滑描述了震后孕震层内部短暂的速率变化特征,是孕震断层演化过程不可缺少的环节。Abstract: Based on the Dieterich seismicity theory, this study derived a general formula used to calculate decay rate and cumulative frequency of aftershocks following a mainshock, of which the shear stress variation in the fault plane follows the Jeffreys-Lomnitz creep law and is directly related to the modified Omori law. The p value in the modified Omori law is positively correlated with post earthquake loading and unloading process of the transient stress. Combined with the postseismic slip model proposed by Rubin and Ampuero, this study obtained approximate formulas to describe the variation of seismicity and to fit aftershock sequence following the 2008 MW7.9 Wenchuan earthquake. The results show that the p value is directly associated with the ratio of b/a, where a and b are the frictional parameters used in rate- and state-dependent friction, and the c value used in the modified Omori law is associated with Dc, a critical creep distance described by rate- and state-dependent friction. For the MW7.9 Wenchuan earthquake sequence, the fitting results indicate the ratio of b/a and Dc are about 1.13 and 2 to 3 cm, respectively. It needs to be emphasized that postseismic creep proposed by Rubin and Ampuero is an inherent stage during earthquake cycle, which describes characteristics of the transient velocity change in seismogenic zone after the mainshock.
-
Keywords:
- aftershock rate /
- postseismic creep /
- stress /
- stressing rate
-
引言
矿震是由开采而产生的一种诱发性地震,随着矿井的开采,井下聚集大量能量并在超过临界点时释放,严重时会造成顶板事故、冲击地压、煤与瓦斯突出等煤矿突发事故(Ursano et al,2006;李长洪等,2009;Grayson et al,2009;陈光波等,2021)。矿山微震信号拾取对于矿震监测和矿山的安全生产具有重要意义。如何快速准确地识别微震事件和如何进行高质量震相拾取成了矿震检测最急迫的问题(Dubey,Barnard,1997)。矿山微震与天然地震有很大的区别,主要表现在:矿山微震频发且震源位置相对较浅,发震位置与台阵仅相隔几千米,台阵接收到的波形数据中P波与S波的到时接近,难以区分;矿震的震动能量相比天然地震小,持续时间较短,但震源深度较浅,发生的大能量微震事件会诱发灾害,造成的危害大;微震数据尽管也有标记实例,但数据集少,不适合大规模数据集的深度学习。
将微震检测系统用于微震的检测和数据的传递,能够采集矿井中的微震信息。然而由于机器震动、人员车辆走动等环境的影响,检测系统采集到的微震信号中会包含大量的噪声,增加事件的识别难度(陈泽等,2020)。长期以来,微震检测和初至到时拾取都是通过人工或低精度自动算法来完成。人工拾取方法可以通过预处理的方式达到极高的精度,但是耗时长,面对大量微震数据时效率低。传统的自动检测方法,如长短时窗能量比法(short time average over long time average,缩写为STA/LTA),该方法应用于不同矿区和不同信噪比的波形数据时具有较大的误差,且准确率不够稳定,严重时甚至会出现检测后仍需人工重新标注的情况,大大增加了人工成本(Akaike,1974;Allen,1982;Vaezi,van der Baan,2015;Zhang et al,2018;王议迎等,2021)。
早在二十世纪九十年代,深度学习就已应用于地震检测,实现了对波形的广义检测(Dai,Macbeth,1995)。深度学习通过大量有标签的样本实例进行训练,可以挖掘出样本中的深层次特征。基于该特点,深度学习在地震领域的应用取得了不错的成绩。Wang等(2021)提出了基于深度卷积神经网络的Dpick神经网络算法,利用深度卷积的特征提取功能实现了较高精度的P波拾取;Zhou等(2019)提出DetNet+PpkNet的事件检测和相位选取算法,利用长短期记忆网络的时序处理功能,能够较好地拾取P波和S波;Zhu和Beroza (2018)基于U-net网络设计的PhaseNet震相拾取算法,可以同时识别P波和S波。然而,相比较天然地震的检测,矿震存在事件检测和震相拾取的精准度需求高、矿震台站采样频率高、提取数据量大及数据集少等问题,为进行深度学习模型的训练和特征提取增加了困难,使得地震学上的深度学习模型无法完美地应用于实际矿震中(周飞燕等,2017;赵洪宝等,2021)。
鉴于此,本文提出了一种针对小样本的矿山微震事件检测和震相拾取的神经网络方法,并结合数据增强方法(Zhou et al,2019;李安等,2020)在数据集较少的情况下达到训练拾取精度;引入自注意力(self-attention)机制,结合卷积神经网络(convolutional neural networks,缩写为CNN)和门控循环单元(gated recurrent unit,缩写为GRU)构建到时拾取模型,提高模型的精度,以期通过上述研究能够快速有效地识别矿山微震事件,并进行高质量P波到时拾取。
1. 方法
1.1 总体架构
本文主要解决微震事件检测和到时拾取的问题,直接通过输入三分量数据来训练完成。如图1所示,首先对数据进行预处理和数据增强,以便检测和识别;之后检测是否存在微震事件,可以通过卷积神经网络模型来完成,与图像识别类似,将数据输入到事件检测模型(主要由CNN构成,简称CNNDet)中,输出分为“噪声”、“事件开始”和“事件中”三类,该部分会对检测到的事件进行P波到时的预拾取;最后,将具有震相振动波形作为时间序列,采用以GRU为主体、自注意力机制为核心的到时拾取模型(由CNN,GRU和自注意力机制构成,简称CGANet)对其进行精确的震相拾取。
1.2 事件检测模型设计
现如今,大部分地震的微震检测都采用噪声和事件组成的二分类卷积神经网络来完成(Tang et al,2021),但这类卷积神经网络由于采样频率低,其提取的事件波形数据量相对较小,而矿震一般采样率高,提取的事件波形数据量大,会为之后的震相拾取增加负担,增加处理数据的时间成本。因此本文采用三分类卷积网络,在噪声和事件中间增加“事件开始”标签,提取该标签所对应的矿震波形,缩小提取事件的波形,加快处理时间,并进行一定程度的到时预拾取。如图2所示,CNNDet主要由CUnit,FD和softmax构成,其中${\rm{Conv}} ( k{\text{×}}s ) $中k代表卷积核,s表示移动步长,${\rm{MaxPool}} ( k{\text{×}}s ) $中k代表池化核。首先利用多个CUnit对波形数据进行特征提取和压缩。为防止过拟合,每个卷积层都用批量归一化(batch-normalization,缩写为BN)实现正则化,并且在每个卷积层之间都使用池化层来实现下采样,以此来压缩数据和参数,每层CNN的通道数分别设为8,32,64,64;之后是FD模块,该模块由全连接层和Dropout构成,作用是将提取的特征进行总结判断输出。由于波形数据是一维时间序列,采用一维卷积进行特征提取。输入的是三分量波形,有三个通道(一个通道代表一个分量)。最后使用softmax激活函数输出标签的概率,并将检测到的事件进行提取输入到CGANet中。
每层卷积的激活函数为LeakyReLU,形式为:
$$ {\rm{LeakyReLU}} = \max ( 0.25 x , x ) {\text{.}} $$ (1) 1.3 到时拾取模型设计
CGANet的总体框架如图2所示,其主要包括CUnit、GRU单元、注意力机制等几部分。将检测出来的微震事件用CNN来提取特征,CNN通过不断的卷积和池化,从较多的采样点中提取出特征,并将特征维度降低。相比较人眼的识别特征,CNN不仅能够提取一些相对明显的特征,还可以从含噪声的微震事件中提取出一些不易识别的抽象特征,每层CNN的通道数分别设为8,32,64。CNN仅能考虑微震波形的空间信息,而会忽略其中的时间序列,于是在CNN后加入了双向GRU层,每层设置64个神经元,则该网络结构便具有很好的记忆功能,因其拥有无限长的感受野,可提取时序特征。此外,为了能够捕捉时间序列中的依赖关系,充分考虑波形之间不同阶段的状态信息,引入自注意力机制(Vaswani et al,2017;Mousavi et al,2020;李宇等,2023),通过权重参数的调整,使得模型对震相的识别更加精确。最后连接两个全连接层对所有的信息特征进行总结并通过softmax输出。为了防止过拟合,每层都采用Dropout正则化对网络进行优化。
CGANet中的自注意力机制公式表示为:
$$ {\rm{Attention}} ( {\boldsymbol{Q}}, {\boldsymbol{K}}, {\boldsymbol{V}} ) = {\rm{softmax}}\left(\frac{{\boldsymbol{Q}{{\boldsymbol{K}}^{\rm{T}}}}}{{\sqrt {{d_K}} }}\right) {\boldsymbol{V}}\text{,} $$ (2) $$ {\rm{softmax}}{ ( X ) _{ij}} = \frac{{{{\rm{e}}^{{X_{ij}}}}}}{{\displaystyle\sum {{{\rm{e}}^{{X_i}}}} }} \text{,} $$ (3) 式中,Q为当前的特征信息,K为Q下一步可能对应的所有的特征信息,V为权重,${d_K}$为Q和K的维度,当Q=K=V时则为自注意力机制。计算每个特征信息与所有对应信息的关系得分,然后做softmax归一化。自注意力机制中的每个特征值都会和该波形内所有提取的特征信息进行注意力权值计算,学习内部的特征依赖信息以捕捉波形的内部结构。
2. 数据集
本文所用的数据集为2019—2020年山西和辽宁某矿区地面微震监测系统的数据。振动数据波形通过布置在煤矿中的台网设备获取,台站设备由九个宽频带三分量微震台站组成,其空间范围约为6 km×4 km×1 km,原始采样频率为5 kHz。由于矿震发生的位置与台站位置相对较近,震相主要为直达P波。采用的数据为通过人工方式选出的2 278个微震事件。从人工挑选的数据中选取了404条数据作为验证集,其余的1874条数据用于训练集和测试集。
2.1 数据预处理及数据增强
对波形数据集进行预处理。如图3所示,首先采用200 Hz的低通滤波器对其进行滤波,避免高频信号噪声对模型训练的干扰,其次,对数据集进行最大值归一化。采用数据增强方法,根据标签类型,随机选择P波到时在时间窗的位置,并增加不同程度的高斯白噪声,以此来添加更多的数据集和提升模型的泛化能力。本文对训练集和测试集进行了数据增强,产生了8 820条数据用于两个模型的训练和测试。
2.2 界限标签法
本文采用界限标签法来设置数据集的标签。在时间窗里设置一定的界限区域,以该区域为限,分为三种状态,分别为“噪声” 、“事件开始”和“事件中” ,其中: “噪声”用来检测噪声,界限区域内仅有噪声;“事件开始”用来提取事件波形或到时拾取,界限区域内有噪声也有波形; “事件中”是为了检测事件结束并区分到时与事件进行两种类型,界限区域内仅有震动波形。矿震的波形数据采样频率高,本文将时间窗调小,提高检测事件的精度,以免遗漏一些小的矿震波形。CNNDet提取出来的切片时间窗口应该包含明显的噪声和波形震相部分,时间窗大小设为2 s (1万个点),滑动步长为0.4 s (2 000个点),CNNDet训练模型标签选取如图4所示,在滑动窗口中设置一个大小为0.4 s的界限区域,位于滑动窗口0.4 s的位置,该位置可以保证提取标签“事件开始”所对应的时间窗口,该窗口内覆盖了难以识别的震相部分和前后明显的噪声波形部分。
CGANet的训练和测试数据同样使用界限标签法,模型的时间窗口设置为1 s,滑动步长为30个采样点,在滑动窗口中设置一个大小为30个点的界限区域,位于滑动窗口0.3 s的位置,选择15个点的位置作为P波到达时间,确保了理论上最大的拾取精度小于15点(<0.006 s)。
3. 试验测试
3.1 性能测试
本文以神经网络库Keras为基本库函数,基于tensorflow2.0深度学习框架搭建并训练模型。模型训练采用自适应运动估计算法,采用阶梯型学习率来优化计算过程。数据采用小批量32个,小批量数据训练可以使得模型更好地拟合,不容易并行化。两个模型的迭代次数设置为200,损失函数采用交叉熵。本文测量了事件和到时模型在训练和验证过程中的分类精度和损失精度。
为了分析模型的性能,本文在训练过程中计算了测试结果的曲线下面积 (area under curve,缩写为AUC)、精确率(precision)和召回率(recall)。AUC为接受者操作特性(receiver operating characteristic,缩写为ROC)曲线与坐标轴围成的面积。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的模型表现。精确率表示自动拾取算法预测结果的准确度,召回率用于检测自动算法拾取的完整度,二者公式如下:
$$ {\rm{Precision}}{{ = }}\frac{{N_{\rm{TP}}}}{{N_{\rm{TP}} + N_{\rm{FP}}}}\text{,} $$ (4) $$ {\rm{Recall}} = \frac{{N_{\rm{TP}}}}{{N_{\rm{TP}} + N_{\rm{FN}}}}\text{,} $$ (5) 式中,NTP为检测正确波形的次数,NFP为将错误波形检测为正确的次数,NFN为正确波形漏选的次数。如图5所示,通过对不同迭代次数的验证集计算精确率和召回率,评估两个模型的训练进度和性能,结果显示:CNNDet模型迭代到80次后进入平缓期,训练精度收敛到99%以上,测试集精度达到97.33%,该模型最后精确率和召回率都稳定在98%以上;对于CGANet模型,模型的训练精度收敛到95%,测试集精确率低于训练精度,达到94%以上,未出现过拟合情况。
此外,针对模型测试的到时误差,本文增加平均绝对误差(mean absolute error,缩写为MAE)和标准差试验评价指标,MAE能够直观地表现出自动算法的拾取精度,标准差可以展现出波形到时误差的离散程度。为了客观地评估CNNDet+CGANet的实用性和优越性,选取了三种震相拾取算法进行对比:STA/LTA算法、DPick算法和DetNet+PpkNet算法。由于直接使用STA/LTA算法同时进行识别检测和到时估计会出现大量的波形检测遗漏(付继华等,2019),本文先使用CNNDet模型检测矿震事件并提取波形,再使用阈值较小的STA/LTA算法进行到时估计。
以验证集对四个模型进行测试,并将测试的结果进行分析,如表1所示。可见:在高采样的优势下,相比于地震领域的震相识别,各个方法的精度都有不同程度的提升,但传统算法提升较少,所采用的传统STA/LTA算法精确率较低,相对而言,深度学习方法在各方面表现更好。
表 1 本文方法与STA/LTA,DPick和PpkNet的性能比较Table 1. The performance of the proposed method in this study compared with STA/LTA,DPick and PpkNet方法 精确率 召回率 平均绝对误差/s 标准差/s 误差>0.2 s占比 CNNDet+STA/LTA 0.724 0 0.724 0 0.028 115 0.086 968 2.28% DPick 0.854 6 0.847 0 0.027 957 0.060 322 2.74% DetNet+PpkNet 0.878 0 0.871 0 0.019 124 0.051 418 1.36% CNNDet+CGANet 0.948 0 0.948 0 0.014 158 0.051 052 1.14% DPick采用的是深度CNN算法,虽然深度CNN模型具有较为复杂的参数结构,但是其忽略了波形数据中的时间因素,具有较小的感受野,导致其相比较于其它深度学习算法来说精度较低。PpkNet采用的是双向GRU模型,其虽然有良好的感受野,但缺少对波形数据的特征提取,很容易受到噪声的影响。试验结果显示,CGANet的误差均值仅有0.014 s,可见本文算法相比其它三种算法具有更好的震相拾取结果。为了直观地展示本文方法的精确率,将每种方法预测的P波到时误差绘制成直方图,如图6所示,可以看出本文算法相较其它三种算法具有较好的误差分布。
3.2 抗噪性测试
在实际应用中,当背景噪声水平高于微地震信号段时,P波拾取精度可能较低。本文采用Dai和Macbeth (1997)提出的信噪比定义,其计算方法为
$$ {\rm{SNR}} = 10\;{\lg }\frac{{{P_{{\rm{sig}}}}}}{{{P_{{\rm{noi}}}}}}\text{,} $$ (6) 式中${P_{{\rm{sig}}}}$为矿震波形信号,${P_{{\rm{noi}}}}$为噪声信号。传统的STA/LTA是由长短时窗的比值和设置阈值来检测P波到时,其阈值大小直接影响拾取的准确性。如图7所示,在信噪比为9.5 dB的低噪声下,STA/LTA的比值较高,较高的阈值也可以较为准确地识别出P波;但在信噪比为3.1 dB的高噪声下,如果事件的振幅相对较小,P波隐藏于噪声中,STA/LTA将会出现较低的比值,并且难以分辨P波和S波,具有极高的误检性,只有选出较为合适的阈值才能正确拾取P波。本文算法相较于传统方法具有更高的精确率,且不受阈值和S波的影响。
为了突出算法的泛化能力,将其在不同噪声下与两个深度学习算法进行抗噪性测试。矿震属于近震波形,大部分的波形起始都有较为明显的振幅变化,如图8所示,在噪声相对较小的情况下,三种模型都表现出了较为精确的到时估计结果,增加了噪声后,三种算法都表现出了不同程度的影响,本文算法受到的影响较小。DPick采用的深度卷积算法的精度受限于其感受野,使得到时拾取结果不稳定,但由于其具有提取特征的性质,可以使其具有一定的抗噪性。PpkNet中有较大的感受野,可以在噪声较小的情况下有较好的性能,但由于缺少提取特征的功能,噪声对其影响最大,当信噪比为2.2 dB时,容易出现拾取错误或漏选等问题。本文算法也受到了一定程度的影响,但相对于其它模型来说,效果较好。
4. 结果与分析
在矿震检测和识别中,往往需要对数据进行实时处理和分析,为此,本文使用该方法对连续数据进行了识别和处理,针对2020年7月山西某矿的五个台站的数据流进行事件检测和P波到时拾取。图9展示了7月11日8:58—9:17对某个台站数据的处理情况,其中CNNDet将检测到的两个矿震事件的起始和结束时间标记出来,之后CGANet进行精确的到时拾取。将卷积、门控循环单元和注意力机制的优势相结合,摒弃了深度卷积神经网络所带来的感受野和特征丢失问题,并在门控循环单元的基础上引入了注意力机制,提取矿震波形内部的特征关系,取得了较好的效果。
数据集和深度学习网络模型是相辅相成的。不同的训练集会出现不同的效果,矿震数据相较于地震数据数量较少,导致一些在地震上应用较好的深度学习方法无法应用于矿震的震相拾取,如PhaseNet,U-Net (Ronneberger et al,2015;赵明等,2019;张逸伦等,2021)。由于矿震的数据集问题,本文选取的训练集设置针对性的标签,在拾取过程中使滑动步长等于界限区域大小,根据界限区域的大小,使用平移和加噪的方式进行数据增强。仅使用1 874个事件数据通过数据增强方式生成8 820条数据用于模型的训练,远远少于类似方法所需的数百万条记录(Perol et al,2018;Saad,Chen,2021)。
为了探究各种到时拾取算法对震源定位的影响,本文对同一事件使用STA/LTA,DPick,DetNet+PpkNet和本文算法来提取矿震P波到时,然后使用粒子群定位算法(Chen et al,2009)对震源进行精定位,得到的使用STA/LTA,DPick,DetNet+PpkNet算法的定位误差分别为95.75,91.50和55.26 m,而使用本文算法的定位误差可达41.67 m,明显优于其它算法。
由于矿震所需的到时拾取精度较高,本文采用两个模型进行拾取:使用CNNDet模型进行到时预估计,给出到时范围,然后再用CGANet模型进行P波估计。总体方法步骤比较复杂,但拾取精度提高,能够有效地拾取P波震相;该方法采用少量数据集训练,增加数据量是否会提升方法的性能仍待研究证实;从实际的连续波形处理中可以看出,虽然该方法可以对事件进行准确检测,但对于事件结束点的提取仍存在一定的误差,如何精准地提取事件结束点以及简化模型等方面仍需进一步研究。
5. 结论
传统的矿山微震P波到时拾取算法存在P波缺失、P波拾取精度低等问题,本文引入了深度学习方法进行研究,提出了一种融合门控循环单元和自注意力机制的矿山微震P波到时拾取方法,为矿山微震监测和冲击地压等灾害的准确识别提供了一种新方法。针对矿震数据的优缺点,提出一种新的数据分类方式,仅利用数据增强的少量数据进行模型训练,即可实现较高精度的P波到时拾取。CNNDet在测试集上的事件检测精确率和召回率都达到98%以上,CGANet对于P波到时估计的误差均值和标准差分别为0.014 s和0.051 s。对比结果表明,本文算法在性能、精度和抗噪性等方面均优于STA/LTA,DPick和PpkNet等算法,且在实际震源定位中,应用本文算法的定位误差明显小于其它算法。随着矿山开采的工业化,微震监测系统将会采集更多的矿山微震数据,未来可考虑增加数据集,简化方法,不断优化神经网络模型。深度学习方法在实时微震监测、矿震预警等方面将会发挥越来越重要的作用。
-
图 1
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
Figure 1.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
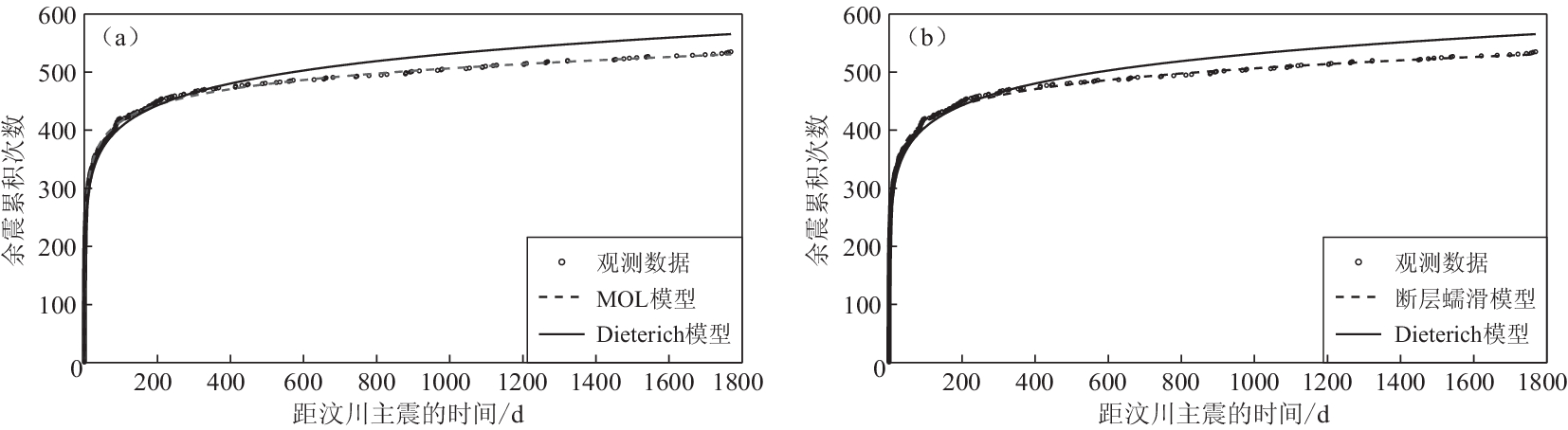
图 3 余震累积次数和不同模型最佳拟合曲线的对比
(a) MOL模型与Dieterich模型;(b) 断层蠕滑模型与Dieterich模型
Figure 3. Comparison between the temporal distribution of the cumulative number of triggered events corresponding to real data and the best fits obtained by the different models
(a) MOL model and Dieterich model;(b) Postseismic slip model and Dieterich model
表 1 MOL模型参数拟合值
Table 1 Fitted parameters in the MOL model
K p c/d RMS $ {r_{\rm d}^2}$ 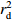
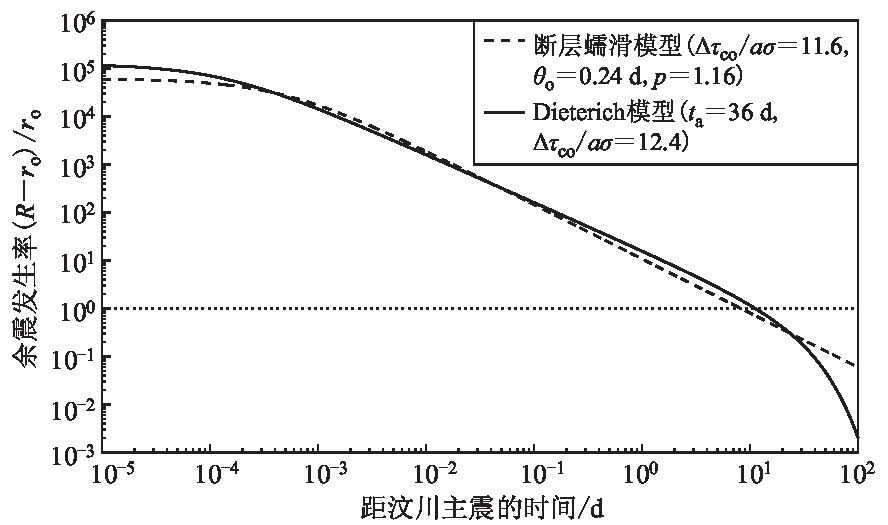
76.290 796 433 386 3 1.129 714 921 398 86 0.174 700 213 127 629 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 201 251 5 1.129 714 919 607 34 0.174 700 212 134 727 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 599 558 6 1.129 714 921 574 52 0.174 700 214 565 022 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 420 031 1 1.129 714 920 241 93 0.174 700 213 526 721 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 407 508 2 1.129 714 920 303 60 0.174 700 213 369 922 4.723 176 877 126 94 0.999 064 715 754 963 76.290 795 889 337 1 1.129 714 918 858 40 0.174 700 210 045 648 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 203 779 0 1.129 714 919 793 27 0.174 700 211 916 160 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 358 633 6 1.129 714 920 749 10 0.174 700 212 952 576 4.723 176 877 126 94 0.999 064 715 754 963 76.290 796 339 850 3 1.129 714 920 639 84 0.174 700 212 665 134 4.723 176 877 126 93 0.999 064 715 754 963 76.290 796 251 218 9 1.129 714 919 679 88 0.174 700 212 577 751 4.723 176 877 126 94 0.999 064 715 754 963 注:表中K∈[0,500];p∈[0,5];c∈[−10, 10] ( Utsu et al,1995 ;Utsu,2002;Hainzl et al,2016) 。表 2 Dieterich模型参数拟合值
Table 2 Fitted parameters in the Dieterich model
ta/d exp[Δτco/(aσ)] Δτco/(aσ) RMS $ r_{\rm d}^2$ 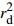
5 882.015 239 530 44 123 970.933 974 009 5.093 319 873 110 68 16.132 130 498 174 8 0.989 089 148 314 182 5 882.014 868 234 99 123 970.963 284 002 5.093 319 975 789 32 16.132 130 498 171 8 0.989 089 148 314 186 5 882.015 309 131 30 123 970.909 997 818 5.093 319 789 117 38 16.132 130 498 174 2 0.989 089 148 314 182 5 882.014 592 899 16 123 970.994 215 420 5.093 320 084 148 10 16.132 130 498 172 7 0.989 089 148 314 184 5 882.014 503 677 40 123 970.987 109 376 5.093 320 059 254 25 16.132 130 498 172 8 0.989 089 148 314 184 5 882.014 976 173 96 123 970.948 098 090 5.093 319 922 590 10 16.132 130 498 169 5 0.989 089 148 314 189 5 882.014 915 449 27 123 970.957 968 035 5.093 319 957 166 45 16.132 130 498 172 2 0.989 089 148 314 185 5 882.015 214 323 03 123 970.935 318 443 5.093 319 877 820 50 16.132 130 498 170 4 0.989 089 148 314 188 5 882.015 150 196 45 123 970.949 854 423 5.093 319 928 742 88 16.132 130 498 170 6 0.989 089 148 314 187 5 882.015 052 767 42 123 970.941 083 807 5.093 319 898 017 70 16.132 130 498 167 5 0.989 089 148 314 192 注:表中ta∈[0,106],exp[Δτco/(aσ)]∈[0,106] (Dieterich,2007; Kame et al,2013 )。表 3 断层蠕滑模型参数拟合值
Table 3 Fitted parameters in the postseismic slip model
θo/d b/a exp[Δτco/(aσ)] Δτco/(aσ) RMS $ r_{\rm d}^2$ 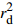
0.174 700 212 670 846 1.129 714 920 608 64 60 844.601 650 449 9 4.784 222 052 123 64 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 212 368 259 1.129 714 920 027 86 60 844.601 626 682 0 4.784 222 051 953 99 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 213 831 794 1.129 714 921 162 83 60 844.601 370 971 4 4.784 222 050 128 78 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 212 381 837 1.129 714 920 578 23 60 844.601 713 419 6 4.784 222 052 573 10 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 212 075 125 1.129 714 919 810 53 60 844.601 679 670 0 4.784 222 052 332 20 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 212 385 557 1.129 714 920 392 20 60 844.601 712 262 3 4.784 222 052 564 84 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 212 418 767 1.129 714 919 972 89 60 844.601 611 131 1 4.784 222 051 842 99 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 213 236 443 1.129 714 920 438 69 60 844.601 424 260 9 4.784 222 050 509 15 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 214 115 631 1.129 714 921 173 05 60 844.601 283 946 5 4.784 222 049 507 62 4.723 176 877 126 94 0.999 064 715 754 963 0.174 700 211 246 645 1.129 714 919 459 10 60 844.601 866 461 2 4.784 222 053 665 47 4.723 176 877 126 94 0.999 064 715 754 963 注:表中θo∈[0,1],b/a∈[0,5],exp[Δτco/(aσ)]∈[0,106] (Dieterich,2007)。 -
陈学忠, 李艳娥, 郭祥云. 2008. 2008年5月12日四川汶川8.0级地震前后震源区应力水平估计[J]. 国际地震动态, (6): 1-3. Chen X Z, Li Y E, Guo X Y. 2008. Estimation of the stress levels in the focal region before and after the May 12, 2008 Wenchuan, Sichuan earthquake with MS8.0[J]. Recent Developments in World Seismology, (6): 1-3 (in Chinese).
陈运泰, 杨智娴, 张勇, 刘超. 2013. 从汶川地震到芦山地震[J]. 中国科学: 地球科学, 43(6): 1064-1072. Chen Y T, Yang Z X, Zhang Y, Liu C. 2013. From 2008 Wenchuan earthquake to 2013 Lushan earthquake[J]. Science China :Earth Science, 43(6): 1064-1072 (in Chinese).
国家地震科学数据共享中心. 2017. 中国台网统一地震目录[EB/OL]. [2017–09–01]. http://data.earthquake.cn/gcywfl/index.html. Chinese Earthquake Datacenter. 2017. The uniform catalog of China Seismic Network[EB/OL]. [2017–09–01]. http://data.earthquake.cn/gcywfl/index.html (in Chinese).
焦青, 杨选辉, 许丽卿, 王博. 2008. 汶川8.0级地震前后龙门山断裂活动特征浅析[J]. 大地测量与地球动力学, 28(4): 7-11, 37. Jiao Q, Yang X H, Xu L Q, Wang B. 2008. Preliminary study on motion characteristics of Longmenshan fault before and after MS8.0 Wenchuan earthquake[J]. Journal of Geodesy and Geodynamics, 28(4): 7-11, 37 (in Chinese).
申文豪, 刘博研, 史保平. 2013. 汶川MW7.9地震余震序列触发机制研究[J]. 地震学报, 35(4): 461-476. Shen W H, Liu B Y, Shi B P. 2013. Triggering mechanism of aftershocks triggered by Wenchuan MW7.9 earthquake[J]. Acta Seismologica Sinica, 35(4): 461-476 (in Chinese).
田勤俭, 刁桂苓, 郝平, 冯向东, 孙晴. 2009. 汶川8.0级地震及余震破裂的地质构造特征[J]. 地震, 29(1): 141-148. Tian Q J, Diao G L, Hao P, Feng X D, Sun Q. 2009. Earthquake geology of the Wenchuan M8.0 mainshock and its aftershocks[J]. Earthquake, 29(1): 141-148 (in Chinese).
张培震, 徐锡伟, 闻学泽, 冉勇康. 2008. 2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因[J]. 地球物理学报, 51(4): 1066-1073. Zhang P Z, Xu X W, Wen X Z, Ran Y K. 2008. Slip rates and recurrence intervals of the Longmenshan active fault zone, and tectonic implications for the mechanism of the May 12 Wenchuan earthquake, 2008, Sichuan, China[J]. Chinese Journal of Geophysics, 54(4): 1066-1073 (in Chinese).
张勇, 冯万鹏, 许力生, 周成虎, 陈运泰. 2008. 2008年汶川大地震的时空破裂过程[J]. 中国科学: D辑, 38(10): 1186-1194. Zhang Y, Feng W P, Xu L S, Zhou C H, Chen Y T. 2009. Spatial and temporal rupture process of 2008 MW7.8 Wenchuan earthquake, China[J]. Science in China: Series D, 52(2): 145-154.
张致伟, 程万正, 阮祥, 吴朋. 2009. 汶川8.0级地震前龙门山断裂带的地震活动性和构造应力场特征[J]. 地震学报, 31(2): 117-127. Zhang Z W, Cheng W Z, Ruan X, Wu P. 2009. Seismicity and tectonic stress of the Longmenshan fault zone before 2008 Wenchuan MS8.0 earthquake[J]. Acta Seismologica Sinica, 31(2): 117-127 (in Chinese).
Ader T J, Lapusta N, Avouac J P, Ampuero J P. 2014. Response of rate-and-state seismogenic faults to harmonic shear-stress perturbations[J]. Geophys J Int, 198(1): 385-413.
Ariyoshi K, Hori T, Ampuero J P, Kaneda Y, Matsuzawa T, Hino R, Hasegawa A. 2009. Influence of interaction between small asperities on various types of slow earthquakes in a 3-D simulation for a subduction plate boundary[J]. Gondwana Res, 16(3/4): 534-544.
Barbot S, Fialko Y, Bock Y. 2009. Postseismic deformation due to the MW6.0 2004 Parkfield earthquake: Stress-driven creep on a fault with spatially variable rate-and-state friction parameters[J]. J Geophys Res, 114(B7): B07405.
Beeler N M, Lockner D A. 2003. Why earthquakes correlate weakly with the solid Earth tides: Effects of periodic stress on the rate and probability of earthquake occurrence[J]. J Geophys Res, 108(B8): 2391.
Beeler N M. 2004. Review of the physical basis of laboratory-derived relations for brittle failure and their implications for earthquake occurrence and earthquake nucleation[J]. Pure Appl Geophys, 161(9/10): 1853-1876.
Bizzarri A. 2012. What can physical source models tell us about the recurrence time of earthquakes?[J]. Earth-Sci Rev, 115(4): 304-318.
Blanpied M L, Tullis T E, Weeks J D. 1998. Effects of slip, slip rate, and shear heating on the friction of granite[J]. J Geophys Res, 103(B1): 489-511.
Dieterich J H. 1978. Preseismic fault slip and earthquake prediction[J]. J Geophys Res, 83(B8): 3940-3948.
Dieterich J H. 1992. Earthquake nucleation on faults with rate- and state-dependent strength[J]. Tectonophysics, 211(1/2/3/4): 115-134.
Dieterich J. 1994. A constitutive law for rate of earthquake production and its application to earthquake clustering[J]. J Geophys Res, 99(B2): 2601-2618.
Dieterich J H. 2007. Applications of rate- and state-dependent friction to models of fault slip and earthquake occurrence[G]// Treatise on Geophysics, Volume 4: Earthquake Seismology. Amsterdam: Elsevier: 107–129.
Freed A M. 2005. Earthquake triggering by static, dynamic, and postseismic stress transfer[J]. Ann Rev Earth Planet Sci, 33: 335-367.
Freedman D, Pisani R, Purves R. 2007. Statistics[M]. New York: W W Norton & Company Inc: 185–187.
Gomberg J, Reasenberg P, Cocco M, Belardinelli M E. 2005. A frictional population model of seismicity rate change[J]. J Geophys Res, 110(B5): B05S03.
Hainzl S, Marsan D. 2008. Dependence of the Omori-Utsu law parameters on main shock magnitude: Observations and modeling[J]. J Geophys Res, 113(B10): B10309.
Hainzl S, Steacy S, Marsan D. 2010. Seismicity models based on Coulomb stress calculations[EB/OL]. [2010–10–10]. http://www.corssa.org/export/sites/corssa/.galleries/articles-pdf/Hainzl-et-al-2010-CORSSA-Coulomb-models.pdf.
Hainzl S, Christophersen A, Rhoades D, Harte D. 2016. Statistical estimation of the duration of aftershock sequences[J]. Geophys J Int, 205(2): 1180-1189.
He C R, Luo L, Hao Q M, Zhou Y S. 2013. Velocity-weakening behavior of plagioclase and pyroxene gouges and stabilizing effect of small amounts of quartz under hydrothermal conditions[J]. J Geophys Res, 118(7): 3408-3430.
Helmstetter A, Shaw B E. 2009. Afterslip and aftershocks in the rate-and-state friction law[J]. J Geophys Res, 114(B1): B01308.
Hirose T, Shimamoto T. 2005. Slip-weakening distance of faults during frictional melting as inferred from experimental and natural pseudotachylytes[J]. Bull Seismol Soc Am, 95(5): 1666-1673.
Hsu Y J, Segall P, Yu S B, Kuo L C, Williams C A. 2007. Temporal and spatial variations of post-seismic deformation following the 1999 Chi-Chi, Taiwan earthquake[J]. Geophys J Int, 169(2): 367-379.
Hsu Y J, Simons M, Avouac J P, Galetzka J, Sieh K, Chlieh M, Natawidjaja D, Prawirodirdjo L, Bock Y. 2006. Frictional afterslip following the 2005 Nias-Simeulue earthquake, Sumatra[J]. Science, 312(5782): 1921-1926.
Huang Y, Wu J P, Zhang T Z, Zhang D N. 2008. Relocation of the M8.0 Wenchuan earthquake and its aftershock sequence[J]. Science in China: Series D, 51(12): 1703-1711.
Ide S, Takeo M. 1997. Determination of constitutive relations of fault slip based on seismic wave analysis[J]. J Geophys Res, 102(B12): 27379-27391.
Jia K, Zhou S Y, Zhuang J C, Jiang C S. 2014. Possibility of the independence between the 2013 Lushan earthquake and the 2008 Wenchuan earthquake on Longmenshan fault, Sichuan, China[J]. Seismol Res Lett, 85(1): 60-67.
Kame N, Fujita S, Nakatani M, Kusakabe T. 2013. Effects of a revised rate- and state-dependent friction law on aftershock triggering model[J]. Tectonophysics, 600: 187-195.
King D S H, Marone C. 2012. Frictional properties of olivine at high temperature with applications to the strength and dynamics of the oceanic lithosphere[J]. J Geophys Res, 117(B12): B12203.
Kisslinger C, Jones L M. 1991. Properties of aftershock sequences in southern California[J]. J Geophys Res, 96(B7): 11947-11958.
Mainardi F, Spada G. 2012. On the viscoelastic characterization of the Jeffreys-Lomnitz law of creep[J]. Rheol Acta, 51(9): 783-791.
Marone C. 1998. Laboratory-derived friction laws and their application to seismic faulting[J]. Ann Rev Earth Planet Sci, 26: 643-696.
Marone C J, Scholtz C H, Bilham R. 1991. On the mechanics of earthquake after slip[J]. J Geophys Res, 96(B5): 8441-8452.
Mignan A, Woessner J. 2012. Estimating the magnitude of completeness for earthquake catalogs[EB/OL]. [2012-04-01]. http://www.corssa.org/export/sites/corssa/.galleries/articles-pdf/Mignan-Woessner-2012-CORSSA-Magnitude-of-completeness.pdf.
Montesi L G J. 2004. Controls of shear zone rheology and tectonic loading on postseismic creep[J]. J Geophys Res, 109(B10): B10404.
Motulsky H J, Ransnas L A. 1987. Fitting curves to data using nonlinearregression: A practical and nonmathematical review[J]. FASEB J, 1(5): 365-374.
Omori F. 1894. On the after-shocks of earthquakes[J]. J Coll Sci Imp Univ of Tokyo, 7(2): 111-200.
Perfettini H, Avouac J P. 2004. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan[J]. J Geophys Res, 109(B2): B02304.
Paterson M S, Wong T F. 2005. Experimental Rock Deformation: The Brittle Field[M]. Berlin: Springer Science & Business Media: 187.
Perfettini H, Avouac J P. 2007. Modeling afterslip and aftershocks following the 1992 Landers earthquake[J]. J Geophys Res, 112(B7): B07409.
Perfettini H, Ampuero J P. 2008. Dynamics of a velocity strengthening fault region: Implications for slow earthquakes and postseismic slip[J]. J Geophys Res, 113(B9): B09411.
Perfettini H, Avouac J P. 2014. The seismic cycle in the area of the 2011 MW9.0 Tohoku-Oki earthquake[J]. J Geophys Res, 119(5): 4469-4515.
Remy D, Perfettini H, Cotte N, Avouac J P, Chlieh M, Bondoux F, Sladen A, Tavera H, Socquet A. 2016. Postseismic relocking of the subduction megathrust following the 2007 Pisco, Peru, earthquake[J]. J Geophys Res, 121(5): 3978-3995.
Rice J R, Ruina A L. 1983. Stability of steady frictional slipping[J]. J Appl Mech, 50(2): 343-349.
Rice J R. 1983. Constitutive relations for fault slip and earthquake instabilities[J]. Pure Appl Geophys, 121(3): 443-475.
Rubin A M, Ampuero J P. 2005. Earthquake nucleation on (aging) rate and state faults[J]. J Geophys Res, 110(B11): B11312.
Ruina A. 1983. Slip instability and state variable friction laws[J]. J Geophys Res, 88(B12): 10359-10370.
Savage J C, Svarc J L, Yu S B. 2007. Postseismic relaxation and aftershocks[J].J Geophys Res, 112(B6): 1–19.
Savage J C. 2010. Calculation of aftershock accumulation from observed postseismic deformation: M6 2004 Parkfield, California, earthquake[J]. Geophys Res Lett, 37(13): L13302.
Scholz C H. 1990. The Mechanics of Earthquakes and Faulting[M]. New York: Cambridge University Press: 263–265.
Scholz C H. 1998. Earthquakes and friction laws[J]. Nature, 391(6662): 37-42.
Segall P. 2010. Earthquake and Volcano Deformation[M]. Princeton: Princeton University Press: 339–348.
Shen W H, Li Y S, Zhang J F.2017. Hybrid stochastic ground motion modeling of the MW7.8 Gorkha, Nepal earthquake of 2015 based on InSAR inversion[J]. Journal of Asian Earth Sciences, 141:
Shen Z K, Sun J B, Zhang P Z, Wan Y G, Wang M, Bürgmann R, Zeng Y H, Gan W J, Liao H, Wang Q L. 2009. Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake[J]. Nat Geosci, 2(10): 718-724.
Sladen A. 2008. Preliminary result 05/12/2008 (MW7.9), east Sichuan[EB/OL]. [2012–06–21]. http://www.tectonics.caltech.edu/slip_history/2008_e_sichuan/e_sichuan.html.
Tahir M, Grasso J R. 2012. Faulting style controls on the Omori law parameters from global earthquake catalogs[EB/OL]. [2012–01–19]. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.461.1272.
Tsutsumi A, Shimamoto T. 1997. High-velocity frictional properties of gabbro[J]. Geophys Res Lett, 24(6): 699-702.
Utsu T. 1961. A statistical study on the occurrence of aftershocks[J]. Geophys Mag, 30: 521-605.
Utsu T, Ogata Y, Matsu’ura R S. 1995. The centenary of the Omori formula for a decay law of aftershock activity[J]. J Phys Earth, 43(1): 1-33.
Utsu T. 2002. Statistical features of seismicity[J]. Int Geophys, 81: 719-732.
Wang K, Fialko Y. 2014. Space geodetic observations and models of postseismic deformation due to the 2005 M7.6 Kashmir (Pakistan) earthquake[J]. J Geophys Res, 119(7): 7306-7318.
-
期刊类型引用(1)
1. 张毅毅,夏峰,彭达,李磊磊. 黑岱沟矿区场地地脉动测试和分析. 防灾科技学院学报. 2024(03): 42-49 .  百度学术
百度学术
其他类型引用(0)





 下载:
下载: