Stack imaging of non-longitudinal bending line of land reflection seismic data generated by airgun source
-
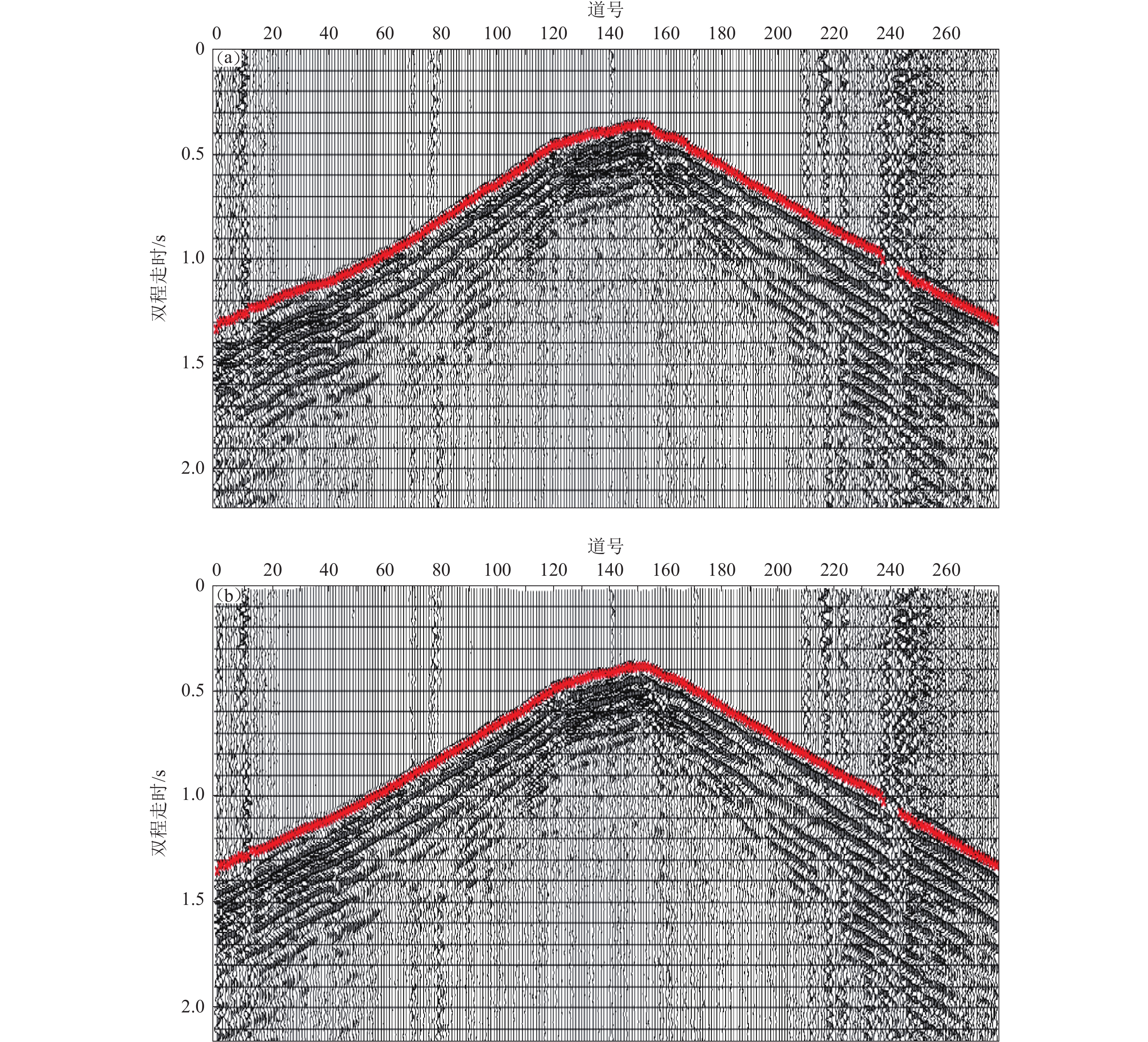
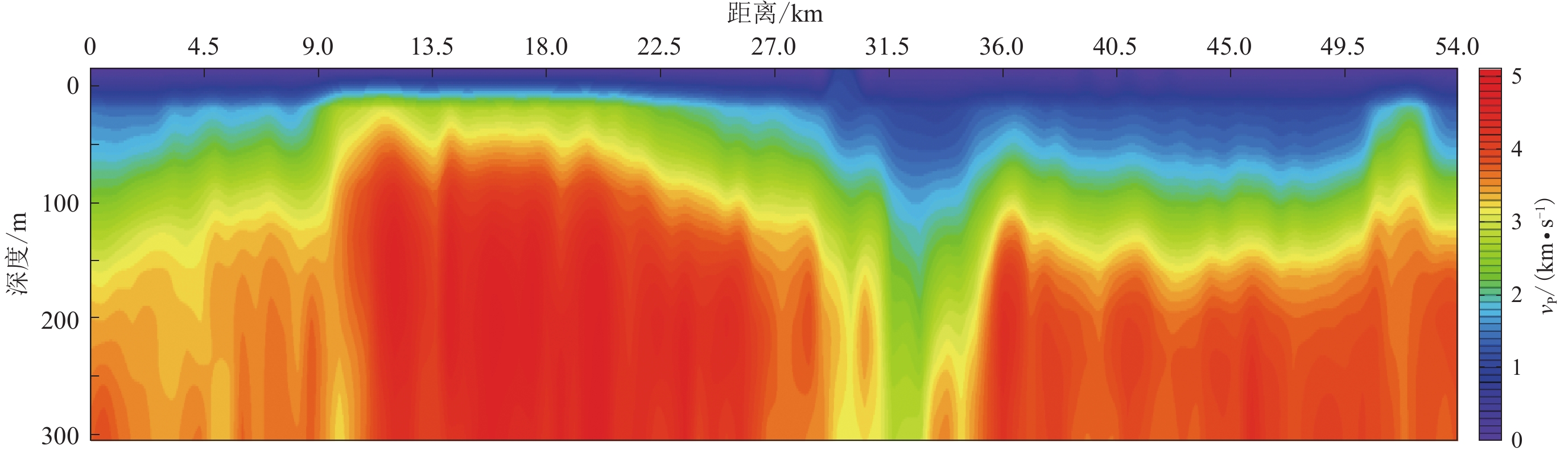
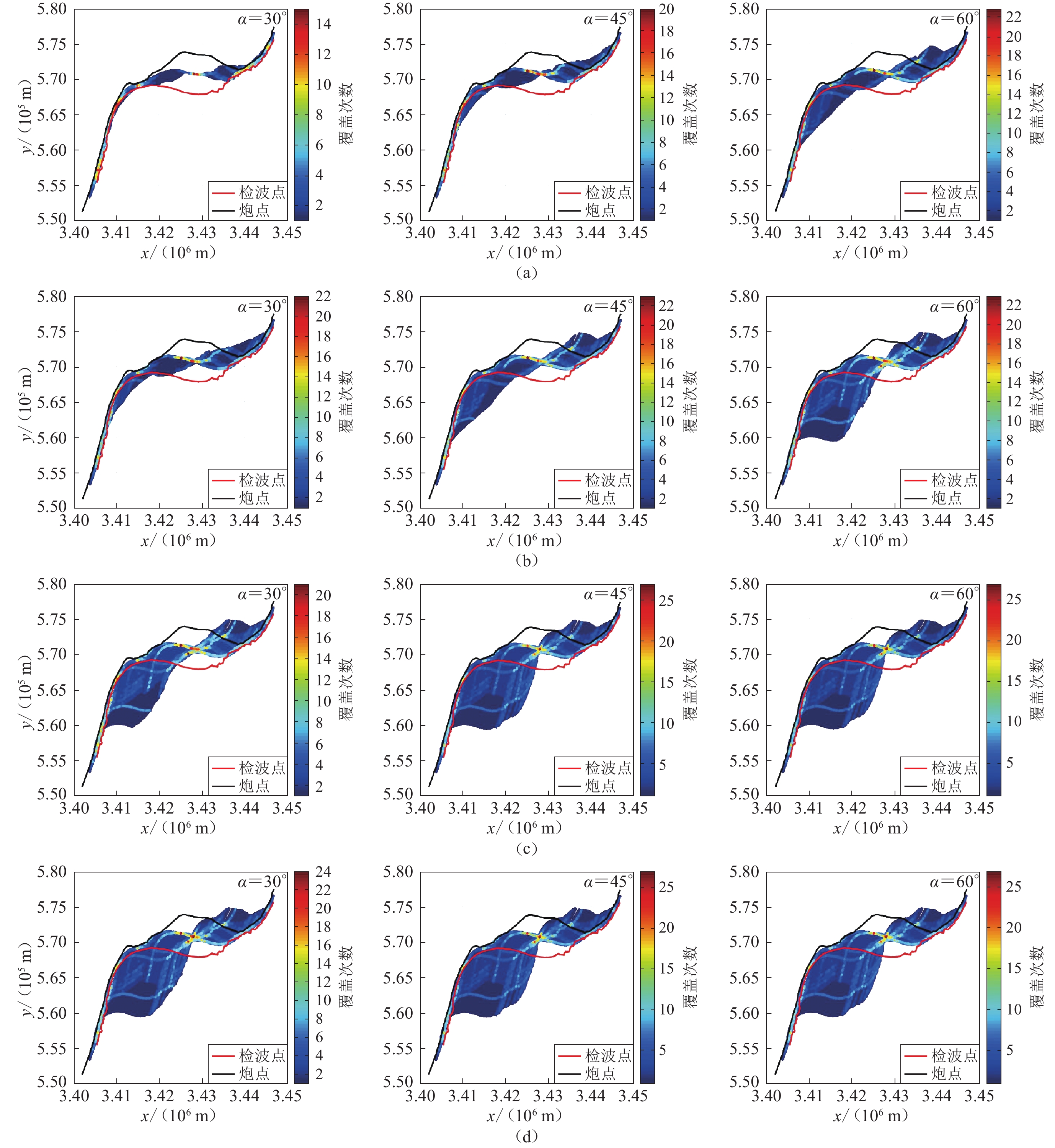
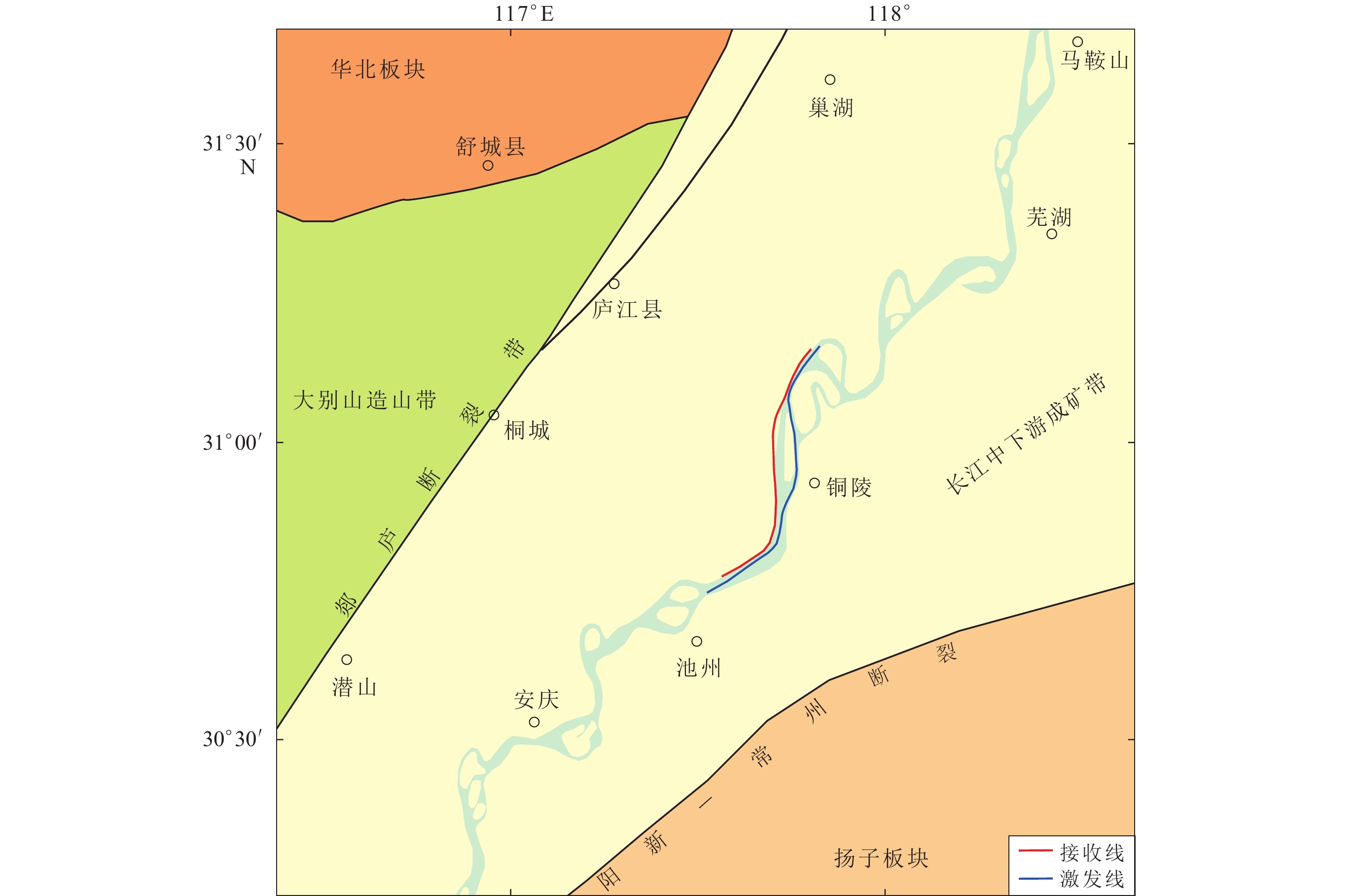
摘要: 为探索大容量气枪震源在深部地震探测中的应用，2015年10月在安徽铜陵段开展气枪流动激发试验。该试验采用沿长江航道激发、岸边固定排列接收的工作方式，因受长江航道及江岸地形的影响，加上原始记录中干扰波发育、静校正问题突出等，基于常规的共中心点叠加的数据处理方法已不再适用。为此，开展了针对性的数据处理方法研究。本文采用初至波层析静校正、叠前多域多道集去噪以及非纵弯线共反射面元叠加等一系列处理技术，结果显示所获测线经过区域的深部构造叠加剖面较清晰。Abstract: In order to explore the application of large-capacity airgun source in deep seismic reflection exploration, airgun flowing excitation experiment was carried out in the Tongling area of Anhui Province in October of 2015. The experiment adopts the working mode that the source is excited in Yangtze River channel and reflected signal is received in a fixed array along the shore. Due to the influence of the Yangtze River channel and river bank topography, coupled with development of interference wave and the prominent problem of static correction in the original records, the conventional processing method of common middle point superposition is no longer applicable in this region. Therefore, we carried out a targeted research on data processing methods. And a series of processing methods are applied, such as tomographic static correction, multi-domain and multi-channel joint de-noising and common reflection surface stacking of non-longitudinal bending line data. The results show that the obtained stacking section of deep structure is clear in the area where the survey line passes through. The results of this study can provide technical support and methodological reference for similar researches in other rivers using airgun source in the future.
-
引言
地震动合成广泛用于估计未来大地震产生的近场地震动。几十年来，多种理论和方法相继发展以用于合成地震动（Douglas，Aochi，2008）。常用的地震动合成方法可以分为数值方法、随机合成法、经验格林函数法、混合方法等。其中，数值方法受计算资源的限制，网格离散尺寸无法足够精细，难以保证合成地震动高频段的精度；随机合成的地震动在低频段又不够可靠。对于强震动观测记录的可靠频段和工程结构抗震分析所需地震动的低频、高频范围，宽频带（0.1—20 Hz）地震动成为当前的研究热点。目前，宽频带地震动合成常使用混合方法（Frankel，2009；Graves，Pitarka，2010），分别在低频段、高频段通过数值模拟、随机合成获得整个断层引起的地震动，再将两部分滤波、叠加得到宽频带地震动。其中，数值方法可以模拟三分量地震动，随机合成法只能提供一个无明确方位的水平分量，两种方法的叠加有不协调之处。此外，叠加所用交叉频率的选取具有主观性，两种方法对含义相同参数的表达也有不一致现象（孙晓丹，陶夏新，2012）。因此，需要研究计算精度高、逻辑严密的多分量宽频带地震动合成方法。
震源模型和格林函数是各种地震动合成方法的两个关键内容。Hartzell （1978）提出的有限断层震源模型广泛用于地震动合成，但震源描述形式各不相同。例如：经验格林函数法通过大震和小震的震源机制“调制”来表达震源（Irikura，Miyake，2011）；随机有限断层法用震源谱模型表达震源（Motazedian，Atkinson，2005）；包括本文方法在内的多种方法采用运动学震源模型，即，用有限断层面上的错动量分布、破裂速度、各子源时间函数和上升时间及滑动角等震源参数通过较为简单的数学表达描述颇为复杂的震源破裂过程。格林函数的计算是近场地震动合成的关键一环，也是不同地震动合成方法的核心区别。例如：经验格林函数法采用包含了真实场地效应和路径效应的小震（或余震）记录作为大震的格林函数（Irikura，Miyake，2011）；随机有限断层法用有限带宽白噪声描述随机格林函数（Motazedian，Atkinson，2005）。这些格林函数主要用于高频地震动合成，在低频段具有明显的偏差，且数值格林函数用于高频地震动合成时需要极大的计算资源（Graves，Pitarka，2010）。Wang （1999）、Zhu和Rivera （2002）等提出的格林函数算法解决了水平成层介质内源引起的三维位移响应问题，在地震动合成研究中受到关注（Hartzell et al，2005；Kieling et al，2014；Sun et al，2015）。这类地震动合成方法具有严密的理论基础，可以避免混合方法存在的逻辑缺陷，优势在于能够表达地壳介质内地震波的复杂传播过程，难点在于震源建模，有研究称之为基于物理的方法（physics-based）（Sun et al，2015）或基于震源的方法（source-based）（Hartzell et al，2011）。从工程应用的角度看，这类方法所用的水平成层地壳速度模型是与当前对地壳结构的认知水平相匹配的，既可以表达地壳的主要分层结构，也具有较高的计算效率。
基于频率波数域格林函数的地震动合成方法（frequency-wavenumber Green’s function，缩写为FK法）（Cao et al，2019），也属于这一类方法。曹泽林和陶夏新（2018）一文中指出，在地震动合成中，这类方法既有只用于低频段（Frankel，2009；Fortuño et al，2014），也有只用于高频段（Liu et al，2006），还有用于整个宽频带（Hartzell et al，2011；Sun et al，2015）。这一现状令人困惑，需要深入分析FK法的有效频带问题。本文借助一个算例，研究讨论FK法合成地震动的频带范围及其控制因素，重点考察三个方面的问题：① 频率波数域格林函数能不能传播宽频带地震波；② 震源模型有没有辐射出宽频带地震波；③ 这两者的控制要素有哪些。这一论证对FK法应用于工程场地的地震动合成、地震安全性评价是不可缺少的。
1. 合成地震动的FK法
1.1 FK法的计算原理
根据位移表示定理，点源引起的地表一点的地震动位移可以表示为（Aki，Richards，2002）
$$ {u_n}（{x}{\text{，}}t） {\text{＝}} {G_{np{\text{，}}q}}（{x}{\text{，}}t） * {M_{pq}}（t） {\text{，}} $$ (1) 式中：
${u_n}（{x}{\text{，}}t）$ 为点x的n方向位移；t为时间；*表示卷积；${G_{np{\text{，}}q}}（{x}{\text{，}}t）$ 为格林函数，表达单位强度的（p，q）方向力偶引起的点x的n方向位移；${M_{pq}}（t）$ 表示地震矩张量的分量，表达震源的作用。式（1）说明，地震动是由表达地壳介质传播特性的格林函数和表达震源破裂特征的地震矩张量卷积确定的，两部分的描述和计算构成不同类型地震动合成方法的基本框架。近断层地震动受震源破裂过程的显著控制，破裂面不能用点源描述，要采用Hartzell （1978）提出的有限断层震源模型。在有限断层震源模型中，整个破裂面划分为许多矩形小块，称之为子源并视作点源。各子源引起的地震动按一定的时滞叠加得到断层引起的地震动，即
$$ a（t） {\text{＝}} \sum\limits_{i {\text{＝}} 1}^{{N_{\rm{L}}}} {\sum\limits_{j {\text{＝}} 1}^{{N_{\rm{W}}}} {{a_{ij}}（t {\text{－}} \Delta {{t'_{ij}}} {\text{－}} \Delta {t''_{ij}}）} } {\text{，}} $$ (2) 式中，
$a（t）$ 为整个断层引起的地震动，${a_{ij}}（t）$ 为第ij个子源引起的地震动，$\Delta {t'_{ij}}$ 为第ij个子源的破裂时间，$\Delta {t''_{ij}}$ 为第ij个子源到地表点的传播时间，NL和NW分别为沿走向和沿断层面向下的子源数。对于FK法，第ij个子源引起的地震动可以表达为
$$ {a_{ij}}（t） {\text{＝}} {G_{ij}}（t） * {\rm{STF}}（{\tau _{ij}}{\text{，}}t）{M_{0ij}} {\text{，}} $$ (3) 式中，
${G_{ij}}（t）$ 为第ij个子源处单位冲激函数源引起的地表点的格林函数，${\rm{STF}}（{\tau _{ij}}{\text{，}}t）$ 为震源时间函数（简称STF），$ {\tau _{ij}} $ 和$ {M_{0ij}} $ 分别为第ij个子源的上升时间和地震矩。频率波数域格林函数的计算式为（Zhu，Rivera，2002；Kennett，2009）
$$ {\boldsymbol{G}}（r{\text{，}}\theta {\text{，}}{\textit{z}}{\text{，}}t） {\text{＝}} \frac{1}{{2\pi }}\sum\limits_{m {\text{＝}} 0{\text{，}}1{\text{，}}2} {\int_0^\infty {{{\text{e}}^{ - {\rm{i}}\omega t}}} {\rm{d}}\omega } \int_0^\infty {k{\rm{d}}k（{U_{\textit{z}}}{\boldsymbol{R}}_m^k {\text{＋}} {U_r}{\boldsymbol{S}}_m^k {\text{＋}} {U_\theta }{\boldsymbol{T}}_m^k）} {\text{，}} $$ (4) 式中，
$（r{\text{，}}\theta {\text{，}}{\textit{z}}）$ 为柱坐标系，$（{U_{\textit{z}}}{\text{，}}{U_r}{\text{，}}{U_\theta }）$ 为面谐矢量基$（{\boldsymbol{R}}_m^k{\text{，}}{\boldsymbol{S}}_m^k{\text{，}}{\boldsymbol{T}}_m^k）$ 的相应坐标，m为方位角模数，k为水平波数，ω为圆频率。由上述公式可知，FK法的基本要素包括格林函数
${G_{ij}}（t）$ 、描述各子源破裂过程的震源时间函数${\rm{STF}}（ \cdot ）$ 和上升时间$ {\tau _{ij}} $ 、子源地震矩$ {M_{0ij}} $ 、控制子源地震动叠加的$ \Delta {t'_{ij}} $ 和$ \Delta {t''_{ij}} $ 。1.2 本文采用的算例
为便于分析比较，本文采用图1所示的一个算例。首先，设定MW6.5直立走滑地震，断层长度和宽度分别为32 km和16 km，上缘埋深为5 km。整个断层面划分为16×8个2 km×2 km的子源。依据震源参数定标律（姜伟等，2017），平均错动量取为59 cm。有限断层震源模型的总地震矩为6.31×1018 N·m，由于采用均匀错动分布，每个子源的地震矩相等，均为4.93×1016 N·m。有限断层震源模型的一个子源的地震矩相当于一次MW5.1地震的地震矩。本文将图1所示子源视作点源，以便于后文分析。然后，设置距离断层中心地表投影30 km的基岩场地计算点A，用于地震动合成和比较分析。地壳速度结构模型采用四川芦山地区的模型（Hao et al，2013）（表1），原因在于该地区研究基础良好，地壳速度模型的浅处有厚度分别为3 km和5 km的两个薄层，便于分析地壳速度结构对破裂时间和传播时间的影响。
表 1 本文采用的地壳速度结构模型Table 1. Crustal velocity structure model adopted in this study厚度/km vP/（km·s−1） vS/（km·s−1） ρ/（g·cm−3） QP QS 3 4.88 2.86 2.55 300 150 5 5.80 3.40 2.70 400 200 14 6.04 3.55 2.75 400 200 21 6.82 3.98 2.90 600 300 25 7.61 4.45 3.10 800 400 - 8.08 4.47 3.38 1 000 500 1.3 FK法对地壳速度结构的表达
FK法采用的频率波数域格林函数表达了水平成层地壳模型的内源引起的响应，具体可参见相关文献（Zhu，Rivera，2002；Kennett，2009），本文不再赘述。除了格林函数，地壳速度结构还影响着震源参数。本小节讨论FK法中地壳速度结构对子源地震矩分配和两个时滞的影响。
在常用的地震动合成方法中，以子源的错动量为权将整个断层的地震矩分配给各子源，表达式为
$$ {M_{0ij}} {\text{＝}} \frac{{{M_0}{D_{ij}}}}{{\displaystyle\sum\limits_{i{\text{＝}}1}^{{N_{\rm{L}}}} {\displaystyle\sum\limits_{j{\text{＝}}1}^{{N_{\rm{W}}}} {{D_{ij}}} } }} {\text{，}} $$ (5) 式中，M0为整个断层的地震矩，Dij为第ij个子源的错动量。
FK法考虑了子源地震矩与子源的剪切模量
$ {\mu _{ij}} $ 、错动量$ {D_{ij}} $ 、面积A的关系${M_{0ij}} {\text{＝}} {\mu _{ij}}A{D_{ij}}$ ，可以更合理地加权分配各子源地震矩，即$$ {M_{0ij}} {\text{＝}} \frac{{{M_0}{\mu _{ij}}{D_{ij}}}}{{\displaystyle\sum\limits_{i{\text{＝}}1}^{{N_{\rm{L}}}} {\displaystyle\sum\limits_{j{\text{＝}}1}^{{N_{\rm{W}}}} {{\mu _{ij}}{D_{ij}}} } }}{\text{.}} $$ (6) 式（2）中的破裂时间表达子源破裂的触发时刻，一般由破裂起始点到子源的距离除以破裂速度得到，即
$$ \Delta {t'_{ij}} {\text{＝}} \frac{{{L_{ij}}}}{{{v_{\rm{r}}}}}{\text{，}}$$ (7) 式中，Lij为破裂起始点到第ij个子源的距离，vr为破裂速度。破裂速度常按下式确定
$$ {v_{\rm{r}}} {\text{＝}} \beta {v_{\rm{S}}} {\text{，}} $$ (8) 式中，β为破裂速度与剪切波速vS的比值，常取为0.8。
地壳介质剪切波速通常随深度变化，对破裂速度的分布和各子源的破裂时间有一定的影响。对于表1的地壳速度模型和图1的震源模型（此时断层埋深另取为0 km，以突出近地表波速复杂变化的影响），采用同一破裂速度2.7 km/s和深度相关破裂速度，计算得到的破裂时间的分布如图2所示。由图可见，考虑地壳介质剪切波速变化时，浅部破裂时间变大，深部破裂时间变小，差值最大达到0.5 s。这说明有必要考虑地壳结构对破裂速度的影响。
![]()
图 2 不同破裂速度计算的破裂时间。星号表示破裂起始点（a） 同一破裂速度；（b） 深度相关破裂速度；（c） 深度相关破裂速度的分布；（d） 图（b）相对图（a）的差值Figure 2. Rupture time calculated by different rupture velocity vr（a） The same vr ；（b） Depth-related vr；（c） Distribution of depth-related vr； （d） Difference between Fig.（b） and Fig.（a）式（2）中的传播时间一般由子源到地表点的距离除以剪切波速得到，即
$$ \Delta {t''_{ij}} {\text{＝}}\frac{ {{R_{ij}}} }{{v_{\rm{S}}}} {\text{，}} $$ (9) 式中，Rij为第ij个子源到地表点的距离。
地壳介质中的剪切波速随深度发生变化，这会影响地震波传播速度，影响特点需要仔细分析。将震源设置于不同深度，对于不同震中距的地表点，采用同一剪切波速3.4 km/s和表1中的深度相关剪切波速计算S波的传播时间，结果如图3所示。由图可见，对于深度相关剪切波速，传播时间的等值线有多处转折且浅部和深部的增加趋势不同。图中的粗折线是两类初至波的分界线，左侧是震源向上传播的直达波先到达地表，右侧是震源向下传播的体波反射波先到达地表，粗折线水平段的位置正好对应地壳结构中速度不连续界面的深度，说明了地壳结构对传播时间的重要影响。考虑地壳介质剪切波速变化时，浅部传播时间变大，深部传播时间变小，差距最大达到3 s。考虑地壳结构对传播时间的影响也是有必要的，这对于FK法合成地震动的可靠性和有效频带具有重要意义。
![]()
图 3 不同剪切波速计算的S波的传播时间（a） 同一剪切波速；（b） 深度相关剪切波速；（c） 图（b） 相对图 （a） 的差值Figure 3. Propagation time of S wave calculated by different$v_{\rm{S}} $ （a） The same $v_{\rm{S}} $；（b） Depth-related $v_{\rm{S}} $；（c） Difference between Fig.（b） and Fig.（a）2. 格林函数计算的影响
考察式（4）可知，格林函数的计算式是严谨的解析表达式，对频率、波数的积分域均是从0到无穷。在实际数值计算中，频率和波数均截止到某最大值，因此FK法被称为一种半解析方法。本节分析频率和波数积分范围的截断处理对地震波计算的影响，并考察频率波数域格林函数是否能传播宽频带地震波。
2.1 关于频率的积分
一个离散的时程能够表达的最高频率称为奈奎斯特（Nyquist）频率。根据采样定理，奈奎斯特频率fN由下式确定，即
$$ {f_N} {\text{＝}} \frac{1}{{2{\rm{d}}t}} {\text{，}} $$ (10) 相应的频率离散间隔df为
$$ {\rm{d}}f = \frac{1}{T} {\text{＝}} \frac{1}{{{N_t}{\rm{d}}t}} {\text{，}}$$ (11) 式中，T为总时长，dt为时间步距，Nt为时间步距的总数。
在式（4）中，截止圆频率ωN和圆频率离散间隔dω分别为
$$ {\omega _N} {\text{＝}} 2\pi {f_N}{\text{ = }}\frac{\pi }{{{\rm{d}}t}} {\text{，}} $$ (12) $$ {\rm{d}}\omega {\text{＝}} 2\pi {\rm{d}}f {\text{＝}} \frac{{2\pi }}{{{N_t}{\rm{d}}t}} {\text{.}} $$ (13) 在格林函数计算中，Nt和dt的取值要考虑震源至地表点的距离范围和地表点的地震动持时，也要保证fN和df都满足宽频带计算的要求。在FK法中，子源格林函数的零时刻是子源破裂的起始时刻。一般情况下，格林函数的总时长T都大于20 s。根据式（11），df小于0.05 Hz，完全能够表达格林函数的谱幅值随频率的复杂变化。
根据式（10），时间步距dt确定了格林函数能表达的最高频率，对FK法合成地震动的频带具有显著影响。下面分析fN对合成地震动频带的影响。取Nt为4 096，dt为0.01，0.02，0.05，0.1，0.5 s，对应的fN为50，25，10，5，1 Hz。采用图1中的点源，分别计算相应的格林函数，然后合成点A的断层垂直（fault normal，缩写为FN）分量的地震动。不同fN合成地震动的加速度幅值谱（Fourier amplitude spectrum，缩写为FAS）的比较如图4所示。图中，左侧是上升时间为0 s的结果，表达单位冲激函数源的影响；右侧是上升时间为1.5 s的结果，表达考虑震源破裂过程的影响。为了更直观地表达合成地震动的频谱特征，本文采用了Konno和Ohmachi （1998）的方法对幅值谱进行了光滑处理。由图4可见，频率波数域格林函数可以表达fN以下的频率成分。当dt足够小，fN足够大时，格林函数能够传播宽频带地震波。在接近于fN时，格林函数一定程度偏小，这是由于数值计算的精度损失。对于0.1 Hz以下的频段，fN较小的结果有一定的偏差，这是由于dt较大时，计算精度较差。对比图4a和4b，震源破裂过程的时长（即上升时间）影响合成地震动的谱幅值水平，但在可靠的频率范围内没有中间频段缺失现象。dt除了确定格林函数的最高频率，还影响FK法的计算量。表2说明不同dt时FK法合成地震动的计算量。可见，当dt从0.02 s变为0.01 s时，地震动合成的计算时间和数据存储空间都变为原来的2倍（本文计算所用的台式计算机配置为CPU i5-10400、运行内存16 G）。对于本文算例，计算量差别不大。但对于汶川MW7.9地震之类的大地震，除了距离范围大，断层面也需要划分为更多的子源，此时计算量的差异就十分显著了。因此，考虑到数值计算效率，dt取0.02 s，可以满足宽频带地震动合成的需要。
![]()
图 4 上升时间为0 s （a）和1.5 s （b） 时奈奎斯特频率对合成地震动加速度幅值谱FAS的影响Figure 4. Influence of Nyquist frequency on FAS of synthetic ground motion with rise time of 0 s （a） and 1.5 s （b）表 2 不同dt时FK法合成地震动的计算量Table 2. Calculation cost of ground motion simulation using FK approach for different dt算例 子源数 dt/s 地表某点地震动的
计算耗时/s地震动场（网格2×2 km2） 耗时/h 存储空间/GB 范围/km2 本文算例
MW6.516×8 0.02 1.4 0.7 0.23 100×70 16×8 0.01 2.8 1.4 0.46 100×70 汶川地震
MW7.964×32 0.02 22.4 126.3 2.56 400×200 64×32 0.01 44.8 252.6 5.12 400×200 2.2 关于波数的积分
FK法的格林函数在波数域求解震源引起的响应，很好地解决了数值稳定问题（Zhu，Rivera，2002）。式（4）中关于波数的积分，数值计算截止到最大波数。零频最大波数kmax和波数间隔dk是提前设定的。理论上讲，kmax越大、dk越小，越有利于格林函数的计算精度，但dk变小时计算量会显著增加。以表1中的地壳速度结构模型为例，表3说明了不同dt、dk和kmax时FK法格林函数的计算量。当dt从0.02 s变为0.01 s时，格林函数计算时间和数据存储空间分别为原来的4倍和2倍。下面分析kmax和dk对合成地震动频带和计算量的影响，除了确定参数的建议值，还可以了解参数的合理取值范围。
表 3 不同dt，dk和kmax时FK法格林函数的计算量Table 3. Calculation cost of Green’s function in FK approach with different dt, dk and kmaxdt/s dk kmax 计算耗时（源深6 km）/s 150个地表点60组（源深差0.5 km） 30 km处一点 150个地表点 耗时/h 存储空间/GB 0.02 0.1 15 8 239 3.98 3.09 0.01 0.1 15 34 954 15.90 6.18 0.02 0.05 15 17 483 8.05 3.09 0.02 0.3 15 3 81 1.35 3.09 0.02 0.1 5 8 236 3.93 3.09 0.02 0.1 20 8 240 4.00 3.09 注：150个地表点的震中距设为1，2，···，150 km kmax和dk的单位是1/Xmax，Xmax是点源埋深与点源至地表点的震中距两者中的较大值。对于图1中的点源，Xmax为30 km。取dk为0.1，kmax取为2，5，10，15，20，分别计算相应的格林函数，然后合成点A的FN分量地震动。不同kmax合成地震动的FAS和位移时程的比较如图5a所示。从图中可见，kmax过小时，0.1 Hz以下和接近fN的频段的FAS有一定偏差，其它频率的差距不明显。kmax越大，位移计算结果越精确。kmax对格林函数计算量的影响小，主要影响计算精度与稳定性。kmax取为10以上时可满足计算精度要求，为避免特殊问题，本文建议kmax取为15。
![]()
图 5 最大波数（a）和波数间隔（b）对合成地震动加速度幅值谱FAS和位移时程的影响Figure 5. Influence of the maximum wavenumber （a） and the wavenumber interval （b） on FAS and displacement time history of synthetic ground motion取kmax为15，dk分别取为0.05，0.1，0.2，0.3，0.5。采用图1中的点源，分别计算相应的格林函数，然后合成点A的FN分量地震动。不同dk合成地震动的FAS和位移时程的比较如图5b所示。从图中可见，对于1 Hz以下频段，dk较大时，合成地震动的偏差随频率减低而增加；在1—10 Hz频段，dk的影响很小。从fN以上频段的FAS可以发现，FAS受dk的显著影响并不是单调变化的，这是因为在式（4）中，关于波数的积分因子随波数有明显的振荡现象，dk从小变大时，积分点并非单调变化。dk应足够小，以保证能够描述积分因子随波数的复杂变化，dk大于0.2时，位移时程出现计算错误及失稳现象。表3说明，当dk从0.1变为0.05，0.3时，格林函数的计算时间分别为原来的2倍和0.33倍。对于汶川MW7.9地震之类的大地震，格林函数的计算量差距会十分显著。考虑到计算精度和计算效率，本文建议dk取为0.1，更高要求时可取为0.05。
2.3 地壳速度结构影响一例
地壳速度结构对格林函数的幅值、波形具有控制作用。在地壳速度结构中，品质因子是描述地壳介质耗能衰减的参数。下面以品质因子为例，分析其对格林函数频带的影响特点。对于表1的地壳速度结构模型，分别将品质因子取为原值的0.5，1.0，2.0倍。采用图1中的点源，分别计算相应的格林函数，然后合成点A的FN分量地震动。不同品质因子合成地震动的FAS的比较如图6所示。由图可见，品质因子主要影响1 Hz以上的高频地震动，影响程度随频率增加。这一分析表明，地壳结构影响不同频段谱幅值的总体水平，但不影响FK法合成地震动可靠的频带宽度。
![]()
图 6 品质因子对合成地震动加速度幅值谱FAS的影响Figure 6. Influence of quality factor on FAS of synthetic ground motion3. 震源破裂过程的影响
根据式（3），为了表达震源破裂过程释放地震矩需要一定时间、地震矩释放速率随时间的变化，地震动合成需要卷积格林函数与震源时间函数。震源时间函数（STF）描述地震矩率（或错动速率）的时间历程，目前，还很难对每一个子源都估计一个不同的震源时间函数。一般做法是采用相同的函数形式，对每一个子源估计各不相同的上升时间和地震矩。此外，破裂速度控制各子源破裂触发时间，也是一个重要参数。本节讨论震源时间函数、上升时间、破裂速度对合成地震动频带的影响，考察标准主要包括两方面：合成地震动的频带宽度是否覆盖0.1—20 Hz；在整个宽频带范围内，这些参数（或模型）是否会造成某些频段地震动幅值过小或过大。
3.1 震源时间函数的影响
迄今为止，地震反演和正演研究中已经有多种STF解析函数表达式，包括简单的数学函数和具有震源动力学含义的函数。根据来源和函数形式，震源时间函数可以分为简单类型、三角函数类型、Brune类型和Yoffe类型。本文参考前期研究（Cao et al，2019），选取三角形STF、Liu STF （Liu et al，2006）、Hartzell STF （Hartzell et al，2007）、Brune STF （Brune，1970）和三角形规则化的Yoffe STF （Tinti et al，2005）等五种典型模型，分析震源时间函数对合成地震动频带的影响。图7比较了五种模型表达的错动速率及其幅值谱。采用图1中的点源，分别合成点A的FN分量地震动。图8比较了五种震源时间函数模型合成地震动的幅值谱。其中，幅值比较是以具有f−2高频谱衰减速率的Brune STF的结果为参考值。
![]()
图 7 五种震源时间函数的错动速率（a）及其加速度幅值谱FAS （b）Figure 7. Slip rate （a） and its FAS （b） for five source time functions![]()
图 8 震源时间函数对合成地震动加速度幅值谱FAS的影响Figure 8. Influence of source time function on FAS of synthetic ground motion一般来讲，STF的函数形式对散射地震波的表达存在几方面问题（Dreger et al，2007），包括错动速率的对称性、错动速率FAS中间频段幅值很小的谱洞、谱高频衰减速率，一般从这几方面分析震源时间函数的模型及其影响。在震源破裂过程中，错动速率通常先快速增加到最大值然后逐渐变小（Day，1982）。这说明STF的错动速率随时间的变化不是对称的，STF的错动速率应在错动早期具有一个有限的峰值。这描述了震源破裂过程释放能量随时间的变化，主要影响合成地震动的波形。STF的幅值谱中较大的振荡称为谱洞，会导致频率相关地震动参数出现较大偏差。例如，三角形STF合成地震动的FAS在1 Hz和2 Hz处有明显低估，Yoffe STF使相应FAS在3 Hz处亦有明显低估，正好对应STF的FAS的谱洞位置。震源破裂过程释放地震波的谱幅值随频率的变化应当是连续的，不应有剧烈振荡。因此，无谱洞的STF更适用于描述震源破裂过程和地震动合成。此外，STF应具有f-2高频谱衰减速率，衰减过快或过慢会低估或高估地震动，都不利于合成宽频带地震动，例如，Liu STF在中频段明显较大的幅值会高估这个频段的地震动。由式（3）可知，对于FK法的震源模型，上升时间含义明确的Hartzell STF比Brune STF更适用于描述子源错动的时间变化，也是本文推荐的最优模型。
3.2 上升时间的影响
上升时间表征破裂面上一点从破裂开始直至最终达到静态位错所历经的时间。根据相关研究（Brune，1970；Beresnev，2002），上升时间的频域等效参数是震源谱模型中的拐角频率。对于Hartzell STF，上升时间分别取为0，0.5，1.0，2.0，5.0 s，表示震源错动时间变化对合成地震动频带的影响。采用图1中的点源，分别合成点A的FN分量地震动。不同上升时间合成地震动的FAS的比较如图9a所示。从图中可见，上升时间是控制地震动幅值的最重要因素，比格林函数的控制作用要大很多。随着上升时间的增大，地震动谱幅值显著降低。这说明描述错动速率的上升时间控制了震源破裂释放高频地震波的能量，错动越快释放的高频地震动越强。结合图4和图9可知，上升时间显著影响合成地震动的谱幅值水平，但在可靠的频率范围内没有中间频段缺失现象。
![]()
图 9 上升时间（a）和破裂速度（b）对合成地震动加速度幅值谱FAS的影响Figure 9. Influence of rise time （a） and rupture velocity （b） on FAS of synthetic ground motion3.3 破裂速度的影响
根据式（2），震源时间函数和上升时间描述一个子源的错动过程，各子源的错动过程按一定时滞叠加组成整个震源破裂面的破裂过程。下面研究子源叠加是否影响合成地震动的频带。为此，分别将破裂速度取为剪切波速的0.6，0.7，0.8，0.9，1.0倍，计算破裂速度和破裂时间。采用Hartzell STF和1.5 s上升时间，采用图1中的整个有限断层震源模型，合成点A的FN分量地震动。不同破裂速度合成地震动的FAS的比较，如图9b所示。从图中可见，在0.1—0.5 Hz范围内，FAS随破裂速度增加。这与预期相符，原因在于破裂速度越大，各子源地震动的时滞越小，合成地震动越强。在1 Hz以上高频段，破裂速度对FAS的影响不显著。在0.5—1.0 Hz范围内，破裂速度的影响规律与低频段相反，分析发现，这是由于图1中均匀错动分布引起的有限断层模型人为周期性。对于不均匀错动分布，人为周期性会大大减小。在实际地震动合成中，破裂速度对合成地震动可靠的频带宽度的影响较小。
4. 讨论与结论
FK法是基于有限断层震源模型的地震动合成方法，采用频率波数域格林函数表达地震波在地壳介质内的复杂传播过程，采用震源时间函数和上升时间描述子源的破裂过程，具有严密的理论基础。FK法充分表达了地壳速度结构对格林函数、子源地震矩、破裂时间和传播时间的影响，更符合地震波传播规律。格林函数的计算分析表明，FK法的格林函数具有表达宽频带地震波传播的能力。在计算格林函数时，时间步距、波数间隔以及零频最大波数应取值合理，以保证合成地震动的频带宽度、计算精度和计算效率，本文建议dt取0.02 s、dk取0.1、kmax取15、Nt按需取值。本文以品质因子为例，分析了地壳速度结构对合成地震动频带的影响。研究表明，地壳结构影响地震动谱幅值的总体水平，但可靠的频带宽度不变。震源破裂过程的影响研究表明，FK法的震源破裂过程能够辐射宽频带地震波，这需要选取合适的震源时间函数、对上升时间和破裂速度进行合理约束。震源时间函数对震源辐射地震波的频谱成分具有控制性作用，应满足错动速率对称性、谱洞、谱衰减速率等方面的要求，本文建议选用Hartzell STF描述子源错动过程。上升时间和破裂速度影响合成地震动的谱幅值的总体水平，在可靠的频率范围内没有中间频段缺失现象。子源地震动的叠加应注意避免人为周期性的影响。总之，在合理约束震源上升时间和破裂速度、选用震源时间函数和地壳速度结构模型时，FK法合成地震动能够表达宽频带范围，在多分量宽频带地震动合成中有良好的应用前景。
-
![]()
图 1 安徽铜陵气枪试验测线位置图
Figure 1. Location of seismic lines of airgun experiment in Tongling，Auhui Province
![]()
图 2 应用层析静校正前（a）、后（b）的单炮记录对比图
Figure 2. Comparison of shot records before （a） and after （b） tomography static correction
![]()
图 3 沿面元中心线的近地表P波速度结构
Figure 3. Near surface P-wave velocity structure along midpoint line of common center bins
![]()
图 4 多域多道集联合去噪前（a）、后（b）的单炮记录对比图
Figure 4. Comparison of shot records before （a） and after （b） multi-domain and multi-channel de-noising
![]()
图 5 不同深度h上不同反射角α的面元分布及覆盖次数图
Figure 5. Distribution of bins and folds with different depths h and reflection angles α
（a） h＝5 km；（b） h＝10 km；（c） h＝25 km；（d） h＝35 km
表 1 去噪方法和参数
Table 1 De-noising methods and related parameters
处理方法 处理参数 时变带通滤波 0—6 s （8—40 Hz）；6—8 s （6—30 Hz）；
8—30 s （4—25 Hz）自适应面波压制 频率范围为0—6 Hz，给定速度500 m/s f-x频率域随机
噪声衰减横向道数151，时窗500 ms，增益窗口1 000 ms 
下载: 导出CSV
-
常印佛, 刘湘培, 吴言昌. 1991. 长江中下游铜铁成矿带[M]. 北京: 地质出版社: 1–239. Chang Y F, Liu X P, Wu Y C. 1991. The Copper-Iron Belt of the Lower and Middle Reaches of the Changjiang River[M]. Beijing: Geological Publishing House: 1–239 （in Chinese）.
常印佛,董树文,黄德志. 1996. 论中—下扬子“一盖多底”格局与演化[J]. 火山地质与矿产,17(1/2):1–15. Chang Y F,Dong S W,Huang D Z. 1996. On tectonics of “poly-basement with one cover” in middle-lower Yangtze craton China[J]. Volcanology &Mineral Resources,17(1/2):1–15 (in Chinese).
陈安国,周涛发,刘东甲,葛粲. 2017. 长江中下游成矿带及邻区Moho深度与成矿背景探讨[J]. 地质学报,91(6):1299–1311. doi: 10.3969/j.issn.0001-5717.2017.06.010 Chen A G,Zhou T F,Liu D J,Ge C. 2017. The Moho depth and metallogenic setting of the middle-lower Yangtze River valley metallogenic belt and its adjacent areas[J]. Acta Geologica Sinica,91(6):1299–1311 (in Chinese).
陈佳,李孝宾,杨军,叶泵. 2016. 云南宾川大容量气枪震源波形频谱特征分析[J]. 中国地震,32(2):216–221. doi: 10.3969/j.issn.1001-4683.2016.02.007 Chen J,Li X B,Yang J,Ye B. 2016. Large volume air-gun source spectrum characteristics of Binchuan,Yunnan[J]. Earthquake Research in China,32(2):216–221 (in Chinese).
陈颙,李宜晋. 2007. 地震波雷达研究展望:用人工震源探测大陆地壳结构[J]. 中国科学技术大学学报,37(8):813–819. doi: 10.3969/j.issn.0253-2778.2007.08.002 Chen Y,Li Y J. 2007. Seismic wave radar research:Using active source to detect continental crust structure[J]. Journal of University of Science and Technology of China,37(8):813–819 (in Chinese).
陈颙,王宝善,姚华建. 2017. 大陆地壳结构的气枪震源探测及其应用[J]. 中国科学:地球科学,47(10):1153–1165. Chen Y,Wang B S,Yao H J. 2017. Seismic airgun exploration of continental crust structures[J]. Science China Earth Sciences,60(10):1739–1751. doi: 10.1007/s11430-016-9096-6
酆少英,刘保金,秦晶晶,姬计法,王宏伟,魏学强,李稳,谭雅丽. 2020. 大容量气枪震源陆地反射地震探测:以长江中下游铜陵地区为例[J]. 中国地震,36(2):200–210. Feng S Y,Liu B J,Qin J J,Ji J F,Wang H W,Wei X Q,Li W,Tan Y L. 2020. The seismic reflection survey using large capacity air-gun source:A case study of Tongling area in mid-lower reaches of the Yangtze river[J]. Earthquake Research in China,36(2):200–210 (in Chinese).
兰学毅,杜建国,严加永,安明,万秋,郭冬,廖梦奇,王云云,陶龙,张启燕,张莎莎. 2015. 基于先验信息约束的重磁三维交互反演建模技术:以铜陵矿集区为例[J]. 地球物理学报,58(12):4436–4449. doi: 10.6038/cjg20151209 Lan X Y,Du J G,Yan J Y,An M,Wan Q,Guo D,Liao M Q,Wang Y Y,Tao L,Zhang Q Y,Zhang S S. 2015. 3D gravity and magnetic interactive inversion modeling based on prior information:A case study of the Tongling ore concentration area[J]. Chinese Journal of Geophysics,58(12):4436–4449 (in Chinese).
林建民,王宝善,葛洪魁,唐杰,张先康,陈颙. 2008. 大容量气枪震源特征及地震波传播的震相分析[J]. 地球物理学报,51(1):206–212. doi: 10.3321/j.issn:0001-5733.2008.01.025 Lin J M,Wang B S,Ge H K,Tang J,Zhang X K,Chen Y. 2008. Study on large volume airgun source characteristics and seismic phase analysis[J]. Chinese Journal of Geophysics,51(1):206–212 (in Chinese).
刘建芳,郭赟,鲍伟,管文华. 2007. 复杂地表二维弯曲测线地震资料处理方法研究[J]. 石油物探,46(2):196–201. doi: 10.3969/j.issn.1000-1441.2007.02.019 Liu J F,Guo Y,Bao W,Guan W H. 2007. Research on 2-D seismic data processing slalom lines in complex surface condition[J]. Geophysical Prospecting for Petroleum,46(2):196–201 (in Chinese).
吕庆田,董树文,史大年,汤井田,江国明,张永谦,徐涛,SinoProbe-03-CJ项目组. 2014. 长江中下游成矿带岩石圈结构与成矿动力学模型:深部探测(SinoProbe)综述[J]. 岩石学报,30(4):889–906. Lü Q T,Dong S W,Shi D N,Tang J T,Jiang G M,Zhang Y Q,Xu T,SinoProbe-03-CJ Group. 2014. Lithosphere architecture and geodynamic model of middle and lower reaches of Yangtze metallogenic belt:A review from SinoProbe[J]. Acta Petrologica Sinica,30(4):889–906 (in Chinese).
丘学林,陈颙,朱日祥,徐辉龙,施小斌,叶春明,赵明辉,夏少红. 2007. 大容量气枪震源在海陆联测中的应用:南海北部试验结果分析[J]. 科学通报,52(4):463–469. doi: 10.3321/j.issn:0023-074X.2007.04.015 Qiu X L,Chen Y,Zhu R X,Xu H L,Shi X B,Ye C M,Zhao M H,Xia S H. 2007. The application of large volume airgun sources to the onshore-offshore seismic surveys:Implication from the experimental results in northern South China Sea[J]. Chinese Science Bulletin,52(4):533–560.
孙涛,李杭,吴开兴,陈陵康,刘卫明,胡紫娟. 2018. 铜陵矿集区断裂分形与多重分形特征[J]. 有色金属工程,8(4):111–115. doi: 10.3969/j.issn.2095-1744.2018.04.022 Sun T,Li H,Wu K X,Chen L K,Liu W M,Hu Z J. 2018. Fractal and multifractal characteristics of regional fractures in Tongling metallogenic area[J]. Nonferrous Metals Engineering,8(4):111–115 (in Chinese).
唐杰,王宝善,葛洪魁,陈颙. 2009. 大容量气枪震源的实验与模拟研究[J]. 中国地震,25(1):1–10. doi: 10.3969/j.issn.1001-4683.2009.01.001 Tang J,Wang B S,Ge H K,Chen Y. 2009. Study of experiment and simulation of large volume air-gun in deep structures exploration[J]. Earthquake Research in China,25(1):1–10 (in Chinese).
汤井田,周聪,任政勇,王显莹,肖晓,吕庆田. 2014. 安徽铜陵矿集区大地电磁数据三维反演及其构造格局[J]. 地质学报,88(4):598–611. Tang J T,Zhou C,Ren Z Y,Wang X Y,Xiao X,Lü Q T. 2014. Three dimensional magnetotelluric inversion and structural framework of Tongling ore district,Anhui[J]. Acta Geologica Sinica,88(4):598–611 (in Chinese).
田晓峰,王夫运,刘宝峰,杨卓欣,郑成龙,高占永. 2016. 马鞍山—铜陵—安庆长江沿线上地壳速度结构成像[J]. 中国地震,32(2):390–396. doi: 10.3969/j.issn.1001-4683.2016.02.022 Tian X F,Wang F Y,Liu B F,Yang Z X,Zheng C L,Gao Z Y. 2016. Upper crustal velocity structure along the Yangtze River from Ma’anshan to Anqing[J]. Earthquake Research in China,32(2):390–396 (in Chinese).
汪铁望,于相海,胡浩,刘明乾,周夏丽. 2010. 弯曲测线地震资料相干噪声压制[J]. 地球物理学进展,25(3):946–950. doi: 10.3969/j.issn.1004-2903.2010.03.031 Wang T W,Yu X H,Hu H,Liu M Q,Zhou X L. 2010. Attenuation of coherent noise in seismic data coith crooked line geometry[J]. Progress in Geophysics,25(3):946–950 (in Chinese).
魏斌,苏金波,王海涛,郑黎明,王琼,张文来,袁顺,魏芸芸,陈昊. 2016. 新疆呼图壁人工水体大容量气枪信号发射台性能研究[J]. 中国地震,32(2):222–230. doi: 10.3969/j.issn.1001-4683.2016.02.008 Wei B,Su J B,Wang H T,Zheng L M,Wang Q,Zhang W L,Yuan S,Wei Y Y,Chen H. 2016. Site selection and construction of Hutubi airgun source signal transmitting seismic station and its characteristic of source[J]. Earthquake Research in China,32(2):222–230 (in Chinese).
吴言昌,曹奋扬,常印佛. 1999. 初论安徽沿江地区成矿系统的深部构造:岩浆控制[J]. 地学前缘,6(2):285–296. doi: 10.3321/j.issn:1005-2321.1999.02.007 Wu Y C,Cao F Y,Chang Y F. 1999. A preliminary study on the deep seated structural magmatic control over the metallogenic system around the Yangtze river reaches in Anhui Province[J]. Earth Science Frontiers,6(2):285–296 (in Chinese).
杨庆道,王伟锋,尹以东,赵玉生,李继白. 2011. 弯线地震勘探技术应用中的若干问题[J]. 石油地球物理勘探,46(3):364–369. Yang Q D,Wang W F,Yin Y D,Zhao Y S,Li J B. 2010. Some issues in applications of seismic crooked line[J]. Oil Geophysical Prospecting,46(3):364–369 (in Chinese).
赵明辉,丘学林,叶春明,夏戡原,黄慈流,谢剑波,王平. 2004. 南海东北部海陆深地震联测与滨海断裂带两侧地壳结构分析[J]. 地球物理学报,47(5):845–852. doi: 10.3321/j.issn:0001-5733.2004.05.016 Zhao M H,Qiu X L,Ye C M,Xia K Y,Huang C L,Xie J B,Wang P. 2004. Analysis on deep crustal structure along the onshore-offshore seismic profile across the Binhai (Littoral) fault zone in northeastern South China Sea[J]. Chinese Journal of Geophysics,47(5):845–852 (in Chinese).
周涛发,范裕,袁峰. 2008. 长江中下游成矿带成岩成矿作用研究进展[J]. 岩石学报,24(8):1665–1678. Zhou T F,Fan Y,Yuan F. 2008. Advances on petrogensis and metallogeny study of the mineralization belt of the middle and lower reaches of the Yangtze river area[J]. Acta Petrologica Sinica,24(8):1665–1678 (in Chinese).
Brocher T M, Clayton R W, Klitgord K D, Bohannon R G, Sliter R, McRaney J K, Gardner J V, Keene J B. 1995. Multichannel Seismic-Reflection Profiling on the R/V Maurice Ewing During the Los Angeles Region Seismic Experiment （LARSE）, California[R]. U.S. Geological Survey Open-File Report: USGS-OFR-95-228.
Okaya D,Henrys S,Stern T. 2002. Double-sided onshore-offshore seismic imaging of a plate boundary: “Super-gathers” across South Island,New Zealand[J]. Tectonophysics,355(1/2/3/4):247–263.
She Y Y,Yao H J,Zhai Q S,Wang F Y,Tian X F. 2018. Shallow crustal structure of the middle-lower Yangtze River region in eastern China from surface-wave tomography of a large volume airgun-shot experiment[J]. Seismol Res Lett,89(3):1003–1013. doi: 10.1785/0220170232
Tian X F,Yang Z X,Wang B S,Yao H J,Wang F Y,Liu B F,Zheng C L,Gao Z Y,Xiong W,Deng X G. 2018. 3D seismic refraction travel-time tomography beneath the middle-lower Yangtze River region[J]. Seismol Res Lett,89(3):992–1002. doi: 10.1785/0220170245
计量
- 文章访问数: 1220
- HTML全文浏览量: 556
- PDF下载量: 44
