Application of wavelet transform to the analysis of geoelectric field data
-
摘要: 随着城镇化发展的加快, 上海的地电场观测受到来自周围环境噪声的影响日益严重, 这些噪声干扰对于地震前兆异常的分析判断带来很多不确定性. 本文主要探讨通过小波变换方法来分解地电场观测原始信号, 分析环境噪声对原始观测数据的影响强度. 利用异常信号的小波模值对比分析了滤波结果, 并通过绘制极化方位图检验了该方法在实际运用中的效果. 结果表明: 数字滤波方法能很好地去除日常干扰所带来的背景噪声, 对于重构的地电场信号, 也能较好地反映其原始信号变化特征; 滤波后的自然电场异常信号保留了原始信号中主要的变化特征, 并能反映其原始变化规律; 重构的地电场信号能够突出信号中异常信号极化方位角, 使极化方位收敛有利于实际运用.Abstract: As urbanization gets into faster development, geoelectric field observation is affected by the electric signals from artificial interferences in Shanghai. It is difficult to distinguish such signals from signals of earthquake precursors. In this paper, the original signals of geoelectric field are decomposed by wavelet transform, and the intensity of background noise interference to original observation data are analyzed. We made a comparison between the original signals and filtered signals by analyzing Morlet wavelet transform modulus of abnormal signals, and tested the filtering effect in practical application by drawing azimuthal polarization plot. The results indicate that ① the method has a good performance in filtering background noises and the reconstructed signals of geoelectric field can well reflect the characteristics of original signals; ② the filtered signals of spontaneous electric field retain the variation tendency of original signals; ③ the reconstructed signals of geoelectric field can highlight the polarization characteristics of geoelectirc field and make the convergent polarization azimuth favorable to practical application.
-
Keywords:
- geoelectric field /
- interference /
- wavelet transform /
- dbN wavelet /
- polarization
-
引言
地电场是地球介质中的电场,普遍存在于地球表面. 根据场源的不同,地电场分为大地电场和自然电场. 大地电场源于高空电离层、 磁层等,具有日变特征,且影响范围较大; 自然电场主要源于地壳浅层,是由各种物理或化学作用而产生的,具有局部性特征,也是地震预测研究中重要的研究内容之一(钱家栋,林云芳,1995; 钱复业,赵玉林,2005; 高曙德等,2010). 地电场观测数据是地震前兆分析和研究的基础,然而,随着我国城市化、 工业化和现代化发展速度的加快,很多生活社区和大型工厂都向城市郊区迁移,大中型城市都已建有轨道交通系统. 而由此产生的工业游散电流、 轨道泄漏电流等对测区造成的影响,使得观测到的地电场信号受到了不同程度的干扰. 尤其当多个台站同时观测到自然电场异常信号时,由于观测数据所受干扰程度不一,加之各台站地下电性介质各向异性的影响(马钦忠等, 2004,2007),使得不同台站观测到的异常信号在原始形态上存有差异,这在很大程度上妨碍了对地震异常信号的分析辨别,所以通过运用信号处理的方法来了解原始数据中所包含的各种有用信息,对地震预报工作就显得尤为重要. 本文运用小波变换方法处理受到干扰的地电场数据,对干扰噪声进行分析,并运用小波系数重构的方法还原原始信号,通过滤波前后的数据对比分析检验了滤波效果,同时这也是数值信号处理方法在地电场多极距观测装置系统研究中的一个方面.
1. 小波变换与滤波
小波变换具有多分辨率分析的特点,在时间域和频率域都具有表征信号局部特征的能力,在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分(冉启文,谭立英,2002).
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

时,我们称Ψ(t)为一个基本小波. 对于连续情况,小波系列为

式中,a为伸缩因子,b为平移因子.
对于任意的函数f(t)∈L2(R)的连续小波变换为

其重构公式为

在数字信号处理中,对输入信号进行数字滤波,一般情况下是用一个阶梯函数来不断逼近原始输入信号,该阶梯函数与原始输入信号的相关程度越高,则所选阶梯函数与原输入信号的相似程度越好(郑治真等,2001).在阶梯函数中,充分大的阶段分解会使信号变得非常窄,这样就可以表示高频噪声. 在滤波时把这些非常窄的区间中所包含的信号设为零,就能得到一个接近于原始输入信号的去噪信号(刘明才,2005).本文将运用Daubenchies小波对上海青浦台、 崇明长江农场台(以下简称长江农场台)和崇明台地电场资料进行数字处理,分析其信号特征. Daubenchies小波简写为dbN,N表示小波的阶数. 随着N增大,小波尺度函数和小波函数的光滑性增强,对数字信号细节的描述能力也会增强,但此时紧支撑集中非零项的个数也会相应增加,一般为2N-1个非零项,这些非零项将会给信号重构带来不稳定性.
在一个全为零的时间序列中,施加了一个值为“1”的单点突跳干扰后,通过对dbN小波族中不同系数的对比分析,用db6小波重构的小波系数最大. 这也说明在dbN小波中,用db6小波尺度函数来处理单点突跳所得的信号相似部分与原始输入信号的相似程度最高. db6小波具有良好的连续性和光滑性,对信号重构也具有很好的稳定性,在数字信号处理中运用较多. 本文将采用db6小波对地电场资料进行分析.
2. 数据处理及分析
本文采用的数据资料是上海青浦台、 长江农场台和崇明台的地电场原始观测数据,选取的观测时间分别为2009年11月9日、 2010年12月28日和2010年8月4日. 在此观测时段内,3个台站分别记录到了自然电场异常信号,选取该时间段可以对自然电场异常信号在滤波前后的数据进行对比分析. 青浦台、 长江农场台和崇明台是“十五”新建和改造的地电台,观测仪器均为ZD9A-Ⅱ地电场仪. 青浦台采用“十”字型布极方式,南北和东西向长、 短极距分别为200 m和150 m; 长江农场台和崇明台采用三角形布极方式. 在这3段资料中,观测到的异常信号分别在不同台站的6个测道上都有明显记录,并在长、 短极距的观测上表现出一定的相似性. 根据地电场多极距观测系统理论判断,该异常信号很可能是一个自然电场异常信号. 在地电场多极距观测系统中,电极布设方向一般有东西向、 南北向和斜向,电极极距分为长极距、 短极距和斜长极距,随着地电场场源与观测台站方位的不同,在观测仪器各测向上记录到的曲线形态也有所差别. 根据观测曲线在不同测向上形态的差异,可以排除大部分的环境干扰信号,并可以由此判别哪些是自然电场异常信号,而自然电场变化特性正是地震预测研究的重要内容之一(马钦忠,2008).
本文运用小波变换的方法对该段数据资料进行分解和重构,从提取的噪声中来分析环境干扰对地电场观测的影响程度,同时讨论降噪后的地电场观测数据在自然电场异常信号识别中的作用.
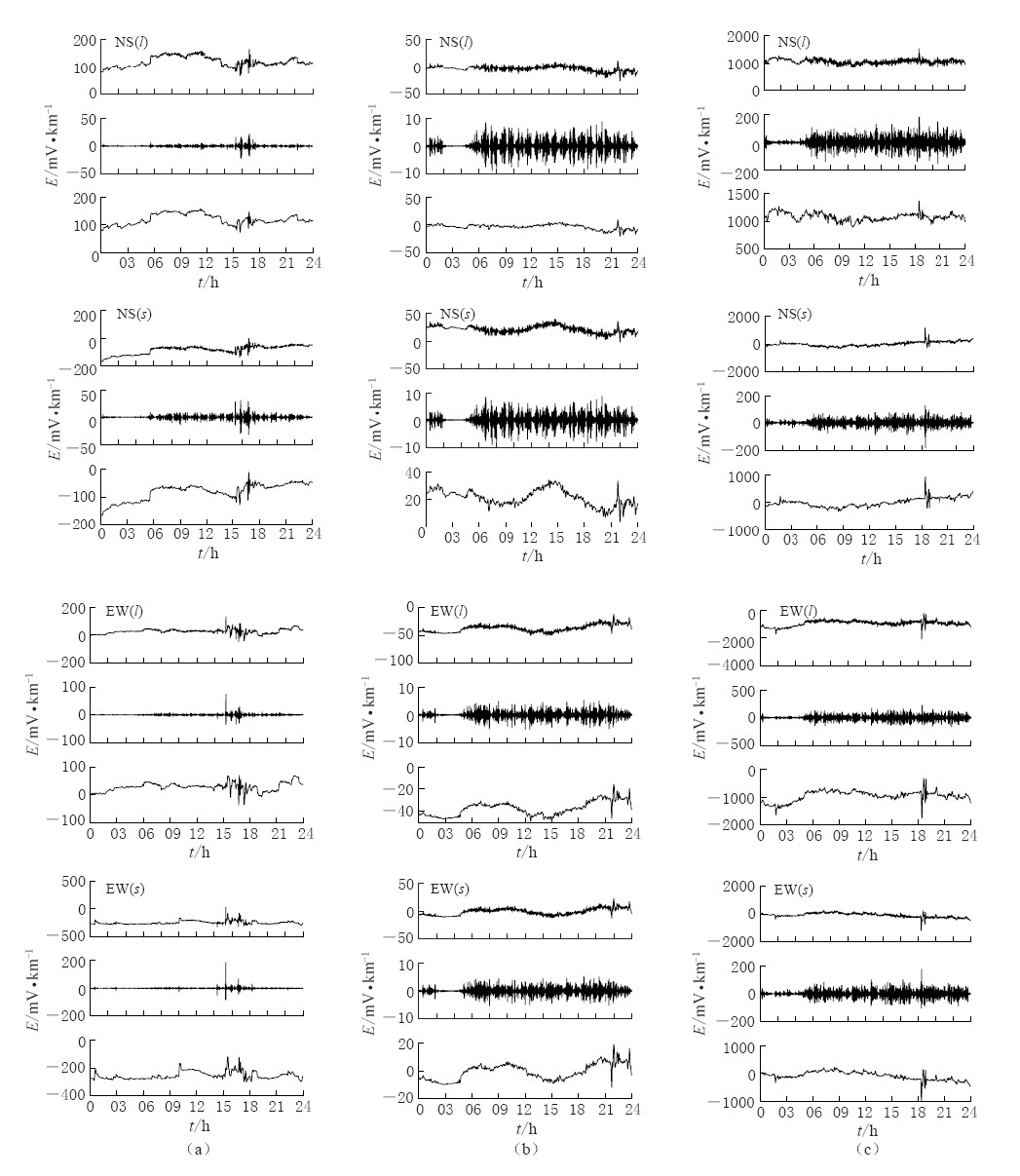
图 1中每一小图从上至下分别为地电场的原始数据曲线、 噪声曲线和重构结果. 图中电场强度(E)观测曲线在长极距和短极距上的形态相似度很高,但由于极距的不同,受干扰的程度也不同. 观测数据经过小波分解和重构后得到的结果已经剔除了大部分的噪声干扰. 青浦台南北向长极距的噪声干扰强度主要为±5 mV/km,异常信号中被滤除的噪声幅度为±23 mV/km,短极距干扰强度主要为±10 mV/km,异常信号中被滤除的噪声幅度为-32—33 mV/km; 东西向长极距噪声干扰强度范围主要为-6—8 mV/km,异常信号中被滤除的噪声幅度为-35—90 mV/km,而短极距噪声范围在-6—6 mV/km,异常信号中被滤除的噪声幅度为-90—220 mV/km. 长江农场台南北向长极距与短极距的噪声干扰强度主要为-8—10 mV/km,异常信号中被滤除的噪声变化幅度不明显; 东西向长极距与短极距噪声干扰强度范围主要为-5—4 mV/km,异常信号中被滤除的噪声变化幅度也同样不明显. 崇明台南北向长极距的噪声干扰强度主要为-80—70 mV/km,异常信号中被滤除的噪声幅度为-192—210 mV/km,南北向短极距强度主要为±60mV/km,异常信号中被滤除的噪声幅度为-415—380 mV/km; 东西向长极距噪声干扰强度范围主要为±160 mV/km,异常信号中被滤除的噪声幅度为-560—530 mV/km,而短极距噪声范围为±80 mV/km,异常信号中被滤除的噪声幅度为-400—413 mV/km. 从所有重构噪声的变化形态上可以看出,0—5时的噪声幅度要明显小于6—24时的噪声幅度,而6—24时这一时间段正是上海地铁的营运时间. 异常信号中被滤除的噪声明显有别于日常噪声的突跳部分,这也说明这些重构噪声中还包含着自然电场异常的信息. 但如果重构噪声的日变特征可靠,那么区分这些噪声中的有用信号是可以很容易做到的,这也是本文没有运用“自适应法”滤波的原因.
![]() 图 1 青浦台(a)、 长江农场台(b)和崇明台(c)地电场的原始数据曲线、 噪声曲线和重构结果NS(l), NS(s), EW(l), EW(s)分别表示南北向和东西向长、 短极距Figure 1. Original curves of geoelectric field, noise curves and reconstructed signals at Qingpu (a), Changjiang--nongchang (b) and Chongming (c) stationsNS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively
图 1 青浦台(a)、 长江农场台(b)和崇明台(c)地电场的原始数据曲线、 噪声曲线和重构结果NS(l), NS(s), EW(l), EW(s)分别表示南北向和东西向长、 短极距Figure 1. Original curves of geoelectric field, noise curves and reconstructed signals at Qingpu (a), Changjiang--nongchang (b) and Chongming (c) stationsNS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively为了进一步了解重构信号与原始数据的差异,检验滤波方法会否对原始数据中的有用部分造成破坏,运用小波时频局部化的特性(韩延本,韩永刚,2001),对地电场观测数据中自然电场异常部分进行小波功率谱分析. 考虑到原始数据中被滤去的噪声是信号的高频部分,小波功率谱实质是对小波模值的平方进行积分,这样处理对高频噪声有放大作用,而且本文主要是研究滤波前后数据原有特征的变化情况,所以运用小波模值的分析方法能更好地反应滤波前后数据中高频部分的变化情况. 由于篇幅所限,此处只选用了青浦台2009年11月9日的地电场观测数据进行对比分析. 本文选用Morlet小波为基本小波,其在允许条件下的表达式为(乐贵明,王家龙,2004)

由于Morlet小波是复小波(夏洪瑞,2008; 高静怀等,1997),其小波模值的计算表达式可以写为

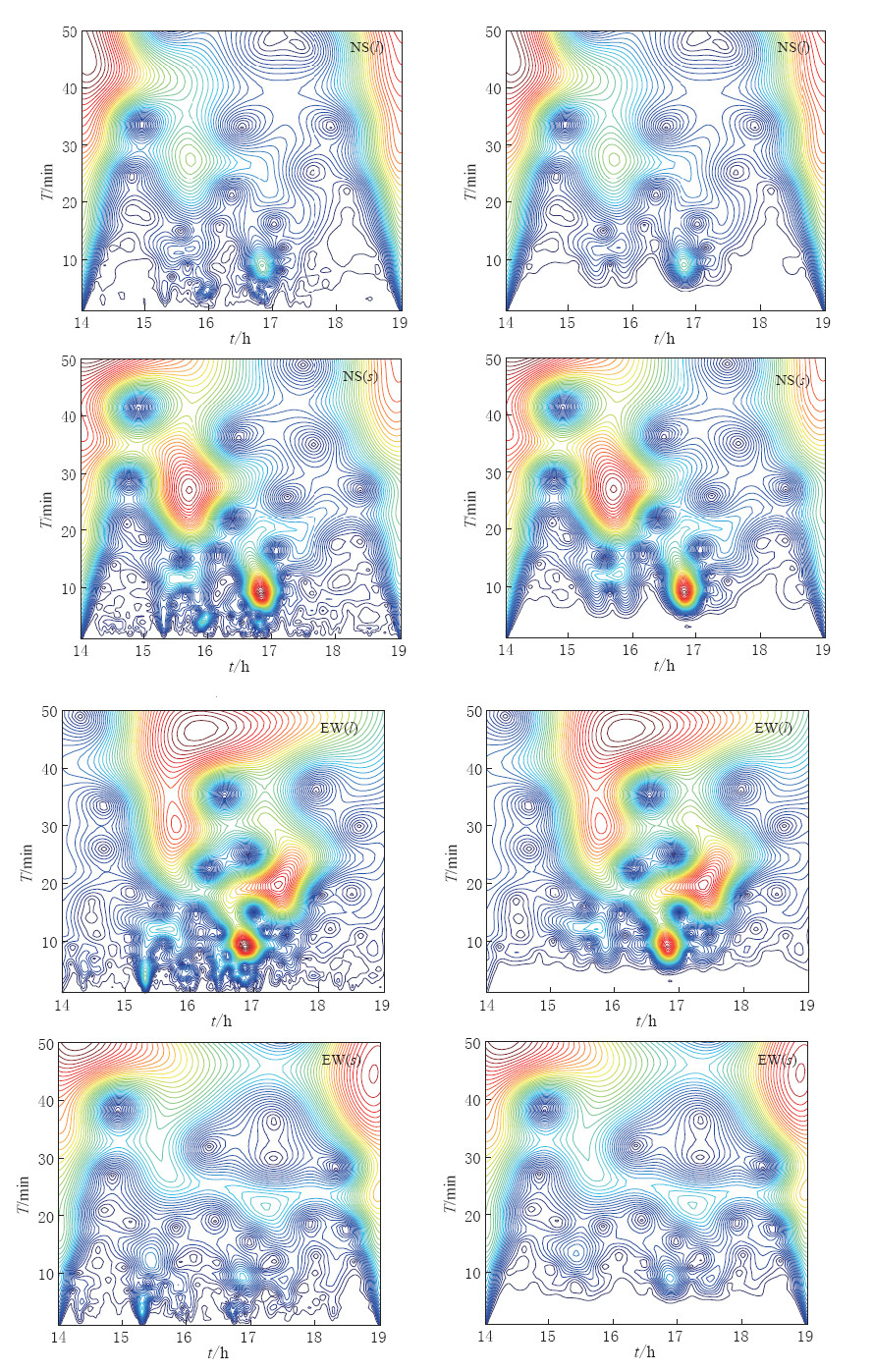
图 2是2009年11月9日14—19时青浦地电场台南北向、 东西向的原始数据和滤波后数据的小波模值. 图中,等值线圆表示在该时段出现的扰动能量的变化情况,颜色深浅表示能量的强弱. 从图 2可以看出,数值滤波处理结果基本上保留了原始数据中固有的能量变化特征,其等值线圆的位相基本不变. 对于原始数据中变化周期大于5分钟的异常扰动,滤波前后其位相变化基本上保持不变; 对于变化周期小于5分钟的扰动,滤波后其变化特征已基本被消除. 通过对原始数据中15时15分—17时41分出现的自然电场异常信号的对比分析可以看出,数值滤波后异常信号的相位变化仍然明显,且与原始数据中的相位变化有较好的对应. 这说明,对原始数据的滤波只滤除了数据中的短周期变化,而对于相对长周期的自然电场异常信号则不会产生影响.
![]() 图 2 2009年11月9日14—19时青浦台地电场异常信号原始数据与处理结果 的Morlet小波模值对比图(左侧为原始数据, 右侧为处理结果)NS(l), NS(s), EW(l), EW(s)分别为南北向和东西向长、 短极距Figure 2. Morlet wavelet transform modulus contour of the original abnormal geoelectric field data and the calculated data for 14:00—19:00 on Nov. 9, 2009, at Qingpu stationLeft plots show original data and right denote calculated data. NS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively
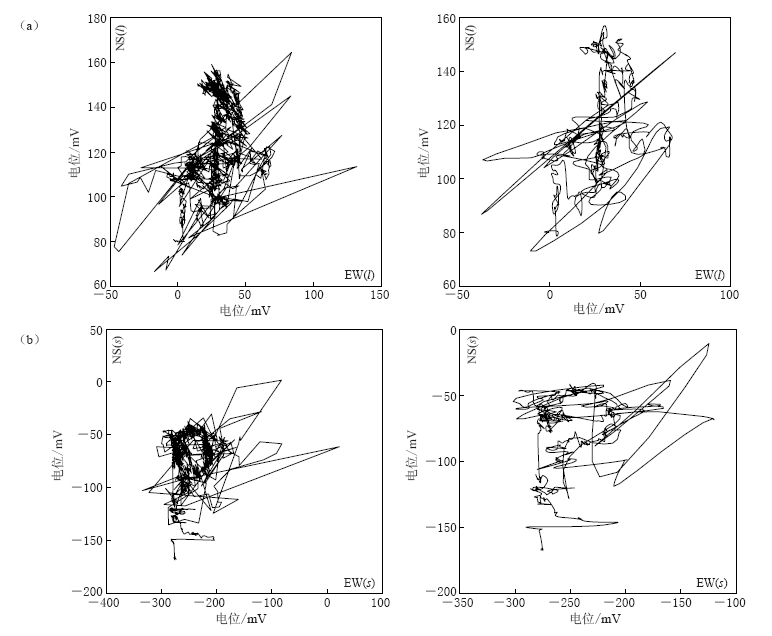
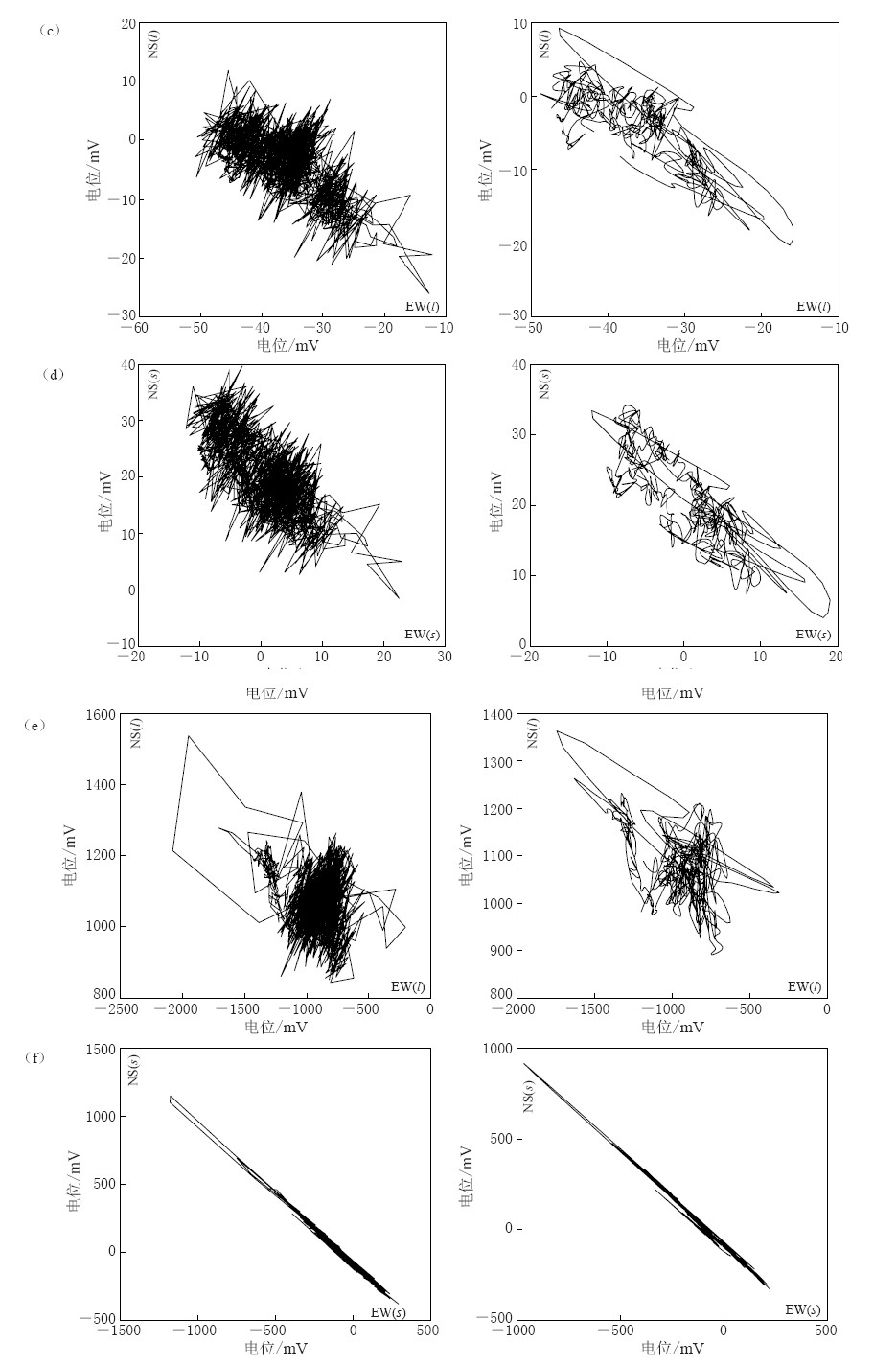
图 2 2009年11月9日14—19时青浦台地电场异常信号原始数据与处理结果 的Morlet小波模值对比图(左侧为原始数据, 右侧为处理结果)NS(l), NS(s), EW(l), EW(s)分别为南北向和东西向长、 短极距Figure 2. Morlet wavelet transform modulus contour of the original abnormal geoelectric field data and the calculated data for 14:00—19:00 on Nov. 9, 2009, at Qingpu stationLeft plots show original data and right denote calculated data. NS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively目前地电场极化方向的研究在地电场观测资料分析、 观测台站特性研究和地震震例分析中已经得到了广泛的运用(阮爱国,赵和云,2000; 郑兆苾,汪雪泉,2005; 张学民,卢军,2007). 本文运用该方法主要是为了分析并检验运用小波变换滤波前后观测资料的变化情况,以及本研究在实际运用中的效果. 图 3a,b为2009年11月9日青浦台地电场原始观测资料与处理结果分别在长极距和短极距测向上的极化图. 从图 3a左侧图中可以看出青浦台地电场原始资料的极化特性很差,整体看不出明显极化方向角,这应该与观测台站所受到的干扰有直接关系. 图 3a右图中虽然极化特性也很差,但从图中可以看出,在该日的某一时段内,观测资料存在较为明显的极化方向. 通过对经过滤波处理后资料的分析,这一明显的极化方向正好与该日自然电场异常资料相对应. 通过处理后,青浦台短极距的极化方向则更加明确,大致与长极距极化方向相同,都为北东向(图 3b). 长江农场台地电场原始观测数据在经过处理后,极化方向变得收敛,极化方位角度则更加明确(图 3c,d). 崇明台长极距的极化特性较差,但经过处理后的结果在某一时段内则表现出明显的极化方向(图 3e),而短极距则有较好的极化特性(图 3f).
![]() 图 3 (c--f) 长江农场台和崇明台地电场极化图(左侧为原始数据, 右侧为处理结果)(c), (d)分别为长江农场台长极距极化图和短极距极化图; (e), (f)分别为崇明台长极距极化图和短极距极化图Figure 3 (c--f). Azimuthal polarizations at Changjiang--nongchang and Chongming stationsLeft plots denote original data and right display calculated data. (c) and (d) show polarizations obtained from observations of long dipole and short dipole, respectively, for Changjiang--nongchang station; (e) and (f) are polarizations obtained from observations of long dipole and short dipole, respectively, for Chongming station
图 3 (c--f) 长江农场台和崇明台地电场极化图(左侧为原始数据, 右侧为处理结果)(c), (d)分别为长江农场台长极距极化图和短极距极化图; (e), (f)分别为崇明台长极距极化图和短极距极化图Figure 3 (c--f). Azimuthal polarizations at Changjiang--nongchang and Chongming stationsLeft plots denote original data and right display calculated data. (c) and (d) show polarizations obtained from observations of long dipole and short dipole, respectively, for Changjiang--nongchang station; (e) and (f) are polarizations obtained from observations of long dipole and short dipole, respectively, for Chongming station从3个台站的地电场极化情况来看,在目前的观测环境下要想获得理想的地电场极化方位是比较困难的,通过滤波的方式来处理数据在一定程度上可以解决观测环境变化给数据观测质量带来的问题. 小波变换的目的主要是针对地电场中存在的噪声进行滤波,如果只对某一时段地电场异常的原始数据和处理后数据进行极化特性的对比分析,那么可能会得到更为收敛的极化方向,这对判断自然电场异常场源方向具有十分重要的作用.
3. 结论
在地电场地震前兆信息资料分析中,对地电场数据的滤波并不是主要目的,其最主要的任务是尽可能多地了解这些数据中所包含的信息,从这些信息中提取我们需要的地震前兆信号. 由于地下电性介质的各向异性以及干扰源的差异性,地电场观测在长、 短极距之间的观测结果会出现一定的差异,异常信号出现的时间和突跳幅度在表现形式上也会不同. 如果用这些原始观测数据来分析地震前兆信息则很可能会出现大相径庭的结果,只有加强对观测数据的理解才能了解这些数据所反映的真实信息. 通过对原始数据的分解与重构,将原始数据中包含的干扰信息分离出来,使处理后的观测数据更加真实地反映地震前兆异常,并加深对观测数据所包含物理过程的理解,我们才可以去除不稳定的干扰,使观测到的异常信号保持一定的稳定性. 在此基础上,再用这些相对稳定的数据去分析地电场的变化特性,这样对地震前兆的确定是有益处的. 本文通过对地电场信号的滤波分析了解了噪声信号的干扰范围、 影响时间和干扰强度等重要信息,这对今后地电场数据的分析有一定现实意义.
本文通过小波变换方法对上海3个台站在不同时间段观测到的地电场资料进行分析,得到以下的初步结论:
1)本文中运用的小波变换方法能对原始观测数据进行分解和重构,并滤除地电场观测中记录到的地铁噪声等干扰,滤除的噪声干扰呈现出0—5时减弱,6—24时增强的特征. 重构后的地电场信号能较好地还原原始信号的变化特征. 由于该方法在计算过程中不需要特殊设置,只需在基本小波的选取上做适当调整,所以该方法有一定的实用性.
2)从小波模值的处理结果可以看出,该方法不会对地电场观测数据中不同频率的异常信号造成破坏,而且处理还原后的异常信号能很好地反映异常变化的整体形态.
3)对于所分析的这3个地电场台,通过小波变换重构的数据能较好地反映该台站的极化特性,尤其是在观测数据出现异常的情况下,能够收敛并明确异常数据的极化方向.
-
图 1 青浦台(a)、 长江农场台(b)和崇明台(c)地电场的原始数据曲线、 噪声曲线和重构结果
NS(l), NS(s), EW(l), EW(s)分别表示南北向和东西向长、 短极距
Figure 1. Original curves of geoelectric field, noise curves and reconstructed signals at Qingpu (a), Changjiang--nongchang (b) and Chongming (c) stations
NS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively
图 2 2009年11月9日14—19时青浦台地电场异常信号原始数据与处理结果 的Morlet小波模值对比图(左侧为原始数据, 右侧为处理结果)
NS(l), NS(s), EW(l), EW(s)分别为南北向和东西向长、 短极距
Figure 2. Morlet wavelet transform modulus contour of the original abnormal geoelectric field data and the calculated data for 14:00—19:00 on Nov. 9, 2009, at Qingpu station
Left plots show original data and right denote calculated data. NS(l), NS(s), EW(l) and EW(s) represent the long dipoles and short dipoles in NS and EW directions, respectively
图 3 (c--f) 长江农场台和崇明台地电场极化图(左侧为原始数据, 右侧为处理结果)
(c), (d)分别为长江农场台长极距极化图和短极距极化图; (e), (f)分别为崇明台长极距极化图和短极距极化图
Figure 3 (c--f). Azimuthal polarizations at Changjiang--nongchang and Chongming stations
Left plots denote original data and right display calculated data. (c) and (d) show polarizations obtained from observations of long dipole and short dipole, respectively, for Changjiang--nongchang station; (e) and (f) are polarizations obtained from observations of long dipole and short dipole, respectively, for Chongming station
-
高静怀, 汪文秉, 朱光明. 1997. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 40(6): 821-832. 高曙德, 汤吉, 杜学彬, 刘小凤, 苏永刚, 陈彦平, 狄国荣, 梅东林, 詹艳, 王立凤. 2010. 汶川8.0级地震前后电磁场的变化特征[J]. 地球物理学报, 53(3): 512-525. 韩延本, 韩永刚. 2001. 太阳黑子相对数变化的小波分析[J]. 科学通报, 46(24): 2031-2035. 乐贵明, 王家龙. 2004. 太阳黑子相对数最强周期的小波分析[J]. 地球物理学报, 47(5): 743-746. 刘明才. 2005. 小波分析及其运用[M]. 北京: 清华大学出版社: 11-15. 马钦忠, 冯志生, 宋志平, 赵卫国. 2004. 崇明与南京台震前地电场变化异常分析[J]. 地震学报, 26(3): 304-312. 马钦忠, 席继楼, 蔡晋安, 汪育新. 2007. 天然场源对地电场观测中的贡献研究[J]. 地震, 27(增刊): 131-137. 马钦忠. 2008. 地电场多极距观测装置系统与文安MS5.1地震前首都圈地电场异常研究[J]. 地震学报, 30(6): 615-625. 钱复业, 赵玉林. 2005. 地电场短临预报方法研究[J]. 地震, 25(2): 33-40. 钱家栋, 林云芳. 1995. 地震电磁观测技术[M]. 北京: 地震出版社: 6-9. 冉启文, 谭立英. 2002. 小波分析与分数傅里叶变换及应用[M]. 北京: 国防工业出版社: 22-26. 阮爱国, 赵和云. 2000. 提取地震地电场异常的垂直极化方向投影法[J]. 地震学报, 22(2): 171-175. 夏洪瑞. 2008. 应用Morlet小波进行地震资料属性提取效果分析[J]. 勘探地球物理进展, 31(2): 117-121. 张学民, 卢军. 2007. 腾冲台强震前地电场线性极化特性[J]. 地震, 27(2): 90-98. 郑兆苾, 汪雪泉. 2005. 蒙城台地电场资料分析[J]. 地震, 25(2): 41-47. 郑治真, 沈萍, 杨选辉, 万玉莉. 2001. 小波变换及其MATLAB工具的应用[M]. 北京: 地震出版社: 94-98. -
期刊类型引用(16)
1. 范晓易,王巍,曲均浩,李伟,陈飞. 城市轨道交通沿线地电监测仪器干扰分析与抑制处理. 中国铁道科学. 2022(06): 186-193 .  百度学术
百度学术
2. 李瑞卿,郭学增,张蕾,信世民,尹宏伟. 地电场电极故障判定及机理分析. 地震工程学报. 2020(02): 438-446 .  百度学术
百度学术
3. 汪凯翔,黄清华,吴思弘. 长短时记忆神经网络在地电场数据处理中的应用. 地球物理学报. 2020(08): 3015-3024 .  百度学术
百度学术
4. 冯红武,颜文华,王建昌,闫俊义. 地电场观测中城市轨道交通干扰剔除. 地震地磁观测与研究. 2019(03): 70-78 .  百度学术
百度学术
5. 王晓蕾,谷国梁,马义山,刘传军,徐小远,杨建思. 塘沽地电阻率观测轻轨干扰降噪处理. 地震地磁观测与研究. 2019(04): 81-88 .  百度学术
百度学术
6. 朱杰. 元谋地电场观测数据小波阈值去噪. 地震地磁观测与研究. 2019(05): 70-78 .  百度学术
百度学术
7. 胡小静,毕青,付虹. 大地电场观测中干扰变化的特征分析. 地震. 2017(02): 157-166 .  百度学术
百度学术
8. 高曙德. 深井地电观测技术在地震监测中的应用探讨. 地球物理学进展. 2016(05): 2078-2088 .  百度学术
百度学术
9. 赵俊香,朱培育,毕波,朱佳苗,施俊杰,杜励,龚耀. 崇明地电场地铁干扰分析. 地震地磁观测与研究. 2016(02): 124-129 .  百度学术
百度学术
10. 强玉华,智协飞,杨磊. 浙西南冰雹天气雷电及大气电场活动规律研究. 科技通报. 2016(12): 21-26+46 .  百度学术
百度学术
11. 龚耀,李伟,马钦忠,周江南. 上海崇明地震台地电场观测影响因素分析与研究. 山西地震. 2016(01): 31-36 .  百度学术
百度学术
12. 李伟,马钦忠,宋先月,方国庆,周江南,赵文舟. 上海地区电磁辐射信号特征及其与大震的关系研究. 地震工程学报. 2016(S1): 65-72 .  百度学术
百度学术
13. 殷文. 基于时频约束的井震资料联合时深标定方法. 成都理工大学学报(自然科学版). 2015(03): 377-384 .  百度学术
百度学术
14. 罗娜,王利兵,王静,宋昭,赵永红,李细顺,贾华,陈凯男,赵志远. 基于小波模极大值的地震信号去噪研究. 山西地震. 2015(02): 12-15+23 .  百度学术
百度学术
15. 赵文舟,马钦忠,李伟. 杂散电流腐蚀及防护研究现状. 地震地磁观测与研究. 2014(Z2): 320-325 .  百度学术
百度学术
16. 李伟,马钦忠,王冠玥. 地电场多极距观测的异常识别和分析. 中国地震. 2014(01): 91-101 .  百度学术
百度学术
其他类型引用(7)




 下载:
下载: