Characterization of tail distribution of earthquake magnitudes via generalized Pareto distribution
-
摘要: 极值理论在地震危险性分析中有着重要应用, 发震震级超过某一阈值的超出量分布可以近似为广义帕累托分布. 基于广义帕累托分布给出了若干地震活动性参数的估计公式, 包括强震震级分布、 地震复发周期和重现水平、 期望重现震级、 地震危险性概率和潜在震级上限等; 以云南地区震级资料为基础数据, 讨论了阈值选取、 模型拟合诊断和参数估计; 在此基础上计算了该地区的地震活动性参数. 结果表明, 广义帕累托分布较好地刻画了强震震级分布, 通过超阈值(POT)模型计算的复发周期与实际复发间隔统计基本一致, 高分位数估计在一定阈值范围内表现稳定, 为工程抗震中潜在震级上限的确定提供了一种途径.Abstract: Extreme value theory in seismic risk analysis has important application, and the excess of earthquake magnitude distribution over a threshold can be approximated by generalized Pareto distribution. Based on the generalized Pareto distribution, we developed several estimation formulas of seismic activity parameters, including strong earthquake magnitude distribution, earthquake recurrence period and return level, expected recurrence magnitude, probability of seismic risk and maximum earthquake magnitude; then, based on historical seismic data in Yunnan region, we discussed how to choose the threshold value, model fitting diagnosis and parameter estimation. Finally we calculated seismicity parameters in the region. The results show that generalized Pareto distribution characterized strong earthquake magnitude distribution quite satisfactorily, the recurrence periods by POT (peaks over threshold method) model agree with the actual recurrence interval statistics, and the high quantile is stable within a specific threshold range. So the generalized Pareto distribution is a possible approach to determining the potential upper limit earthquake magnitude in engineering seismology.
-
引言
极值统计在地震预报、 地震危险性分析、 工程地震安全性评价及地震区划等诸多地震学领域有着广泛应用(Epstein,Lomnitz,1966; Yegulalp,Kuo,1974; 陈培善,林邦慧,1973; 高孟潭,贾素娟,1988; 陈虹,黄忠贤,1995; 贾素娟,鄢家全,1996). 极值分布有3种类型: Gumbel(Ⅰ型)、 Frechet(Ⅱ型)、 Weibull(Ⅲ型),它们可以统一为广义极值分布. 钱小仕等(2012)基于广义极值分布给出了若干地震预报分析的公式与方法,并以台湾地区为震例进行了研究,拓展了极值理论的应用范围. 但是利用极值分布作统计分析的不足是仅能利用所研究时间窗中单个数据点信息. 例如在估计最大地震震级分布时,仅使用了年或给定时间区间上最大震级数据,严重制约着获得稳健分布参数估计的数据规模,导致参数估计的统计稳定性降低,概率地震危险性预测的不确定性增大. Balkema和de Haan (1974)以及Pickands (1975)指出,对于充分大的阈值,随机变量超过阈值的超出量的极限分布为广义帕累托分布(generalized Pareto distribution,简写为GPD),为研究随机变量尾部特征提供了统计理论依据. 近年来,国外已有学者将广义帕累托分布引入地震研究,Pisarenko和Sornette (2003)利用广义帕累托分布分析了哈佛地震目录中18个地震区的浅层地震地震矩分布; Huyse等(2010)利用太平洋地震工程研究的地面峰值加速度(PGA)数据和基于Abrahamson-Silva衰减模型的PGA残差数据,比较了对数正态分布与广义帕累托分布的拟合优度.
本文基于广义帕累托分布给出了若干地震活动性参数的估计方法,包括强震震级分布、 地震平均复发周期、 重现水平和期望重现震级、 地震危险性概率和潜在震级上限估计等; 利用超阈值(peaks over threshold,简写为POT)模型对云南地区历史地震资料进行分析,估计该地区强震震级分布并与G-R经验关系作比较; 在此基础上计算了各震级档复发时间和未来几年发震危险性.
1. 广义帕累托分布与POT模型
设X1,X2,…,Xn为地震震级随机变量列,假设它们相互独立且服从同一分布F(x),记其最大震级为Mn=max(X1,X2,…,Xn),若存在{an>0,bn∈R}和非退化分布函数H(x), 使

则称H(x)为极值分布,而称分布F(x)属于极值分布H(x)的最大值吸引场. Fisher和Tippett(1928)获得了极值分布的3种形式,它们也可以统一为广义极值分布

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

为地震震级X的超过阈值u的超出量的分布函数,简称超出量分布. Balkema和de Haan (1974)以及Pickands(1975)指出,当震级分布F属于极值分布H的最大值吸引场时有

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
2. POT模型的应用
This page contains the following errors:
error on line 1 at column 77: Extra content at the end of the documentBelow is a rendering of the page up to the first error.
钱小仕等(2012)2.1 强震震级分布估计
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

或者分布函数的估计

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

仍为广义帕累托分布,且形状参数保持不变. 因此,基于超阈值震级分布的POT模型具有理论上的阈值分布稳定性.
2.2 平均复发周期估计
假设地震数据为日观测数据,一年按365天计算,若震级分布为广义帕累托分布G(x; u,,ξ),则发生震级为x的地震平均复发周期为

2.3 重现水平估计
对给定概率p,根据式(5)不超过概率p的发震震级(即p-分位数)为

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
重现水平估计只是估计了发震超过某一震级的可能性,不能确定当超过该震级地震发生时可能的地震震级大小. 为解决这一问题,我们提出期望重现震级概念,以期为发震震级预测提供一种新的途径. 称E(X | X>xp)为期望重现震级,表示当发震震级超过特定水平xp下该震级平均大小,记为 p, 则

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

2.4 地震危险性概率
未来T年发震震级超过x的概率

2.5 潜在震级上限估计
当形状参数ξ<0时,对应分布有有限右端点,即震级分布有上限

3. 实例分析
3.1 资料选取
2005年10月31日前的数据引自国家自然科学基金委员会“中国西部环境与生态科学数据中心”(http://westdc.westgis.ac.cn) ① . 该目录包括公元前2300年—公元2005年间发生在全国各地的各级地震,共33万余条目录,每条包括发震时间、 震中经纬度、 震源深度和震级. 2005年11月1日—2010年12月31日数据引自中国地震信息网(http://www.csi.ac.cn)提供的测震目录② . 地震震级采用面波震级MS,在MS缺失部分利用面波震级MS与近震震级ML之间的转换关系式(汪素云等,2010): MS=1.13ML-1.08,将近震震级转换为MS. 从中选取云南地区(21°—29°N,97°—106°E)1900—2010年地震目录(包含四川省与中缅交界地区的部分地震),并进行余震删除. 余震删除方法采用C-S余震时空窗(陈凌等,1998),经余震删除后共有74 159个震级数据,其中MS≥5.0地震共539次,MS≥6.0地震122次,MS≥7.0地震17次
①马瑾,等. 2005. 中国地震目录. 中国地震局地质研究所. [2011-11-09]http://westdc.westgis.ac.cn/data/236a607a-245f-4444-ba4c-f7cccfd53271.
②中国地震台网中心. 2012. 中国地震台网(CSN)地震目录. 中国地震台网中心. [2011-11-15]http://www.csndmc.ac.cn/newweb/catalog_direct_link.htm.
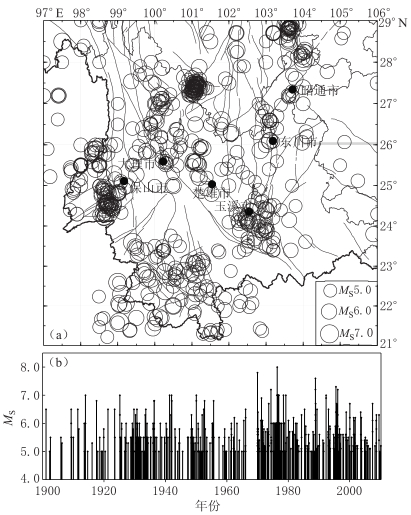
由于POT模型主要针对震级分布的尾部,即强震震级特征的分析,因此需考虑强震目录的完整性. 图1给出了1900—2010年云南地区MS≥5.0地震的震中分布和M-t图. 由图1b可见,大致在1930年前后,地震记载开始丰富起来. 相关研究表明,20世纪30年代以后该地区5级以上地震记录才较为完整(黄玮琼等,1994; 皇甫岗,李中华,2010; 苏有锦,李中华,2011). 结合本文阈值的选择,我们选取1930年作为5级以上地震目录基本完整的起始年代. 共获得74 102个震级数据,其中MS≥5.0地震共487次,MS≥6.0地震107次,MS≥7.0地震15次. 为了比较广义帕累托分布与基于G-R关系的指数分布的拟合效果,我们选择震级数据较好地符合G-R关系式的最小震级作为起始震级. 图2给出了1930—2010年的G-R关系拟合. 从图中可以看出,云南地区MS≥2.0的地震较好地符合G-R关系式,MS<2.0地震明显偏离上述关系,因此本文震例计算中,震级下限取为MS≥2.0.
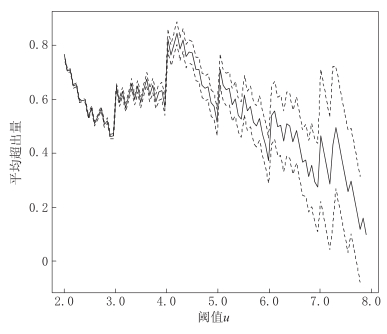
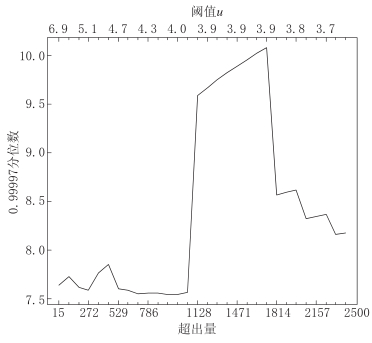
3.2 阈值选取与模型诊断
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
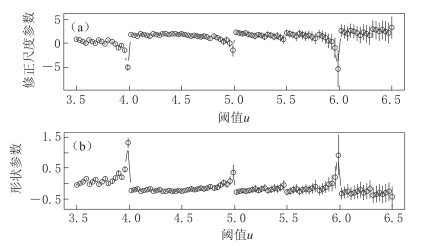
图4给出了广义帕累托分布参数估计在不同阈值选取下的变化图,其中修正的尺度参数为σ*= -ξu. 对于适当选定的阈值,相应的超出量服从广义帕累托分布,则形状参数和修正的尺度参数的估计应保持不变. 从图4可以看出,当阈值约在区间(4.0,5.0)时,参数估计比较稳定. 根据极值理论,为保证极值模型的准确性,应在参数估计值与所选阈值附近呈平稳性的基础上尽量选取较大的阈值,所以我们取云南地区震级尾部阈值为u=5.0. 此时,超阈值数据达320个,约占总量(48 456)的0.66%,不超过1%,因此可以较好地满足尾部极值建模的条件.
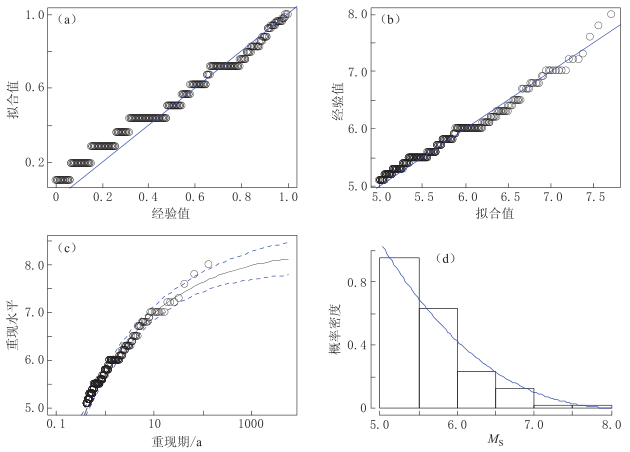
阈值选定后,需对广义帕累托分布拟合状况进行诊断. 图5a为P-P图,图5b为Q-Q图,图5c为重现水平图,图5d为尾部密度曲线的估计和直方图. P-P图是根据变量的累积概率与指定分布的累积概率之间的关系绘制的图形. Q-Q图是用变量数据分布的分位数与指定分布的分位数之间的关系绘制的图形. 如所检验的数据符合指定的分布,则P-P图和Q-Q图上的点应近似在一条直线上. 重现水平图为重现期的对数与重现水平之间关系绘制的图形,如所检验数据符合广义帕累托分布,则样本数据应落在给定分布分位数估计置信区间内. 从图5中可以看出,各散点数据基本紧密围绕各参考线分布,表明拟合状态良好,利用POT模型分析云南地区震级分布特征较适宜.
3.3 地震活动性参数估计
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
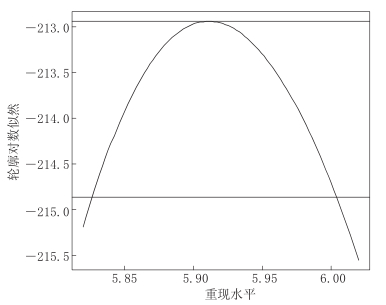
苏有锦和李中华(2011)研究了云南地区6级以上强震时间分布特征,统计得到MS≥6.0平均间隔1.27 a,MS≥6.5平均间隔2.75 a,MS≥7.0平均间隔8.21 a,实际地震有60%以上均发生在平均间隔时间内. 本文利用广义帕累托分布估计相应复发 时间间隔的震级水平. 图7是重现期为1.27 a 的震级重现水平轮廓似然函数图,复发震 级的最大似然估计为MS=5.91,95%的置信区间为[5.82,6.01]. 类似地,表1给出了各重现期的地震复发震级估计和95%的置信区间以及期望重现震级的估计. 表2给出了云南地区各强震复发周期预测和未来1 a,5 a的发震概率. 从表1的点估计和表2的复发周期可以看出,基于广义帕累托分布估计的复发震级和复发周期,与苏有锦和李中华(2011)的结果基本一致,各震级复发周期相对于苏有锦和李中华(2011)平均复发间隔稍高,但均处于0.5σ方差线内. 表2的概率估计表明,云南地区未来一段时间内5—6级地震发生危险性较高.
Gutenberg和Richter (1956)提出的震级-频度经验公式,已成为地震学中最基础的定律之一,在地震活动性研究与地震危险性预测的实践中被广泛引用. 在地震活动平稳性假设下,相当于地震震级分布为指数分布(陈培善,林邦慧,1973). 图8给出了云南地区MS≥5.0地震资料的经验分布(圆圈)、 基于广义帕累托分布的震级分布拟合(实线)和基于G-R关系式的指数分布拟合(虚线)比较. 从图8可以看出,在尾部区域对给定的尾概率水平1-F(x),G-R经验关系在5—6级段低估而在7级以上高估发震震级或危险性,而广义帕累托分布的估计总体上与实际数据拟合良好,而且给出了震级应有上限的一种自然描述,无需像指数分布那样通过人为的右截断(Cosentino et al,1977)来描述震级分布.
4. 讨论与结论
一般说来,基于独立同分布随机变量的极值建模有两种基本统计模型: 一种是经典的极值分析区组最大值法 仅利用研究时间窗中最大值数据信息; 另一种是超阈值分析POT方法 利用超过给定阈值的所有数据信息. 本文基于广义帕累托分布给出了地震活动性分析的几种公式,包括强震震级分布的估计、 重现期与重现水平的预测、 给定时间内地震危险性概率和震级上限的确定等,利用POT模型对云南地区历史地震资料进行分析. 结果表明,云南地区震级资料用广义帕累托分布拟合较好,在参数估计的基础上,获得云南地区强震震级分布为F(x)=1-0.006 6[1-0.3(x-5)]3.484,x≥5. 通过与G-R关系式的对比发现,基于G-R关系的指数分布在强震级端可能或低或高地估计了地震危险性,而基于POT模型的广义帕累托分布则与实际资料吻合良好,而且POT模型具备严格的数学理论依据.
最大地震震级是描述区域地震活动性的一个基本参数,地震学家们已发展了多种最大地震震级的确定方法(陈颙,陈凌,1999),对各种震级上限确定方法的不确定性也有研究(冉洪流,2009). 本文指出若震级分布可以用广义帕累托分布拟合,则最大震级及其不确定性可以通过参数估计方法得到,为确定震级上限增添了一种新的途径.
本文基于广义帕累托分布的云南强震复发时间的估计,与苏有锦和李中华(2011)通过对实际地震资料发震间隔统计得到的结果基本一致,表明利用POT模型估计地震复发时间具有一定的实际意义. 对云南地区未来1 a,5 a强震发生概率的估计可以发现,未来该地区中强震发生的危险性偏高,应引起重视.
重现水平估计只是给出了超过某一震级档地震发生的可能,不能确定实际可能发生的地震大小. 本文提出了期望重现震级概念,计算在超过某震级地震发生时发震震级的平均大小. 关于期望重现震级在实际应用中的效果,还有待进一步研究.
-
-
陈虹, 黄忠贤. 1995. 应用混合极值理论及最大似然法估计中国大陆地震危险性[J]. 地震学报, 17(2): 264-269. 陈凌, 刘杰, 陈颙, 陈龙生. 1998. 地震活动性分析中余震的删除[J]. 地球物理学报, 41(增刊): 244-252. 陈培善, 林邦慧. 1973. 极值理论在中长期地震预报中的应用[J]. 地球物理学报, 16(1): 6-24. 陈颙, 陈凌. 1999. 地震危险性分析中最大地震震级的确定[J]. 地球物理学报, 42(3): 351-357. 高孟潭, 贾素娟. 1988. 极值理论在工程地震中的应用[J]. 地震学报, 10(3): 317-326. 黄玮琼, 李文香, 曹学峰. 1994. 中国大陆地震资料完整性研究之二: 分区地震资料基本完整的起始年分布图[J]. 地震学报, 16(4): 423-432. 皇甫岗, 李中华. 2010. 20世纪云南地区地震记录完全性评价[J]. 地震研究, 33(1): 1-6. 贾素娟, 鄢家全. 1996. 利用历史地震影响烈度的统计特性进行地震区划[J]. 地震研究, 19(3): 277-285. 钱小仕, 王福昌, 曹桂荣, 任晴晴. 2012. 广义极值分布在地震危险性分析中的应用[J]. 地震研究, 35(1): 73-78. 冉洪流. 2009. 潜在震源区震级上限不确定性研究[J]. 地震学报, 31(4): 396-402. 史道济. 2006. 实用极值统计方法[M]. 天津: 天津科学技术出版社: 83-85. 苏有锦, 李中华. 2011. 云南地区6级以上强震时间分布特征及其概率预测模型研究[J]. 地震研究, 34(1): 1-7. 汪素云, 高阿甲, 冯义钧, 和锐. 2010. 中国地震目录间的对比及标准化[J]. 地震, 30(2): 38-45. Balkema A A, de Haan L. 1974. Residual life time at great age[J]. Ann Probab, 2(5): 792-804.
Cosentino P, Ficara V, Luzio D. 1977. Truncated exponential frequency-magnitude relationship in the earthquake statistics[J]. Bull Seism Soc Amer, 67(6): 1615-1623.
Epstein B, Lomnitz C. 1966. A model for the occurrence of the largest earthquakes[J]. Nature, 211(5052): 954-956.
Fisher R, Tippett L H. 1928. Limiting forms of the frequency distributions of the largest or smallest member of a sample[J]. Proc Camb Phil Soc, 24(2): 180-190.
Gutenberg B, Richter C. 1956. Earthquake magnitude, intensity, energy, and acceleration, part Ⅱ[J]. Bull Seism Soc Amer, 46(2): 105-145.
Huyse L, Chen R, Stamatakos J A. 2010. Application of generalized pareto distribution to constrain uncertainty in peak ground accelerations[J]. Bull Seism Soc Amer, 100(1): 87-101.
Pickands J. 1975. Statistical inference using extreme order statistics[J]. Ann Stat, 3(1): 119-131.
Pisarenko V F, Sornette D. 2003. Characterization of frequency of extreme earthquake events by the generalized pareto distribution[J]. Pure Appl Geophys, 160(12): 2343-2364.
Yegulalp T M, Kuo J A. 1974. Statistical prediction of the occurrence of maximum magnitude earthquakes[J]. Bull Seism Soc Amer, 64(2): 393-414.
-
期刊类型引用(16)
1. 何贵阳,周菊玲. Mlinex损失函数下反向帕累托分布形状参数的Bayes估计. 新疆师范大学学报(自然科学版). 2024(01): 1-12 .  百度学术
百度学术
2. 赵宜宾,王福昌,任晴晴,张艳芳,钱小仕. 基于广义极值分布的巴颜喀拉块体中部地震危险性分析. 世界地震工程. 2023(01): 209-217 .  百度学术
百度学术
3. 张艳芳,赵宜宾,任晴晴. 广义Pareto分布参数的Bootstrap置信区间及应用. 工程数学学报. 2023(06): 1011-1020 .  百度学术
百度学术
4. 程磊,陆蔺,卜树坡. 基于运行误差估算的电能表准确性预计. 电测与仪表. 2022(04): 49-54 .  百度学术
百度学术
5. 黄一凡,孟生旺. 中国地震指数保险设计与定价研究. 统计研究. 2022(04): 108-121 .  百度学术
百度学术
6. 赵宜宾,王福昌,任晴晴,张艳芳,钱小仕. 基于广义极值分布的东昆仑山断裂带周边区域地震危险性分析. 防灾科技学院学报. 2022(02): 82-89 .  百度学术
百度学术
7. 任晴晴,赵宜宾,钱小仕,李科长,张艳芳. 基于POT模型的昆仑山地区地震统计特征分析. 震灾防御技术. 2022(03): 529-538 .  百度学术
百度学术
8. 赵宜宾,张艳芳,王福昌,任晴晴. 基于轮廓似然估计的广义极值分布在地震中长期预测中的应用. 地震学报. 2022(06): 1061-1071 .  本站查看
本站查看
9. 任梦依,刘哲. 青藏高原东北缘地震活动性广义帕累托模型的全域敏感性分析. 地震学报. 2022(06): 1035-1048 .  本站查看
本站查看
10. 周宁馨,刘青,查虹丽,马龙雄. 地磁场极值预测及磁暴感应地电场有限元计算. 智慧电力. 2021(03): 88-94 .  百度学术
百度学术
11. 周宁馨,刘青,查虹丽,马龙雄. 基于广义帕累托分布的中纬度地区地磁场极值预测. 西安科技大学学报. 2021(03): 524-530 .  百度学术
百度学术
12. 于群,刘启林. 广义Pareto分布在南方电网大停电事故分析中的应用. 数学的实践与认识. 2020(19): 175-185 .  百度学术
百度学术
13. 田建伟,刘哲,任鲁川. 基于广义帕累托分布的马尼拉海沟俯冲带地震危险性估计. 地震. 2017(01): 158-165 .  百度学术
百度学术
14. 任杰,苏怀智,吴邦彬,朱茜,赵斌. 基于极值理论的岩质边坡变形预警指标估计. 水电能源科学. 2016(03): 145-147+139 .  百度学术
百度学术
15. 任杰,苏怀智,陈兰,许焱鑫. 基于POT模型的大坝位移预警指标实时估计. 水力发电. 2016(04): 45-48 .  百度学术
百度学术
16. 任杰,苏怀智,杨孟,周志杰. 边坡位移预警指标的实时估计与诊断. 水利水运工程学报. 2016(01): 30-36 .  百度学术
百度学术
其他类型引用(8)




 下载:
下载: