3D scattering by an alluvial valley embedded in a layered half-space for obliquely incident Rayleigh waves
-
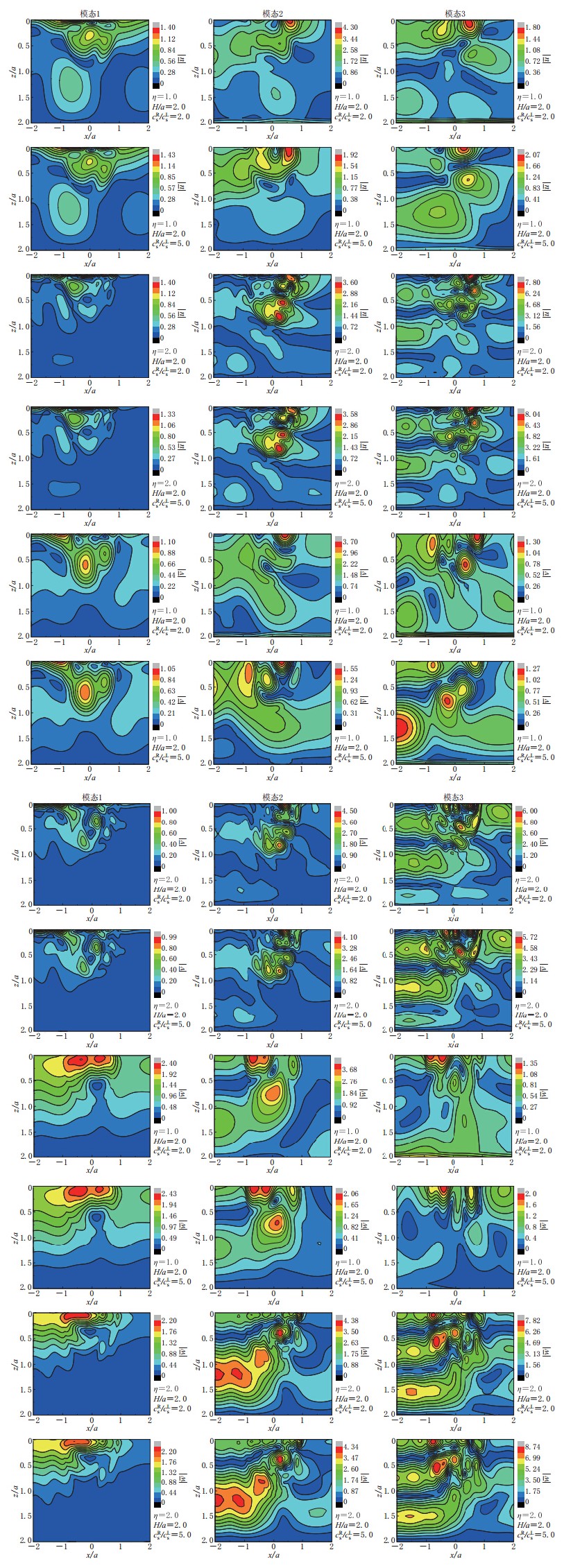
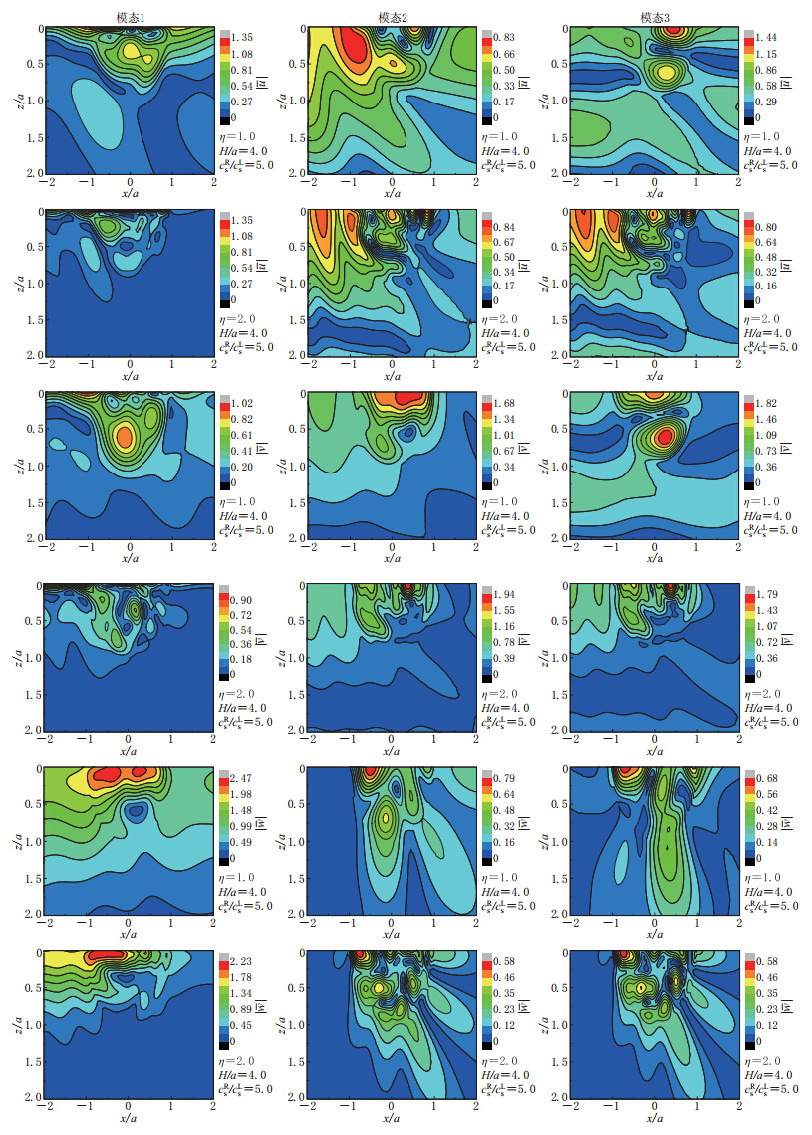
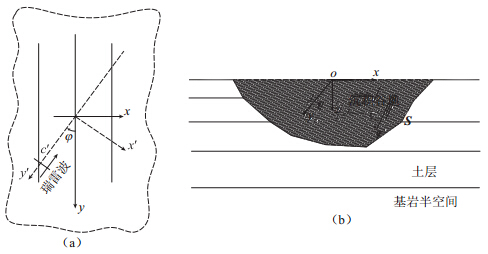
摘要: 针对层状半空间中沉积谷地对斜入射瑞雷波的三维散射问题， 采用直接刚度法计算自由场波场， 以层状半空间中移动斜线均布荷载动力格林影响函数求解三维散射波场， 建立了求解该问题的间接边界元方法. 通过与已有结果的比较， 验证了该方法的正确性， 并以均匀半空间以及弹性基岩上单一土层场地中沉积谷地为例进行了计算分析. 研究结果表明： 层状半空间与均匀半空间中沉积谷地对瑞雷波的散射存在显著差别； 层状半空间中瑞雷波的振动模态对沉积附近位移幅值有着重要影响； 土层刚度和厚度等参数也对沉积附近位移幅值大小及空间分布有着显著的影响.Abstract: Aiming at solving the problem of 3D scattering by an alluvial valley embedded in a layered half-space, the indirect boundary element method (IBEM) is established based on the free wave field calculated by using the direct stiffness method, and 3D scattering wave field simulated by using the Green’s functions of moving distributed loads in the layered half-space. The method is validated by comparison with known results, and numerical analyses are performed by examples of a valley embedded in a uniform half-space and in a single soil layer over elastic bedrock. The results show that the wave scattering around the valley embedded in a uniform half-pace are distinctively different from that in a layered half-space, the modals of the Rayleigh waves in a layered half-space have important effects on the displacement amplitudes around the valley, and also the stiffness and depth of the soil layer have important influence on the amplitudes and distribution of the displacement.
-
Keywords:
- 3D scattering /
- alluvial valley /
- Rayleigh wave /
- moving Green’s function /
- layered half-space
-
-
![]()
图 1 计算模型
(a) 瑞雷波入射方位图； (b) 沉积谷地截面图
Figure 1. Calculation model
(a) Azimuth of incident Rayleigh wave； (b) Cross section of the alluvial valley
![]()
图 2 本文计算结果与Dravinski和Mossessian (1987)结果的比较
Figure 2. Comparison of results given by the present method with those by Dravinski and Mossessian (1987)
![]()
图 3 水平入射角度φ不同时沉积谷地附近地表位移幅值
Figure 3. Displacement amplitudes around the alluvial valley for different horizontal incident angles
![]()
图 4 水平入射角度不同时沉积谷地附近位移幅值云图
Figure 4. Contours of displacement amplitudes near the alluvial vally for different horizontal incident angles φ
![]()
图 5 层状半空间基岩单一土层场地频散曲线
Figure 5. Dispersion curves of a single soil layer overlaid on bedrock in half-space
![]()
图 6 沉积谷地附近位移幅值云图(场地1和场地2)
Figure 6. Contours of displacement amplitudes around the alluvial valley (site 1 and site 2)
-
巴振宁. 2008. 层状半空间中格林函数和局部场地对弹性波的散射[D]. 天津: 天津大学土木工程系: 72-77. Ba Z N. 2008. Green's Functions for Layered Half Space and Elastic Wave Scattering by Local Sites[D]. Tianjin: Department of Civil Engineering, Tianjin University: 72-77 (in Chinese).
巴振宁, 梁建文. 2012. 层状场地中二维沉积谷地对弹性波的三维散射[J].土木工程学报, 45(S1): 146-151. Ba Z N, Liang J W. 2012. Three-dimensional scattering by a two-dimensional valley embedded in a layered half-space[J]. China Civil Engineering Journal, 45(S1): 146-151 (in Chinese).
梁建文, 张秋红, 李方杰. 2006 . 浅圆沉积谷地对瑞雷波的散射: 高频解[J]. 地震学报, 28(2): 176-182. Liang J W, Zhang Q H, Li F J. 2006. Scattering of Rayleigh waves by a shallow circular alluvial valley: High-frequency solution[J]. Acta Seismologica Sinica, 28(2): 176-182 (in Chinese).
梁建文, 巴振宁. 2007a. 弹性层状半空间中沉积谷地对入射平面SH波的放大作用[J]. 地震工程与工程振动, 27(3): 1-9. Liang J W, Ba Z N. 2007a.Surface motion of an alluvial valley in layered half-space for incident plane SH waves[J]. Journal of Earthquake Engineering and Engineering Vibration, 27(3): 1-9 (in Chinese).
梁建文, 巴振宁. 2007b. 三维层状场地的精确动力刚度矩阵及格林函数[J].地震工程与工程振动, 27(5): 7-11. Liang J W, Ba Z N. 2007b. Exact dynamic stiffness matrices of 3-D layered site and its Green's functions[J]. Journal of Earthquake Engineering and Engineering Vibration, 27(5): 7-11 (in Chinese).
梁建文, 魏新磊, Lee V W. 2009. 圆弧形沉积谷地对Rayleigh波三维散射解析解[J]. 天津大学学报, 42(1): 1345-1353. Liang J W, Wei X L, Lee V W. 2009. Analytical solution for 3D scattering of Rayleigh waves by a circular-arc alluvial valley[J]. Journal of Tianjin University, 42(1): 1345-1353 (in Chinese).
首培烋, 刘曾武, 朱镜清. 1982. 地震波在工程中的应用[M]. 北京: 地震出版社: 56-59. Shou P X, Liu Z W, Zhu J Q. 1982. The Application of Seismic Wave in Engineering[M]. Beijing: Seismological Press: 56-59 (in Chinese).
王海云. 2011. 渭河盆地中土层场地对地震动的放大作用[J]. 地球物理学报, 54(1): 137-150. Wang H Y. 2011. Amplification effects of soil sites on ground motion in the Weihe basin[J]. Chinese Journal of Geophysics, 54(1): 137-150 (in Chinese).
张郁山. 2010. 圆弧状多层沉积谷地在Rayleigh波入射下动力响应的解析解[J]. 地球物理学报, 53(9): 2129-2143. Zhang Y S. 2010. Analytical solution to dynamic response of circular arc-shaped multi-layered valley due to incidence of Rayleigh wave[J]. Chinese Journal of Geophysics, 53(9): 2129-2143 (in Chinese).
赵成刚, 王磊, 高福平. 2007. 圆弧形沉积场地对平面瑞利波散射的解析分析[J]. 力学学报, 39(3): 365-373. Zhao C G, Wang L, Gao F P. 2007. Scattering of plane Rayleigh waves by a circular-arc alluvial valley: An analytical solution[J]. Chinese Journal of Theoretical and Applied Mechanics, 39(3): 365-373 (in Chinese).
De Barros F C P, Luco J E. 1995. Amplification of obliquely incident waves by a cylindrical valley embedded in a layered half-space[J]. Soil Dyn Earthq Engng, 14: 163-175.
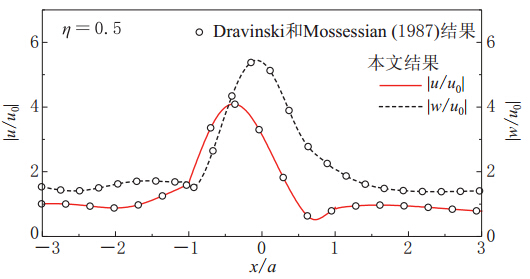
Dravinski M, Mossessian T K. 1987. Scattering of plane harmonic P, SV, and Rayleigh waves by dipping layers of arbitrary shape[J]. Bull Seismol Soc Am, 77(1): 212-235.
Kawase H, Aki K. 1989. A study on the response of a soft basin for incident S, P and Rayleigh waves with special reference to the long duration observed in Mexico city[J]. Bull Seismol Soc Am, 79(5): 1361-1382.
Pedersen H, Sánchez-Sesma F J, Campillo M. 1994. Three-dimensional scattering by two-dimensional topographies[J]. Bull Seismol Soc Am, 84(4): 1169-1183.
Sánchez-Sesma F J, Ramos-Martinez J, Campillo M. 1993. An indirect boundary element method applied to simulate the seismic response of alluvial valleys for incident P, S and Rayleigh waves[J]. Earthq Eng Eng Vib, 22(4): 279-295.
Todorovska M I, Lee V W. 1990. A note on response of shallow circular valleys to Rayleigh waves: Analytical approach [J]. Earthq Eng Eng Vib, 10(1): 21-34.
Wolf J P. 1985. Dynamic Soil-Structure Interaction[M]. Englewood Cliffs: Prentice-Hall: 322-325.
下载:
计量
- 文章访问数: 545
- HTML全文浏览量: 211
- PDF下载量: 12
