Weighted two-step regression method of attenuation relationship considering sample uneven distribution
-
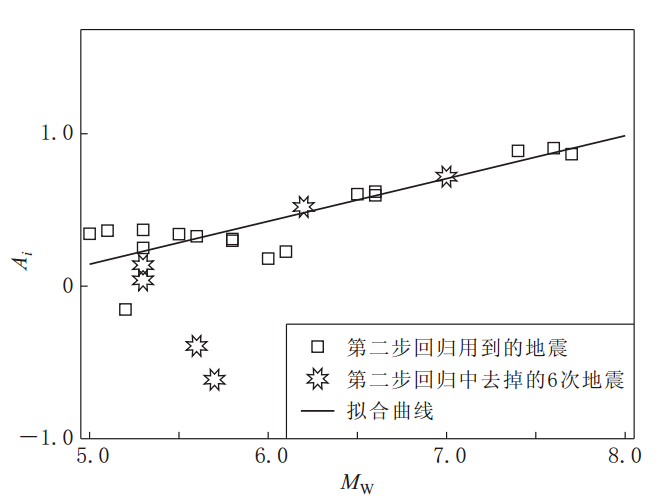
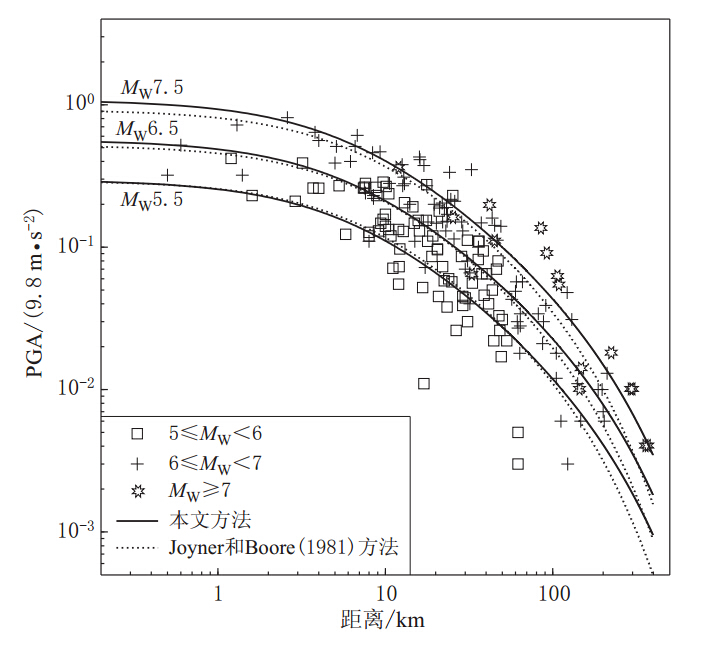
摘要: 通过对距离和震级的分档将权重引入两步回归法: 第一步， 将地震记录按距离分档， 每个记录得到的权重为w'ij=1/(njni)(其中nj为该记录所在档的地震数， ni为该记录的地震在此档中的记录数)， 这种权重的取法不仅使各档的权重相同， 而且保证每档中不同地震在各档中的权重也相同； 第二步， 将地震按震级分档， 每次地震得到的权重为v'k=1/nk(其中nk为该地震所在档的地震数). 以Joyner 和Boore的数据为分析对象进行加权两步法的回归， 并与传统两步法回归的结果进行比较. 结果表明: 传统两步法在近场拟合的小震峰值加速度的估计值偏大， 大震峰值加速度的估计值偏小， 其衰减曲线在远场的衰减速度过快； 而加权两步法则能更好地反映地震动的空间分布规律.Abstract: Weight is introduced into two-step method by grading distances and magnitude. In the first step, the recordings are divided into several intervals by range of distances. Every recording gets one weight w'ij=1/(njni) (nj is the number of earthquakes in the interval in which the recording is located, ni is the number of recordings of the earthquake in this interval). Not only does the way of getting weight keep equal weight for every interval, but also promises the same weight for earthquakes in any interval. In the second step, the earthquakes are divided into several intervals by range of magnitudes. Every earthquake get one weight v'k=1/nk (nk is the number of earthquakes in the interval in which the earthquake is located). Taking the recordings used by Joyner and Boore (1981) as instance, comparing results from weighted two-step method with that from traditional one, the results show that values of peak ground acceleration (PGA) in near sites fitted by traditional method are higher than that fitted by weighted method for small events and lower for large events, attenuating rates are much rapider in far sites; weighted two-step method is better to simulate spatial distribution laws of ground motions than traditional method.
-
Keywords:
- weight /
- two-step method /
- peak ground acceleration /
- distribution law
-
-
![]()
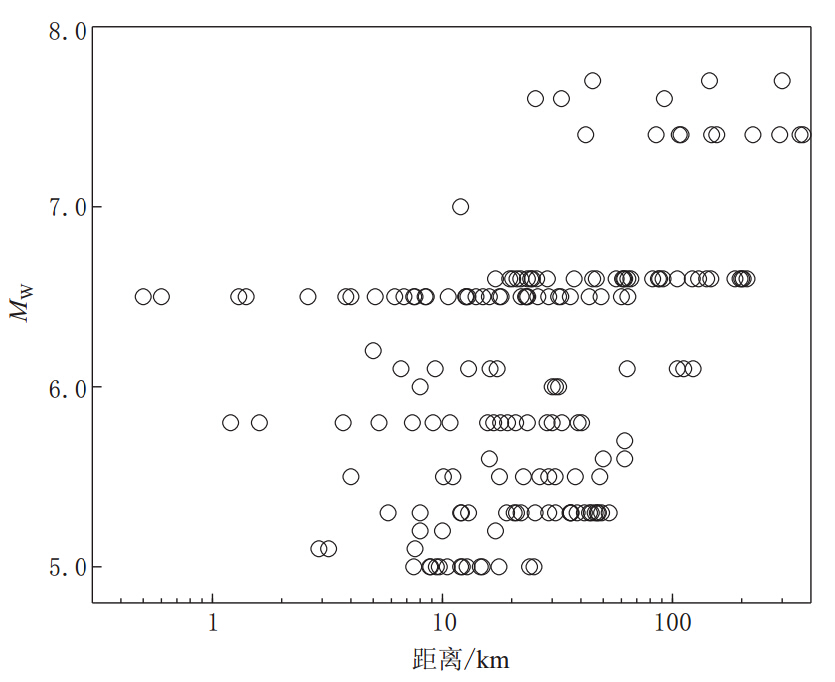
图 1 峰值加速度记录的震级与距离分布图
(修改自Joyner，Boore，1981)
Figure 1. Distribution of PGA recordings with respect to magnitude and distance
(modified after Joyner，Boore，1981)
![]()
图 2 Ai-MW关系图
The blocks represent the events in the second step regression, the stars represent the six events not involved in the second step regression, the straight line represents the fitted curve
Figure 2. Values of Ai against magnitude MW
![]()
图 3 传统两步法与加权两步法拟合衰减曲线比较及散点分布图
Figure 3. Comparison of attenuation curves by traditional two-step method and weighted two-step method with scatter diagram
表 1 用于回归分析的地震及记录数
Table 1 Earthquakes used for regression analyses and number of recordings
下载: 导出CSV
-
霍俊荣, 胡聿贤. 1992. 地震动峰值参数衰减规律研究[J]. 地震工程与工程振动, 12 (1): 1-11. Huo J R, Hu Y X. 1992. Study on attenuation laws of ground motion parameters[J]. Earthquake Engineering and Engineering Vibration, 12 (1): 1-11 (in Chinese).
卢建旗, 李山有, 李伟. 2009. 改进的两步法在地震动衰减关系建立中的应用[J]. 世界地震工程, 25 (3): 46-48. Lu J Q, Li S Y, Li W. 2009. Application of improved two-step method on establishment of ground motion attenuation relationship[J]. World Earthquake Engineering, 25 (3): 46-48 (in Chinese).
王国新, 陶夏新. 2001. 地震动衰减关系拟合的新两步法[J]. 地震工程与工程振动, 20 (1): 24-28. Wang G X, Tao X X. 2001. A new two-steps method for fitting ground motion attenuation relationship[J]. Earthquake Engineering and Engineering Vibration, 20 (1): 24-28 (in Chinese).
肖亮, 俞言祥. 2010. 一种新的拟合地震动衰减关系的分步回归法[J]. 地震学报, 32 (6): 725-732. Xiao L, Yu Y X. 2010. A new step-regression approach for fitting ground motion data with attenuation relation[J]. Acta Seismologica Sinica, 32 (6): 725-732 (in Chinese).
Campbell K W. 1981. Near-source attenuation of peak horizontal acceleration[J]. Bull Seismol Soc Am, 71 (6): 2039 -2070.
Draper N R, Smith H. 1998. Applied Regression Analysis[M]. 3rd edition. New York: John Wiley & Sons, Inc. : 507-511.
Joyner W B, Boore D M. 1981. Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 Imperial Valley, California, earthquake[J]. Bull Seismol Soc Am, 71 (6): 2011-2038.
计量
- 文章访问数: 556
- HTML全文浏览量: 258
- PDF下载量: 24
