引言

地震定位一直是地震学最经典、最基本、最核心的问题之一，对于研究诸如地震活动构造、地球内部结构、震源几何结构等地震学问题具有重要意义．然而，对这一理论上具有唯一性的问题，各研究机构、团队或个人给出的结果却不尽相同，甚至差异较大．其原因除与所用计算方法有关外，还与选取的速度模型、所用台站数量、台站震中距和方位角分布、震相读取的精度、震后快速响应发布结果时所能获取的第一手资料等诸多因素有关．

地震定位方法种类繁多，从大的方面讲，可分为线性和非线性两种．其基本原理都是求取某一目标函数的极小值，且各种方法均有其适用范围和局限性．田玥(2001)曾对Inglada(1928)提出的线性单事件近震定位方法的求解进行了一定的改进，但仍要求所有参与定位的台站均具有较为准确的P波和S波到时数据．这一要求在实际定位工作中限制了其适用范围，且田玥(2001)只进行了理论验证和误差分析讨论，并未给出具体的应用实例．众所周知，对于诸如2008年汶川M_S8.0地震这样的巨大地震事件，甚至大多数6—7级以上地震(如芦山M_S7.0地震)，其近场记录因限幅、仪器移位或损坏等原因，往往只有P波初始部分能被清晰地记录下来(强震仪虽有完整记录，但S波震相不易拾取，数据及时性也有问题)，S波到时往往难以全部准确获取．因此，本文试图在前人研究的基础上，结合日常地震快速定位和地震早期预警中只有P波到时容易且能准确、快速获取这一事实，对线性单事件定位方法进行局部改进，使其更切合近源定位情形．

对地震尤其是7级以上大地震的三要素而言，大孔径台网诸如国家台网、全球台网在震级确定，特别是面波震级、矩震级等的确定方面具有更高的权威性．然而，由于受制于地球介质横向和垂向的不均匀性，大孔径台网(如CENC)所给出的震源时空参数往往不如小孔径的区域台网精准，张晁军等(2010)对此进行了专门的研究．

鉴于此，本文尽可能利用距离汶川M_S8.0地震震中最近的各种台站资料，结合修改后的近震定位程序来尝试修正该地震的时空参数．所用台站的震中距均在30 km以内，其中紫坪铺水库台网的八角台，震中距小于5 km，符合对精确计算震源深度误差的特别要求(张晁军等，2010)．

1.   线性单事件定位法

1.1   方法原理

This page contains the following errors:

Below is a rendering of the page up to the first error.

对于台站i，

对于台站j，

将式(2)和式(3)展开后相减，消去二次项，得到线性方程

其中r²_i=x²_i+y²_i+z²_i．

将式(4)用于4个以上的台站，利用全部台站对，即可得到一个关于(x₀，y₀，z₀)的线性方程组．由于台站i与j的海拔高差|z_i-z_j|的数量级远小于经向距离差|x_i-x_j|和纬向距离差|y_i-y_j|，所以此线性方程组系数矩阵有奇异性，导致z₀解发散，故首先须利用奇异值分解法从方程组计算得到震源位置(x₀，y₀)，再利用式(2)和

取各台平均值求得相对独立且互相解耦的震源深度z₀和发震时刻值t₀．

1.2   方法改进

上述线性单事件定位方法巧妙地将非线性方程组求解问题简化为线性方程组的求解，其原理简单，且不需给出初值，不用迭代，可以直接求解，因而能够较好地用于近震定位研究中．然而相对矛盾的是，对于近震而言，特别是6级以上地震往往只能获得高质量的P波记录，S波震相到时由于限幅、仪器移位等诸多因素不能确保全部获得．无论从地震速报的常规定位还是从地震快速预警实际需求来讲，近震P波初动到时由于清晰可辨，容易在第一时间准确、快速获取，且精度较高； 而S波到时由于机器自动识别困难，人工读取往往与个人经验有关，因此常常因人而异，其识别误差要比P波到时大很多．其次，地壳中的P波速度模型也比S波速度模型更为精准．如果只用P波到时和P波速度即可快速定位，其适用范围、时效性和精准性将大大提高．因此，本文对上述线性单事件定位方法进行了适当的改进，使其能应用于需要快速响应或记录不完整的近源强震定位，而且只需4个以上(含4个)台站的P波初动到时即可给出具有相当精度的线性定位结果．

同样依据上述原理，对于台站i来讲，显然有t_Pi-t₀=R_i/v_P，从而

对于台站i，

对于台站j，

将式(7)和式(8)展开后相减，消去二次项，得到线性方程

其中r²_i=x²_i+y²_i+z²_i．将式(9)用于4个以上台站的全部台站对，即可得到一个关于(x₀，y₀，z₀，t₀)的线性方程组，从而可同时计算得到震源位置和发震时刻．

同样地，由于 z_i 表示台站i的海拔高程(或安装深度)，而实际台站对海拔高差|z_i-z_j| 的数量级仅为米级，远小于台站对的经向距离差|x_i-x_j|、纬向距离差|y_i-y_j|和|v²_P(t_Pj- t_Pi)|(一般为千米级)．即使像龙门山地区这样东西两侧海拔高程差异较大的地区，根据台站对所列方程组系数矩阵的最大与最小奇异值之比也能达10³量级，这使得式(9)的系数矩阵具有明显的奇异性，导致z₀解发散，甚至会给出不可能的解．为此，我们通过一种简单方法单独求解z₀，将式(9)移项后得到

先假定z₀ =0(即表面源假定，实际上由于台站对的高程差|z_i-z_j|较水平向距离差小3个左右数量级，对震中和发震时刻的求解结果影响非常小，相当于略去式(10)右边最后一项)，得震中和发震时刻初解(x′ ₀，y′ ₀，t′ ₀)，将其代入式(7)求得z′_0i，然后将各个台站求得的z′_0i取平均值作为震源深度的初解再次代入式(10)，如此反复直至z₀保持不变为止(一般计算3—5次即可)，这样即可求得平均意义上的震源深度值和较为稳定的震中位置及发震时刻解(x₀，y₀，t₀)，同时使发震时刻与震源深度相对解耦．

本方法的好处还在于，如果平均速度随深度改变(如分层均匀模型)，则可将深度与平均速度关系引入上述迭代过程同时修改，从而得到深度和平均速度能够自洽的震中位置和发震时刻(x₀，y₀，t₀)．而z₀的误差仅取决于震中位置和发震时刻的定位误差、P波到时读取误差和平均P波速度(三者均是可控的，因为主要为走时读取的误差)，这样即从根本上解决了方程组本身无法有效求解震源深度的难题．实际计算表明，以式(10)所列方程组左边的系数矩阵不存在奇异性，因而解法非常简单，可采用方程组系数矩阵的广义逆直接左除方程组的右边求解，无需考虑奇异值分解等难题．

通过作上述适当改进，既保证了方程组的线性特征，又能同时求出发震时刻，且只需获得4个以上台站的P波初动到时和P波平均速度即可定位．实际求解中则可利用尽可能多的台站数据，并使用全部的台站对，会得到较好的定位结果．

2.   理论检验及其与Geiger法比较

2.1   单层均匀速度模型检验

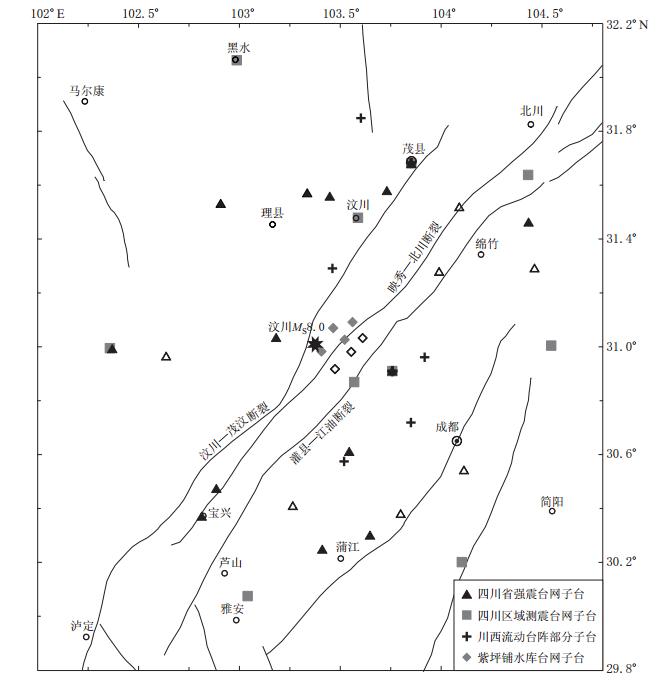
为了与实例应用相一致，我们取汶川地震科学考察队给出的汶川M_S8.0地震的时空参数作为理论震源时空参数，以震中周围实际分布并可获得准确P波到时的四川省强震台网、四川区域测震台网、川西流动台阵、紫坪铺水库台网等共计31个距离震中120 km范围内(首波出现可能性不大，确保第一震相为直达P波)实际分布的台站作为理论检验台站(图1)，单层均匀P波速度取5.64 km/s．首先根据理论参数和模型正演计算出各台的P波理论到时，再根据各台P波理论到时数据分别采用本文提出的线性单事件定位改进方法与Geiger方法(取P波到时最小的台站经纬度、P波到时和震源深度h=10 km为初值)进行计算．

图  1  龙门山地区区域构造、所用台站及其空间分布图 图中各种空心符号代表虽有台站，但其时间服务有明显错误或GPS故障子台，本文中其时间资料均未被采用

Figure  1.  Regional tectonic background and distribution of strong motion stations(black triangle)，broad-b and stations(grey square)，mobile stations(black cross) and reservoir seismic stations(diamond)in Longmenshan area. Hollow symbols indicate the stations that time service is bad. Black star is the epicenter of Wenchuan M_S8.0 earthquake given by this paper

下载: 全尺寸图片 幻灯片

考虑到实际定位过程中的P波到时读取可能会存在一定的误差，其原因一方面是由于时间服务精度(如采样率)造成的，另一方面则是人为读取所致； 因此我们对计算的各台站理论时间进行了精度取舍，分别只取小数点后4位(实验1)、小数点后2位(实验2)、小数点后1位(实验3)和小数点后两位但需加上最大为±0.20 s的随机误差(实验4)，以此检验两种方法的容错性．从表1的理论检验结果不难看出，本文方法与Geiger法均能取得较为精确的结果．进一步比较表明，实验1和实验2由于有较为精确的时间读数，在发震时刻和震中位置上两种方法均给出了较高精度解，但在深度上本文方法误差略小于Geiger法； 当时间读数存在一定人为误差时(如实验3和实验4)，本文方法得到的震中位置误差略小，而发震时刻和震源深度的误差却略大于Geiger法结果. 而采用两种方法得到的发震时刻误差均小于0.05 s，震中位置误差均小于0.15 km，震源深度误差均不超过1 km．也即在最大人为误差≤0.2 s(通常近震P波到时远小于此量级)的情况下，所得结果具有足够的精度，具备了良好的容错性．理论实验证明，本文的改进方法对单层均匀模型足以给出较为精确的结果．如果P波到时足够精准(如实验2)，震源深度的结果甚至还略优于Geiger法，Geiger法需设定初值，而本文方法则无此限制，因此具有一定的优越性．

表  1  文方法与Geiger法在单层均匀速度模型中理论检验结果的比较(全部31台)

Table  1.  Comparison of theoretical test results between the improved linear method in this paper and the Geiger method for single event seismic location in a single-layer

下载: 导出CSV 

| 显示表格

2.2   龙门山地区分层均匀速度模型实验

从上述理论检验可以看出，对于单层均匀速度模型假设，本文改进的方法无疑是一种既简单快捷(无初值依赖，只需P波初动到时即可)又较为准确实用的线性单事件定位方法．需要指出的是，单层均匀速度模型假设作为极为复杂而又不易获取的精确地下结构的一级近似，在大多数情况下还是简单适用的，特别是在无法获取较为精确速度模型的地区以及在精度要求不高或需要快速粗略估计(如地震预警)的情况下，该假设仍然有其明显的实际需求，特别是单层均匀模型所定出的经纬度坐标与分层均匀模型结果差异并不大．但对于像龙门山这样已经有很精细速度模型(赵珠等，1997； 黄媛等，2008)的地区而言就显得有些不合时宜了．如何将基于单层均匀速度模型理论的线性单事件定位方法在一定条件下推广应用于分层均匀速度模型，以及该推广在何种情况下可用，何种情况下不再适用，我们就此问题进行了理论实验．

将改进的线性单事件定位方法应用于分层均匀模型，实际上就是如何将分层均匀速度模型转换(或折合)为单层均匀模型．当然，精确的转换是不可能的，这里面临两个难题： 其一，分层均匀介质中，平均(或折合平均)地震波速实际上可表示为v(h，Δ)或v(h，i_k)，是与震源深度和震中距(或离源角i_k)有关的函数，而随着震源深度不同，平均波速(震源距除以总时间)已不同； 其二，地震射线也由单层均匀介质中的直线变成了具有多个折点的折线．如果参与定位的台网各台站距离震中足够近(如30—60 km内)，平均波速则随震中距变化不大，且地震射线也可近似为直线，此时我们可采取一定的简化假设，忽略震中距(或离源角)不同而导致的平均速度差异(即不考虑震中距的影响)，直接根据分层均匀速度模型将与震源深度对应的折合平均速度

作为单层均匀速度模型的近似速度值代入式(10)，与h(h已知即可变换得到v_P)一起迭代求解．

利用与上述单层均匀速度模型试验相同的理论参数，根据赵珠等(1997)给出的龙门山地区分层均匀速度模型(表2)，我们进行了理论验算，其结果分别列于表3(假设h=18.66 km)和表4(假设h=9.50 km)．从表3和表4两种不同深度的理论测试实验中可以看出: 将改进后的线性单事件定位方法从单层均匀速度模型尝试推广至分层均匀速度模型时，随着台网最大震中距的缩小(相应台站数目减少)，震中位置和震源深度误差均越来越小，定位结果越来越接近理论值； 发震时刻的变化则有些复杂，虽然其总体也呈误差逐渐减小趋势，但当震源深度较浅(表4)时，误差起伏波动则较大，直到最大震中距在40 km以内才与震中位置和深度误差同步减小．进一步比较还可看出： 当台网孔径较大时(如31个台站，最大震中距为114 km)，所得结果中震中位置误差并不大(经、纬度都是小数点后第3位变化，震中位置误差小于1 km)，表明震中位置(经度和纬度)与速度误差基本上是解耦的； 但发震时刻和震源深度误差很大(表3和表4中时间差分别为0.43 s和0.38 s，深度差分别为4.88 km和7.80 km)，显示与平均速度精度高度相关，且彼此仍然无法完全解耦，均呈此消(深度减小)彼长(时间增加)的变化．

表  2  龙门山断裂带的4种P波平均速度模型

Table  2.  Four P-wave velocity models in Longmenshan fault zone

下载: 导出CSV 

| 显示表格

表  3  本文方法在分层均匀速度模型中的理论检验结果(h=18.66 km)

Table  3.  Theoretical test result of the improved linear method in this paper for single event seismic location in a layered homogenous crust model(h=18.66 km)

下载: 导出CSV 

| 显示表格

表  4  本文方法在分层均匀速度模型中的理论检验结果(h=9.50 km)

Table  4.  Theoretical test result of the improved linear method in this paper for single event seismic location in a layered homogenous crust model(h=9.50 km)

下载: 导出CSV 

| 显示表格

2.3   理论误差分析与适用范围界定

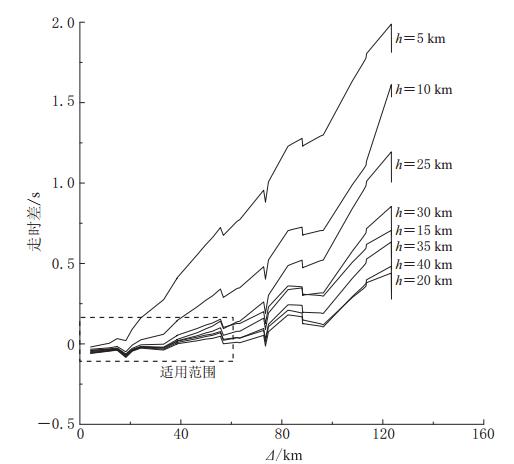
从上述理论检验可以看出，由于只是一种近似折合，随着所用最远台站震中距变小(相应台站数减少)，空间位置变化不大，而发震时刻和震源深度逐渐接近理论值，体现为计算深度与理论深度及计算发震时刻与理论发震时间的误差均逐步减小．因此可以肯定，单层均匀模型假设可以应用于当台站足够靠近震中时的均匀分层速度模型近似．那么这个距离范围大概是多少呢？ 为此我们沿用赵珠等(1997)给出的龙门山地区常用速度模型和周围实有台站参数，理论计算了同一地震从分层均匀速度模型及折合单层均匀速度模型(根据深度相应变化)到各台站的理论走时差，并分析了其与震源深度和震中距的关系，结果如图2所示．可以看出，两种走时差与震源深度的关系极为复杂，但总体上呈深度越浅，则误差越大的趋势．特别是当震源深度小于10 km时，走时差似乎随震中距呈指数增长. 而无论何种震源深度，走时差随震中距的增加而增加的关系比较明显．若取二者走时差在±0.2 s内(见表1中的容错性实验4)为容许范围，则该假设的适用范围应该在60 km以内较为合适(图2虚线框所示范围)．当震源深度小于10 km时，所用台站应该更近，最好在30 km以内．

图  2  分层均匀速度模型与折合单层均匀速度模型理论走时差与震源深度h、台站震中距Δ、台站海拔高程的关系(图中拐点为实际台站海拔高程影响)

Figure  2.  Theoretical travel time difference between the layered homogeneous velocity model and its approximate single-layer homogenous velocity model related to focal depth h，epicentral distance Δ，and elevation of stations(see the inflexions of the curves)

下载: 全尺寸图片 幻灯片

3.   实例应用

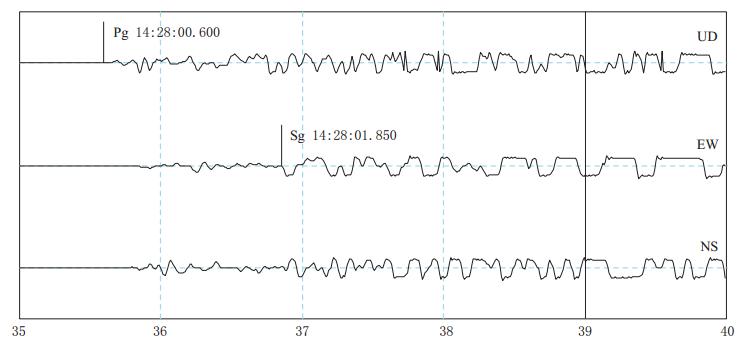
汶川M_S8.0特大地震虽然已过去了6年多，但对该地震的研究却从未停止过．不同的研究机构及团队(黄媛等，2008； 吕坚等，2008； 陈九辉等，2009； 中国地震局监测预报司，2009； 杨智娴等，2012； 张新东等，2013)对汶川地震的主震参数分别给出了不同的结果，如表5所示．中国地震台网中心(CENC)也对其给出的地震参数进行了多次修正，并在《汶川8.0级地震科学研究报告》(中国地震局监测预报司，2009)中给出了最终结果．然而，本文作者在处理强震记录的时间资料时，却发现像汶川卧龙台这样近距离台站高质量的初至到时表明，CENC给出的发震时刻几乎是不可能的．这一点也被川西流动地震台阵近距离观测台KCD05的初至到时(刘启元等，2008)及四川省区域测震台网油榨坪台和紫坪铺水库台网八角台的记录(图3)所证实．刘启元等(2008)提出应对汶川主震的时间参数进行修正，其后中国地震局汶川科学考察队利用川西流动台网资料公布了其给出的时空参数的修正结果(表5)，但未能在CENC的最终新参数(中国地震局监测预报司，2009)中得以反映．上述结果中由于所用台站震中距均大于20 km，虽有精细的速度模型或非线性方法，但所得结果由于不满足精确确定震源深度所必需的近源台站到时(张晁军等，2010)，因而震源深度值的准确性仍然有待商榷．杨智娴等(201 2)利用Geiger法将紫坪铺水库台网资料补充进四川区域台网，给出了重新修定的汶川地震的时空参数．所用台站虽然有较好的方位角分布，但震中距依然为5—160 km. 虽然程序给出的定位误差不大，但是由于使用了远距离台站，加大了地壳结构横向不均匀性的影响，导致震源深度和发震时刻的耦合仍然折衷(trade-off)明显．显然，如果主震的发震时刻和深度均有问题，则其它震源参数也有必要重新修正．

图  3  距离震中最近的紫坪铺水库台网八角(BAJ)台记录的汶川M_S8.0三分量地震波形及其P波初至(Pg)和S波初至(Sg)到时

Figure  3.  The three-component seismogram and arrival times of Pg and Sg of Wenchuan M_S8.0 earthquake recorded at the nearest station BAJ of Zipingpu reservoir seismic network

下载: 全尺寸图片 幻灯片

表  5  不同研究机构及团队给出的汶川M_S8.0主震震源参数

Table  5.  Focal parameters of Wenchuan M_S8.0 main shock given by different institutions and authors

下载: 导出CSV 

| 显示表格

从上述理论分析和检验可知，当本文的改进方法应用于分层均匀模型时，为获得可靠的结果，尽可能选取震中距较小且满足定位要求的台网资料. 因此，我们选取震中距在30 km范围内仅有的5个台站(其中4个为紫坪铺水库台，1个为汶川卧龙强震台)的P波初动到时，依据本文的折合均匀单层速度模型方法，分别利用杨智娴等(2012)、黄媛等(2008)西区和东区及赵珠等(1997)所给的龙门山地区模型计算汶川主震事件的时空参数，并与使用相同模型的Geiger法结果相比较(表6，表7). 结果表明： ① 由4种不同模型折合出来的平均P波速度为5.15—5.81 km/s(相差0.66 km/s)，差异较大，但不同模型给出的震中位置吻合较好，差异仅在小数点后第三位，即小于1 km. 而不同模型给出的震源 深度和发震时刻则差异明显，震源深度从11.41—8.28 km不等，发震时刻从58.10—58.87 s 不等．可以看出： 在台网不变时，震中位置与速度模型基本解耦，震深源度和发震时刻受速度模型影响较大，且二者并未完全解耦，呈此消彼长现象； 但不同模型给出的震源深度均比前人给出的偏小，集中于8.0—11.5 km．② 本文改进方法与Geiger单层均匀模型方法在速度一致的情况下，所得结果基本一致，但震源深度和发震时刻的系统差分别约为0.3 km和0.02 s，主要源于一个用最小二乘法，一个直接求平均，但误差量级相当．此外，由两种方法得到的经度值非常接近(小数点后4位差异)； 对纬度而言，Geiger法比本文方法系统偏小(小数点后3位差异)，本文方法得到的纬度值较Geiger法稳定，也说明Geiger法与台站的方位角展布关系更为密切．③ 表7详细列出了基于不同模型利用不同方法定位结果计算的各台理论走时与观测走时残差及相应的方均根误差．可以看出，最大残差均不超过0.2 s，5个台中有4个台的残差均小于0.1 s. 依据表1中实验4的检验结果，说明折合模型所得结果的精度是符合实际定位要求的．只从残差看，难于区分各种模型和方法的优劣，但从相应的方均根误差来看，Geiger法比本文改进方法略好(误差小0.01左右). 此外，相比其它模型，黄媛等(2008)西区模型方均根误差最小，且从5个台站均位于龙门山中央断裂西侧来看，似乎该模型略优．若真如此，则汶川主震的震源深度仅为8 km左右，这与张新东等(2013)的结果较为一致．

表  6  基于不同模型利用本文方法与Geiger法给出的汶川M_S8.0主震的定位结果

Table  6.  Relocation results of Wenchuan M_S8.0 earthquake based on different velocity models using the improved linear method in this paper for single event seismic location

下载: 导出CSV 

| 显示表格

表  7  基于不同模型定位结果的走时残差与其方均根误差比较

Table  7.  avel time residuals and their root-mean-square errors derived from different location results based on several velocity models

下载: 导出CSV 

| 显示表格

4.   讨论与结论

本文对线性单事件定位方法做了适当改进，使其在仅有P波到时资料和P波速度模型的情形下即可快速定位. 通过改进，使得定位计算不需要奇异值分解，而只需3-5次简单迭代即可给出地震发生的时空参数．理论检验表明，对单层均匀速度模型，本文改进方法可以给出较精确的定位结果．本文还结合改进方法在定位计算过程中能够根据不同震源深度相应地调整平均速度值这一特点，尝试将其推广应用于分层均匀模型的近源台网定位情形，讨论了其可行性、误差和适用范围，并对2008年汶川M_S8.0地震的时空参数进行了重新计算．

通过对方法的改进、理论测试和不同速度模型下的计算实验，以及与其它使用不同方法和不同台网资料给出的汶川M_S8.0定位结果比较，得到以下认识.

对地震定位这一经典地震学问题而言，初始破裂点对应的震中位置(经度和纬度)，只要有均匀的台网分布，即使采用不同的方法，甚至所用的速度模型有较大差异，通常都能给出较为一致且精度较高的结果(一般误差不超过1 km)．然而震源深度和发震时刻这两个参数，除与用于定位的台网资料和方法有关外，还与所用速度模型密切相关，而且二者难于解耦，往往出现此消彼长的现象．尤其是震源深度，由于可用于定位的实际台站对的海拔高程差太小，导致求解过程中系数矩阵出现高奇异值，因而目前仍然是地震定位参数中最不准确却又非常重要的参数．若要获得较高精度的震源深度值和发震时刻值，除另谋它法外，近震源小孔径台网的利用会有效地缩小系数矩阵的奇异值，也即近源小孔径台网的结果往往比远源大孔径台网的结果更精确．此外，如果能获取震中距小于或等于震源深度的近源台站资料(如本文的八角台，见图3)，其P波到时和S波与P波到时差对发震时刻和震源深度的求解精度能够形成有效的约束．换言之，如果有上述好的台站资料，即使采用最简单的方法也能给出较高精度的结果； 相反，如果没有近距离台站资料，即使采用再有效的计算方法，也很难取得令人满意的结果．

对汶川地震的时空参数，不同研究机构或个人给出的震中位置结果差异不大，但震源深度和发震时刻的差异均十分明显，这对于汶川地震的震源过程、断层构造、块体运动及地震成因等的正确认识非常不利，因而应当进一步展开深入研究和讨论．通过与前人研究结果的比较，本文进一步确认了汶川主震的发震时刻应为14时27分58秒左右； 震中位置与前人结果一致； 但震源深度明显偏小，仅为8—11.5 km(取决于所用速度模型)．为了验证本文结果的可靠性，计算了不同速度模型下各台走时残差和方均根误差，各种模型下的最大走时残差均小于0.14 s(表7)，其中两个模型小于0.10 s. 这样的走时误差范围从本文理论实验来看其对定位精度的影响是可接受的．我们还使用距离震中最近(震中距在5 km以内)的紫坪库水库台网八角台(BAJ)的S波与P波到时差(仅1.25 s，见图3)及其三分量初动波形资料，分别用“台站正下方地震”方法(Liu et al，2008)和视出射角为72°的倒推法(震中距参考汶川地震科学考察队参数)独立计算了单台震源深度，分别为8.33 km和9.85 km，与本文结果和张新东等(2013)结果非常接近．而后两种方法与本文方法是完全独立的．

本文改进的线性单事件定位方法，由于其原理、计算和对资料的要求相对简单，对近源台网定位和大震快速预警仍然是一种很适用的选择．但也要看到，由于地下速度结构的径向和横向不均匀性的客观存在，线性单事件定位方法必然有其局限性和适用范围．特别是当最大震中距超过60 km时，应用该方法所得震中位置误差不大，而发震时刻和震源深度值则因二者与折合速度的关系密切且无法相互解耦而存在一定的误差，此时该方法所得结果只能用作初步估计或其它方法的初值(牟磊育等，2006； 刘金丽，高见，2012)．

审稿专家对本文提出了宝贵意见和建议，作者在此表示衷心的感谢.