Mining for seismomagnetic information of geomagnetic Z component based on Copula theory
-
摘要: 利用Copula理论,选取天津地区5个台站的地磁资料,分析计算了1986—2013年的地磁Z值数据,经过在多种模型中比较Kendall与Spearman系数,得出最优模型,并分析不同周期下Kendall系数的时序曲线. 计算结果表明,在MS≥5.0地震前,Kendall系数的时序曲线处于紊乱期,震后其对应性迅速转好,一致性明显. 这是由于地震应力积累导致地下电性结构发生变化,而震后应力得到释放,磁场回归常态造成的. 尤为明显的是2006年文安MS5.1地震前,青光台(距震中最近)Kendall系数异于其它台站出现大幅下滑; 而2012年唐山MS4.8地震前,宁河台(距震中最近)Kendall系数异于其它台站上升幅度不大.
-
关键词:
- Copula函数 /
- Kendall系数 /
- Spearman系数 /
- 模型检验 /
- 地下电性结构
Abstract: In this paper, we selected geomagnetic data of five seismographic stations in Tianjin, analyzed and calculated geomagnetic Z component data from 1986 to 2013 based on Copula theory. After comparison of Kendall and Spearman coefficients in a variety of models, the optimal model was got, and then Kendall coefficient timing curves were analyzed in different cycles. The calculated results show that Kendall coefficient timing curve is in the disordered phase before the MS≥5.0 earthquake, and its consistency turns better rapidly after the earthquake. That is because the accumulated seismic stress causes the underground electrical structure to change, and the stress is released after the earthquake, magnetic field data returns to normal. It is more predominant that Kendall coefficient of the Qingguang seismographic station (it has the smallest distance from the epicenter) dropped sharply before the Wen’an MS5.1 earthquake in 2006, which is different from that of other stations; while Kendall coefficient of the Ninghe seismographic station (it has the smallest distance from the epicenter) rose marginally before the Tangshan MS4.8 earthquake in 2012. -
引言
在孕震过程中,随着地下介质应力的不断积累,其电导率会发生改变(龚绍京,吴占峰,1986; 冯志生等,2004,2009),导致感生的二次感应磁场的Z和H日变幅有异常变化(龚绍京等,1997). 不同结构上的大地电磁响应函数,如张量阻抗电阻率和地磁场测值的变化都可归结为感应电场或感生磁场的差异(马钦忠,钱家栋,2003). 临震前出现的地震构造过程,甚至会引起电流体系的剧烈变化,继而引起地磁内场或外场强度的变动(丁鉴海等,2008).由于震前震区周边的这种地下电性结构的变化,导致该区域数据形态及趋势可能会出现大体一致,但其变幅与离散度等均会出现被压制或被放大的细小变化.Copula函数通过计算选取适合的数值模型提取震磁信息,对数据集上尾与下尾的同步性给出秩相关,并结合震例,分析地震前后数据的时序曲线,由此在一定程度上对孕震期地下电性结构的变化与周边地震的关系予以反映.
本文基于Copula统计方法挖掘地磁异常信息,用以描述地震孕育地区及其附近地下岩石磁性的改变与地震发生的关系(丁鉴海等,2004; 马钦忠,2013).采用天津地区5个地磁台站21时的Z值分量,从1986年1月1日—2013年7月31日(27年7个月)的数据引入Copula函数进行分析,计算秩相关系数选取最适合的Copula函数模型,并在此模型下计算平方欧氏距离,得出27年来长期趋势约束下的模型和参数; 结合1995年唐山MS5.0地震,1998年张北MS6.2地震,2006年文安MS5.1地震,以及2012年唐山MS4.8地震等震例,绘出t-Copula模型下Kendall系数的时序曲线,进行震例分析,以找出在相似的原始数据变化形态下可能被埋没的地震前兆信号.
1. 研究方法
Copula函数广泛应用于金融、 水文、 气象信息预测等领域,是比较成熟的分析预报方法(韦艳华,张世英,2008; 宋松柏等,2012).其在相关性分析(任仙玲,张世英,2008; 林国龙等,2013)、 时间序列模型(张尧庭,2002; 杜本峰,郭兴义,2003; 韦艳华等,2003)、 时变相关模型(Frees,Valdez,1998)和变结构模型中有着广泛的应用.近年来,在水文气象中,该方法也得到相当深入的研究. 尤其在干旱分析、 洪水构建模型(张娜等,2008; 张雨,宋松柏,2010)等自然灾害方面,其在单变量概率分布、 多变量间的相依性度量、 参数估计、 随机数模拟以及最佳Copula函数的选择等方面都有着成熟的理论方法和应用.本文试图将该函数应用于地磁方面,希望能对地震地磁的研究工作铺设一条新的思路.
Copula函数作为一种连接函数,表征N个边缘分布函数与一个N维联合分布函数的关系,即满足随机向量x1,x2,…,xn的联合分布函数F(x1,x2,…,xn)与各自的边缘分布函数Fx1(x1),Fx2(x2),…,Fxn(xn)的连接关系(Nelsen,2006),即
F(x1,x2,…,xn)=C[ Fx1(x1),Fx2(x2),…,Fxn(xn)].
基于该函数预报方法的大体思路分为两步: 一是通过数学方法确定最优模型; 二是在此模型下计算各台站数据之间相关性系数的时序曲线,并结合震例进行预判.众所周知,震前由于应力积累,导致地下电性结构发生改变,引发的感应磁场导致附近台站的磁场测值发生异动. 应力慢慢地积累导致该异动也出现缓慢的微小变化,从而与其它台站间数据的相关性出现不一致,表现为长周期下震区附近磁值的相关性异于其它地区,其表征系数的时序曲线异于其它台站.
本文采用天津静海、 徐庄子、 青光、 宁河和塘沽等5个台站的数据作为样本,首先分析数据的基本形态,发现1980—1999年5个台站的数据呈上升趋势,1999—2006年处于平稳状态,2006年后又回归至上升趋势,故而对样本量进行这3个时段的划分,以达到在趋势一致情况下的参照比对效果; 然后剔除由于台站基建和仪器维修等造成的缺数,并剔除因为环境及人为干扰等造成的台阶和突跳等数据,从而得到5个台站中符合计算的数据信息时段,且提高该信息时段内的数据可靠度; 之后再计算数据的峰度、 偏度等形态指标,以非参数法绘制经验分布函数图和核分布函数估计图,使数据在保证趋势的情况下得到有效的对比,并绘制频数与频率直方图; 继而进行参数估计得出Kendall秩相关系数和Spearman秩相关系数,判定所得数据与这些模型函数之间的相关性,并以静海台为参照标准,对其它4个台数据与静海台差值做Copula函数的计算选取,即通过二元正态Copula函数(谢中华,2010)

或二元t-Copula函数

和Archimedean Copula函数(Genest,Mackay,1986)等确定最优模型; 最后通过几何平方欧氏距离对模型进行评价(欧氏距离越小,效果越好).在震例选取和分析中,选取1986—2003年8月以参照台(静海台)为圆心的350 km以内的MS≥6.0地震(1998年1月10 日张北MS6.2地震),300 km以内的MS≥5.0地震(1995年10月6 日唐山MS5.0地震和2006年7月4 日文安MS5.1地震),以及150 km以内的MS≥4.5地震(2012年5月28日唐山MS4.8地震),联合Kendall系数的时序曲线进行相关分析.
2. 数值计算与模型选取
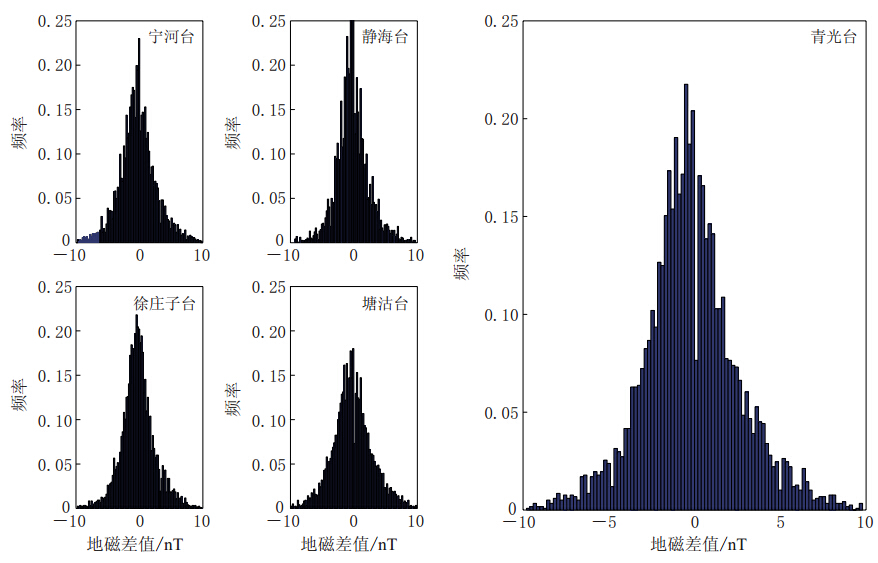
由于夜间干扰小,选取比较平稳的21时Z值的逐日差分数值,在剔除干扰数据之后,为确定随机变量x(宁河台)、 y(静海台)、 a(徐庄子台)、 b(塘沽台)、 c(青光台)的分布类型,采用Matlab编制程序,用ecdf和ecdfhist绘制频率图,并调用skewness函数和kurtosis函数分析数据形态,结果见图1和表1.
表 1 5个台站的偏度与峰度Table 1. Skewness and kurtosis of five stations
从表1可以看出,宁河台的偏度较大且峰度也较大,静海台的偏度最小,塘沽台的峰度最小.需要说明的是,图1中5幅图x轴取0.1时的数据均出现了不同程度的低值,这是由于在读取数据时采用了“奇进偶不进”的计算原则造成的,即当数据为0.5需要进位时,人为地查看个位数据的奇偶性,如为奇数即进位,若为偶数则不进位.这一原则与计算机默认的“逢5进位”不同.由于各数据均在统一规则下,不会对最终的模型选取结果产生影响,故不对此作样本概率的修改.
调用jbtest,kstest和lillietest函数对5个台站进行正态性检验,结果如表2所示.
表 2 5个台站的正态性检验Table 2. Normality test of five stations
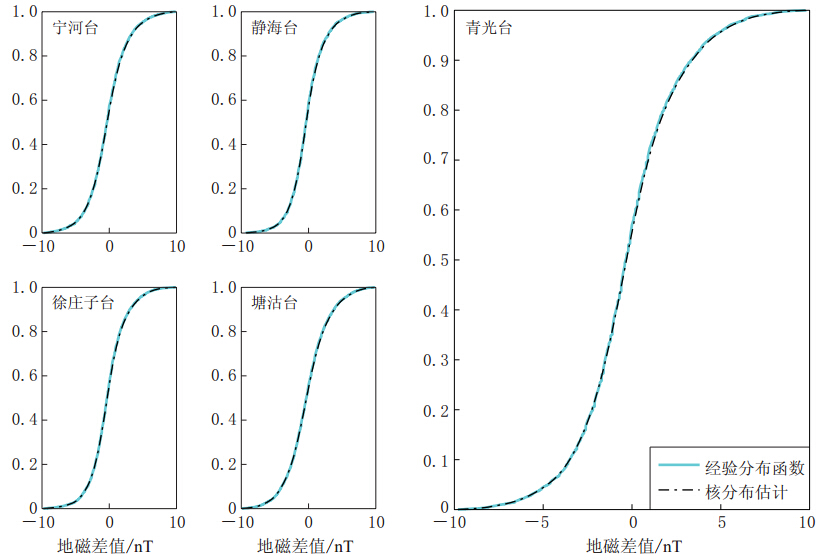
从表2可以看出,5个台站均不属于正态分布.使用非参数法,调用ecdf函数求样本经验分布函数,作为总体分布函数的近似;调用ksdensity函数,用核光滑法进行总体分布的估计;对二者作同图比对.结果如图2所示.
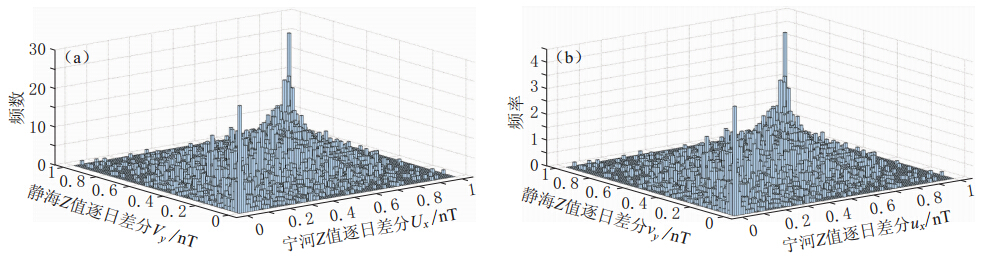
由图2可以看出,各台站的经验分布函数与核分布估计曲线重合性很好.横坐标即函数返回的向量代表各自经过排序后的样本数据,实线表示分别与该向量对应的经验分布函数值向量,虚线表示核分布估计值. 实际上两条曲线的数值是有差别的,只是差别非常微小,使二者几乎重合. 由于确定了x,y,a,b,c(5个台站)的边缘分布,根据计算得出的分布估计数值,绘制频数图(Ux,Uy,Ua,Ub,Uc; Vx,Vy,Va,Vb,Vc)并以此为参考标准绘制频率图(ux,uy,ua,ub,uc; vx,vy,va,vb,vc),它可以作为频数图(Ux,Uy,Ua,Ub,Uc; Vx,Vy,Va,Vb,Vc)的联合密度函数的估计(任仙玲,张世英,2007). 其结果见图3.
由图3可看出,宁河台的数据集均显示出较高的上尾和下尾,其余3个台对静海台的 上下尾高值图像与宁河台类似. 为进一步确定模型,调用copulafit函数计算二元正态Copula的参数、 二元t-Copula 的线性相关参数,以及自由度和置信空间等值.计算结果见表3.
表 3 不同模型的相关参数表Table 3. The relevant parameter table based on different models
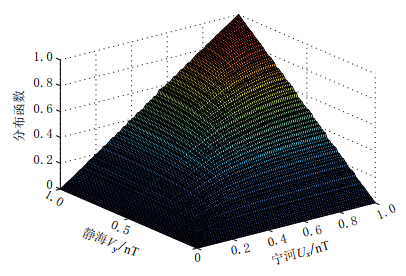
根据表3中的参数,调用copulapdf和copulacdf函数计算并分别绘制Copula和t-Copula函数的密度函数(图4a,c)与分布函数(图4b,d)(Bouye et al,2000; Cherubini et al,2004).
从图4中,以宁河台为例,可以看出二元t-Copula函数比二元正态Copula函数具有更厚的尾部,更能较好地反映变量间的尾部相关性. 4个台站的二元t-Copula模型表达式分别可以近似为

调用copulastat函数求Kendall和Spearman秩相关系数,结果见表4.
表 4 Kendall与Spearman系数表Table 4. Kendall and Spearman coefficients
由表4可见,二元t-Copula函数的Kendall系数更接近于CORR(原始观测数据所求的)Kendall数值. 由Kendall系数的定义(Hollander,Wolfe,1973; Lehmann,1975)

可知,在N个样本中取r个样本的组合数,其样本数量一致与否的差对该组合数的商,表征了样本的一种相关性.
而二元正态Copula函数的Spearman系数则更接近于CORR(原始观测数据所求的)Spearman数值. 由Spearman系数的定义(Lehmann,1966)

可知,它表征了数据一致与否的概率之差,是样本相关性的另一种表述.
综上所述,该例中Kendall系数更适用于二元t-Copula函数模型,而Spearman系数则更适用于二元正态Copula函数模型.
3. 模型评价
由二元t-Copula与二元正态Copula分别对经验Copula分布函数做欧氏平方距(图5). 由表5可以看出,二元 t-Copula的欧氏平方距远小于二元正态Copula模型,所以选择二元t-Copula函数模型更为适合.且宁河台、 徐庄子台对静海台的数据拟合得最好.
表 5 二元正态Copula和二元t-Copula模型评价Table 5. Evaluation of bivariate normal Copula and bivariate t-Copula models
4. 联合震例分析
分别选取1986年1月—2003年8月以静海台为圆心的350 km以内的MS≥6.0地震(1998年1月10日张北MS6.2地震),300 km以内的MS≥5.0地震(1995年10月6日唐山MS 5.0地震、 2006年7月4日文安MS 5.1地震),以及150 km以内的MS≥4.5地震(2012年5月28日唐山MS4.8地震),对1986年以来的数据进行Kendall秩相关周期分析,选取周期为90,180,270,365,540天和720天的Kendall系数,联合以上地震绘出时序曲线(图6).
孕震区在孕震过程中,由于地下应力的不断积累,使地下介质产生空隙,地下水有可能顺着裂隙充注至空隙中,导致地下介质的电导率发生改变,从而改变地下电性结构,引起二次感生磁场,最终导致电磁环境发生缓慢而微小的变化. 通过对比这种变化的相关性,找出地下应力与磁变、 地下电性结构与地震之间的关系.该相关性由Copula函数提取震磁信息建模计算中得到.
图6中震前存在相关性差(应力积累—地下电性结构变化—相关性不一致)及震后相关性转好(应力彻底释放—地下电性结构恢复—相关性恢复一致)的特点,且该特点长周期表现明显(周期为540天、 720天).
从图6中可以看出以下特点:
1)1995年10月6日唐山MS5.0地震前,在周期T=720天图像上,徐庄子台异于其它3个台快速上升,表现为相关性不一致; 而震后4条曲线趋势短暂地趋于一致,但之后徐庄子台再次加速上升,4条曲线一致性又出现混乱,随后在张北MS6.2地震后恢复一致.
2)1998年1月10日张北MS6.2地震前,在周期为720天图像上,徐庄子台相关性迅速上升,青光台缓慢上升,塘沽台和宁河台缓慢下降,4个台相关性不一致; 而地震后约500天,Kendall系数趋于一致且同步性好,均为缓慢上升.同年4月14日(相距不到100天)唐山发生MS4.7地震,符合本文的择震标准.本文认为这次地震与张北地震有一定联系,对张北地震的解释完全可以用来解释它,即应力积累到一定程度,张北地区首先断裂,进行应力释放. 唐山老震区地下结构复杂、 脆弱,距张北仅200余千米,紧随其后进行了应力调整. 这是可以理解的.
3)2006年7月4日文安 MS5.1地震前,青光台相关性表现为迅速下降,而宁河台为快速上升,徐庄子台和塘沽台平稳有降,4个台相关性差; 而地震后约1 000天,Kendall系数趋于一致且同步性好. 该震后相关性没有迅速恢复一致的原因可能是应力没有彻底释放,在震后应力经过缓慢释放后,曲线趋于一致,甚至重合.
4)2012年5月28日唐山MS4.8地震,由于该地震震级较小,积累的应力小,震前宁河台(距震中最近)Kendall系数异于其它3个台,上升幅度不大. 在徐庄子台、 青光台、 塘沽台的相关性迅速向上“爬”的时候,宁河台实际上只向上“爬”了一点点(在周期为540天的图上明显).实际上在270天、 365天的周期图上,宁河台已经明显存在异于其它3个台的变化形态.在震后540天、 720天周期图上,宁河台趋势由升转降,显示与其它3个台的趋势(一致向上)不同. 这是由于此次唐山MS4.8地震并未能彻底释放地下应力所致. 如果未来唐山老震区不断有小震释放能量,4条曲线趋势将慢慢趋于一致; 如果未来唐山老震区小震少,宁河台仍持续异于其它3个台,则应密切关注该区的地震危险性.
综合上述联合震例分析推断,地震与Kendall系数时序曲线趋势的改变可能有一定的关系.
5. 讨论与结论
一般说来,震中距越小,地下应力变化越显著. 考虑到地下岩石构造不同,受力方向与承压阈值不同等地质因素,也会存在个别区域震中距小而烈度小的情况. 但由于本研究区域很小,均处于华北平原带北部,地质背景基本相同,相邻台站间不超过50 km,各台年变、 季节变基本一致,磁暴等非地震因素也非常同步; 又因选用的是差值数据进行分析,日变幅度超10 nT的突变和台阶全部滤掉,其外部变化的影响可以弱化到不计.本文研究所用时间较长(27年多),时间跨度约10 000天,即使有大磁暴影响数十天,在此范围内对大趋势的影响也不到1%.本文分周期计算是为了反映不同周期下的相关性趋势. 长周期尺度的时序曲线因其计算样本量大,模型信度高,能很好地表述变化,且由于环境干扰小,更应受到关注(陈伯舫,2000).
本文正是通过这种小范围、 大时间尺度的分析,最大限度地避免了各种外界可能的影响,首次将成熟的Copula模型理论应用于地磁数据中,希望能用这种方法挖掘出有用的震磁信息.本文主要结论如下:
1)经计算评价,二元t-Copula模型的欧氏平方距远小于二元正态Copula模型,认为二元t-Copula函数模型是最优模型.
2)地震之前,Kendall系数的时序曲线处于紊乱期,震后其对应性迅速转好,一致性明显.即各台数据表现为震前相关性差,震后相关性变好.这种现象符合“孕震期地下应力拉张导致岩石磁性变化,慢慢积累的这种变化,使台站间的相关性变差”的理论.而地震后应力释放,地下电性结构恢复稳定,各台之间的相关性又趋于同步.
此外,在假定应力变化与震中距成正比的前提下,在小范围内,距震中最近台站的相关性在震前出现异于其它3个台站的现象,且近震表现出的可能性大.即距震中最近的台站在震前有不一致的表现.例如在图6中: 2006年7月4日文安 MS5.1地震前,青光台(距此次地震最近)数据异于其它3个台数据,出现大幅下滑至最低点(周期为540天、 720天); 2012年5月28日唐山 MS4.8地震前,Kendall系数处于急速上升期(周期为270,365,540,720天),而宁河台(距此次地震最近)的上升却处于被压制状态,幅度明显小于其余3个台数据,且在长周期表现明显(周期为540,720天).但在其它两个震例中却无此现象. 这种情况还需进一步总结分析其它地区震例,以待解释说明.
作为一种新的挖掘震磁信息方法的探索,虽然选取的区域台站比较密集(天津5个台),数据时间较长(1987—2013年),但是华北已经16年多未发生MS≥6.0地震,MS≥5.0的地震也是屈指可数. 考虑到仪器监测范围能力有限,如果扩大震例范围,分析起来不免过于牵强,所以震例缺乏是本文分析中的一个无奈之处. 但是即便是几个震例,仍然能清晰地看出上述结果,因此对使用Copula方法挖掘震磁信息还是有一定意义的.今后在使用本方法进行深入研究时,建议选取更好的区域条件进行,进一步推广该方法在地学中的应用价值.
-
表 1 5个台站的偏度与峰度
Table 1 Skewness and kurtosis of five stations

表 2 5个台站的正态性检验
Table 2 Normality test of five stations

表 3 不同模型的相关参数表
Table 3 The relevant parameter table based on different models

表 4 Kendall与Spearman系数表
Table 4 Kendall and Spearman coefficients

表 5 二元正态Copula和二元t-Copula模型评价
Table 5 Evaluation of bivariate normal Copula and bivariate t-Copula models

-
陈伯舫. 2000. 单台地磁夜均值资料研究半年周期变化的电磁响应[J]. 地震学报, 22(3): 297-304. Chen P F. 2000. Electromagnetic response function for the semi-annual variations estimated by the single station method using the night-time values of the geomagnetic fields[J]. Acta Seismologica Sinica, 22(3): 297-304 (in Chinese).
丁鉴海, 刘杰, 余素荣, 肖武军. 2004. 地磁日变化异常与强震的关系[J]. 地震学报, 26(增刊): 79-87. Ding J H, Liu J, Yu S R, Xiao W J. 2004. Geomagnetic diurnal-variation anomalies and their relation to strong earthquakes[J]. Acta Seismologica Sinica, 26(Suppl.): 79-87 (in Chinese).
丁鉴海, 卢振业, 余素荣. 2008. 地震地磁学概论[M]. 合肥: 中国科学技术大学出版社: 159-162. Ding J H, Lu Z Y, Yu S R. 2008. A Brief Treatise on Seismomagnetism[M]. Hefei: University of Science and Technology of China Press: 159-162 (in Chinese).
杜本峰, 郭兴义. 2003. 一种新的风险度量工具: PaV及其计算框架[J]. 统计研究, 20(2): 48-50. Du B F, Guo X Y. 2003. A new risk measurement risks: PaV and computational framework[J]. Statistical Research, 20(2): 48-50 (in Chinese).
冯志生, 梅卫萍, 张秀霞, 庄明龙, 张晓勇. 2004. 中强震前地磁谐波振幅比的趋势性变化特征初步研究 [J]. 西北地震学报, 26(1): 50-56. Feng Z S, Mei W P, Zhang X X, Zhuang M L, Zhang X Y. 2004. Preliminary study on the characteristics of long and medium term variation for the amplitude ratio of geomagnetic humorous wave before moderate-strong earthquakes[J]. Northwestern Seismological Journal, 26(1): 50-56 (in Chinese).
冯志生, 居海华, 李鸿宇, 杨从杰, 立金柱. 2009. 地磁谐波振幅比异常特征的进一步研究及定性解释[J]. 华南地震, 29(1): 17-23. Feng Z S, Ju H H, Li H Y, Yang C J, Li J Z. 2009. Further study on characteristics of long-term and mediun-term variations of geomagnetic harmonic wave amplitude ratios before moderate or strong earthquakes[J]. South China Journal of Seismology, 29(1): 17-23 (in Chinese).
龚绍京, 吴占峰. 1986. 唐山地震可能伴随的地电导率变化[J]. 地震学报, 8(1): 28-35. Gong S J, Wu Z F. 1986. Possible changes of earth conductivity accompanying the Tangshan earthquake of 1976[J]. Acta Seismologica Sinica, 8(1): 28-35 (in Chinese).
龚绍京, 陈化然, 张翠芬, 马淑芹, 杨桂君. 1997. 地磁水平场转换函数在唐山地震前的异常反应[J]. 地震学报, 19(1): 51-58. Gong S J, Chen H R, Zhang C F, Ma S Q, Yang G J. 1997. Abnormal reaction of geomagnetic horizontal field transfer function before Tangshan earthquake[J]. Acta Seismologica Sinica, 19(1): 51-58 (in Chinese).
林国龙, 叶善椿, 韩军, 胡佳佳. 2013. 基于Copula理论的FFA市场相关性研究[J]. 上海海事大学学报, 34(1): 62-67. Lin G L, Ye S C, Han J, Hu J J. 2013. Research on dependency in FFA market based on Copula theory[J]. Journal of Shanghai Maritime University, 34(1): 62-67 (in Chinese).
马钦忠, 钱家栋. 2003. 地下电性非均匀结构对地电场信号的影响[J]. 地震, 23(1): 1-7. Ma Q Z, Qian J D. 2003. The influence of inhomogeneous geoelectric structure on the signals of geoelectric field[J]. Earthquake, 23(1): 1-7 (in Chinese).
马钦忠. 2013. 《与地震有关的电磁现象及其机理和观测研究专辑》前言[J]. 地震学报, 35(1): 1-3. Ma Q Z. 2013. Preface to the special issue: Study on earthquake-related phenomena, their mechanism and observation[J]. Acta Seismologica Sinica, 35(1): 1-3 (in Chinese).
任仙玲, 张世英. 2007. 基于核估计及多元阿基米德Copula的投资组合风险分析[J]. 管理科学, 20(5): 92-97. Ren X L, Zhang S Y. 2007. Risk analysis of portfolio investment based on kernel estimation and multivariate Archimedean Copula[J]. Journal of Management Sciences, 20(5): 92-97 (in Chinese).
任仙玲, 张世英. 2008. 基于Copula函数的金融市场尾部相关性分析[J]. 统计与信息论坛, 23(6): 66-71. Ren X L, Zhang S Y. 2008. Tail dependence analysis of financial market based on the Copula[J]. Statistics & Information Forum, 23(6): 66-71 (in Chinese).
宋松柏, 蔡焕杰, 金菊良, 康艳. 2012. Copulas函数及其在水文中的应用 [M]. 北京: 科学出版社: 312-315, 328-360. Song S B, Cai H J, Jin J L, Kang Y. 2012. Copulas Function and Its Application in Hydrology[M]. Beijing: Science Press: 312-315, 328-360 (in Chinese).
韦艳华, 张世英, 孟利锋. 2003. Copula理论在金融上的应用[J]. 西北农林科技大学学报: 社会科学版, 3(5): 97-101. Wei Y H, Zhang S Y, Meng L F. 2003. Copula theory and its application in finance[J]. Journal of Northwest Sci-Tech University of Agriculture and Forestry: Social Science Edition, 3(5): 97-101 (in Chinese).
韦艳华, 张世英. 2008. Copula理论及其在金融分析上的应用[M]. 北京: 清华大学出版社: 32-35. Wei Y H, Zhang S Y. 2008. Copula Theory and Its Applications in Financial Analysis[M]. Beijing: Tsinghua University Press: 32-35 (in Chinese).
谢中华. 2010. MATLAB 统计分析与应用: 40个案例分析[M]. 北京: 北京航空航天大学出版社: 187-213. Xie Z H. 2010. MATLAB Statistical Analysis and Applications: 40 Case Studies[M]. Beijing: Beihang University Press: 187-213 (in Chinese).
张娜, 郭生练, 闫宝伟, 刘攀. 2008. Copula函数在分期设计洪水中的应用研究[J]. 水文, 28(5): 28-32. Zhang N, Guo S L, Yan B W, Liu P. 2008. Seasonal design flood based on Copula function[J]. Journal of China Hydrology, 28(5): 28-32 (in Chinese).
张雨, 宋松柏. 2010. Copulas函数在多变量干旱联合分布中的应用[J]. 灌溉排水学报, 29(3): 64-68. Zhang Y, Song S B. 2010. Application of archimedean Copulas in multi-variable drought distribution[J]. Journal of Irrigation and Drainage, 29(3): 64-68 (in Chinese).
张尧庭. 2002. 连接函数(Copula)技术与金融风险分析[J]. 统计研究, 19(4): 48-51. Zhang Y T. 2002. Copula technique and financial risk analysis[J]. Statistical Research, 19(4): 48-51 (in Chinese).
Bouye E, Durrleman V, Nikeghbail A, Riboulet G, Roncalli T. 2000. Copulas for Finance: A Reading Guide and Some Applications[Z]. London: Financial Econometrics Research Centre, City University Business School: 2-6.
Cherubini U, Luciano E, Vecchiato W. 2004. Copula Methods in Finance[M]. New York: John Wiley & Sons Ltd: 16-23.
Frees E W, Valdez E A. 1998. Understanding relationships using Copulas[J]. North American Actuarial Journal, 2(1): 1-25.
Genest C, Mackay J. 1986. The joy of Copulas: Bivariate distributions with uniform marginals[J]. American Statistician, 40(1): 280-283.
Hollander M, Wolfe D A. 1973. Nonparametric Statistical Methods[M]. New York: John Wiley & Sons Ltd: 151-158.
Lehmann E L. 1966. Some concepts of dependence[J]. Ann Math Statist, 37(5): 1137-1153.
Lehmann E L. 1975. Nonparametrics: Statistical Methods Based on Ranks[M]. San Francisco: HoldemDay Inc: 46-57.
Nelsen R B. 2006. An Introduction to Copulas[M]. New York: Springer: 1-5.
-
期刊类型引用(4)
1. 张明东,刘建波,张玮,吴博洋,廖晓峰. 天津塘沽台直流视电阻率下降异常的成因分析. 地震学报. 2023(04): 671-684 .  本站查看
本站查看
2. 张明东,何康,廖晓峰,丁晶,曹颖. 基于伪魏格纳-维勒分布的地磁场时频分析研究——以中国大陆东部地区为例. 地震. 2018(01): 61-73 .  百度学术
百度学术
3. 张明东,曹颖,吴博洋,刘长生,张长轩. 基于Savitzky-Golay算法的地磁去扰研究. 微波学报. 2018(S2): 474-476 .  百度学术
百度学术
4. 刘长生,赵谊,张明东,李继业,马艳丽,战玉明,刘彦彬. 吉林松原M≥5.0震群前地磁谐波振幅比异常特征. 地震地磁观测与研究. 2017(02): 81-88 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: