Applications of FFT and DFT in amplitude-frequency characteristic test of seismic data recorders
-
摘要: 在进行地震数据采集器的幅频特性测试中,当标定信号频率稍高时(约为采集器采样率1/5以上),采集器输出的正弦波形发生畸变,无法人工读取正弦波峰值.为了解决该问题,本文提出了基于离散傅里叶变换(DFT)的积分恢复算法,将该方法与快速傅里叶变化(FFT)谱分析方法同时应用于一台高精度地震数据采集器的幅频特性测试数据处理.结果表明这两种算法均能标准化、高精度地完成采集器幅频特性标定数据的计算.其中基于DFT的积分恢复算法的计算程序操作简单,能够高效率地完成数据采集器的幅频特性检定工作;并且该方法还可以应用于地震数据采集器的线性度测试.Abstract: During the process of amplitude-frequency characteristic test of seismic data recorders, when the frequency of calibration signal reached one-fifth of the sampling frequency of seismic data recorder, we cannot manually get the peak-value of output sine-wave by seismic data recorder due to distortion of sine-waveforms. In order to solve this problem, this paper proposed aDFT(discrete Fourier transformation)-based numerical integration method. Then FFT (fast Fourier transformation) method and DFT numerical integration method were used to compute real amplitude-frequency characteristic test data of one high-precision seismic data recorder. The result shows that these two methods are high precision and standardization, and can compute the calibrating data of amplitude-frequency characteristic. Compared with FFT method, DFT-based numerical integration method is simple to operation. And it can also be applied to linearity test of seismic data recorders.
-
引言
为了更好地完成全国范围内的地震动监测任务,目前我国建立了国家数字地震台网、区域数字地震台网、流动数字地震台网等多种地震动监测网络.这些地震动监测网络中运行着大量的地震数据采集器、地震计等设备,这些设备是由多个不同生产厂家、多批次供应的多种不同类型设备,因此不同类型设备性能不同,技术参数差别较大,加大了地震设备维护人员的工作量.为了提高地震动监测系统的效能,保障地震动台网健康运行,迫切地需要对在网运行的地震仪器进行标准化质量检测工作.
地震数据采集器是实现数据转换及数据记录的重要仪器,其待检测技术指标包含噪声、最大允许输出误差、互调失真度、线性度、共模抑制比、路际串扰比、幅频特性、输入电阻等10多项指标,另外还有事件检测、数据记录等多项功能均需要进行测试验证是否能有效工作.中国地震局发布的《地震数据采集器质量检测技术规程(试行)》中国地震局监测预报司.2010.地震数据采集器质量检测技术规程(试行).13-15.中给出了这些技术指标的纲要性测试方法.但这些测试方法还不够细致和全面,其中部分技术指标测试时的仪器连接方式、环境要求或数据计算方法等因素尚未具体化.而这些因素会对地震数据采集器质量检测结果产生一定影响.为了完善地震数据采集器质量检测方法,本文在《地震数据采集器质量检测技术规程(试行)》的基础上进行地震数据采集器幅频特性的测试研究工作,给出应用于幅频特性测试的标准化的最大峰值计算方法.
1. 地震数据采集器质量检测
地震数据采集器和地震计是进行地震观测的关键设备.其中地震计负责检测出微弱地震动信号并转换为模拟电压值;地震数据采集器负责完成模拟地震观测信号到数字信号的转换、数据整理、数据存储、网络接入、数据传输服务等多种功能.地震数据采集器的产品质量直接决定地震数据的质量,其技术指标也直接影响地震观测数据的质量,其技术参数的表达方式也直接影响地震观测数据的使用.为了保证地震监测设备运行状态正常、技术指标正常、保障各级地震监测网络获取高质量的监测数据,需要对地震数据采集器进行全面系统的质量检测及仪器技术指标校验工作.因此,需要研究地震数据采集器的关键性技术参数的标准化检测方法及其对地震观测数据的影响.
本研究中使用了Q330HRS型高精度数据采集器记录数据.表1给出了这种类型地震数据采集器的基本技术指标.
表 1 Q330HRS型高精度数据采集器基本技术指标Table 1. Main specifications of Q330HRS high precismic data recorder
表1中介绍的数据采集器指标是仪器厂家给出的简单技术指标,并不能完全代表该地震数据采集器的性能.实际地震监测及工程应用中,我们更加关注的采集器指标包括噪声、幅频特性、线性度、动态范围、共模抑制比、 路际串扰比、授时误差、守时精度等多项内容,这些技术指标的优劣都将反映在地震监测数据的质量上.为了提高地震监测数据质量,实现地震监测标准化,地震监测系统的研究人员已经开始了一系列的地震监测仪器标准化测试工作,本文将结合数据采集器质量检测中的幅频特性标准化测试方法进行介绍.
2. 地震数据采集器幅频特性测试方法
常用的地震数据采集器幅频特性测试方法为:将标准信号源连接到数据采集器的输入端,调节信号源的输出信号幅度为采集器满量程的50%;保持信号源输出幅值不变,调节标准信号源输出信号频率,本着测试信号频率覆盖低频带端到高频截至频率点的原则,变换多个测试频率点,使数据采集器记录每个测试频点的测试数据,记录数据的时间至少要保持10s,并要保证至少记录到一个完整的信号周期.记录每一个测试频点f的地震数据采集器的输出信号,该输出信号为频率fi、单向最大峰值Ai的正弦波.其中正弦波的单向最大峰值需要从记录波形中以一定方法来读取,然后按照式(1)进行归一化的幅频特性计算.

式中,FR为归一化幅频特性,Ai为第i个测试频率点的数据采集器输出的正弦波单向最大峰值(单位为V),A5Hz对应输入频率为5Hz时数据采集器输出的正弦波单向最大峰值.
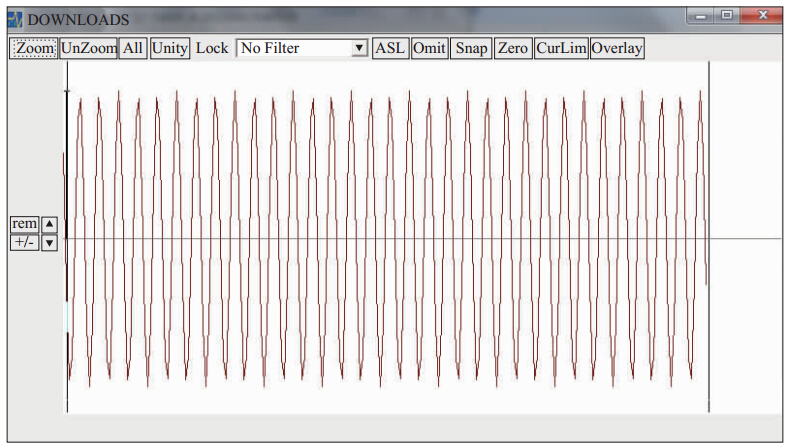
根据上述测试方法进行测试,取得每个测试频率点的单向峰值最大值,按式(1)进行计算即可得到数据采集器的这一采样率的幅频特性数据.原有的方法基本是人工读取每个测试频率点的单向峰值最大值,读取的数据误差大、方法不规范;并且在上述幅频特性测试过程中,发现采集器在100Hz采样率下、输入信号频率为20-45Hz时(其它采样率下也存在此问题),采集器采集到的信号显示不是一个标准正弦波,而是出现了正弦波的峰值高低起伏,表现为波形畸变(图1),这时已经无法人工读取采集器输出的峰值数据.这种高频标定频率下的波形畸变现象是数据采集器正常性能的表现,也符合采样定理.但此时不能继续简单地读取正弦波的峰值,亟需一种标准计算方法来完成采集器输出正弦波峰值计算.
3. 地震数据采集器幅频特性测试数据处理方法
根据采样定理,进行模拟/数字信号的转换过程中,当数据采集器的采样率大于信号中最高频率的2倍时,采样之后的数字信号则完整地保留了原始信号中的相关信息.即理论上通过相应的数据处理办法,可以从数据采集器显示畸变的数据中恢复出实际正弦波形的最大峰值及对应频率值.在数据采集器的幅频特性测试中每个正弦波频率是已知的,需要计算的只是数据采集器记录的正弦波信号最大幅值.本文采用FFT谱分析方法和基于DFT的数据积分恢复方法进行采集器幅频特性测试输出信号的单向最大峰值计算.
3.1 FFT谱分析方法
FFT谱分析方法是将以时间为自变量的离散序列与以频率为自变量的频谱序列之间建立变换关系(黄爱苹,1991;张德丰,2010).因此FFT谱分析计算结果曲线图的横坐标表示的是各个频率点信息,而纵坐标表示的是幅值信息.以MATLAB编程语言编写的计算程序关键语句只有一行,即yn=2*abs(fft(xn,N)/N). 其中,xn为地震数据采集器的数据文件向量,N为地震数据采集器的数据文件向量长度.
根据该计算结果,从中选出最大值即为该采集器输出正弦波信号的单向峰值最大值.该算法的MATLAB程序简单,但进行实际采集器幅频特性标定数据计算处理时,需要在程序代码中手动改变数据文件名称、 数据长度N,人工操作不方便且工作量大.
3.2 基于DFT的数据积分恢复方法
对地震数据采集器进行幅频特性标定时,当以正弦波输入数据采集器后,数据采集器的输出也是一个正弦波(周期函数).而从数学角度上看,一个周期函数可以分解为不同频率的正弦函数和的形式,即周期为T的函数f(t)可以表示为如下形式(张宗达等,1997):

对该周期函数f(t)进行傅里叶变换,则公式为

将欧拉公式e-imωt=cosmωt-isinmωt代入上式中,则

将式(4)展开,得

根据三角函数的正交性,当n≠m时,式(5)中的第1项和第4项为零,而第2项和第3项不为零,进一步计算结果为

利用三角函数积化和差公式可以得出

由于采集器输入信号只有一种频率的正弦波,式(7)中的n只能为一个自然数,不再是无穷个自然数.对式(7)两端复数进行模值计算,则

对地震数据采集器的每个标定频率点的幅频特性标定数据进行式(3)的积分计算,则所得结果与式(8)的结果相等,即

式中An即为特定标定信号频率下的地震数据采集器的单向最大峰值.
而实际上地震数据采集器输出信号为离散数据,即选用一段足够长的数据f(n),n=1,2,3,…,N,对该序列进行离散傅里叶变换(DFT),则

当进行DFT的数据足够长(即N足够大)时,该DFT结果无限接近于对应连续数据的傅里叶变换结果,即式(9)的模值结果近似等于式(10)的模值结果,则

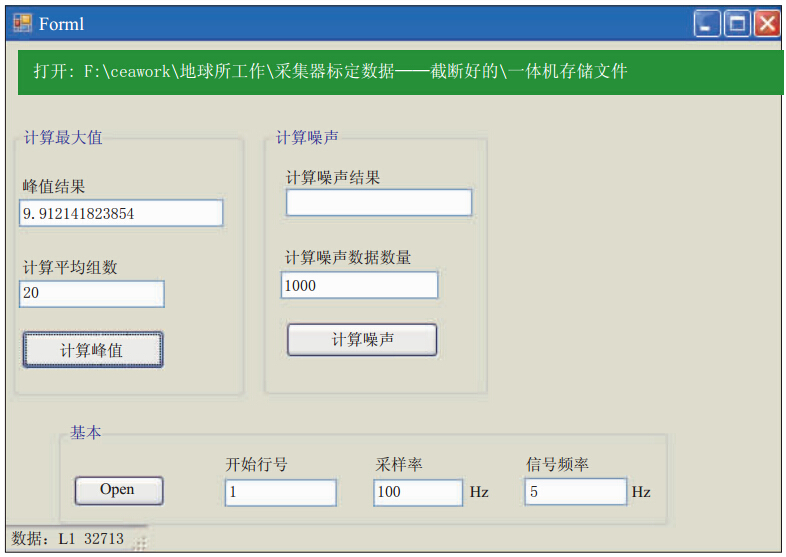
本文依据式(11),基于VisualC#软件平台编写了该采集器幅频特性的DFT算法的程序.该程序不仅可以高精度地完成计算,而且支持可视化界面操作,可以很方便地读入数据采集器采样率、标定信号频率、采集器输出的标定数据文件等必需的参数,并且在程序界面可直接输出该采样率下的最大幅值(图2).
4. 地震数据采集器幅频特性测试及误差分析
以Q330HRS型地震数据采集器为例,采用经过权威计量单位检定过的Agilent-33552A型信号发生器作为标定信号源对该数据采集器进行了幅频特性测试.在进行标定测试时,该信号源输出信号为标准正弦波,信号源输出正弦波幅值最大值为10 V,而输出信号频率变化.Q330HRS型采集器的工作参数为100 Hz,各通道放大倍数为1、无滤波器.对该采集器的6个测量通道进行0.001—45 Hz的幅频特性标定.表2给出了该数据采集器通道1的幅频特性标定数据,采用基于DFT谱分析的数据积分恢复算法程序的计算结果.表3给出了两种不同计算程序的幅频特性标定结果.该数据点数根据《地震数据采集器质量检测技术规程(试行)》 中国地震局监测预报司. 2010. 地震数据采集器质量检测技术规程(试行). 13-15.资料,记录时间不少于10 s,即N≥10 s· 100 Hz=1 000个.从表3中可以看出,两种方法的计算结果基本相同.而从本文对相同测试数据的处理过程也可以看出,采用DFT算法程序,操作简单、操作处理速度快;而采用FFT算法程序操作繁杂、操作处理速度慢.
表 2 Q330HRS采集器幅频特性标定数据(DFT算法)Table 2. Amplitude-frequency characteristic calibration data of Q330HRS seismic data recorder with DFT method 表 3 两种不同算法采集器幅频特性标定结果Table 3. Amplitude-frequency characteristic calibration data of Q330HRS seismic data recorder with two method
表 3 两种不同算法采集器幅频特性标定结果Table 3. Amplitude-frequency characteristic calibration data of Q330HRS seismic data recorder with two method
为了得出两种计算方法的计算误差,本文对不同标定信号频率fc下的采集器输出信号进行了如下计算处理:
1)对于标定信号频率满足0.001 Hz≤fc<0.01 Hz,选择不少于10个标定信号周期 长度数据进行采集器输出信号的单向最大峰值计算.其中计算数据长度为N≥10(1/fc)Fs,Fs为采集器的采样率.计算出的电压幅值为该标定信号频率下采集器输出正弦波峰值的约定真值Vtc.
2)对于标定信号频率满足0.01 Hz≤fc<1 Hz,选择不少于100个标定信号周期长度数据进行采集器输出信号的单向最大峰值计算.其中计算数据长度为N≥100(1/fc)Fs.计算出的电压幅值为该标定信号频率下采集器输出正弦波峰值的约定真值Vtc.
3)对于标定信号频率满足1 Hz≤fc<45 Hz,选择不少于1 000个标定信号周期长度数据进行采集器输出信号的单向最大峰值计算. 其中计算数据长度为N≥1 000(1/fc)Fs.计算出的电压幅值为该标定信号频率下采集器输出正弦波峰值的约定真值Vtc.
从理论上讲,当计算数据量非常大时,FFT算法、DFT算法计算结果即为真实值.因此分别采用FFT程序、DFT算法程序对采集器进行式(1)—式(3)的大数据量的幅频特性计算,得到采集器输出幅频特性的约定真值Vtc.将表3中各标定频率下的采集器输出正弦波峰值Vc与约定真值Vtc相减,得到各标定频率下的正弦波峰值的绝对误差ΔVc,经统计分析可得

这两种算法的相对误差均满足

从上面计算结果可以看出,本文中的FFT算法与DFT算法本身的相对误差均小于等于万分之一.
5. 讨论与结论
为了对地震数据采集器的幅频特性进行标准化测试,本文提出了基于FFT和DFT算法的测试方法并编写了测试程序.通过对高精度地震数据采集器的实际幅频特性标定数据的计算处理,得到以下结论:
1)基于DFT的数据积分恢复算法程序采用Visual C#编写,可支持可视化界面操作,在短时间内能够高效率、标准化地完成地震数据采集器幅频特性测试的计算处理;基于FFT谱分析方法采用MATLAB软件编写程序,尽管计算程序简单,但由于不支持可视化界面操作,进行实际标定操作复杂费时.两种算法理论简单,程序都比较简短,且均能高精度地完成标定工作.
2)本文提出的两种算法,其程序均不需要调整参数,直接输入采样数据、采样频率和信号频率即可计算出正弦波最大峰值,具有操作简单、计算速度快和计算精度高的优点,但是必须给出准确的采样频率和信号频率,否则计算结果严重偏离实际值.
3)常用的MATLAB正弦曲线拟合方法尽管程序比较简单,但需要根据计算误差不停地调整程序中拟合函数的各项系数,经过多次调整后才能得到最理想的正弦波函数,从而得出正弦波的最大峰值.该方法耗时长且不方便,优点是无需预知采样频率和信号频率等信息.
4)从实际采集器幅频特性标定数据计算出发,基于DFT的数据积分恢复算法程序更适合实际应用,其次为FFT谱分析方法,最后为MATLAB正弦曲线拟合方法.
本文所提出的这两种算法仅以高精度地震数据采集器、100Hz采样率下的幅频特性标定数据作示例,实际上这两种算法同样适用于处理任何数据采集器以及进行任意采样频率下的幅频特性标定.下一步将在此基础上,进一步对其它类型地震数据采集器幅频特性及地震数据采集器的线性度、 共模抑制比、路际串扰比等其它技术指标进行测试分析.
-
表 1 Q330HRS型高精度数据采集器基本技术指标
Table 1 Main specifications of Q330HRS high precismic data recorder

表 2 Q330HRS采集器幅频特性标定数据(DFT算法)
Table 2 Amplitude-frequency characteristic calibration data of Q330HRS seismic data recorder with DFT method

表 3 两种不同算法采集器幅频特性标定结果
Table 3 Amplitude-frequency characteristic calibration data of Q330HRS seismic data recorder with two method

-
黄爱苹. 1991. 数字信号处理[M]. 北京: 机械工业出版社: 38-85. Huang A P. 1991. Digital Signal Processing[M]. Beijing: China Machine Press: 38-85 (in Chinese).
张德丰. 2010. MATLAB数字信号处理与应用[M]. 北京: 清华大学出版社: 87-120. Zhang D F. 2010. MATLAB Digital Signal Processing and Its Applications[M]. Beijing: Tsinghua University Press: 87-120 (in Chinese).
张宗达, 刘锐, 王勇. 1997. 工科大学数学教程(Ⅰ): 下册[M]. 哈尔滨: 哈尔滨工业大学: 144-203. Zhang Z D, Liu R, Wang Y. 1997. Advanced Mathematics (Ⅰ): 2[M]. Harbin: Harbin Institute of Technology: 144-203 (in Chinese).
-
期刊类型引用(1)
1. 李彩华,滕云田,李小军,汤一翔,王喆,胡星星,张旸. 地震数据采集器非线性指标测试方法及其影响分析. 地震学报. 2019(01): 92-99 .  本站查看
本站查看
其他类型引用(4)




 下载:
下载: