Comparative study among implementations of several free-surface boundaries with perfectly matched layer conditions
-
摘要: 传统的完全匹配层技术是一种能够较为有效地消除边界反射的边界条件,但是当表层为泊松比较高的自由表面时,该技术可能会产生不稳定的现象.针对传统的完全匹配层技术固有的不稳定和掠射情况下吸收效果不佳等缺陷,发展了多轴完全匹配层、卷积完全匹配层以及将两者结合的多轴卷积完全匹配层等3种边界条件.本文介绍了水平自由表面的不同处理方法以及传统、多轴、卷积和多轴卷积等4种完全匹配层条件的原理,通过二维半无限空间模型的交错网格有限差分正演模拟对比,分析了几种自由边界实施方法在这几种完全匹配层条件下的稳定性,并通过提取单道波形与解析解进行对比,定性分析了水平自由表面几种不同处理方法的准确性以及各自的适用条件. 结果表明,泊松比和水平自由表面实施方法对波场模拟效果及其稳定性有重要影响.Abstract: Classical perfectly matched layer (PML) absorbing boundary is certified an efficient method to suppress spurious edge reflections in seismic modeling. However, when modeling Rayleigh waves with the existence of free surface, the classical PML algorithm may become unstable in the case that Poisson’s ratio of the medium is high. On the basis of defects of classical PML, such as its inherent instability and the effects of grazing incidence, multiaxial perfectly matched layer, convolutional perfectly matched layer and multiaxial convolutional perfectly matched layer are developed. Six implementations of planar free-surface boundary conditions and principles of four perfectly matched layer methods are introduced, and forward modeling of 2D half-infinite model using staggered grid finite-difference method are given to study the stability of different methods. Through the comparison of waveform between numerical solution and analytical solution, we can illustrate the accuracy and applicability of these methods in this paper. The results show that Poisson’s ratio and implementations of planar free-surface have an important influence on the effects and stability of wavefield simulation.
-
Keywords:
- PML /
- planar free-surface /
- Poisson’s ratio /
- stability /
- accuracy
-
引言
真实的地下介质空间是半无限大的,而在地震波数值模拟过程中,由于介质模型是有限的,要人为地限定模拟区域,因此需要选取合适的边界条件来消除这种人为的边界反射.Berenger(1994)针对电磁波的传播情况,提出了一种完全匹配层(perfectly matched layer,简写为PML)边界条件;Collino和Tsohka(2001)将这种边界条件应用于弹性波数值模拟方法中,并取得了较好的效果.完全匹配层技术已被证明是一种能够较为有效地消除边界虚假反射的边界条件,但在使用有限差分法进行数值模拟的过程中,传统的PML存在一定的缺陷.Zeng等(2011)指出若地表为有面波存在的自由表面,当介质的泊松比较高时,传统的PML算法会变得不稳定,但这种不稳定现象的产生与自由表面的处理方法有关,不同自由表面的边界条件有不同的稳定性.
地球表面实际上是一个较强的阻抗突变界面,被称为自由表面.有限差分正演的准确性部分取决于自由表面条件的设置(Lan,Zhang,2010).自由表面条件存在多种处理方式.Zahradnik(1995)从理论上证明,采用真空近似方法近似自由表面条件的精度为1阶.Oprsal和Zahradnik(1999)将真空自由表面条件拓展到非均匀网格中,采用阶梯状网格来近似地表形状,计算含有地形起伏的地震波传播过程.Levander(1988)提出了地表法向应力分量反对称的镜像方法,可以较准确地实现水平自由表面.此外,其他学者也提出了一些水平自由表面的处理方法,包括修正有限差分近似(adjusted finite-difference approximation,简写为AFDA)方法(Kristek et al,2002)和特征量方法(Bayliss et al,1986).在水平自由表面的应力镜像方法中,存在多种虚拟层速度值的近似处理方法,张伟(2006)对其进行了阐述.
针对传统PML技术在掠射情况下存在的吸收效果不佳以及固有的不稳定性等缺陷,有关研究人员从不同的角度提出了改进.其中典型的有卷积完全匹配层(convolutional perfectly matched layer,简写为C-PML)和多轴完全匹配层(multiaxial perfectly matched layer,简写为M-PML)以及将两者结合在一起的多轴卷积完全匹配层(multiaxial convolutional perfectly matched layer,简写为MC-PML).
本文将以控制方程为1阶速度-应力方程的水平自由表面处理方法为基础,通过二维半无限大模型的交错网格有限差分正演模拟,对比分析不同处理方法在几种完全匹配层条件下的稳定性,并通过提取单道波形与解析解进行对比,以分析水平自由表面不同处理方法的准确性及各自的适用性.
1. 方法原理
1.1 弹性波交错网格有限差分数值模拟
基于交错网格的有限差分方法在弹性波数值模拟中有着广泛的应用,其主要思想是,将弹性波中的运动微分方程、本构方程与几何方程三者结合,整理出二维各向同性完全弹性介质的1阶速度-应力波动方程形式,其具体表达式如下:

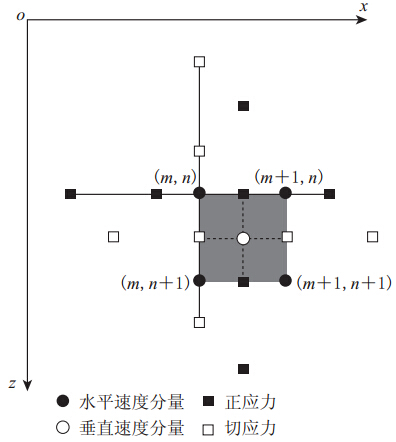
式中:vx和vz为速度分量;σxx,σzz和τxz为应力分量; λ和μ为弹性拉梅常数;ρ为介质密度.式中,速度和应力分量有着很好的空间交错性质,因此Levander(1988)提出采用交错网格将方程离散化.通过图1所示的二维交错网格速度-应力的空间位置分布,将式(1)离散化,从而实现交错网格有限差分正演模拟.
![]() 图 1 二维交错网格速度-应力空间分布图(引自Levander,1988)Figure 1. Spatial stencils of two-dimensional staggered grid for the velocity and stress update Dot and open circle represent horizontal and verical components of velocity,respectively; solid square and hollow square separately represent normal stress and tangential stress
图 1 二维交错网格速度-应力空间分布图(引自Levander,1988)Figure 1. Spatial stencils of two-dimensional staggered grid for the velocity and stress update Dot and open circle represent horizontal and verical components of velocity,respectively; solid square and hollow square separately represent normal stress and tangential stress1.2 水平自由地表的处理方法
在使用交错网格有限差分方法进行数值模拟的过程中,对于空间2N阶精度而言,计算某个点上的导数值需要用到该点两侧N个点的值,而对于靠近边界附近的点来说,会有一部分所需点的值超过所给的模型范围.求取这些点的值的方法可以分为两类:一类是构造虚拟层,虚拟层内的值通过一定的关系给出;另一类是不构造虚拟层,由模型内部已知点的值或者自由表面边界条件求取所需未知量.
水平地表下的应力自由表面条件与速度自由表面条件分别为(张伟,2006)

和

式中,vi,j(i,j=x,y,z)为速度i分量在j方向上的空间导数;σxz,σyz和σzz为应力分量.
由于控制方程为1阶速度-应力方程,同时包含速度和应力分量,因此应该同时满足速度和应力自由表面条件.水平自由表面边界条件的处理方法主要有:
1)直接法,即直接采用2阶精度交错网格有限差分;
2)应力镜像法,即在地表处为零的应力分量具有反对称性质(Levander,1988;Graves,1996;Pitarka,Irikura,1996;Robertsson,1996;Ohminato,Chouet,1997; Gottschammer,Olsen,2001). 设地表位于z=z0,向下为正,则有

其中,应力镜像方法是应力自由表面条件的处理方案.与该方法联合使用的速度自由表面的处理方式为:①对于2阶精度交错网格有限差分,可以将自由表面设置在切应力所在格点,这样不需要位于地表之上格点的速度分量值(Ohminato,Chouet,1997);②在内部使用高阶格式,靠近边界处逐步降阶,最后在自由表面及下一层采用2阶格式.这样计算自由表面下一层时则不需要位于边界之外的速度值(Jastram,Tessmer,1994);③ 在边界处采用2阶格式展开速度自由表面条件,来获得虚拟层内的速度值(Graves,1996);④将虚拟层的速度值取为零的简化处理方法(Robertsson,1996;Pitarka,Irikura,1996);⑤紧致差分格式,即利用自由边界条件及边界处已求出的值,采用内部相同精度的紧致差分格式来计算其余边界格点的速度方向导数. 紧致差分格式的一般形式为(Lele,1992):

式中,αm和βn为紧致差分格式的差分系数,fk+m,z为变量f在格点k+m处z方向的导数值,fk+n为f位于格点k+n的函数值.
1.3 几种完全匹配层的方法原理
完全匹配层技术的实质是坐标变换,传统PML在频率域的变换关系为(王守东,2003)

This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.

C-PML对传统PML的坐标变换关系进行了改进,并通过不分裂的递推卷积实现,可以改善掠射的吸收效果,以x方向为例,其频率域坐标变换关系为(Komatitsch,Martin,2007)

式中αx≥0,κx≥1,二者均为引入的辅助吸收因子.
在时间域,

ψx是记忆变量,可以通过下式递推得到:

其中,bx=exp[-(dx/κx+αx)Δt],ax=dx(bx-1)/[κx(dx+κxαx)],Δt为时间步长.
M-PML从衰减系数的角度对传统PML进行了改进,在几个方向上同时引入衰减系数,以达到稳定的目的,并通过分裂的形式得以实现(以x方向为例)(Zeng et al,2011).

和

分别为PML和M-PML方法衰减因子的选取方式.其中d(x)x和d(x)z为衰减因子;p(z/x)为不同方向衰减因子的比例系数,亦称为稳定性因子,通过调整稳定性因子可使计算结果稳定.
MC-PML则是将M-PML中多个方向同时引入衰减因子的思想借鉴到C-PML的实施过程中,同时保留C-PML的复频移坐标变换关系和不分裂的实现方法.
2. 数值模拟
2.1 不同自由表面方法在几种完全匹配层条件下的稳定性比较
为了验证第一节中提到的6种自由表面边界条件的稳定性,本文设计了一个均匀半空间模型,考虑地表为自由表面进行方法对比测试.计算的几何参数:纵波速度为520 m/s,密度为1500 kg/m3;计算区域为100 m×50 m,匹配层区域宽度为10 m,空间采样间隔为0.1 m×0.1 m,时间采样间隔为0.05 ms;震源主频为50 Hz,位于地表中央.
首先,考虑低泊松比情况. 设模型的泊松比为0.25,即横波速度为300 m/s,对上述6种自由表面处理方法分别进行正演模拟. 以应力镜像和紧致差分方法为例,其模拟结果如图2所示.模拟结果显示,当泊松比较低时,传统PML算法在上述6种自由表面处理方法下都较为稳定.
然后,将上述模型的泊松比设为0.48,即横波速度为102 m/s,同样对上述6种自由表面处理方法分别进行正演模拟. 图3a-f分别给出了传统PML算法在6种自由表面条件下得到的地震记录.
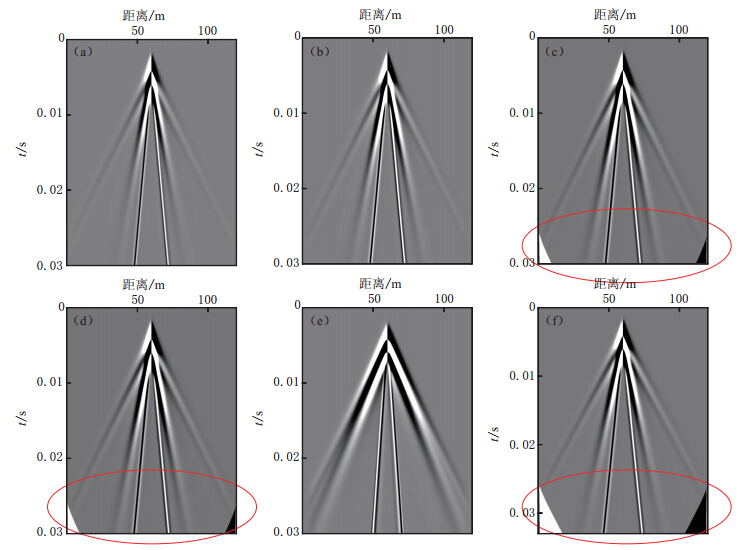
由图3的地震记录对比可知:采用直接法、应力镜像-2阶格式以及应力镜像-虚拟层赋零等3种处理方法时,传统PML算法是稳定的.为了进一步验证该算法在大时间尺度下的稳定性,将模拟时间增加至2s,以排除这几种方法的稳定性与时间的相关性.实验结果表明:在长时间的模拟情况下,采用直接法和应力镜像-2阶格式这两种方法,传统PML算法仍是稳定的;采用应力镜像-虚拟层赋零法时,在约1.9s时刻由于数值溢出而导致计算终止,因此大规模长时间情况下,用该方法处理是不稳定的;而采用应力镜像-降阶、应力镜像-2阶速度展开以及应力镜像-紧致差分这3种方法时,从地震记录的红色区域可以明显地看到不稳定现象,其由于不稳定而溢出的时间分别为170,169和167 ms.
![]() 图 3 地震记录 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-2阶速度展开法;(e)应力镜像-虚拟层赋零法;(f)应力镜像-紧致差分法Figure 3. Seismic records (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and second-order velocity evolving method;(e)Stress image and fictitious layer assigns to zero method;(f)Stress image and compact difference method
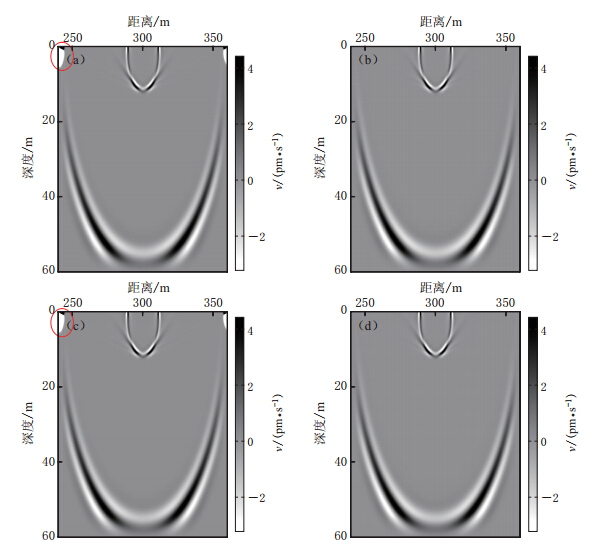
图 3 地震记录 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-2阶速度展开法;(e)应力镜像-虚拟层赋零法;(f)应力镜像-紧致差分法Figure 3. Seismic records (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and second-order velocity evolving method;(e)Stress image and fictitious layer assigns to zero method;(f)Stress image and compact difference method为方便比较不同的完全匹配层条件的稳定性,本文将几种完全匹配层技术在同一种处理方法下的正演模拟结果进行对比.图4给出了泊松比为0.48时采用应力镜像-紧致差分处理方法分别在传统PML,C-PML,M-PML以及MC-PML条件下同一时刻的波场快照.由图4的对比结果可以看出,在该介质模型中,传统PML和C-PML在高泊松比情况下是不稳定的,而M-PML和MC-PML是稳定的.
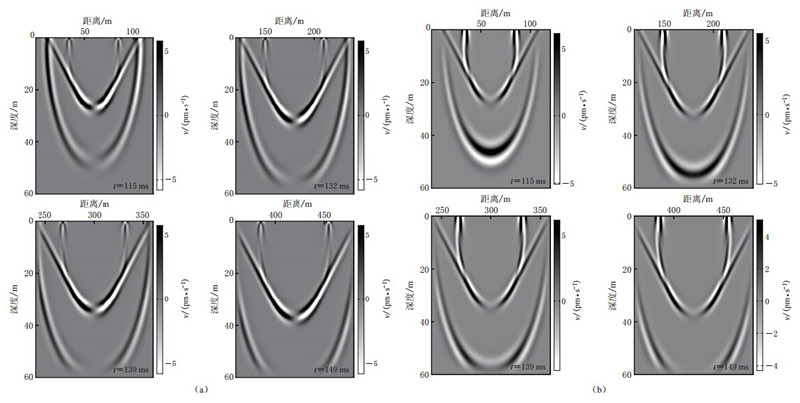
![]() 图 4 传统PML(a)、M-PML(b)、C-PML(c)和MC-PML(d)条件下采用应力镜像-紧致差分法得到的t=139 ms时刻的波场快照(泊松比为0.48). 图中画圈处为不稳定机理Figure 4. Wavefield snapshots computed by stress image and compact difference method when the Poisson’s ratio is 0.48 with PML(a),M-PML(b),C-PML(c) and MC-PML(d)at time instant t=139 ms. The red circle represents the instability
图 4 传统PML(a)、M-PML(b)、C-PML(c)和MC-PML(d)条件下采用应力镜像-紧致差分法得到的t=139 ms时刻的波场快照(泊松比为0.48). 图中画圈处为不稳定机理Figure 4. Wavefield snapshots computed by stress image and compact difference method when the Poisson’s ratio is 0.48 with PML(a),M-PML(b),C-PML(c) and MC-PML(d)at time instant t=139 ms. The red circle represents the instability鉴于图3中采用应力镜像-紧致差分、应力镜像-降阶以及应力镜像-2阶速度展开这3种方法在高泊松比下出现的不稳定问题,本文选取这3种方法不同时刻的波场快照(图5),来进一步分析其正演模拟过程出现不稳定现象的机理.
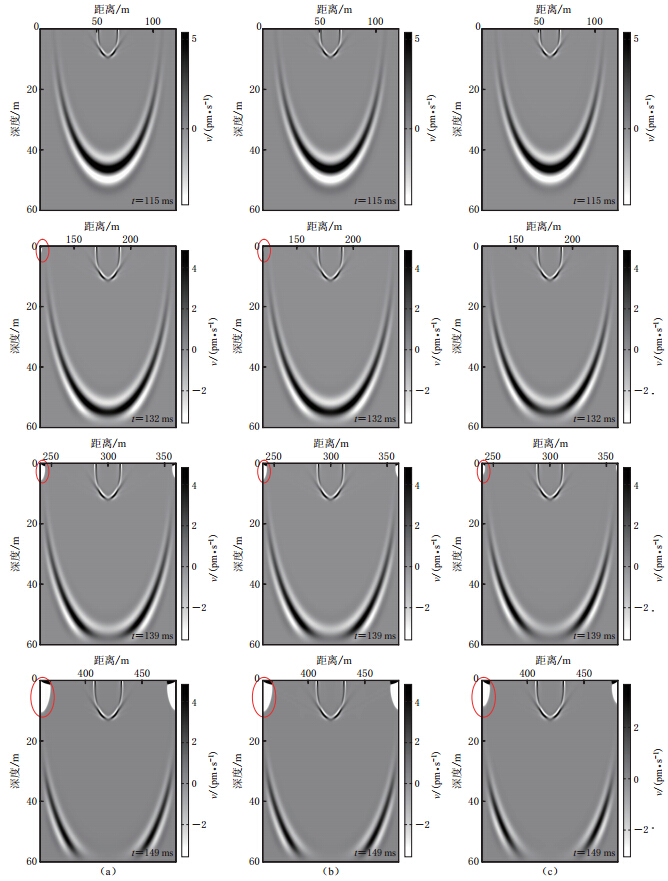
![]() 图 5 传统PML边界条件下泊松比为0.48时t=115,132,139和149 ms时刻的波场快照 (a)应力镜像-紧致差分法;(b)应力镜像-降阶法;(c)应力镜像-2阶速度展开法Figure 5. Wavefield snapshots when the Poisson’s ratio is 0.48 with the classical PML at time instant t=115,132,139 and 149 ms (a)Stress image and compact difference method;(b)Stress image and reduced-order method;(c)Stress image and second-order velocity evolving method
图 5 传统PML边界条件下泊松比为0.48时t=115,132,139和149 ms时刻的波场快照 (a)应力镜像-紧致差分法;(b)应力镜像-降阶法;(c)应力镜像-2阶速度展开法Figure 5. Wavefield snapshots when the Poisson’s ratio is 0.48 with the classical PML at time instant t=115,132,139 and 149 ms (a)Stress image and compact difference method;(b)Stress image and reduced-order method;(c)Stress image and second-order velocity evolving method在图5a-c的波场快照中,t=115 ms时,波传播到底部PML层,并没有引起PML层和计算区域边界的虚假反射; t=132ms时,当波前面到达完全匹配层的左右上角的外边界时,三者均在红色圆圈处出现了数值误差,且图5a和图5b中的数值误差较图5c更为明显;随着波的传播,在t=139 ms和t=149ms的波场快照上,左右上角的数值误差不断地累积.这充分表明,这些情况下PML算法变得不稳定,最终会因为数值溢出而导致计算终止.
由图5的波场快照还可以看到,不稳定现象最先出现在地表自由边界与左右完全匹配层外边界相接触的地方.实验结果表明,将外边界的狄里赫利条件替换成垂直自由表面时,也同样会产生不稳定的现象,究其原因可能是自由表面与左右完全匹配层 物理截断相作用的结果.为了进一步验证不稳定现象产生的原因,本文进行了一系列的模型试算,具体如下:
1)设计一个不带完全匹配层的模型,以研究仅仅自由表面的截断是否会产生不稳定. 实验结果显示没有不稳定现象的出现,这表明产生不稳定现象的原因不是自由表面单独作用的结果.
2)将匹配层的厚度加大,以验证不稳定现象产生的时刻. 实验结果表明,波不是一传入完全匹配层即会产生不稳定,而是当传播到自由表面与完全匹配层的物理截断接触之处,不稳定现象方才发生.
3)为了近一步验证2)中的实验结果,通过改变模型区域的大小和介质的速度来控制波传播的时间. 结果显示,在区域大小和速度均不相同的情况下,不稳定现象产生的时间会发生改变.
通过上述一系列模型试算结果对比可以得出,不稳定现象的产生是自由表面与左右完全匹配层物理截断相互作用的结果,当P-S转换波传播到此位置时才会产生不稳定现象,这可能是不稳定现象最先出现在左右上角的原因.
2.2 不同自由表面条件的准确性对比
2.2.1 均匀半空间模型
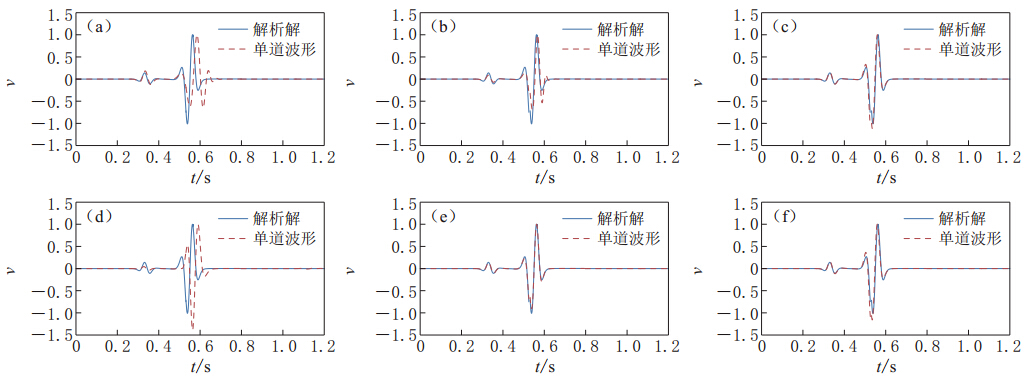
为了讨论上述提及的水平自由表面处理方法在传统PML条件下的 准确性,首先设计了一个地表为自由表面的均匀半空间模型,模型大小为800 m×600 m,纵波速度为1 200 m/s,横波速度为693 m/s,密度为2 000 kg/m3,空间网格间距为2 m,时间步长为0.4 ms,震源位于(0,4 m)处,主频为15 Hz的雷克子波加载在垂直方向的集中力震源,分别采用6种自由表面处理方法进行正演模拟,并选取距离震源(300 m,2 m)的单道波形与解析解(De Hoop,1960;田坤等,2013)进行对比,如图6所示.
![]() 图 6 单道波形(虚线)与解析解(实线)的对比 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-虚拟层赋零法;(e)应力镜像-2阶速度展开法;(f)应力镜像-紧致差分法Figure 6. Comparison of waveforms between numerical(dashed line) and analytical solutions(solid line) (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and fictitious layer assigns to zero method;(e)Stress image and second-order velocity evolving method;(f)Stress image and compact difference method
图 6 单道波形(虚线)与解析解(实线)的对比 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-虚拟层赋零法;(e)应力镜像-2阶速度展开法;(f)应力镜像-紧致差分法Figure 6. Comparison of waveforms between numerical(dashed line) and analytical solutions(solid line) (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and fictitious layer assigns to zero method;(e)Stress image and second-order velocity evolving method;(f)Stress image and compact difference method从图6的对比结果中可以看到,图6c,e和f对应的应力镜像-降阶、应力镜像-2阶速度展开和应力镜像-紧致差分这3种方法与解析解吻合得很好;由图6b可看出,采用应力镜像-2阶格式法,纵波以及面波的前半段能够与解析解有很好地吻合,后半部分有所偏差;而图6a和图6d中,采用直接法和应力镜像-虚拟层赋零的方法,与解析解相比误差较大,究其原因,可能是由于直接法采用的空间精度较低,而虚拟层赋零法忽略了速度自由边界条件的作用所致.
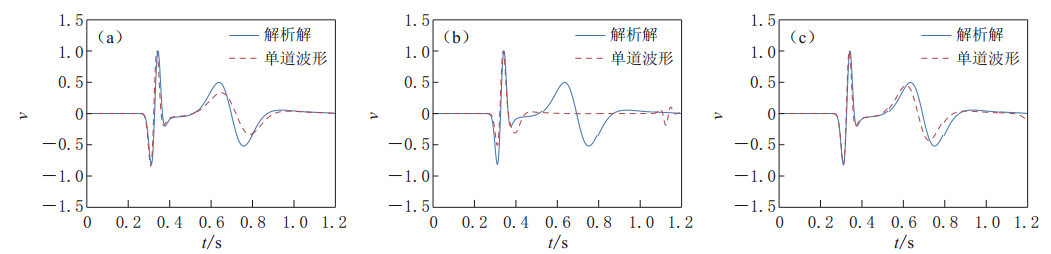
然后,将横波速度变为245m/s,即泊松比为0.48,进行模型试算,结果显示,当泊松比较高时,采用应力镜像-紧致差分法、2阶速度展开法以及降阶法均会出现不稳定的现象,而直接法、应力镜像-虚拟层赋零以及应力镜像-2阶格式等3种方法是稳定的,因此选取这3种方法进行正演模拟得到的单道波形与解析解进行对比,对比结果如图7所示.
由图7可看出,采用直接法、应力镜像-2阶格式法以及虚拟层赋零法,传统PML算法仍是稳定的.通过与解析解的对比可知,采用直接法和应力镜像-2阶格式法,数值解能够与解析解很好吻合,并且应力镜像-2阶格式法比直接法的准确性更高;而采用应力镜像-虚拟层赋零法,虽然算法稳定,但其与解析解偏差较大,准确性较低.
2.2.2 层状模型
设计一个地表为自由表面的双层模型,模型的几何参数:计算区域为100 m×50 m,匹配层宽度为10 m;第一层纵波速度为520 m/s,密度为1 500 kg/m3,深度为25 m;第二层纵波速度为1 000 m/s,密度为1 500 kg/m3;空间采样间隔为0.1 m×0.1 m,时间采样间隔为0.01 ms,震源主频为50 Hz,位于(0,1 m)处.
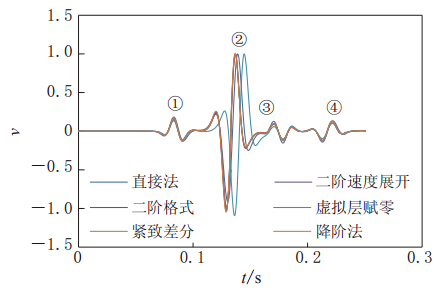
首先,考虑低泊松比的情况,设两层的泊松比均为0.25,即第一层横波速度为300 m/s,第二层横波速度为577 m/s,分别采用1.2节中提及的6种水平自由地表处理方法进行正演模拟.结果显示,对于该层状模型,在低泊松比情况下,采用这6种自由表面处理方法3种算法均是稳定的.为了讨论层状介质中这6种方法在传统PML条件下的准确性,选取距离震源(30 m,0)的单道波形进行了对比,如图8所示.
由图8的波形对比可知,该单道波形中包含直达纵波、面波、反射纵波以及反射横波的信息,采用应力镜像-虚拟层赋零法时,其单道波形与另外5种方法的结果有一定的偏差,可能是由于该方法忽略了速度自由表面条件的影响所致.
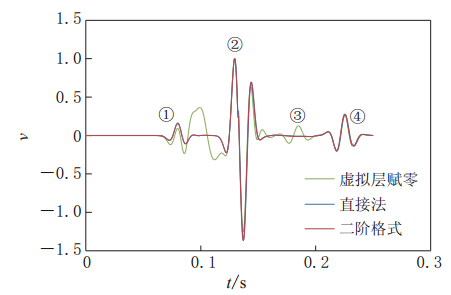
然后,将两层的横波速度分别设为102 m/s和200 m/s,即考虑泊松比为0.48的情况.通过数值模拟结果可知,采用应力镜像-紧致差分法、2阶速度展开法以及降阶法均会出现不稳定现象;而采用直接法、应力镜像-2阶格式法以及虚拟层赋零法,传统PML算法仍是稳定的.
对于3种稳定的算法,本文提取了距离震源(30 m,0)的单道波形进行了对比,如图9所示.由对比结果可知,采用虚拟层赋零法,虽然算法稳定,但其单道波形与另外两种方法的结果存在一定的偏差.
2.3 不同水平自由表面条件总结
通过上述稳定性和准确性的讨论,将传统的PML算法在不同水平自由表面条件下的情况进行总结概括,如表1所示.
表 1 传统PML在不同水平自由表面边界条件下的对比总结Table 1. Comparison among implementations of planar free-surface boundary conditions with the classical PML
由表1可知,不同的自由表面条件,其稳定性和准确性是不同的,因此适用条件也不尽相同.当泊松比较低时,可采用应力镜像-降阶法、2阶速度展开法或紧致差分法,可以在保证稳定性的同时提高模拟的精度;而在泊松比较高时,可采用直接法或者应力镜像-2阶格式法,计算较为简单,也可采用改进的方法,即M-PML或MC-PML技术.实验结果表明,这两种技术可以很好地解决上述3种方法在高泊松比情况下的不稳定问题.在实际处理过程中,需要根据介质情况,结合每种处理方法各自的特点,选择合适的正演模拟方法及边界条件进行数值模拟,从而保证正演模拟结果的稳定性、准确性和有效性.
3. 讨论与结论
本文基于水平自由表面的不同处理方法以及完全匹配层条件的原理,通过二维半无限大模型的交错网格有限差分正演模拟,对比分析了6种自由边界实施方法在PML,M-PML,C-PML和MC-PML等4种完全匹配层条件下的稳定性,并通过提取单道波形与解析解进行对比,分析了水平自由表面不同处理方法的准确性以及各自的适用条件,通过模型试算得到如下认识:
1)泊松比和自由表面处理方法对波场模拟的效果和稳定性具有重要的影响,不同的自由表面方法,其稳定性和准确性不同.在文中论及的6种水平自由表面实施方法中,直接法、应力镜像-2阶格式以及应力镜像-虚拟层赋零这3种处理方法,稳定性较好,但在低泊松比情况下精度较低;而另外3种方法,即应力镜像-降阶法、应力镜像-2阶速度展开法、应力镜像-紧致差分法,在低泊松比情况下的精度较高,但在高泊松比情况下,会出现不稳定现象.
2)同一自由表面处理方法在不同完全匹配层条件下稳定性也有所差异. 传统PML和C-PML算法在高泊松比下是不稳定的,而M-PML和MC-PML算法是稳定的,并且相对传统PML在吸收效果方面也有一定的改进.
3)在实际处理过程中,需要根据研究的出发点和实际的介质情况,结合每种自由表面处理方法的稳定性、准确性以及计算效率等方面的特点,选择合适的方法进行地震波场正演模拟.此外,方法适用范围从水平自由表面向起伏自由表面发展,对进一步解决复杂地表的地震波正演模拟问题有重要意义.
-
图 1 二维交错网格速度-应力空间分布图(引自Levander,1988)
Figure 1. Spatial stencils of two-dimensional staggered grid for the velocity and stress update Dot and open circle represent horizontal and verical components of velocity,respectively; solid square and hollow square separately represent normal stress and tangential stress
图 3 地震记录 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-2阶速度展开法;(e)应力镜像-虚拟层赋零法;(f)应力镜像-紧致差分法
Figure 3. Seismic records (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and second-order velocity evolving method;(e)Stress image and fictitious layer assigns to zero method;(f)Stress image and compact difference method
图 4 传统PML(a)、M-PML(b)、C-PML(c)和MC-PML(d)条件下采用应力镜像-紧致差分法得到的t=139 ms时刻的波场快照(泊松比为0.48). 图中画圈处为不稳定机理
Figure 4. Wavefield snapshots computed by stress image and compact difference method when the Poisson’s ratio is 0.48 with PML(a),M-PML(b),C-PML(c) and MC-PML(d)at time instant t=139 ms. The red circle represents the instability
图 5 传统PML边界条件下泊松比为0.48时t=115,132,139和149 ms时刻的波场快照 (a)应力镜像-紧致差分法;(b)应力镜像-降阶法;(c)应力镜像-2阶速度展开法
Figure 5. Wavefield snapshots when the Poisson’s ratio is 0.48 with the classical PML at time instant t=115,132,139 and 149 ms (a)Stress image and compact difference method;(b)Stress image and reduced-order method;(c)Stress image and second-order velocity evolving method
图 6 单道波形(虚线)与解析解(实线)的对比 (a)直接法;(b)应力镜像-2阶格式法;(c)应力镜像-降阶法;(d)应力镜像-虚拟层赋零法;(e)应力镜像-2阶速度展开法;(f)应力镜像-紧致差分法
Figure 6. Comparison of waveforms between numerical(dashed line) and analytical solutions(solid line) (a)Direct method;(b)Stress image and second-order scheme method;(c)Stress image and reduced-order method;(d)Stress image and fictitious layer assigns to zero method;(e)Stress image and second-order velocity evolving method;(f)Stress image and compact difference method
表 1 传统PML在不同水平自由表面边界条件下的对比总结
Table 1 Comparison among implementations of planar free-surface boundary conditions with the classical PML

-
田坤, 黄建平, 李振春, 李娜, 孔雪, 李庆洋. 2013. 实现复频移完全匹配层吸收边界条件的递推卷积方法[J]. 吉林大学学报: 地球科学版, 43(3): 1022-1032. Tian K, Huang J P, Li Z C, Li N, Kong X, Li Q Y. 2013. Recursive convolution method for implementing complex frequency-shifted PML absorbing boundary condition[J]. Journal of Jilin University: Earth Science Edition, 43(3): 1022-1032 (in Chinese).
王守东. 2003. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 38(1): 31-34. Wang S D. 2003. Perfectly matched layer absorbing boundary of acoustic equation[J]. Oil Geophysical Prospecting, 38(1): 31-34 (in Chinese).
张伟. 2006. 含起伏地形的三维非均匀介质中地震波传播的有限差分算法及其在强地面震动模拟中的应用[D]. 北京: 北京大学地球与空间科学学院: 29-37. Zhang W. 2006. Finite Difference Seismic Wave Modeling in 3D Heterogeneous Media With Surface Topography and Its Implementation in Strong Ground Motion Study[D]. Beijing: School of Earth and Space science, Peking University: 29-37 (in Chinese).
Bayliss A, Jordan K E, Lemesurier B J, Turkel E. 1986. A fourth-order accurate finite-difference scheme for the computation of elastic-waves[J]. Bull Seism Soc Am, 76(4): 1115-1132.
Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetics waves[J]. Journal of Computational Physics, 114(2): 185-200.
Collino F, Tsohka C. 2001. Application of the perfectly matched layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 66(1): 294-307.
De Hoop A T. 1960. A modification of Cagniard's method for solving seismic pulse problems[J]. Appl Sci Res, 8(B): 349-356.
Gottschammer E, Olsen K B. 2001. Accuracy of the explicit planar free-surface boundary condition implemented in a fourth-order staggered-grid velocity-stress finite-difference scheme[J]. Bull Seism Soc Am, 91(3): 617-623.
Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bull Seism Soc Am, 86(4): 1091-1106.
Jastram C, Tessmer E.1994. Elastic modeling on a grid with vertically varying spacing[J]. Geophys Prosp, 42(4): 357-370.
Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 72(5): SM155-SM167.
Kristek J, Moczo P, Archuleta R J. 2002. Efficient methods to simulate planar free surface in the 3D 4(th)-order staggered-grid finite-difference schemes[J]. Studia Geophysica et Geodaetica, 46(2): 355-381.
Lan H Q, Zhang Z J. 2010. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation[J]. J Geophys Eng, 8(2): 275-286.
Lele S K. 1992. Compact finite difference schemes with spectral-like resolution[J]. J Comput Phys, 103(1): 16-42.
Levander A R. 1988. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 53(11): 1425-1436.
Ohminato T, Chouet B A. 1997. A free-surface boundary condition for including 3D topography in the finite-difference method[J]. Bull Seism Soc Am, 87(2): 494-515.
Oprsal I, Zahradnik J. 1999. Elastic finite-difference method for irregular grids[J]. Geophysics, 64(1): 240-250.
Pitarka A, Irikura K. 1996. Modeling 3D surface topography by finite-difference method: Kobe-JMA station site, Japan, case study[J]. Geophys Res Lett, 23(20): 2729-2732.
Robertsson J. 1996. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography[J]. Geophysics, 61(6): 1921-1934.
Zahradnik J. 1995. Simple elastic finite-difference scheme[J]. Bull Seism Soc Am, 85(6): 1879-1887.
Zeng C, Xia J H, Miller R D, Tsoffias G P. 2011. Application of the multiaxial perfectly matched layer (M-PML) to near-surface seismic modeling with Rayleigh waves[J]. Geophysics, 76(3): T43-T52.
-
期刊类型引用(8)
1. 朱旭芳,颜冰,马知远. 浅海舰船地震波场仿真中的边界处理. 国防科技大学学报. 2018(02): 85-90 .  百度学术
百度学术
2. 周敏,武杰. 不依赖于子波的声波多尺度全波形反演方法. 声学技术. 2018(06): 521-527 .  百度学术
百度学术
3. 崔超,黄建平,李振春,廖文远,关哲. 一种基于拟相位信息目标泛函的反射波波形反演方法(英文). Applied Geophysics. 2017(03): 407-418+461 .  百度学术
百度学术
4. 程壮,秦良,张士宽. 矿井超前探测高阶交错网格有限差分数值模拟. 勘察科学技术. 2017(03): 31-34+39 .  百度学术
百度学术
5. 崔超,黄建平,王自颖,国运东. 基于双差的波动方程反射波旅行时反演方法. 石油地球物理勘探. 2017(04): 734-742+624 .  百度学术
百度学术
6. 黄建平,杨宇,李振春,田坤,李庆洋. 基于M-PML边界的Lebedev网格起伏地表正演模拟方法及稳定性分析. 中国石油大学学报(自然科学版). 2016(04): 47-56 .  百度学术
百度学术
7. 黄建平,刘培君,李庆洋,李振春,雍鹏. 一种棱柱波逆时偏移方法及优化. 石油物探. 2016(05): 719-727 .  百度学术
百度学术
8. 李力,唐汝琪,魏伟. 黏弹性VTI煤层介质超声波传播模型建立与分析. 煤炭学报. 2015(12): 2987-2994 .  百度学术
百度学术
其他类型引用(6)




 下载:
下载: