Influence of lining tunnel on sub-ground motion for incident plane SH wave excitation
-
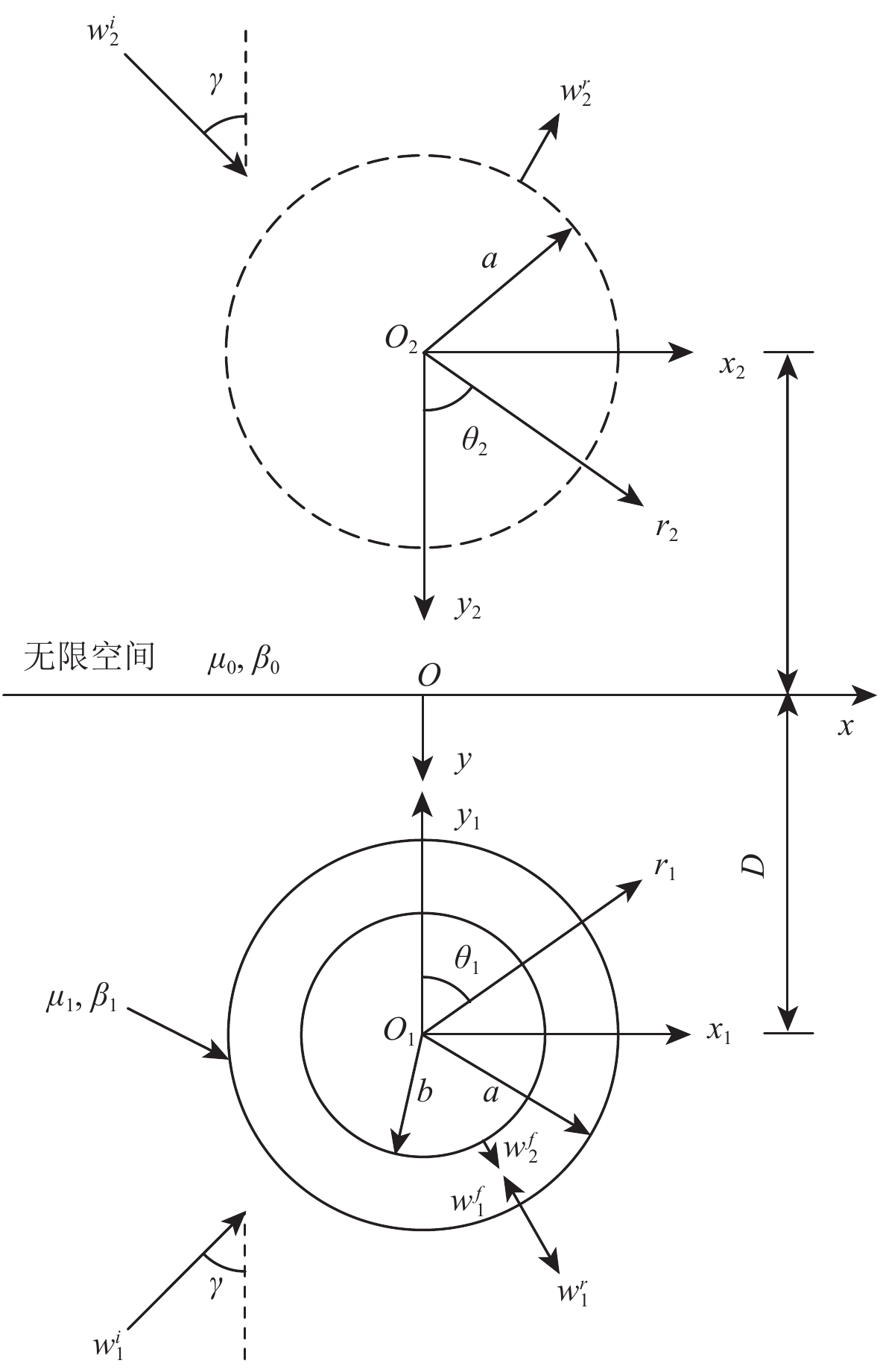
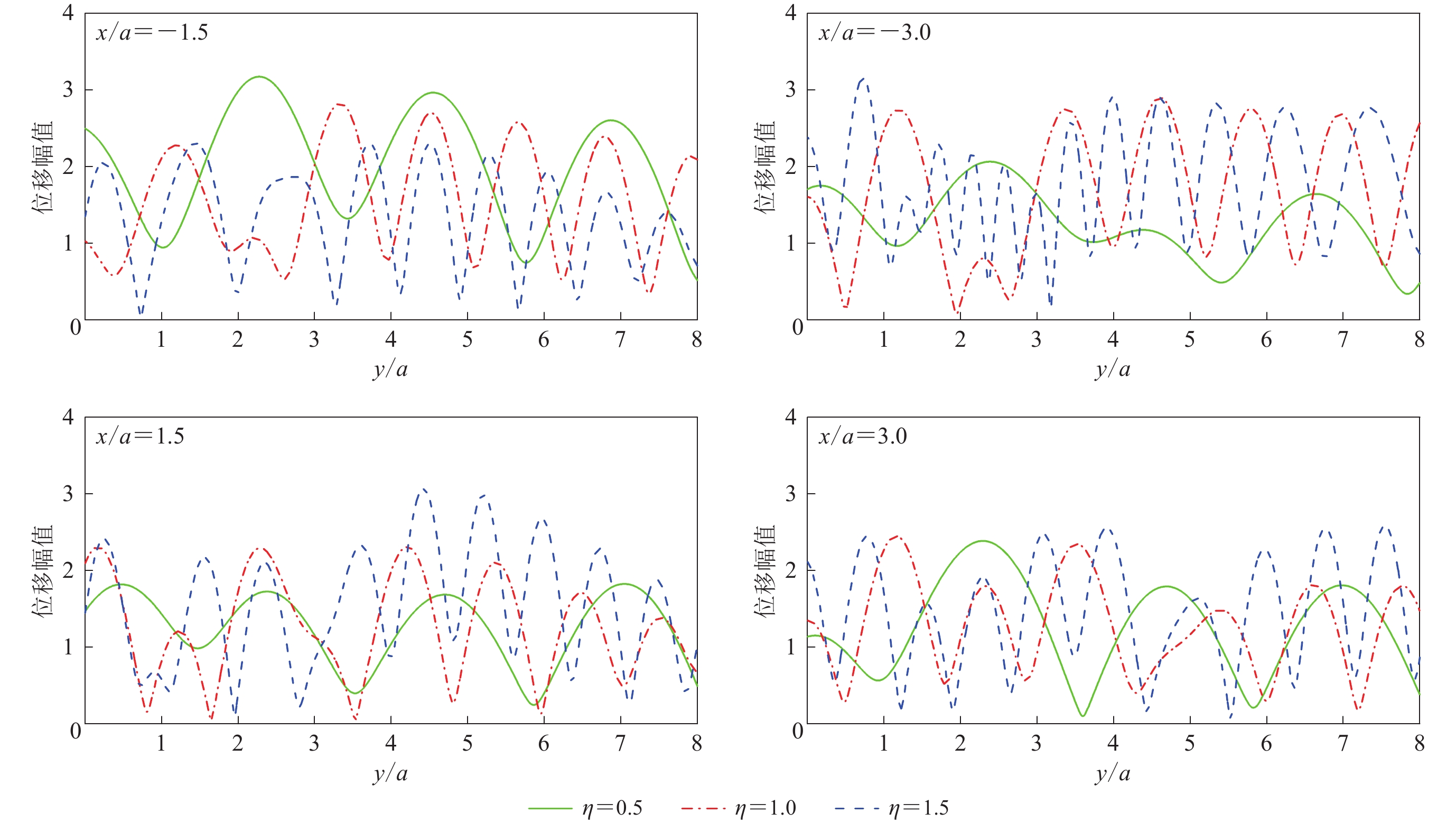
摘要: 以地下隧道对附近场地动力特性的影响为研究目标,基于弹性波动理论,利用波函数展开法和镜像法,分析了弹性半空间中圆形衬砌隧道对平面SH波入射产生的散射问题,得到了地下圆形衬砌隧道附近场地位移的级数解答。通过数值算例分析了地下圆形衬砌隧道对场地动力响应的影响,重点考察了SH波入射角度、入射频率和隧道埋深、衬砌刚度对隧道周围土体动力响应随深度变化的影响规律。结果表明,地下隧道对沿线场地的地下地震动影响显著。Abstract: Taking the influence of underground tunnel on the dynamic characteristics of the nearby site as the researched objective, this paper analyzed the scattering of incident plane SH wave resulted from circular lining tunnel in elastic half space by using the wave function expansion method and the image theory based on the elastic wave theory, and then obtained the series solution of the site displacement near the underground circular lining tunnel. Numerical examples are used to analyze the influence of the underground circular tunnel on the dynamic response of the site, i.e., the influence of SH wave incidence angle, incident frequency, tunnel depth and lining stiffness on the dynamic response of soil around the tunnel with depth. The results show that underground tunnel has a significant impact on sub-ground motion along the site.
-
Keywords:
- plane SH wave /
- circular lining tunnel /
- image method /
- sub-ground motions
-
-
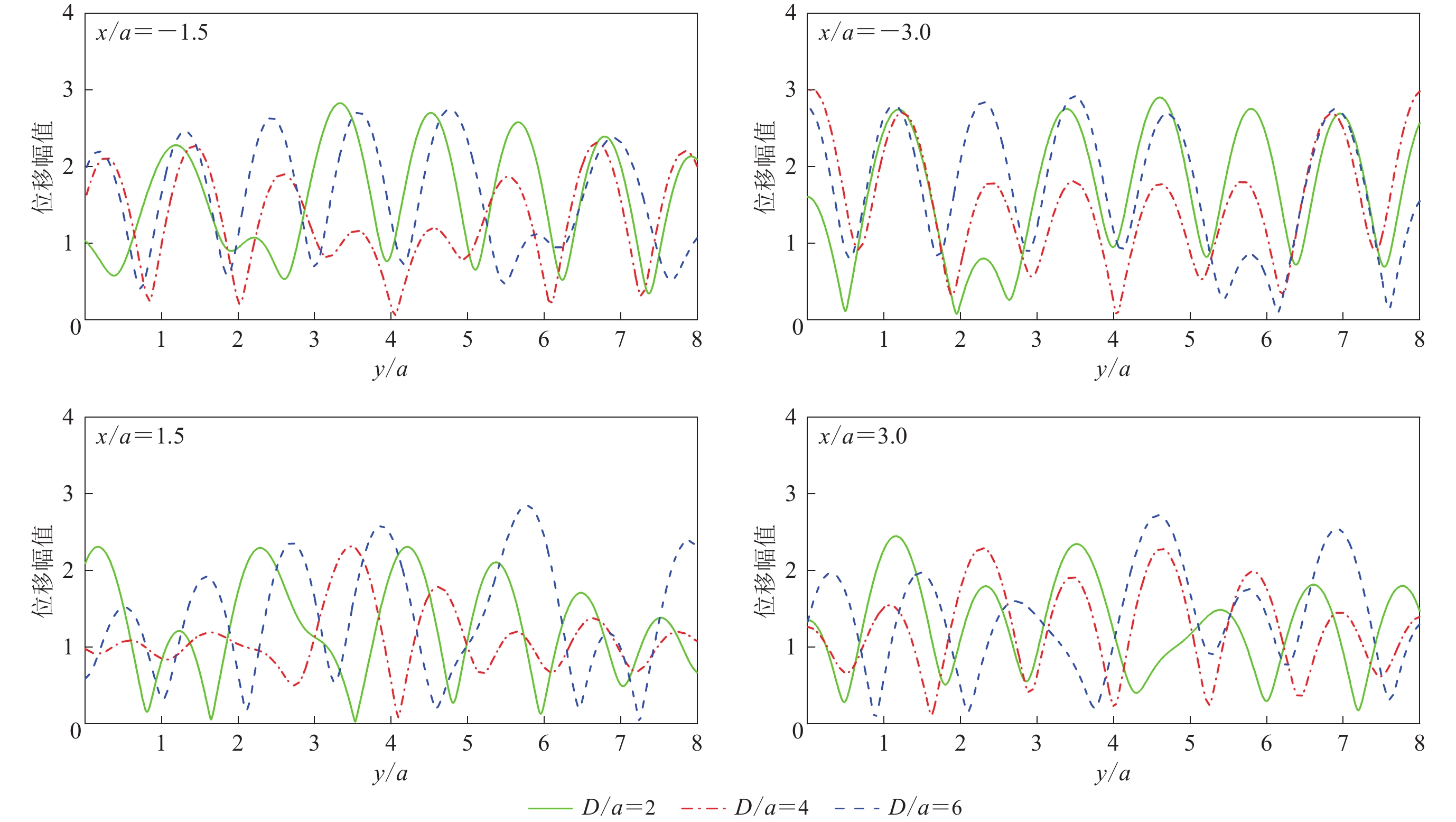
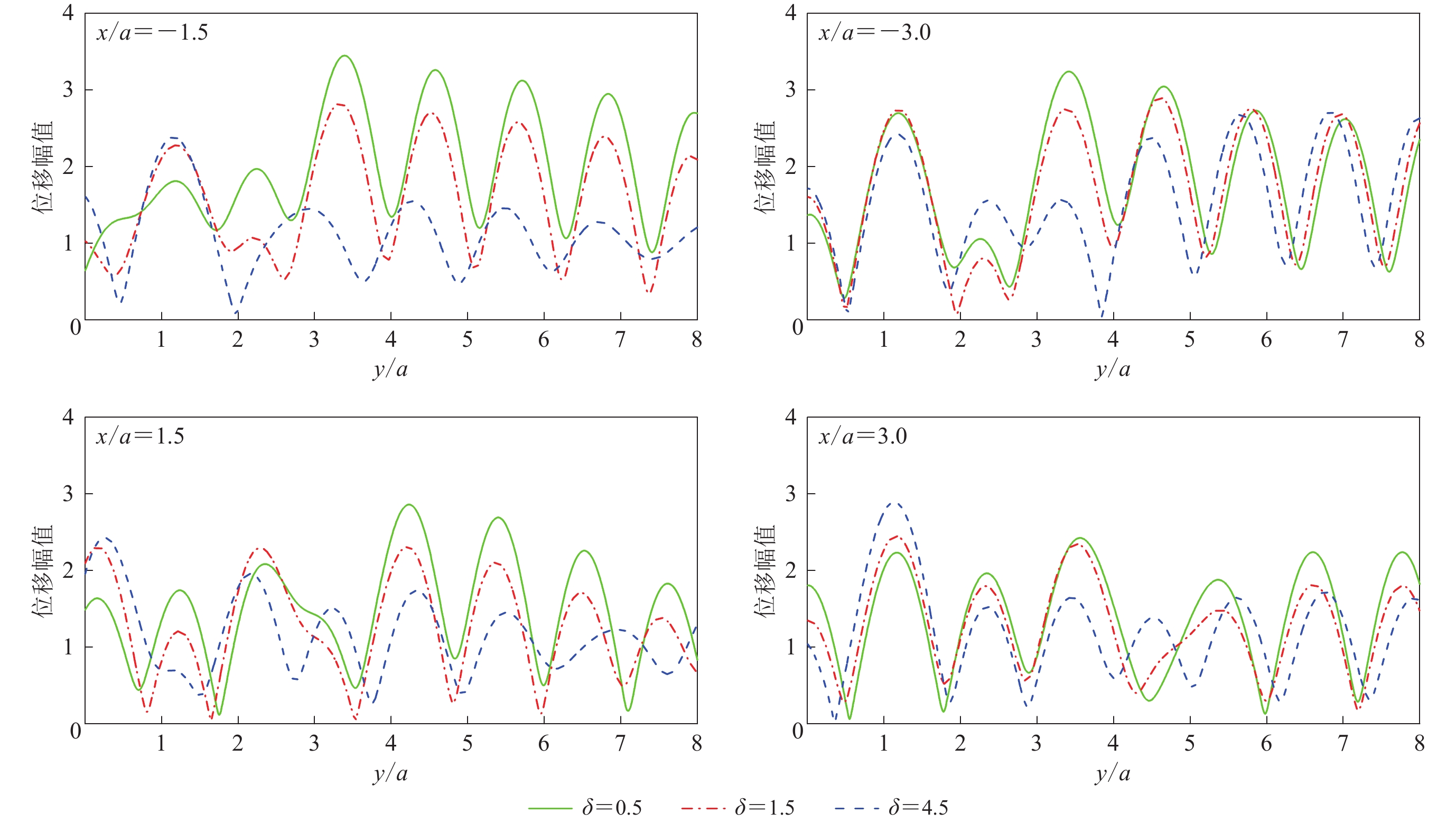
表 1 距地表6a深度范围内隧道左右两侧最大地下位移幅值
Table 1 The maximum amplitude of underground displacement on both sides of tunnel within a depth of 6a from surface
入射角/° 地下位移幅值 x/a=−3.0 x/a=−1.5 x/a=1.5 x/a=3.0 0 2.66 2.79 2.79 2.66 30 2.90 2.83 2.31 2.45 60 3.30 2.37 2.64 2.61 90 3.31 3.94 3.37 3.01 -
付佳,梁建文,杜金金. 2016. 平面SH波激励下的土–隧道动力相互作用的解析解[J]. 岩土工程学报,38(4):588–598. Fu J,Liang J W,Du J J. 2016. Analytical solution of dynamic soil-tunnel interaction for incident plane SH wave[J]. Chinese Journal of Geotechnical Engineering,38(4):588–598 (in Chinese).
梁建文,张浩,Lee V W. 2004. 地下洞室群对地面运动影响问题的级数解答:P波入射[J]. 地震学报,26(3):269–280. doi: 10.3321/j.issn:0253-3782.2004.03.006 Liang J W,Zhang H,Lee V W. 2004. A series solution for surface motion amplification due to underground group cavities:Incident P waves[J]. Acta Seismologica Sinica,26(3):269–280 (in Chinese).
梁建文,纪晓东,Lee V W. 2005a. 地下圆形衬砌隧道对沿线地震动的影响( Ⅰ ):级数解[J]. 岩土力学,26(4):520–524. Liang J W,Ji X D,Lee V W. 2005a. Effects of an underground lined tunnel on ground motion ( Ⅰ ):Series solution[J]. Rock and Soil Mechanics,26(4):520–524 (in Chinese).
梁建文,纪晓东,Lee V W. 2005b. 地下圆形衬砌隧道对沿线地震动的影响( Ⅱ ):数值结果[J]. 岩土力学,26(5):687–692. Liang J W,Ji X D,Lee V W. 2005b. Effects of an underground lined tunnel on ground motion ( Ⅱ ):Numerical results[J]. Rock and Soil Mechanics,26(5):687–692 (in Chinese).
Alielahi H,Adampira M. 2016. Effect of twin-parallel tunnels on seismic ground response due to vertically in-plane waves[J]. Int J Rock Mech Min Sci,85:67–83. doi: 10.1016/j.ijrmms.2016.03.010
de Barros F C P,Luco J E. 2010. Seismic response of a cylindrical shell embedded in a layered viscoelastic half-space. Ⅱ :Validation and numerical results[J]. Earthq Eng Struct Dyn,23(5):569–580.
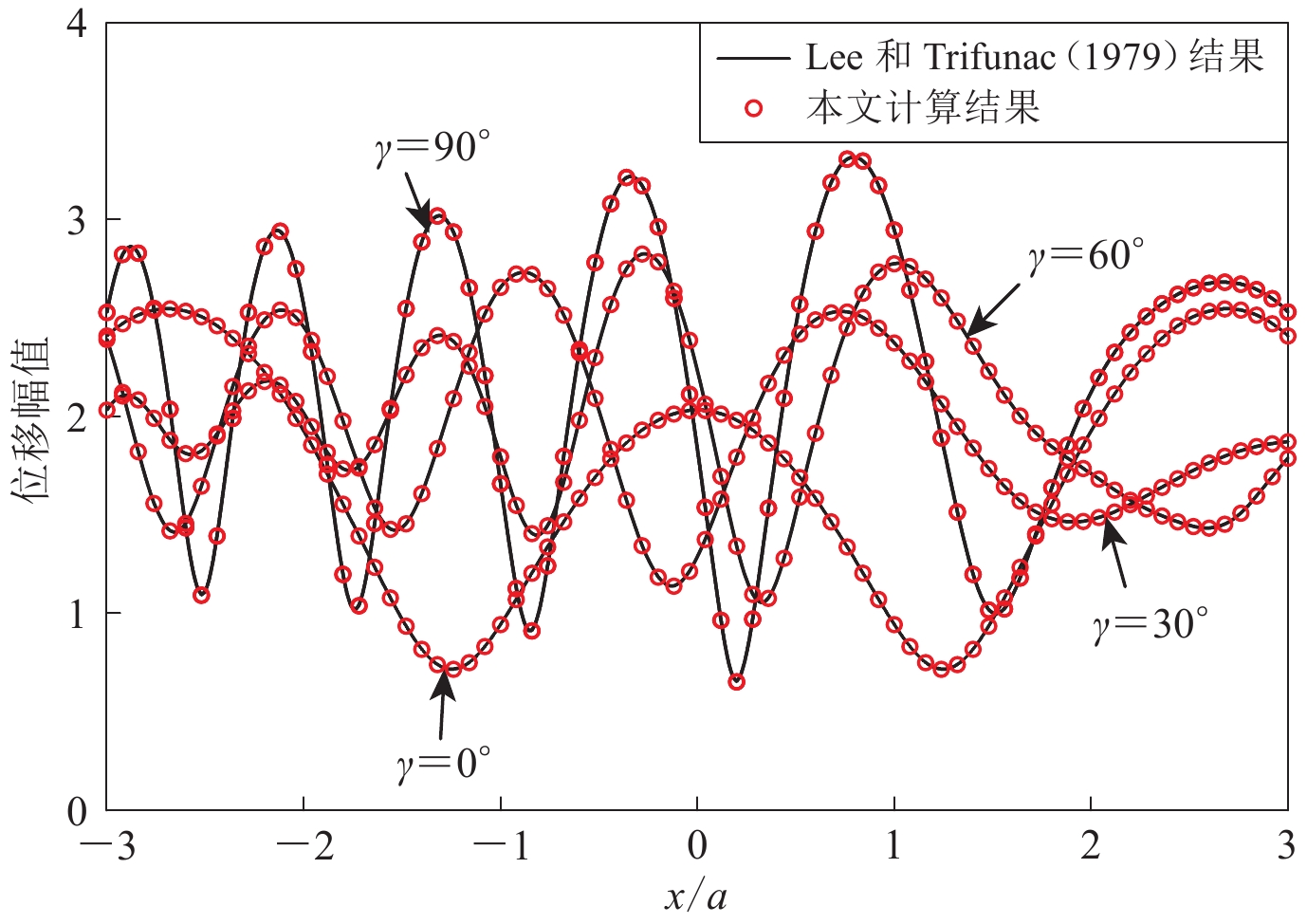
Lee V W,Trifunac M D. 1979. Response of tunnels to incident SH-waves[J]. J Eng Mech Div,105(4):643–659.
Lee V W,Karl J. 1992. Diffraction of SV waves by underground,circular,cylindrical cavities[J]. Soil Dyn Earthq Eng,11(8):445–456. doi: 10.1016/0267-7261(92)90008-2
Lee V W,Karl J. 1993. On deformation near a circular underground cavity subjected to incident plane P waves[J]. Eur J Earthq Eng,7(1):29–35.
Liang J W,Zhang H,Lee V W. 2003. A series solution for surface motion amplification due to underground twin tunnels:Inci-dent SV waves[J]. Earthq Eng Eng Vibrat,2(2):289–298. doi: 10.1007/s11803-003-0012-x
Liang J W,Chen J Q,Ba Z Y. 2012. 3D scattering of obliquely incident SH waves by a cylindrical cavity in layered elastic half-space ( Ⅰ ):Methodology and verification[J]. Earthquake Science,34(6):785–792.
Liang J W,Chen J Q,Ba Z Y. 2013. 3D scattering of obliquely incident SH waves by a cylindrical cavity in layered elastic half-space ( Ⅱ ):Numerical results and analysis[J]. Earthquake Science,35(2):173–183.
Liu Q J,Zhao M J,Wang L H. 2013. Scattering of plane P,SV or Rayleigh waves by a shallow lined tunnel in an elastic half space[J]. Soil Dyn Earthq Eng,49:52–63. doi: 10.1016/j.soildyn.2013.02.007
Liu Z X,Liu L. 2015. An IBEM solution to the scattering of plane SH-waves by a lined tunnel in elastic wedge space[J]. Earthquake Science,28(1):71–86. doi: 10.1007/s11589-015-0112-5
Liu Z X,Wang Y R,Liang J W. 2016. Dynamic interaction of twin vertically overlapping lined tunnels in an elastic half space subjected to incident plane waves[J]. Earthquake Science,29(3):185–201. doi: 10.1007/s11589-016-0155-2
Luco J E,de Barros F C P. 2010. Seismic response of a cylindrical shell embedded in a layered viscoelastic half-space. Ⅰ :Formulation[J]. Earthq Eng Struct Dyn,23(5):553–567.
Morse P M,Feshbach H,Condon E U. 1954. Methods of theoretical physics,parts Ⅰ & Ⅱ [J]. Phys Today,7(12):15–16. doi: 10.1063/1.3061460
Mow C C,Pao Y H. 1973. The diffraction of elastic waves and dynamic stress concentrations[J]. J Appl Mechan,40(4):213–219.
Narayan J P,Kumar D,Sahar D. 2015. Effects of complex interaction of Rayleigh waves with tunnel on the free surface ground motion and the strain across the tunnel-lining[J]. Nat Hazards,79(1):479–495. doi: 10.1007/s11069-015-1853-0
Oliaei M,Alitalesh M. 2015. Ground motion amplification due to underground cavities subjected to incident SV and P in-plane waves[J]. Sci Iran,22(5):1703–1711.
Parvanova S L,Dineva P S,Manolis G D,Wuttke F. 2014. Seismic response of lined tunnels in the half-plane with surface topography[J]. Bull Earthq Eng,12(2):981–1005. doi: 10.1007/s10518-013-9546-0
Xu H,Li T B,Li L Q. 2011. Research on dynamic response of underground circular lining tunnel under the action of P waves[J]. Appl Mech Mater,99/100:181–189. doi: 10.4028/www.scientific.net/AMM.99-100




 下载:
下载: