Earthquake detection using convolutional neural network and its optimization
-
摘要: 本文以西昌台阵观测的8 321次近震数据为例，详细介绍了利用深度卷积神经网络检测地震的数据处理流程，包括数据预处理、模型训练、波形长度、网络层数、学习率和概率阈值等关键参数对检测结果的影响，并将训练得到的最优模型，应用于事件波形和连续波形的检测。研究表明，数据预处理和数据增强可以提升模型的检测精度和抗干扰能力。用于模型训练的波形窗口长度可近似于S-P到时差的最大值。不同网络层数（5—8层）的检测结果差别不大。对于地震检测，学习率设为10−4—10−3较为合适。卷积神经网络检测出的地震数量与选择的概率阈值有关，通过绘制精确率-召回率变化曲线，可以为选择合适的概率阈值提供参考。本文为进一步利用深度学习算法提高地震检测效果提供了参考。Abstract: Earthquake detection is the key step of automatic processing such as earthquake quick report and earthquake early warning. In recent years, the use of deep learning algorithm to detect earthquakes has developed rapidly. However, there are few detailed researches on data processing flow and neural network parameter optimization. Taking 8 321 near earthquake data observed by Xichang array as an example, this paper introduces in detail the data processing flow of detecting earthquakes by using the deep convolution neural network, such as data preprocessing, model training, waveform length, network layers, learning rate and probability threshold on the detection results. Then we detect the continuous waveform with the optimal model. Our research shows that data preprocessing, data augmentation can improve the detection accuracy and anti-interference ability of the model. The length of waveform window used for model training can be approximated to the maximum value from arrival time difference between S- and P- wave. The detection results of different network layers （5—8 layers） are similar. For seismic detection, it is more appropriate to set the learning rate as 10−4—10−3. The earthquakes detected by convolution neural network are related to the probability threshold. By drawing the tradeoff curve of precision with recall rate, it can provide a reference for selecting the appropriate probability threshold. This paper provides an important reference for further study of earthquake detection with deep learning algorithm.
-
Keywords:
- deep learning /
- convolutional neural network /
- earthquake detection /
- model training /
- Xichang array
-
引言
近年来，全球地震台站数量迅速增长。据美国地震学研究联合会统计，最近20年，全球地震台站数量由300个增加至上万个，地震数据量由1 T快速增加至近600 T。目前，我国正在实施国家地震烈度速报与预警工程。未来2—3年，中国大陆的地震台站数量将由1 300个增加至15 000个左右。随着地震台站数量的增加，地震监测能力提升，区域台网记录到的地震数量也成倍增长。尤其是随着页岩气开采、地热资源利用和水库蓄水等工业活动的开展，诱发地震也逐渐增加。以美国中部为例，随着大规模的页岩气开采，2009年前后M≥3.0地震数量由每年的25次增加至360多次。
地震目录和震相到时数据是区域地震台网的重要产出之一。当前地震台站密度越来越高，数据量日益庞大，人工处理地震数据的效率越来越难以满足地震行业发展的需求，迫切需要发展处理大规模地震数据的高效算法。在传统的地震检测算法中，虽然STA/LTA（Allen，1978；Earle，Shearer，1994）易于实现，计算效率高，但对信噪比较低的地震事件检测效果较差，而且阈值参数需要根据不同台站的背景噪声水平进行单独调整才能达到最佳性能（蒋策等，2018；杨旭等，2019）。Baer和Kradolfer （1987）通过将包络函数和动态信号阈值结合到特征函数中，对STA/LTA方法进行了改进。此外，地震学家还发展了包括自回归（Sleeman，van Eck，1999）和高阶统计量（Saragiotis等，2002；Baillard等，2014）等多种地震检测算法。基于波形相似性发展起来的模板匹配技术（Gibbons，Ringdal，2006；Peng，Zhao，2009），通过计算地震波形与模板的互相关系数来估计两者的相似程度，检测地震事件。该方法可以识别出数倍于人工处理的地震目录，但需要预先确定模板事件，计算效率较低，难以用于地震数据实时处理中。如果地震模板不完备，可能会导致检测出的地震目录具有系统偏差。
最近两年，利用深度学习方法检测地震在国内外得到迅速发展。Perol等（2018）使用具有8个卷积层的神经网络，利用俄克拉何马州3个地震台站记录的2 918次地震，训练得到了卷积神经网络（convolutional neural network，缩写为CNN）模型，这一模型可以达到与自相关算法和指纹相似度阈值检测法FAST （Yoon et al，2015）相近的检测能力，且检测效率有显著提升，但是没有拾取震相到时。Ross等（2018a）利用南加州近20年的地震数据进行训练，将CNN用于P波、S波的震相检测中，除了可以较为精确地拾取P波、S波到时，还可以对P波的初动极性进行准确分类，并在2016年加利福尼亚州孟买海滩震群中取得了较好的应用效果。Zhu和Beroza （2018）将用于图形分割的U型网络（U-net）引入到地震检测和震相拾取，并用全卷积网络完成了波形到分类概率的映射，训练得到了PhaseNet模型，可以对不同仪器类型和数据质量的波形完成准确的P波，S波震相拾取，其震相拾取精度要高于长短窗和自回归拾取方法。Zhou等（2019）采用卷积神经网络（CNN）和递归神经网络（recurrent neural network，缩写为RNN）相结合的算法，针对汶川地震余震波形数据生成训练集，训练神经网络，对于地震事件的识别精度以及P波，S波震相的标识精度优于传统检测方法。Wang等（2019）开发了PickNet算法，高效准确地拾取地震P波和S波到时。赵明等（2019）发展了Pg，Sg震相识别与到时拾取的U型网络算法，使用汶川余震和首都圈地震台网记录的样本进行训练和测试，在命中率、均方根误差等指标上均优于STA/LTA和峰度分析方法。刘芳等（2020）结合台阵策略，提出了台阵辅助震相拾取方法，并将其应用于内蒙古台网的数据处理中。
尽管利用深度学习检测地震取得了很多进展，但由于该方法涉及网络模型构建、地震和噪声数据集建立、数据预处理、参数调试、性能评估等多个环节，目前公开发表的论文，对于数据处理和参数调优缺乏较为系统的梳理。本文拟以西昌台阵观测的地震数据作为训练数据集，利用卷积神经网络训练模型，通过比较神经网络结构、数据预处理过程和关键参数优化，训练得到了最优模型，并检测了西昌台阵2018年4月份的连续波形，为后人开展相关研究提供了重要参考。
1. 数据
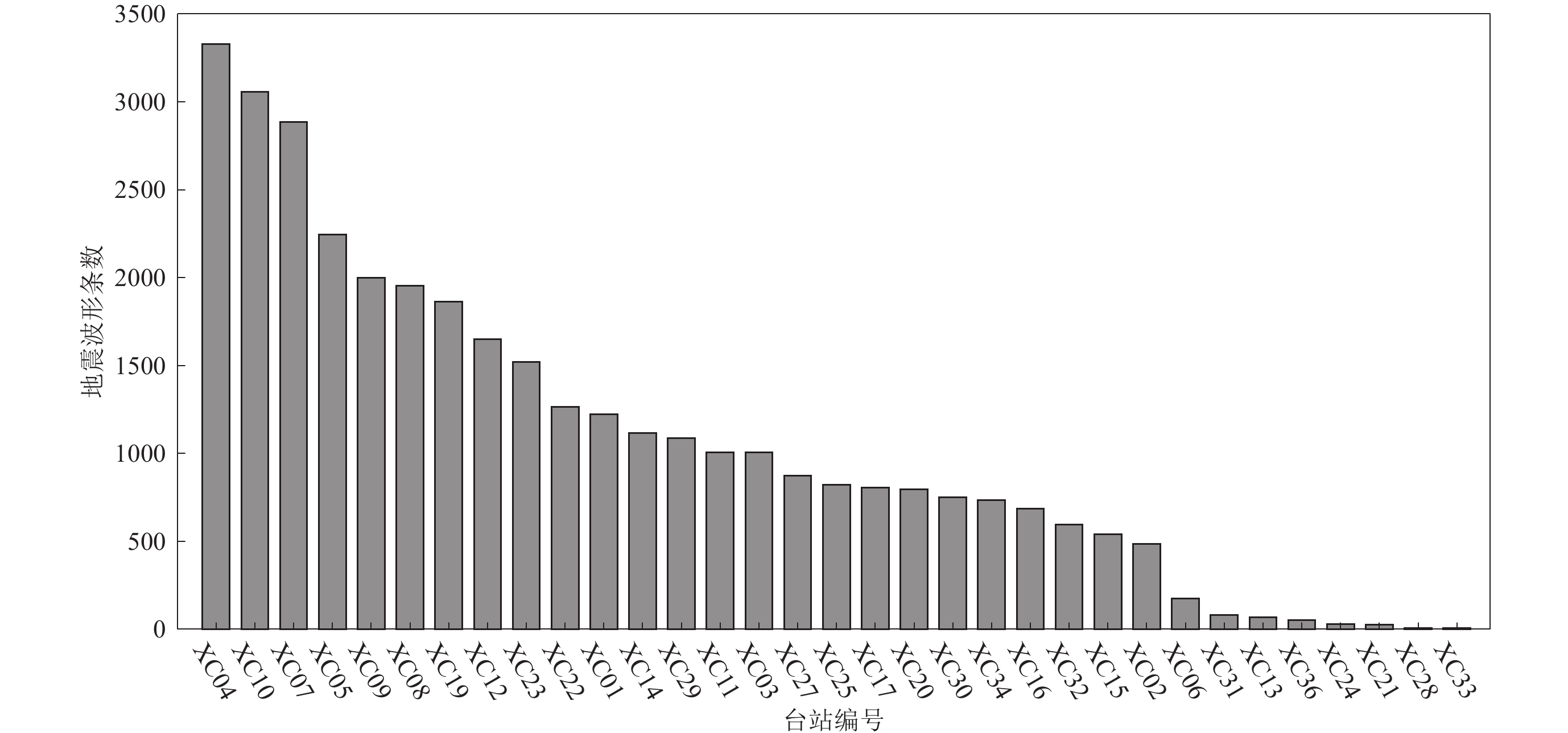
为加强对危险活动断裂带的监测研究，中国地震局地球物理研究所自2013年1月在川西安宁河—则木河断裂带布设了由30套宽频带流动地震台组成的西昌台阵，台阵覆盖范围约200 km×100 km （图1）。本研究以西昌台阵2013年1月至2017年3月记录到的8 321次近震作为数据集，共42 700条事件波形。P，S到时数据由人工拾取，采样率为100 Hz。地震分布如图1所示。训练使用的最小地震震级为ML1.1，最大震级为ML5.0，多数地震的震级小于ML2.0。数据集分为训练集、验证集和测试集。验证集随机挑选2013年4月、8月，2014年6月、12月，2015年2月、8月和2016年10月共929次地震、5 030条事件波形。测试集挑选2017年1—3月份602次地震、2 999条事件波形。剩下的34 671条事件波形作为训练集。地震噪声数据集选取为发震时刻的前45 s至30 s。图2是各个台站的训练集波形数量。
2. 方法
卷积神经网络是一类具有深度结构的前馈神经网络，本研究采用卷积神经网络训练模型，实现地震的检测。卷积神经网络的基本组成包括输入层、隐含层、输出层，隐含层包含卷积层、池化层和全连接层。卷积层对输入数据进行特征提取，卷积层参数包括卷积核大小、步长和补零（padding），三者共同决定了卷积层输出特征图的尺寸。在卷积层进行特征提取后，输出的特征图传递至池化层进行特征选择和信息过滤。全连接层的作用则是对提取的特征进行非线性组合以得到输出。
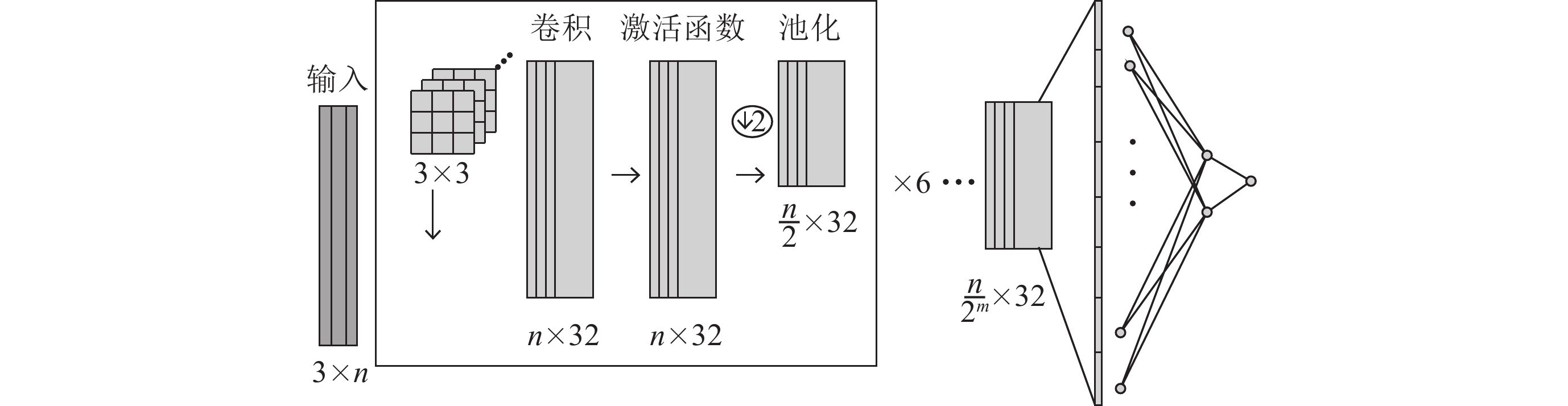
本文采用的卷积神经网络模型框架如图3所示。卷积层主要由三个模块组成：卷积、激活函数和池化。卷积核相当于一个滤波器，用于提取前一层的局部特征。卷积层的运算使得神经网络可以检测到输入样本不同位置的局部特征。我们采用了6个卷积层，每层使用了32个大小为3的卷积核来提取特征。为保持完整的边界信息，使卷积层的输入和输出维度一致，本文采取补零方法，在数据点边缘填充初值为0的数据点。激活函数使用ReLU函数。池化操作可以减少参数的数量，从而改善网络性能并避免过拟合（Krizhevsky et al，2012）。本文采用最大池化方法（max pooling）。最后一个卷积层的输出通过全连接层和softmax函数映射到分类概率，较大的概率对应模型预测的类别。具体如图3所示：
CNN的输入是三通道波形，长度可以根据事件波形的S-P窗口设定。假设每层的输入数据是具有c个通道的二维张量X，每个通道有N个数据点。卷积核W的维度为k×c×f，其中k和f分别表示卷积核大小和输出通道的大小。第f个通道、第n个神经元的输出值yn，f可表示为
${y_{n{\text{，}}f}} {\text{＝}} \sum\limits_{j {\text{＝}} 0}^{c {\text{－}} 1} {\sum\limits_{i {\text{＝}} 0}^{k {\text{－}} 1} {{{W}}_{i{\text{，}}j}^f} } {{{X}}_{n {\text{＋}} i{\text{，}}j}}{\text{，}}$
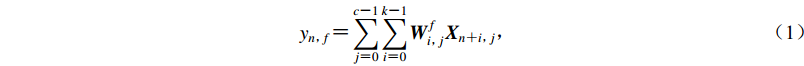
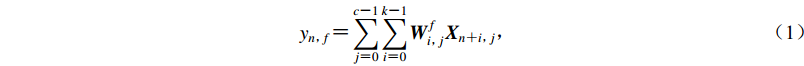
(1) 式中y为大小为（N－k＋1）×f的张量，W是卷积核的权重。
激活操作是在卷积输出上相应地应用非线性函数。常用的激活函数是线性整流函数ReLu （Nair，Hinton，2010），即
$ {y}_{n{\text{，}}f}'{\text{＝}}\max (0{\text{，}}{y}_{n{\text{，}}f}){\text{，}} $
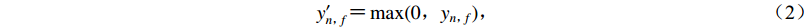
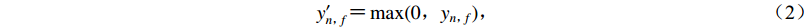
(2) 经过激活操作，最后通过最大池化层在相邻两个神经元中取最大值作为池化层的输出，即
${Y_{n{\text{，}}f}} {\text{＝}} \max (y_{n{\text{，}}f}'{\text{，}}y_{n {\text{＋}} 1{\text{，}}f}').$
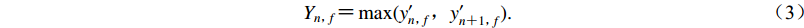
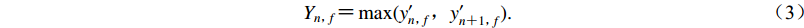
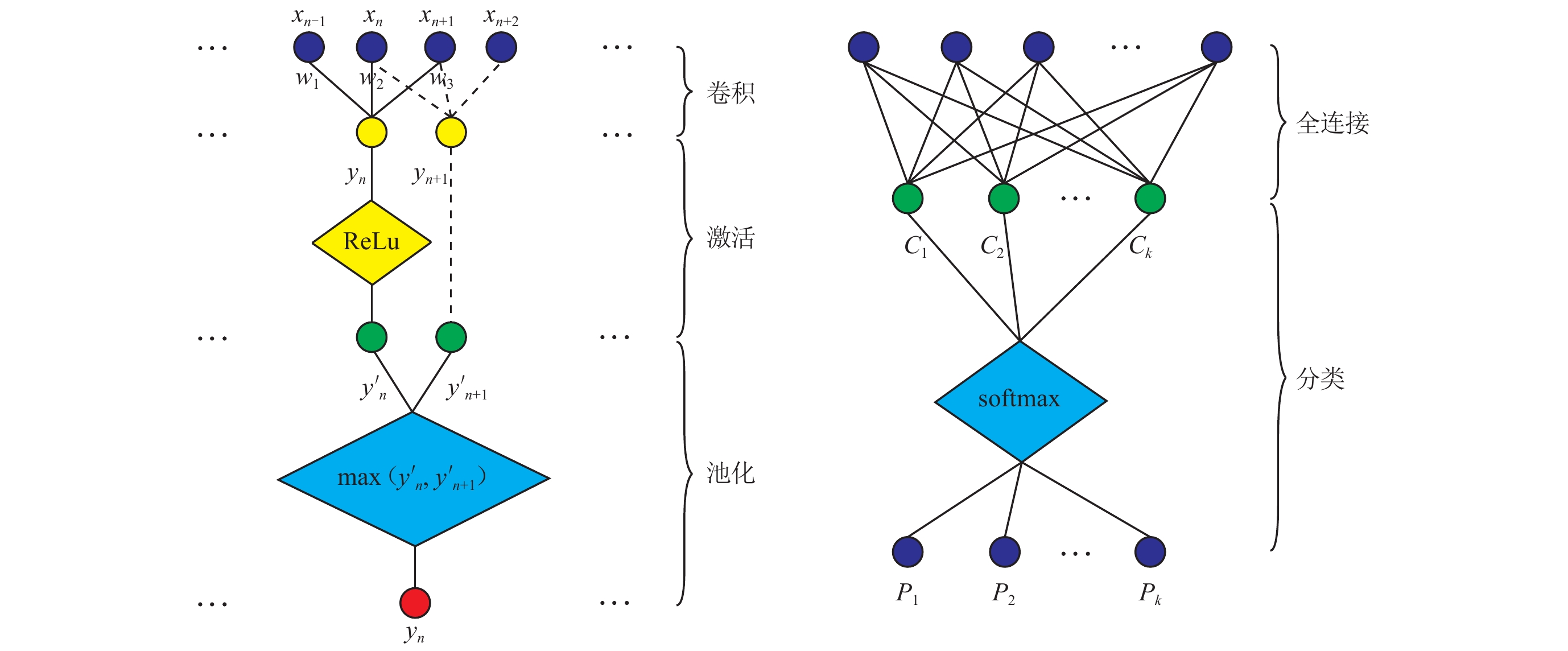
(3) 由于每层的降采样（池化层）操作，最后一个卷积层的输出是一个二维张量，大小为（n/26）×32。图4是一个卷积层的示例。
![]()
图 4 卷积、池化、全连接层局部示意图Figure 4. Schematic diagram of convolution，pooling and fully connected layers本文中使用的损失函数L根据式（4）计算（Ng，2004），采用Adam算法进行优化（Kingma et al，2015）。
$L {\text{＝}} \frac{1}{B}\sum\limits_{j {\text{＝}} 0}^{B {\text{－}} 1} {\sum\limits_{i {\text{＝}} 0}^{K {\text{－}} 1} {{q_{i{\text{，}}j}}\cdot \log ({p_{i{\text{，}}j}}} }) {\text{＋}} \lambda \sum {\left\| W \right\|} _2^2{\text{，}}$
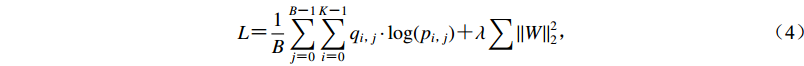
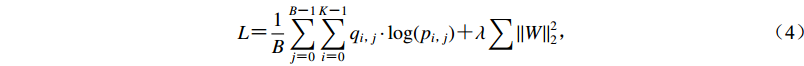
(4) 式中，B为“事件”和“噪声”样本的批量大小，K为分类数，p和q分别为预测概率和真实的标签，λ为L2正则化系数。本研究中B设为128，λ设为10−4。
3. 模型训练与地震检测
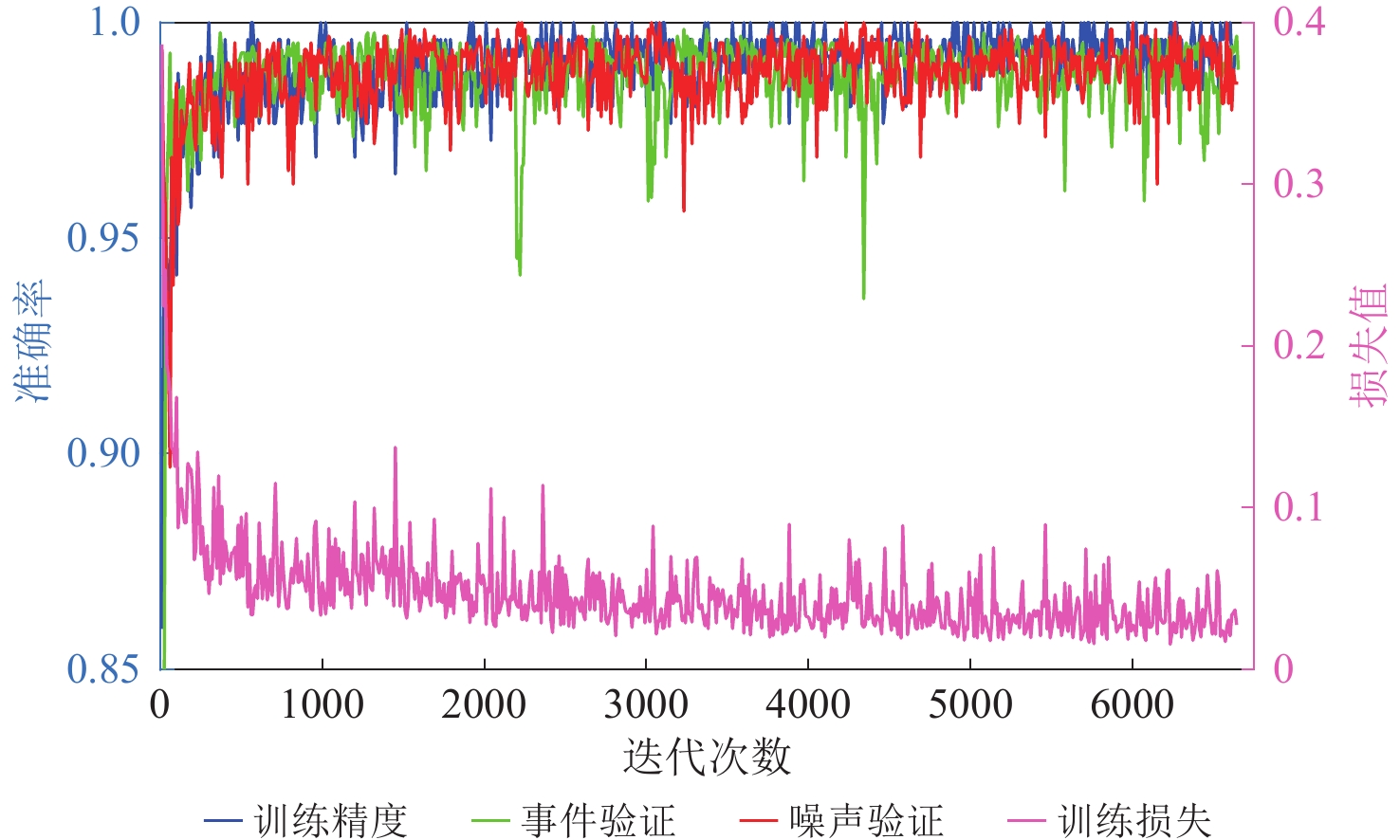
本文使用34 671条事件波形作为原始训练集，波形长度为15 s，其中P波前4 s，P波后11 s。参考Zhu和Beroza （2018）、Zhou等（2019）的数据预处理方法，我们对原始波形数据进行去均值、去倾斜、振幅归一化和1 Hz高通滤波。为了增加训练数据集，还采用增加高斯噪声的方法，以扩展训练数据集。最终训练集包含17万左右的地震事件波形，噪声波形与地震事件波形的比例接近1 ∶ 1。本文中算法基于TensorFlow库实现，模型训练约24个周期（epoch），共迭代6 500次。训练及测试结果如图5所示。在训练集上训练完第一个周期后训练精度达到95%。在验证集上地震的识别正确率随着训练次数的增加而稳步上升。
![]()
图 5 训练和验证曲线Figure 5. The training accuracy，validation accuracy for events and noise and loss function curves深度学习中常选择精确率P、召回率R、准确率A和F1值作为模型性能的评价指标（Powers，David，2011），其定义为
$P {\text{＝}} \frac{{T_{\rm{P}}}}{{T_{\rm{P}} {\text{＋}} F_{\rm{P}}}}{\text{，}}$
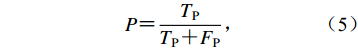
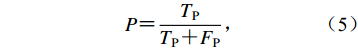
(5) $R {\text{＝}} \frac{{T_{\rm{P}}}}{{T_{\rm{P}} {\text{＋}} F_{\rm{N}}}}{\text{，}}$
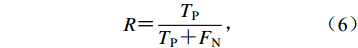
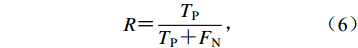
(6) $A {\text{＝}} \frac{{T_{\rm{P}} {\text{＋}} T_{\rm{N}}}}{{T_{\rm{P}} {\text{＋}} T_{\rm{N}} {\text{＋}} F_{\rm{P}} {\text{＋}} F_{\rm{N}}}}{\text{，}}$
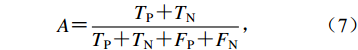
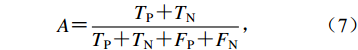
(7) $F_1 {\text{＝}} 2\frac{{P {\text{×}} R}}{{P {\text{＋}} R}}{\text{，}}$
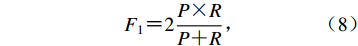
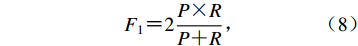
(8) 式中，TP为真正例（即将真实的地震检测为地震）的数量，TN为真反例（即将噪声检测为噪声）的数量，FP为假正例（即将噪声检测为地震）的数量，FN为假反例（即将地震检测为噪声）的数量。当卷积神经网络对输入窗口的检测概率超过50%时则认为检测正确。
4. 参数优化
利用深度学习检测地震涉及网络模型构建、地震和噪声数据集建立、数据预处理、参数优化和性能评估等多个步骤，每一步都对最终的检测结果有影响。本部分对训练数据准备、数据预处理、数据增强、训练窗口长度、网络层数、学习率以及检测概率阈值设置及其影响进行了详细分析。
4.1 数据预处理
连续波形记录中包含了多种地震信号和噪声，对于震级较小或者信噪比较低的地震事件，肉眼也难以识别。在数据中常存在奇异样本，会导致网络训练时间增加，并可能引起网络无法收敛。为改进这种情况，可以对输入信号的振幅进行归一化，使所有样本的均值接近于0或与其均方差相比很小。本文对原始数据进行的预处理包括去均值、去线性趋势、振幅归一化及1 Hz高通滤波。
图6是预处理前后的训练结果对比。从图中可以看出，随着训练精度的提高，在验证集上的准确率难以达到80%，然而噪声的准确率从一开始就很高（图6a）。这表明，如果不作预处理，检测效果会较差。这是因为原始数据可能存在信噪比较低的波形，尤其是对于流动台站而言，其噪声水平一般高于固定台站。也有可能是数据中存在奇异样本，增加了网络训练时间，而且还无法准确地获取地震震相特征，因此对地震和噪声无法作出准确的分类。经过预处理后，在验证集上的检测效果得到明显改善，随着训练精度的提高，验证集上的准确率也随之提高（图6b）。
![]()
图 6 预处理前后的训练和验证曲线Figure 6. Training and validation accuracy curves before and after data preprocess4.2 训练集规模
深度学习通常需要大量的数据进行训练。采用不同数量的数据集训练模型，检测结果也会不同。本文利用不同数量的训练集进行模型训练，训练集地震数量分别为1 334，3 422，6 790，训练集的窗口长度为15 s，并通过数据增强扩充数据集。然后在测试集上评估准确率、精确率、召回率和F1。从表1可以看到，随着训练集数量的增加，准确率、精确率、召回率和F1值都在增加，表明使用更大的训练集可以提高模型性能和泛化能力。
表 1 利用不同规模训练集训练得到的CNN模型检测结果对比Table 1. Comparison of CNN model detection results from different training sets编号 训练集
地震次数训练集地震
波形条数检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 1 1 334 6 595 2 882 2 937 97.02% 96.10% 97.89% 96.99% 2 1 334×3 19 785 2 924 2 936 97.70% 97.50% 97.89% 97.69% 3 1334×6 39 570 2 925 2 938 97.75% 97.53% 97.96% 97.75% 4 3 422 17 465 2 910 2 957 97.82% 97.03% 98.58% 97.79% 5 6 790 34 671 2 929 2 957 98.13% 97.67% 98.59% 98.13% 6 6 790×5 173 355 2 938 2 972 98.53% 97.97% 99.09% 98.53% 注：×号表示数据增强的倍数。测试集中的地震波形条数和噪声波形条数均为2 999条。 深层神经网络结构中含有大量可训练参数，如果数据集较少，训练过程中经常会出现过拟合现象。使用更多的训练数据，可以防止过拟合并增强模型的泛化能力。但在实际训练过程中，能获取到的数据是有限的。为了解决训练数据不足的问题，通常采用数据增强方法，比如拉伸、压缩、加噪声、滑动窗等。我们对原始数据添加高斯噪声，噪声强度为波形数据的标准差乘以0—0.5之间的随机数，通过数据增强将1 334次地震的训练集扩增了3倍和6倍，测试集上的检测结果列于表1。数据增强后，准确率、召回率和F1值都有提升。对于CNN模型未检测出的地震，我们分析了其随震中距、震级和信噪比的关系，发现未检测到的地震多数信噪比低于1.5，震中距在50 km以上所占比例较高，但与震级无明显相关性。
4.3 训练波形长度
不同的地震台网，其台网孔径、台站间距和地震分布可能存在较大差别。对于地震检测而言，在构建训练数据集时，应根据地震事件的持续时间截取完整的波形，使其包含完整的P波和S波波列。如果训练窗口过短，模型中可能无法包含S波的特征；反之，如果波形过长，则会引入较多的噪声特征。
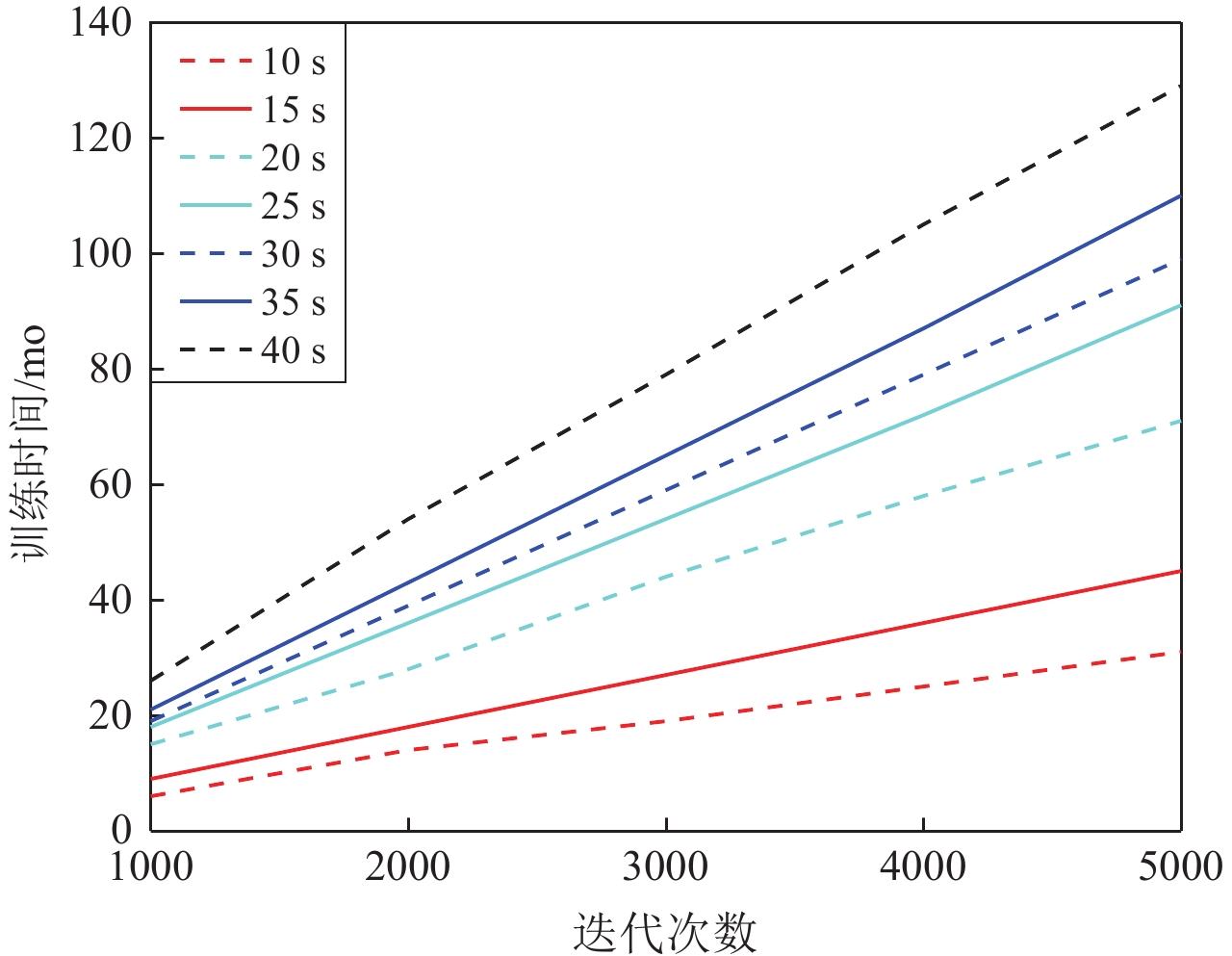
P波和S波到时差可以用来指导训练窗口长度的选取。西昌台阵观测范围大概为200 km×100 km，震中距多数小于100 km。本文分析了西昌台阵8 321次地震的P波和S波到时差，大多数小于20 s （图7）。为测试窗口长度对模型训练和检测结果的影响，我们采用相同的训练集，分别选取10，15，20，25，30，35和40 s的窗长，截取地震事件波形，进行模型训练和测试，结果列于表2。从表2可以看出，15 s窗口的准确率、召回率和F1值较其它窗口长度更高，且使用15 s窗口的训练时间也比其它窗口短（图8）。
表 2 采用不同窗长的训练集训练得到的CNN模型检测结果对比Table 2. Comparison of CNN model detection results by training sets with different window lengths窗口长度/s 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 10 2 904 2 950 97.60% 96.83% 98.34% 97.58% 15 2 929 2 957 98.13% 97.67% 98.57% 98.12% 20 2 920 2 944 97.77% 97.37% 98.15% 97.76% 25 2 904 2 948 97.57% 96.83% 98.27% 97.54% 30 2 900 2 944 97.43% 96.70% 98.14% 97.41% 35 2 895 2 959 97.60% 96.53% 98.64% 97.57% 40 2 904 2 954 97.67% 96.83% 98.47% 97.64% ![]()
图 8 不同窗长的训练步数与训练时间的关系Figure 8. Relationship between training step and training time for different window lengths4.4 P波前窗口长度
目前的训练数据和测试数据，多数研究人员都采用了同样的窗口。比如用于训练的事件波形，如果截取了P波到时前4 s的数据，那么用于测试的数据也采用相同的窗口设置。这对于检测截取好的事件波形可能比较合适，但是当检测连续波形数据时，由于P波、S波可能会位于检测窗口的任意位置，因此可能会影响检测效果。
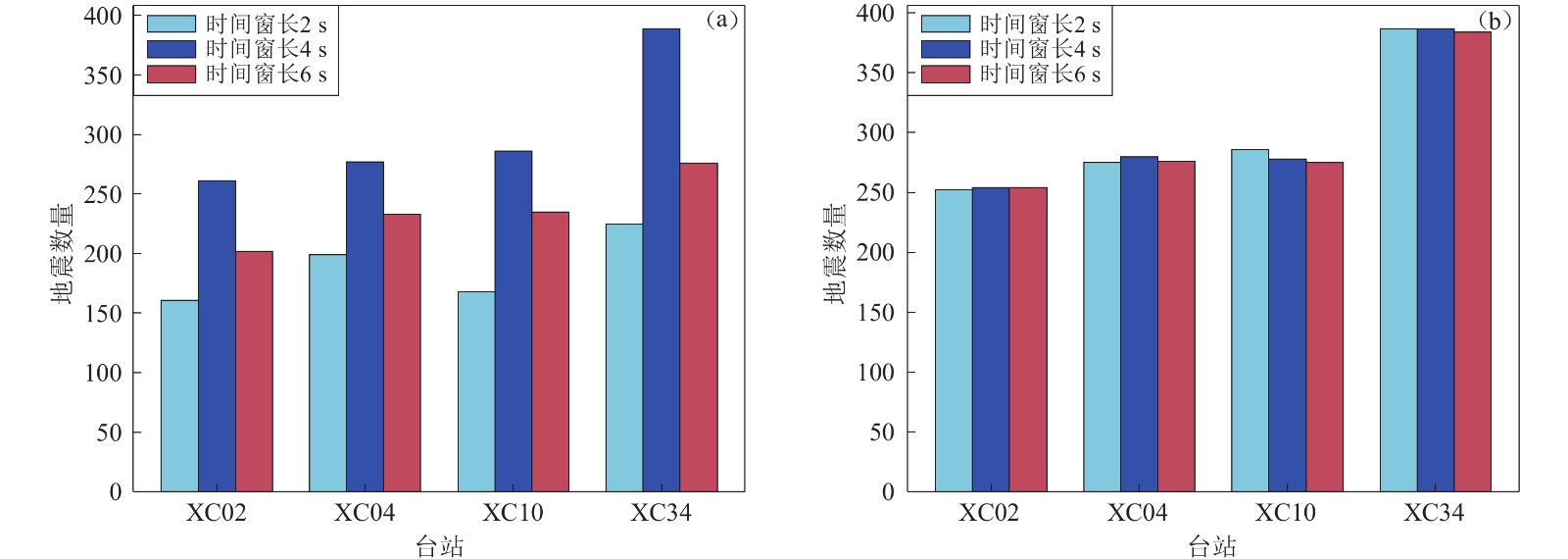
为了分析P波到时前窗口长度对检测结果的影响，在测试集中分别以P波前2，4，6 s的位置作为窗口的起始时间，使用训练好的最优模型进行检测。图9a显示，当截取P波到时前4 s波形时，检测出来的地震最多。以XC34台站为例，当P波前窗口长度为4 s时检测出的地震数量约为2 s时的1.5倍。这表明训练集中P波到时是否固定对检测结果有重要影响。由于在检测连续波形时，P波、S波出现的位置是不确定的，因此训练集中P波到时在窗口中的位置最好为随机值。为此，我们对训练集中的P波到时位置添加0—7.5 s的随机值，即P波会位于15 s训练窗口中0—7.5 s的随机位置。利用新训练得到的模型，对同样的测试集进行检测，可以看出当P波前的窗口长度不同时（图9b），检测结果未出现明显差异，表明P波前窗口长度采用随机值可以提高检测效果。
![]()
图 9 P波到时前不同窗长的检测结果（a） P波到时前窗长为4 s；（b） P波到时前窗长为0—7.5 s的随机值Figure 9. Detection results of different window lengths before the P-wave arrival（a） The window length before P-wave arrival is 4 s；（b） The window length beforeP-wave arrival is a random varying between 0 and 7.5 s4.5 学习率
学习率是指在优化算法中更新网络权重的幅度大小，指导我们通过损失函数的梯度变化调整网络权重的超参数。学习率控制着基于损失梯度调整神经网络权值的速度。学习率越小，损失梯度下降的速度越慢，收敛的时间更长；学习率过大，则可能导致模型不收敛，损失值上下震荡（Wilson，Martinez，2003）。对于地震检测的网络模型训练，学习率一般取值为0.001，0.000 1 （Ross et al，2018b；李安，2019）。随着迭代次数的增加，损失函数缓慢下降，曲线相对平滑，最终收敛在损失函数很低的水平上，表明选择的学习率较好。
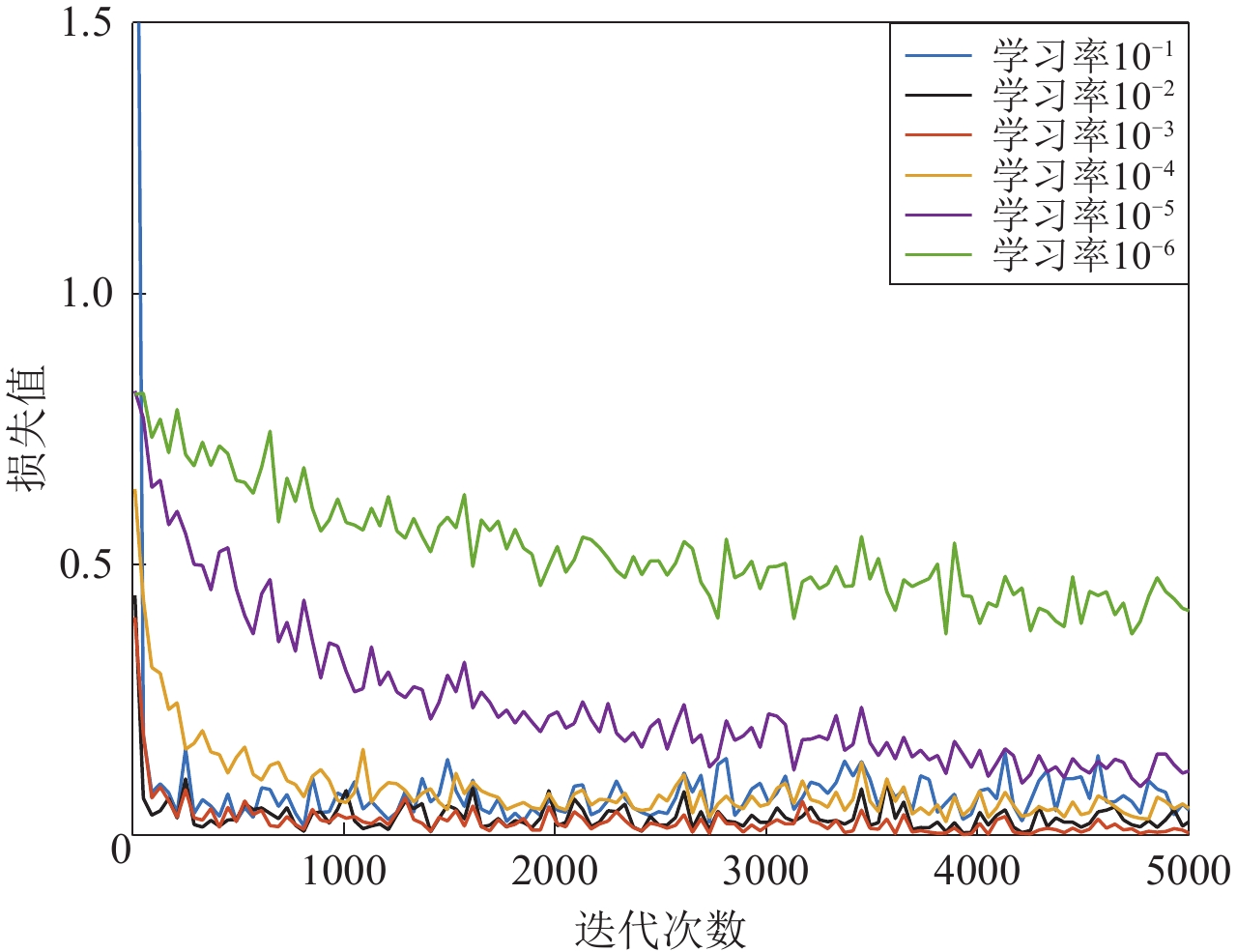
Ross等（2018b）在训练模型时，在10−4—10−1的范围内测试了多个学习率。在对测试数据集进行验证时，观察到当学习率为10−3时，模型很快达到收敛，损失值也更低。我们使用相同的数据集，采用不同的学习率进行训练，比较损失函数的变化。由图10可以看出，当学习率为10−5或10−6时，收敛的速度很慢；当取10−3时收敛快，而且损失值相比于其它学习率更低；学习率为10−1，10−2时，虽然收敛速度快但不够稳定，训练步数超过2 000时，仍然存在严重的震荡现象，而且损失值较10−3要高一些。
4.6 网络层数
卷积神经网络由多个卷积层和池化层交叉叠加组成，通过全连接层把提取的特征整合在一起，再通过Softmax函数分类输出。从输入到输出过程中，学习特征的“级别”可以通过加深层数来丰富（Mousavi et al，2019）。层数越多的网络，对数据的表达能力也越强，但并不是层数越多越好。如果训练数据不够多，很难训练一个深层网络。发生过拟合的一个可能原因就是使用了较深的网络层数。
Perol等（2018）和Zhou等（2019）通过测试和比较，使用了具有8个卷积层的神经网络。本文利用相同数据集、相同的网络结构，但不同的网络层数进行了比较（表3）。结果表明，采用不同的网络层数，检测结果相差不大，准确率、召回率、精确率和F1值的变化范围均小于2%。但使用较深的网络层数，会增加模型训练时间。从检测效果和训练时间综合考虑，对于地震检测，采用6—8层的神经网络都较为合适。
表 3 不同网络层数的检测结果对比Table 3. Comparison of detection results with different network layers层数 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 5 2 916 2 963 98.02% 97.23% 98.80% 98.01% 6 2 946 2 933 98.02% 98.23% 97.81% 98.02% 7 2 941 2 952 98.25% 98.07% 98.43% 98.25% 8 2 941 2 939 98.03% 98.07% 98.00% 98.03% 9 2 912 2 982 98.27% 97.10% 99.42% 98.25% 4.7 概率阈值
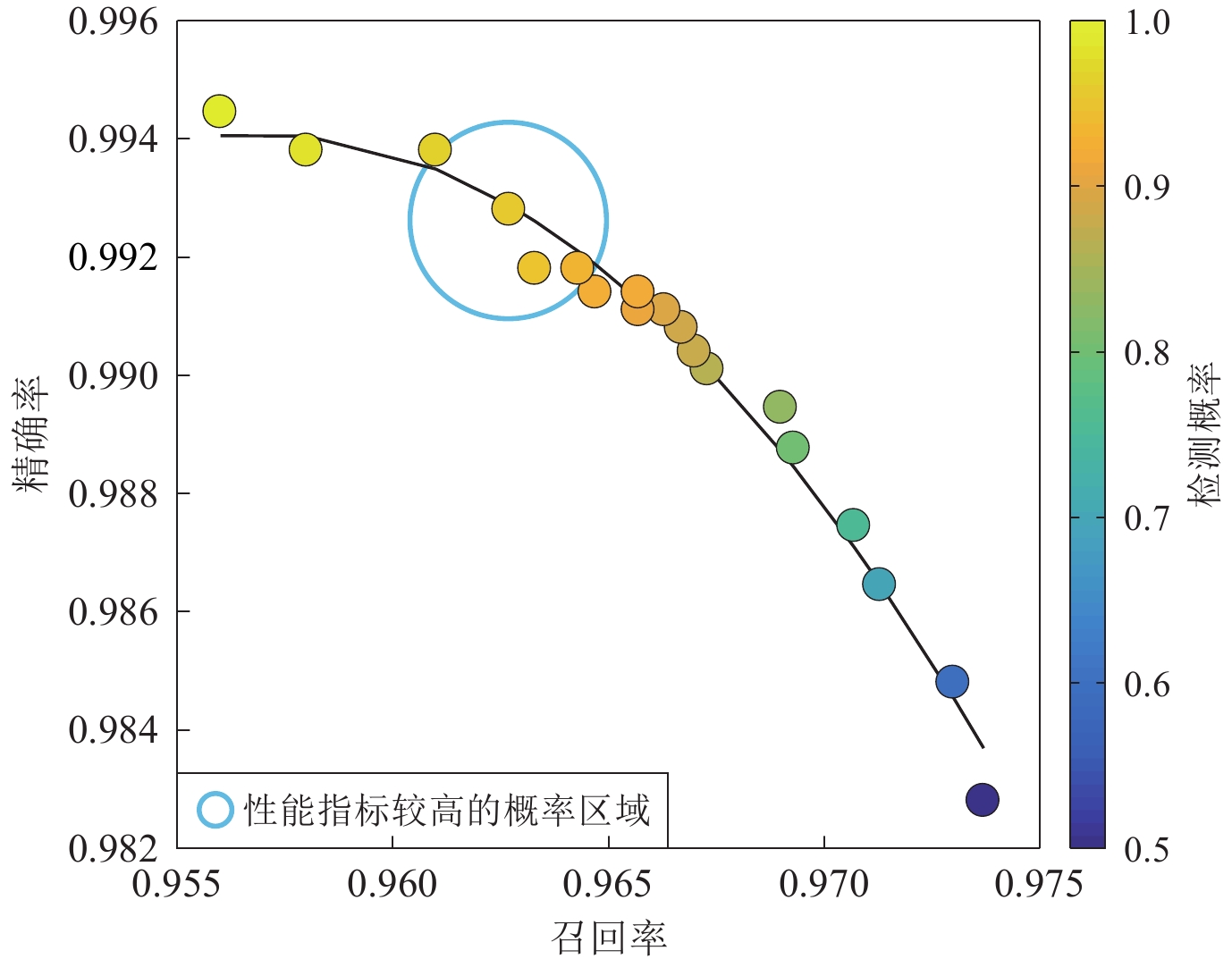
使用CNN训练好的模型检测地震数据时，模型会使用Softmax函数给出待检测波形是否为地震的概率，概率值分布范围为0—1。当设定的概率阈值较高时，检测出真实地震的可能性较高，但是可能会造成漏检。反之，漏检的可能性较低，但有可能检测出的大部分事件不是地震信号。因此，选择一个合理的概率阈值就显得尤为重要。如果一个模型的检测性能较好，它的召回率增长时，精确率也应该保持在一个较高的水平。图11是精确率-召回率变化曲线。可以看出，随着召回率的增加，精确率降低。浅蓝色圆圈表示性能指标较高的概率区域，其概率阈值约为90%，既能提高检测的准确率，也能降低识别的误报率。
![]()
图 11 不同概率阈值的精确率-召回率权衡曲线Figure 11. Precision-recall tradeoff curves fordifferent probability thresholds4.8 检测结果筛选
为检验模型的实际检测能力，我们使用训练好的最优模型检测了2018年4月份西昌台阵记录地震最多的5个台站的连续波形数据。将三分量连续波形截取为15 s窗口，滑动步长为1 s。在窗口滑动过程中，同一次地震有可能会被多次检测到。我们对2013—2017年西昌台阵记录的近震目录进行了分析，发现8 321次地震中，仅有3次相邻地震的发震时刻差异小于5 s。根据这一标准，我们对检测出来的地震到时进行了筛选，如果同一台站、同一震相类型前后相邻时间差小于5 s，则选取概率值高的为地震窗口。图12是筛选前后的震相数量对比。可以看出，通过发震时刻数据筛选，剔除了约60%的震相数据，为后续的震相关联和地震定位提供了更准确的输入数据。图13为训练得到的最优模型在连续波形中检测出来的波形。
![]()
图 12 筛选前后的地震数量统计Figure 12. Histogram of earthquakesdetected before and after screening![]()
图 13 CNN检测出的一个近震波形地震发震时刻为2018年4月28日23时2分43.8秒；震中位置为 （101.846°E，29.251°N）；震级为ML1.5. 图中仅显示了垂直分量；红线是人工拾取的P波到时；虚线框是检测到的地震窗口Figure 13. Waveforms of a local earthquake detected with CNNOccurrence time：23:02:43.8 on April 28，2018；epicenter location：101.846°E，29.251°N；ML1.5. Only vertical component is shown in the figure. The red line is the manually picked P wave arrivals. The dotted box is the detected earthquake window5. 讨论
利用深度学习检测地震是一个复杂的过程，包括构建网络模型、建立训练数据集、数据清洗预处理、网络参数调优，以及检测结果质量控制等关键步骤。地震波形数据的多样性和深层神经网络众多的超参数都会影响模型的泛化能力和检测精度。尽管国内外研究人员利用深度学习检测地震和拾取震相到时取得了很多进展，但关于数据处理和网络模型训练相关的细节却很少有研究人员给出详细的说明。
数据预处理对于深层卷积神经网络的训练非常重要。数据预处理过程直接影响神经网络的收敛，也会影响模型的预测结果（Haykin，2010）。在数据预处理阶段，主要步骤包括去均值、去倾斜、振幅归一化、滤波和数据清洗。受温度、压力和台基倾斜等影响，地震记录经常偏离零点。过大的零漂会使得激活函数饱和，同时压制有效信号（于子叶等，2018）。训练集中的地震震级和振幅变化范围较大，而绝对振幅并非地震检测中的有效特征，采用振幅归一化并不会降低有效特征，而且还可以压制震级和振幅随震中距衰减等因素的影响，加快梯度下降的求解速度。滤波可以有效地去除随机干扰，压制高频和低频噪声，模型训练时收敛更稳定，降低损失函数和准确率的震荡。Perol等（2018）对数据进行归一化处理，通过增加高斯噪声的事件窗口来增加训练集事件数量，平衡了训练集中的事件和噪声窗口的数量，防止模型过拟合。Ross等（2018a）选取P波和S波窗口以相应的到时为中心截取4 s的窗口，以每个P波到时之前5 s开始截取4 s的噪声窗口，对数据进行去倾斜、归一化和2 Hz高通滤波。Zhou等（2019）通过P和S的到时差选取P波到时之前0—15 s的随机数截取30 s的窗口，对数据作去均值、去倾斜、振幅归一化以及1 Hz的高通滤波。由图6a可见，原始训练数据如果不作预处理，在验证集或应用于连续波形检测时，效果会相对较差。
利用深度学习检测地震需要大量的训练样本。Ross等（2018a）和Zhu等（2018）都使用了百万量级左右的地震波形，在地震检测、到时拾取和模型泛化性方面都取得了较好的结果。但在实际训练时，可能会面临训练数据不足的问题，这时可以采用数据增强，包括加高斯噪声、平移、拉伸和随机裁剪等，来扩展训练数据集。由表1可以看出，数据增强后，准确率、召回率和F1值都有提升。目前，噪声数据集一般都选取地震前的一段窗口，这段窗口也有可能包含地震，尤其是对于地震序列而言，其发震间隔可能小于数秒。另外，如果震中距较远，由于地震波的衰减，地震特征可能也不明显。对于噪声数据中包含的地震和地震中包含的噪声，可以根据神经网络模型检测的结果，将分类错误的地震移到噪声集，反之亦然，这样可以进一步提高地震的检测精度。关于数据集中训练集和验证集的分配比例，训练集一般占70%—80%。Kriegerowski等（2018）使用的训练集与验证集的比例为7 ∶ 3，Ross等（2018b）训练集和验证集的比例为3 ∶ 1，Zhu等（2018）训练集、验证集和测试集的比例约为8 ∶ 1 ∶ 1。本文训练集约占数据集的81%。训练集中的地震波形数量和噪声波形数量最好相近（Hensman，Masko，2015）。
本文的研究表明，训练集的波形长度应该根据台网孔径、台站间距和地震分布选择合理的数值，应包含较为完整的地震波形，同时也不能引入P波前较长的噪声和S波后过长的尾波信号。Perol等（2018）的训练集震中距小于60 km，截取的地震波形窗口长度为10 s。Zhou等（2019）和Zhu等（2018）分别使用了汶川余震和北加州的地震数据训练模型，由于这两个地区台网覆盖面积较大，因此均使用了30 s的窗口长度。而Ross等（2018b）使用的南加州地震台网的数据，虽然台网孔径较大，却只用了4 s的窗口。虽然到时拾取精度较高，但是误拾取比率也较高。Zhu等（2018）训练卷积神经网络检测汶川余震时，也尝试了2.5，5，10，20，40 s的窗口长度，发现20 s窗口的检测准确率最高。赵明等（2019）利用U型神经网络检测汶川余震和首都圈地区的地震时，因Pg和Sg到时差最大不会超过25 s，因此统一裁切为30 s长度。由表1可以看出，选择合适的训练窗口，可将检测的准确率提高3%左右。关于检测窗口的长度，可以先分析训练集的S－P到时差分布，波形长度可近似于S－P到时差的最大值。以西昌台阵数据为例（图7），S－P到时差的最大值约为15 s，测试结果表明，当训练集的窗口长度设为15 s时综合性能较优（表2）。
本文还测试了网络层数、学习率和概率阈值对模型训练和检测结果的影响。采用不同的网络层数（5—8层），检测结果相差不大。但使用较深的网络架构，模型训练时间会急剧增加（Dokht等，2019）。当网络层数较多，而数据集较小时，容易出现过拟合现象。5—8层的网络深度都比较适于地震检测。学习率的选择应根据以下原则选取：在模型训练时，随着迭代次数的增加，损失函数缓慢下降，曲线相对平滑，最终收敛在损失函数很低的水平上。本文分别测试了10−6—10−1的多个学习率，当学习率设为10−3时，准确率、召回率、精确率综合检测结果最优。
6. 结论
本文以西昌台阵观测的近震数据为例，详细介绍了利用深度卷积神经网络检测地震的数据处理流程，包括地震数据预处理、模型训练、窗口长度、网络层数和学习率等关键参数对检测结果的影响，并将训练得到的最优模型，用于连续波形的检测。
研究表明，数据预处理（去均值、去倾斜、振幅归一化和滤波）、数据增强，可以提升模型的检测精度和抗干扰能力。当训练集较少时，可以采用加高斯噪声、拉伸、压缩和平移等数据增强方法扩展数据集。用于模型训练的波形长度，应尽可能包含完整的地震信息，但也不宜过长，可根据S－P到时差的优势分布设定，波形长度可近似于S－P到时差的最大值。训练集中P波到时在窗口中的位置对检测结果有重要影响，在构建训练集时，P波到时前的波形长度最好随机选取。5—8层的网络深度都比较适于地震检测，检测结果变化不大。但使用较深的网络层数，模型训练时间会较长。对于地震检测，学习率取10−4—10−3都是较为合理的选择区间。
与长短窗、模板匹配等地震检测方法类似，卷积神经网络检测出的地震数量也与选择的概率阈值有关。当概率阈值较高时，检测出真实地震的可能性较高，但可能会漏检。反之，有可能导致误检率较高。通过绘制精确率-召回率变化曲线，可以为选择合适的概率阈值提供参考。当卷积神经网络用于检测连续波形时，可根据检测概率、信噪比和长短窗比值同时判定，以进一步保证到时检测结果的可靠性，为震相关联和地震定位提供高质量的输入数据。
中国地震科学探测台阵数据中心整理了西昌台阵的波形数据；美国加州大学河滨分校周一剑博士、中国地震局地球物理研究所副研究员赵明和中国科学院地质与地球物理研究所肖卓伟博士在模型训练方面提供了帮助；两位审稿专家提供了意见和建议，尤其是有关训练窗口长度和数据增强的建议，使本文的分析讨论更加深入，作者在此一并表示衷心的感谢。
-
![]()
图 4 卷积、池化、全连接层局部示意图
Figure 4. Schematic diagram of convolution，pooling and fully connected layers
![]()
图 5 训练和验证曲线
Figure 5. The training accuracy，validation accuracy for events and noise and loss function curves
![]()
图 6 预处理前后的训练和验证曲线
Figure 6. Training and validation accuracy curves before and after data preprocess
![]()
图 8 不同窗长的训练步数与训练时间的关系
Figure 8. Relationship between training step and training time for different window lengths
![]()
图 9 P波到时前不同窗长的检测结果
（a） P波到时前窗长为4 s；（b） P波到时前窗长为0—7.5 s的随机值
Figure 9. Detection results of different window lengths before the P-wave arrival
（a） The window length before P-wave arrival is 4 s；（b） The window length beforeP-wave arrival is a random varying between 0 and 7.5 s
![]()
图 11 不同概率阈值的精确率-召回率权衡曲线
Figure 11. Precision-recall tradeoff curves fordifferent probability thresholds
![]()
图 12 筛选前后的地震数量统计
Figure 12. Histogram of earthquakesdetected before and after screening
![]()
图 13 CNN检测出的一个近震波形
地震发震时刻为2018年4月28日23时2分43.8秒；震中位置为 （101.846°E，29.251°N）；震级为ML1.5. 图中仅显示了垂直分量；红线是人工拾取的P波到时；虚线框是检测到的地震窗口
Figure 13. Waveforms of a local earthquake detected with CNN
Occurrence time：23:02:43.8 on April 28，2018；epicenter location：101.846°E，29.251°N；ML1.5. Only vertical component is shown in the figure. The red line is the manually picked P wave arrivals. The dotted box is the detected earthquake window
表 1 利用不同规模训练集训练得到的CNN模型检测结果对比
Table 1 Comparison of CNN model detection results from different training sets
编号 训练集
地震次数训练集地震
波形条数检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 1 1 334 6 595 2 882 2 937 97.02% 96.10% 97.89% 96.99% 2 1 334×3 19 785 2 924 2 936 97.70% 97.50% 97.89% 97.69% 3 1334×6 39 570 2 925 2 938 97.75% 97.53% 97.96% 97.75% 4 3 422 17 465 2 910 2 957 97.82% 97.03% 98.58% 97.79% 5 6 790 34 671 2 929 2 957 98.13% 97.67% 98.59% 98.13% 6 6 790×5 173 355 2 938 2 972 98.53% 97.97% 99.09% 98.53% 注：×号表示数据增强的倍数。测试集中的地震波形条数和噪声波形条数均为2 999条。 
下载: 导出CSV
表 2 采用不同窗长的训练集训练得到的CNN模型检测结果对比
Table 2 Comparison of CNN model detection results by training sets with different window lengths
窗口长度/s 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 10 2 904 2 950 97.60% 96.83% 98.34% 97.58% 15 2 929 2 957 98.13% 97.67% 98.57% 98.12% 20 2 920 2 944 97.77% 97.37% 98.15% 97.76% 25 2 904 2 948 97.57% 96.83% 98.27% 97.54% 30 2 900 2 944 97.43% 96.70% 98.14% 97.41% 35 2 895 2 959 97.60% 96.53% 98.64% 97.57% 40 2 904 2 954 97.67% 96.83% 98.47% 97.64%
下载: 导出CSV
表 3 不同网络层数的检测结果对比
Table 3 Comparison of detection results with different network layers
层数 检测出的地震
波形条数检测出的噪声
波形条数准确率 召回率 精确率 F1 5 2 916 2 963 98.02% 97.23% 98.80% 98.01% 6 2 946 2 933 98.02% 98.23% 97.81% 98.02% 7 2 941 2 952 98.25% 98.07% 98.43% 98.25% 8 2 941 2 939 98.03% 98.07% 98.00% 98.03% 9 2 912 2 982 98.27% 97.10% 99.42% 98.25%
下载: 导出CSV
-
蒋策,吴建平,房立华. 2018. 地震检测与震相自动拾取研究[J]. 地震学报,40(1):45–57. doi: 10.11939/jass.20170093 Jiang C,Wu J P,Fang L H. 2018. Earthquake detection and automatic phase picking[J]. Acta Seismologica Sinica,40(1):45–57 (in Chinese).
刘芳,蒋一然,宁杰远,张建中,赵艳红. 2020. 结合台阵策略的震相拾取深度学习方法[J]. 科学通报,65(11):1016–1026. Liu F,Jiang Y R,Ning J Y,Sun J Z,Zhao Y H. 2020. An array-assisted deep learning approach to seismic phase-picking[J]. Chinese Science Bulletin,65(11):1016–1026 (in Chinese).
李安. 2019. 基于深度学习的地震事件与震相自动识别[D]. 北京: 中国地震局地球物理研究所: 40–41. Li A. 2019. Automatic Recognition of Seismic Events and Phase Picking Based on Deep Learning[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 40–41 （in Chinese）.
杨旭,李永华,苏伟,孙莲. 2019. 基于优化参数的地震P、S波震相到时自动拾取及质量评估[J]. 地球物理学报,62(11):4290–4299. doi: 10.6038/cjg2019M0059 Yang X,Li Y H,Su W,Sun L. 2019. Optimized automatic pickers and quality assessment:Application to identification of local and regional P and S wave phases[J]. Chinese Journal of Geophysics,62(11):4290–4299 (in Chinese).
于子叶,储日升,盛敏汉. 2018. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报,61(12):151–164. Yu Z Y,Chu R S,Sheng M H. 2018. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics,61(12):4873–4886 (in Chinese).
赵明,陈石,房立华,David A Y. 2019. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报,62(8):3034–3042. Zhao M,Chen S,Fang L H,David A Y. 2019b. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. Chinese Journal of Geophysics,62(8):3034–3042 (in Chinese).
Allen R V. 1978. Automatic earthquake recognition and timing from single traces[J]. Bull Seismol Soc Am,68(5):1521–1532.
Baer M,Kradolfer U. 1987. An Automatic phase picker for local and teleseismic events[J]. Bull Seismol Soc Am,77(4):1437–1445.
Baillard C,Crawford W C,Ballu V,Hibert C,Mangeney A. 2014. An automatic kurtosis- based P- and S- phase picker designed for local seismic networks[J]. Bull Seismol Soc Am,104(1):394–409.
Dokht R M H,Kao H,Visser R,Smith B. 2019. Seismic event and phase detection using time–frequency representation and convolutional neural networks[J]. Seismol Res Lett,90(2A):481–490.
Earle P S,Shearer P M. 1994. Characterization of global seismograms using an automatic-picking algorithm[J]. Bull Seismol Soc Am,84(2):366–376.
Gibbons S J,Ringdal F. 2006. The detection of low magnitude seismic events using array-based waveform correlation[J]. Geophys J Int,165(1):149–166.
Haykin, Simon S. 2010. Neural Networks and Learning Machines[M]. Third Edition. Prentice Hall: Pearson Education India: 146–147.
Hensman P, Masko D. 2015. The Impact of Imbalanced Training Data for Convolutional Neural Networks[M]. Sweden: KTH Royal Institute of Technology: 1–28.
Kingma, Diederik P, Jimmy Ba. 2015. Adam: A method for stochastic optimization[EB/OL] [2020–12–17]. https://arxiv.org/abs/1412.6980.
Kriegerowski M,Petersen G M,Vasyura-Bathke H,Ohrnberger M. 2018. A deep convolutional neural network for localization of clustered earthquakes based on multistation full waveforms[J]. Seismol Res Lett,90(2A):510–516.
Krizhevsky A, Sutskever I, Hinton G E. 2012. Imagenet classification with deep convolutional neural networks[C]//Advances in Neural Information Processing Systems. Tahoe: NV: 1097–1105.
Mousavi S M,Zhu W Q,Sheng Y X,Beroza G C. 2019. CRED:A deep residual network of convolutional and recurrent units for earthquake signal detection[J]. Scientific Reports,9(1):1–14.
Nair V, Hinton G E. 2010. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the 27th International Conf. on Machine Learning ICML-10. Haifa: Israel: 807–814.
Ng A Y. 2004. Feature selection, L1 vs L2 regularization, and rotational invariance[C]//Proceedings of the Twenty-First International Conference on Machine Learning. Banff: 78.
Peng Z G,Zhao P. 2009. Migration of early aftershocks following the 2004 Parkfield earthquake[J]. Nat Geosci,2(12):877–881.
Powers,David M W. 2011. Evaluation:From precision,recall and F-measure to roc,informedness,markedness and correlation[J]. J Mach Learning Techn,2(1):37–63.
Perol T,Gharbi M,Denolle M. 2018. Convolutional neural network for earthquake detection and location[J]. Sci Adv,4(2):e1700578.
Ross Z E,Meier M A,Hauksson E,Heaton T H. 2018a. Generalized seismic phase detection with deep learning[J]. Bull Seismol Soc Am,108(5A):2894–2901.
Ross Z E,Meier M A,Hauksson E. 2018b. P wave arrival picking and first-motion polarity determination with deep learning[J]. J Geophys Res,123(6):5120–5129.
Saragiotis C D,Hadjileontiadis L J,Panas S M. 2002. PAI-S/K:A robust automatic seismic P phase arrival identification scheme[J]. IEEE T Geosci Remote,40(6):1395–1404.
Sleeman R,van Eck T V. 1999. Robust automatic P-phase picking:An on-line implementation in the analysis of broadband seismogram recordings[J]. Phys Earth Planet In,113(1-4):0–275.
Wang J,Xiao Z W,Liu C,Zhao D P,Yao Z X. 2019. Deep learning for picking seismic arrival times[J]. J Geophys Res,124(7):6612–6624.
Wilson D R,Martinez T R. 2003. The general inefficiency of batch training for gradient descent learning[J]. Neural Netw,16:1429–1451.
Yoon C E,O’Reilly O,Bergen K J. 2015. Earthquake detection through computationally efficient similarity search[J]. Sci Adv,1(11):e1501057.
Zhou Y J,Yue H,Kong Q K,Zhou S Y. 2019. Hybrid event detection and phase-picking algorithm using convolutional andrecurrent neural networks[J]. Seismol Res Lett,90(3):1079–1087.
Zhu W Q,Beroza G C. 2018. PhaseNet:A deep-neural-network-based seismic arrival-time picking method[J]. Geophys J Int,216(1):261–273.
-
期刊类型引用(10)
1. 李振，刘鹏飞，次仁多吉. 基于深度神经网络的地震预警数据实时高频云接收算法. 工程地球物理学报. 2024(06): 946-953 . 
百度学术
2. 周本伟，张丽芬，戴苗，赵凌云，魏贵春，周舟. PhaseNet与EQTransformer的震相拾取对比研究. 大地测量与地球动力学. 2023(06): 656-660 . 百度学术
3. 李昊，高林生，刘麟，邵坤. 深度学习在煤矿水力压裂微震检测中的应用. 西安科技大学学报. 2023(04): 686-696 . 百度学术
4. 许祥，邹志辉，韩明亮，贾冬顺，周华伟，裴建新，马锐. 联合地震初至走时与早至波形的深度学习速度建模. 地球物理学报. 2023(12): 5107-5122 . 百度学术
5. 于智瀚，王涛，孙鹏远，王文闯，郭振波. 基于小样本卷积神经网络的主动源P波初至拾取方法. 高校地质学报. 2022(03): 414-423 . 百度学术
6. 张珂，张帆，张晖，王鑫，郝美仙，翟浩. 内蒙古敖汉旗震群的微震匹配定位及其发震断层研究. 地震学报. 2022(04): 594-607 . 本站查看
7. 刘涛，戴志军，陈苏，傅磊. 基于深度学习的地震震级分类. 地震学报. 2022(04): 656-664 . 本站查看
8. 文玺翔，沈旭章，周启明. 基于机器学习和短周期密集台阵资料研究北流地震余震特征. 地球物理学报. 2022(09): 3297-3308 . 百度学术
9. 申中寅，吴庆举. 卷积神经网络在远-近地震震相拾取中的应用及模型解释. 地震学报. 2022(06): 961-979 . 本站查看
10. 廖诗荣，张红才，范莉苹，李珀任，黄玲珠，房立华，秦敏. 实时智能地震处理系统研发及其在2021年云南漾濞M_S6.4地震中的应用. 地球物理学报. 2021(10): 3632-3645 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 1534
- HTML全文浏览量: 796
- PDF下载量: 185
- 被引次数: 14
