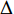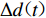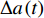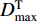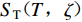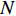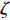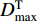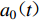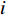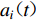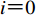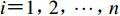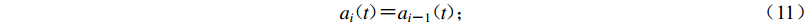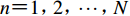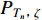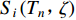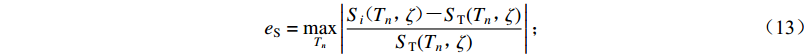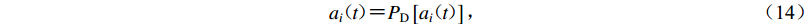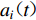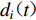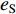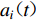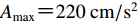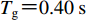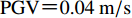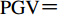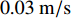A matching method of ground-motion response spectrum and the peak displacement based on the wavelet function
-
摘要: 采用数值方法合成地震动时，除对反应谱拟合外，对峰值位移的拟合和天然地震动非平稳特性的模拟也具有重要的意义和工程应用前景。本文基于小波函数的拟合方法，提出了一种能够同时合成目标反应谱和峰值位移的地震动加速度时程。数值算例表明：该方法具有较快的收敛速度，可用较少的迭代运算实现对目标反应谱和目标峰值位移的较高精度拟合；相较于现有的其它拟合方法，由于所构造的小波函数具有时域局部特点，该方法合成的地震动能够较好地保留天然地震动的非平稳特性。Abstract: When using numerical methods to synthesize ground motions, in addition to fitting the response spectrum, the fitting of peak displacements and the simulation of the non-stationary characteristics of natural ground motions also have important significance and engineering application prospects. Based on the wavelet function fitting method, this paper proposes a ground motion acceleration time history that can synthesize the target response spectrum and peak displacement at the same time. Numerical calculation examples show that this method has a faster rate of convergence, and can achieve a higher precision fitting of the target response spectrum and target peak displacement through less iterative calculations. Moreover, compared with other existing methods, the ground motion synthesized by this method can retain the non-stationary characteristics of natural ground motion, due to the local characteristics of wavelet function in time domain.
-
Keywords:
- ground motion /
- peak displacement /
- response spectrum /
- non-stationary characteristics /
- synthesize
-
引言
在重大工程的场地地震反应分析和结构抗震计算的时程分析中，人工合成地震动时程是普遍采用的确定动力系统输入的一种方式（胡灿阳，陈清军，2008；张翠然，陈厚群，2008）。该方法通过在频域或时域内调整初始地震动（又称“种子”地震动），使其反应谱逐步逼近目标反应谱（胡聿贤，何训，1986；蔡长青，沈建文，1997），该处理过程通常被称为地震动反应谱拟合。
地震动是一个复杂的时间过程，除反应谱参数外，地震动的位移特性以及非平稳特性对结构的地震反应，尤其是非线性反应都有明显的影响（周媛，2006；孙忠贤，2009；张郁山，赵凤新，2011；王飞，2016；郝明辉等，2017）。反应谱相近，峰值位移（张郁山，赵凤新，2011；郝明辉等，2017）或非平稳特性（柳夏勃，俞瑞芳，2016）差异较大的地震动引起的结构地震反应具有系统性的显著差异。很多规范均对地震动其它方面的特性进行了不同程度的概括。美国核安全标准审查大纲（U.S. Nuclear Regulatory Commission，2007，2014）关于核岛结构的设计明确要求地震动应具有与其所处地震环境相匹配的峰值速度（peak ground velocity，简写为PGV）和位移特性。为了使最终设计地震动具有天然地震动的非平稳特性，美国安全标准审查大纲（U.S. Nuclear Regulatory Commission，2007）规定，必须以实际强震动记录作为“种子”地震动；而且，如果作为非线性结构体系的输入，设计地震动的相位谱必须与“种子”地震动记录的相位谱保持一致（U.S. Nuclear Regulatory Commission，2014）。同样，我国 《城市轨道交通结构抗震设计规范》（中华人民共和国住房和城乡建设部，2014）对不同场地类别的设计地震动峰值位移的选取也作了相应的规定。因此，在拟合目标反应谱的同时，考虑对峰值位移的拟合以及对天然地震动非平稳特性的模拟，具有一定的理论意义与工程应用前景。
赵凤新和张郁山（2006，2007）利用在时域内叠加窄带时程的拟合方法，实现了同时对目标反应谱、目标峰值速度和目标峰值位移的拟合。由于窄带时程定义在整个时域内，该方法在保留天然地震动记录特性方面存在一定缺陷。盛涛等（2012）通过调整天然地震动记录的小波分量、并且在时域内叠加小波函数，实现了同时对目标反应谱、峰值位移（peak ground displacement，简写为PGD）和峰值加速度的拟合。该方法中，将对原始记录小波分量的调整作用在整个时间域，而叠加小波函数则将调整局限在某个局部时段。
当初始地震动选用天然强震记录时，采用窄带时程法会遇到拟合精度不够高或者收敛速度变慢的情况，因此，张郁山和赵凤新（2014）构造了拟合目标反应谱的小波函数，将对“种子”地震动的调整限制在局部，不仅实现了对目标谱的高精度拟合，而且较好地模拟了天然地震动的整体非平稳特性。本文拟在该方法的基础上，构造拟合峰值位移的小波函数，以期实现对目标反应谱和目标峰值位移的拟合，以及对天然地震动非平稳特性的模拟。
1. 构造增量小波函数
小波函数拟合方法是在初始地震动时程上叠加一系列时间函数（此处称为增量小波函数），使所得地震动的参数（如反应谱和峰值位移PGD）逐步逼近目标值。本文提出如下用于拟合目标PGD的增量加速度小波函数：
$$\Delta a{\text{（}}t{\text{）}}{\text{＝}}\frac{{\rm{d}}^{2}\left\{\psi {\text{（}}t{\text{－}}{t}_{\rm{D}}{\text{）}}\sin \left[2{\rm{\pi }}{f}_{{\rm{D}}{\text{，}}{\rm{p}}}{\text{（}}t{\text{－}}{t}_{\rm{D}}{\text{）}}\right]\right\}}{{\rm{d}}{t}^{2}}{\text{，}}$$ (1) 式中，fD， p为增量小波函数的频率，tD为小波函数的中心时刻，
$\psi {\text{（}}t{\text{）}}$ 为包络函数，其定义如下：$$\psi \left(t\right){\text{＝}}\left\{\begin{array}{c}\exp \left({\text{－}}\dfrac{{t}^{2}}{{c}_{1}}\right){\text{，}}\;\;\;\;t{\text{≤}} 0{\text{，}}\\ \exp \left({\text{－}}\dfrac{{t}^{2}}{{c}_{2}}\right){\text{，}}\;\;\;\;t{\text{＞}}0{\text{，}}\end{array}\right.$$ (2) 其中：
$$ {c}_{1}{\text{＝}}{\text{－}}\frac{{{\text{（}}{t}_{{\rm{D}}}{\text{－}}{t}_{1}{\text{）}}}^{2}}{\ln \varepsilon }{\text{，}}{c}_{2}{\text{＝}}{\text{－}}\frac{{{\text{（}}{t}_{2}{\text{－}}{t}_{{\rm{D}}}{\text{）}}}^{2}}{\ln \varepsilon }{\text{，}}$$ (3) t1和t2分别为增量小波函数有效区间的起止时刻，
$ \varepsilon $ 为控制参数，一般可取10−6。按照式（1）构造的增量加速度积分所得到的增量速度和增量位移均不存在基线漂移现象。因此，若初始地震动加速度时程不存在基线漂移，则利用式（1）对其调整后所得到的地震动也不会存在基线漂移问题（张郁山，赵凤新，2014）。在式（1）和（3）中，参数tD，fD， p，t1和t2由初始地震动位移时程确定。记初始地震动加速度为a0（t），起始时刻记为t0，终止时刻记为tE，则初始地震动位移
${d}_{0}{\text{（}}t{\text{）}}{\text{＝}}\iint {a}_{0}{\text{（}}t{\text{）}}{\rm{d}}t$ ，其绝对最大值Dmax出现时刻记为tD，即${D}_{\rm{max}}{\text{＝}}\left|{d}_{0}{\text{（}}{t}_{\rm{D}}{\text{）}}\right|$ ，该最大值所在位移脉冲的持时记为TD， d，定义为$$ {T}_{{\rm{D}}{\text{，}}{\rm{p}}}{\text{＝}}\min {\text{（}}{t}_{{\rm{D}}}{\text{－}}{{t}_{1}'}{\text{，}}{{t}_{2}'}{\text{－}}{t}_{{\rm{D}}}{\text{）}}{\text{，}}$$ (4) 其中：
$$\tag{5a} {{t}_{1}'}{\text{＝}}\left\{\begin{array}{l}{t}_{0}{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t}_{\rm{D}}-\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{＜}}{t}_{0}{\text{，}}\\ {t}_{\rm{D}}-\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{，}}\;\;\;{t}_{\rm{D}}-\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{≥}} {t}_{0}{\text{，}}\end{array}\right.$$ $$ \tag{5b} {{t}_{2}'}{\text{＝}}\left\{\begin{array}{l}{t}_{\rm{D}}{\text{＋}}\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{，}}\;\;\;{t}_{\rm{D}}{\text{＋}}\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{≤}} {t}_{\rm{E}}{\text{，}}\\ {t}_{\rm{E}}{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{t}_{\rm{D}}{\text{＋}}\dfrac{3}{2}{T}_{{\rm{D}}{\text{，}}{\rm{d}}}{\text{＞}}{t}_{\rm{E}}{\text{.}}\end{array}\right.$$ 利用该持时参数TD， p可定义所构造的增量小波函数的频率
$$ {f}_{{\rm{D}}{\text{，}}{\rm{p}}}{\text{＝}}\frac{3}{4{T}_{{\rm{D}}{\text{，}}{\rm{p}}}}$$ (6) 以及增量小波函数有效区间[t1，t2]的起止点
$$ {t}_{1}{\text{＝}}{t}_{\rm{D}}{\text{－}}{T}_{{\rm{D}}{\text{，}}{\rm{p}}}{\text{，}}{t}_{2}{\text{＝}}{t}_{\rm{D}}{\text{＋}}{T}_{{\rm{D}}{\text{，}}{\rm{p}}}{\text{.}}$$ (7) 记目标地震动的PGD为
$ {D}_{\rm{max}}^{\rm{T}} $ ，对式（1）定义的增量小波函数进行调整，并将其叠加在初始地震动加速度之上，即$$ {a}_{1}{\text{（}}{{t}}{\text{）}}{\text{＝}}{a}_{0}{\text{（}}{{t}}{\text{）}}{\text{＋}}{\rm{sgn}}\left[{d}_{0}{\text{（}}{t}_{\rm{D}}{\text{）}}\right]\frac{{D}_{\rm{max}}^{\rm{T}}{\text{－}}{D}_{\rm{max}}}{\Delta d{\text{（}}{{{t}}}_{\rm{D}}{\text{）}}}\Delta a{\text{（}}{{t}}{\text{）}}{\text{，}}$$ (8) 由a1（t）积分两次得到位移
${d}_{1}{\text{（}}t{\text{）}}{\text{＝}}\displaystyle\iint {a}_{1}{\text{（}}t{\text{）}}{\rm{d}}t$ ，则d1（t）的绝对最大值将等于目标值$ {D}_{\rm{max}}^{\rm{T}} $ 。式（8）中sgn（x）为符号函数，即$${\rm{sgn}}\left( x \right) {\text{＝}} \left\{ {\begin{array}{*{20}{l}} {1{\text{，}}\;\;\;\;\;\;\;\;\;\;{{x}} {\text{＞}} 0}{\text{，}}\\ {0{\text{，}}\;\;\;\;\;\;\;\;\;\;{{x}} {\text{＝}} 0}{\text{，}}\\ { {\text{－}} 1{\text{，}}\;\;\;\;\;\;{{x}} {\text{＜}} 0}{\text{.}} \end{array}} \right.$$ (9) 利用（8）式对初始地震动a0（t）进行的调整用算子PD简化表示，即
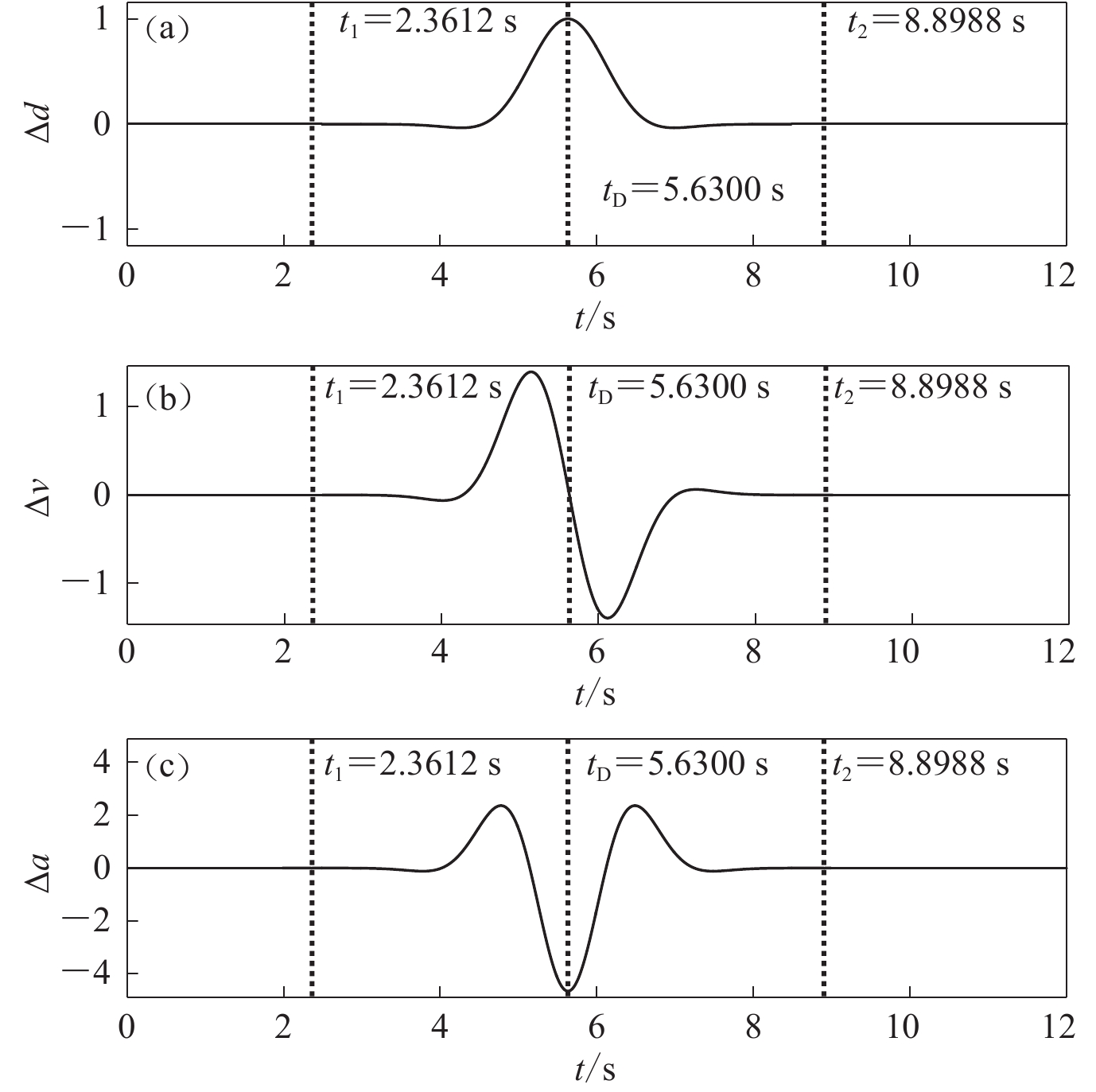
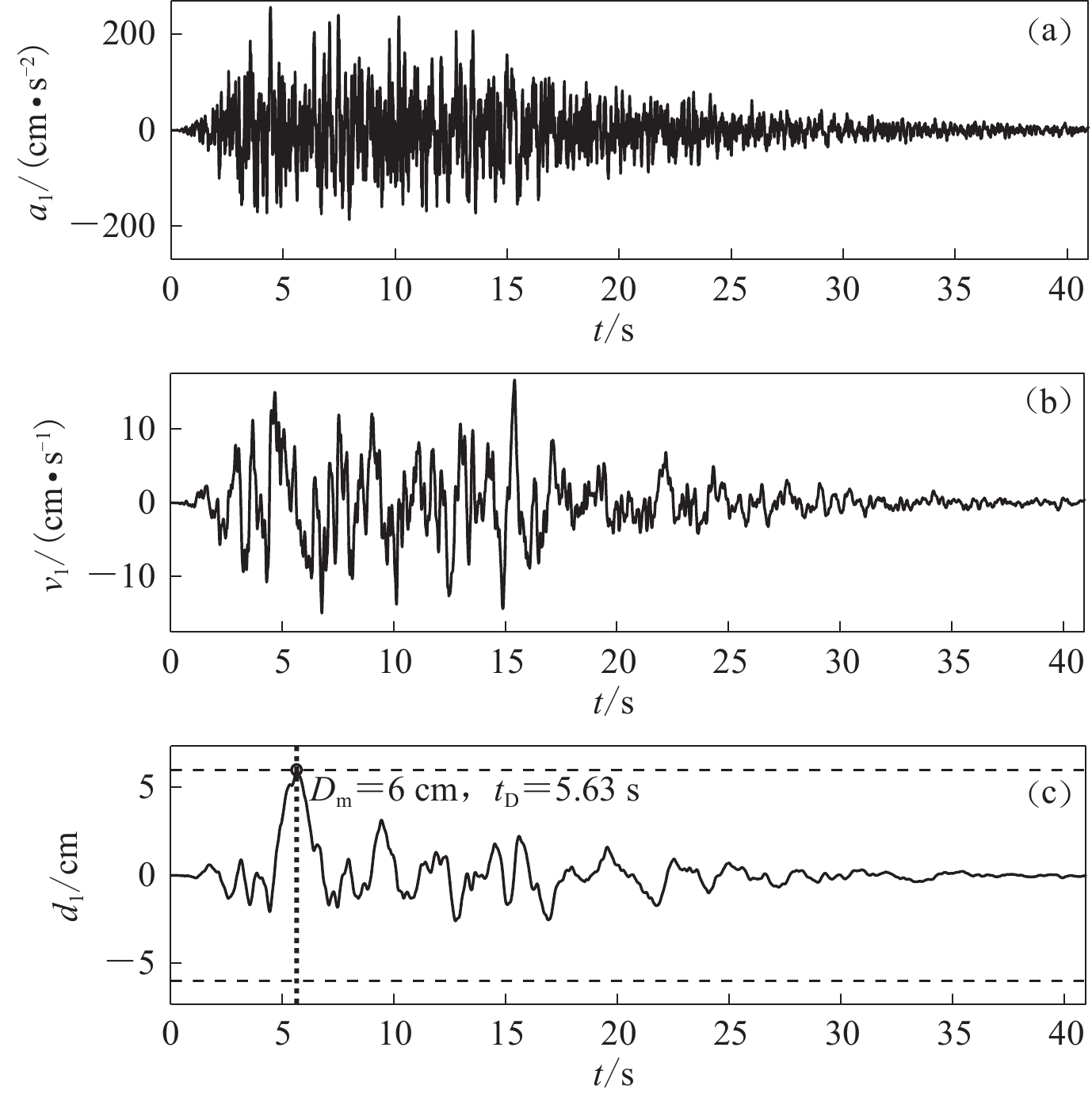
$${a}_{1}{\text{（}}{{t}}{\text{）}}{\text{＝}}{P}_{\rm{D}}\left[{a}_{0}{\text{（}}{{t}}{\text{）}}\right].$$ (10) 拟合目标峰值位移的过程如图1所示。对初始地震动加速度时程a0（t）（图1a）进行两次积分得到初始地震动位移时程d0（t） （图1c），图中目标峰值位移
${D}_{\rm{max}}^{\rm{T}}{\text{＝}} $ $ 6\;{\rm{cm}}$ ，峰值位移Dmax＝3.598 3 cm。![]()
图 1 初始地震动加速度（a）、速度（b）及位移（c）时程Figure 1. The initial ground-motion acceleration （a），velocity （b） and displacement （c） time histories初始地震动位移峰值Dmax附近的放大图形如图2所示，PGD所在位移脉冲及其持时TD， d也标在其中。图1中t0＝0 s，tE＝40.96 s，根据式（4），（6）和（7），可得TD， p＝3.268 8 s，fD， p＝0.2 Hz，t1 ＝ 2.361 2 s，t2＝8.898 8 s。将这些参数代入式（1），可得增量加速度小波函数
$ \Delta $ a（t）（图2c），其积分两次所得增量位移为$\Delta d{\text{（}}t{\text{）}}$ （图2a）。将$ \Delta a\left(t\right) $ 按式（8）调幅后，叠加在a0（t）上，得到a1（t）（图3a）；对a1（t）积分两次得到d1（t）（图3c）。可以看出，调整后地震动的位移峰值与目标值$ {D}_{\rm{max}}^{\rm{T}} $ 精确相等。![]()
图 2 用于调整初始地震动的增量小波函数（a） 增量位移时程；（b） 增量速度时程；（c） 增量加速度时程Figure 2. Incremental wavelet function for adjusting initial ground motion（a） Incremental displacement time history；（b） Incremental velocity time history；（c） Incremental acceleration time history![]()
图 3 调整后的初始地震动时程（a） 加速度时程；（b） 速度时程；（c） 位移时程.Dm 为调整后峰值位移，下同Figure 3. Adjusted initial ground-motion time history（a） Acceleration time history；（b） Velocity time history； （c） Displacement time history. Dm represents adjusted peak ground displacement，the same below分别对比初始地震动加速度时程和初始地震动位移时程（图4），可以看出，在一个局部时段内对初始地震动加速度进行调整可满足对目标PGD的拟合，并且调整后的加速度时程曲线保留了初始地震动的基本非平稳特征。
![]()
图 4 初始地震动加速度（a）、位移（b）时程与调整后比较Figure 4. Comparison of the initial ground-motion acceleration （a），displacement （b） time histories with the modified ones2. 拟合方法
本文采用张郁山和赵凤新（2014）提出的方法进行地震动反应谱拟合，即采用式（10）定义PGD调整算子进行地震动PGD的拟合，从而合成同时拟合反应谱和PGD的地震动。在地震动反应谱的拟合过程中，相邻周期之间存在耦合效应，而且对目标PGD的拟合也会对目标反应谱的拟合精度产生影响，这些影响效应可以通过迭代运算予以减轻（张郁山，赵凤新，2014）。
给定目标地震动反应谱
${S}_{\rm{T}}{\text{（}}{{T}}{\text{，}}{\rm{\zeta }}{\text{）}}$ ，其中Tn为离散周期点，$n={1{\text{，}}2}{\text{，}}\cdots{\text{，}}N$ （$ N $ 为目标反应谱控制周期点总数，$\zeta $ 为阻尼比；给定目标地震动PGD为$ {D}_{\rm{max}}^{\rm{T}} $ 。初始地震动加速度时程为${a}_{0}{\text{（}}t{\text{）}}$ ，它既可以采用随机过程理论方法生成，又可从强震动观测数据库中选用。本文提出的可同时对反应谱和PGD进行拟合的小波函数方法可归纳如下：1） 第
$ i $ 次迭代调整后，得到的加速度记为${a}_{i}{\text{（}}t{\text{）}}$ ，其中$i{\text{＝}}0$ 即对应初始加速度。2） 针对第i次迭代（
$i{\text{＝}}1{\text{，}}2{\text{，}}\cdots{\text{，}}n$ ），进行三步运算：① 令$$ {a}_{i}{\text{（}}t{\text{）}}{\text{＝}}{a}_{i{\text{－}}1}{\text{（}}t{\text{）}}{\text{；}}$$ (11) ② 针对
$ {T}_{n} $ （$n{\text{＝}}{1{\text{，}}2}{\text{，}}\cdots{\text{，}}N$ ），令$$ {a}_{i}{\text{（}}t{\text{）}}{\text{＝}}{P}_{{T}_{n}{\text{，}}\zeta }\left[{a}_{i{\text{－}}1}{\text{（}}t{\text{）}}\right]{\text{，}}$$ (12) 式中，反应谱调整算子
${P}_{{T}_{n}{\text{，}}\zeta }$ 的定义参见张郁山和赵凤新（2014）。按照上式，所有周期均调整之后，计算所得时程的反应谱${S}_{i}\left({T}_{n}{\text{，}}\zeta \right)$ 及其与目标谱之间相对误差的最大值$${e}_{\rm{S}}=\underset{{T}_{n}}{\rm{max}}\left|\frac{{S}_{i}{\text{（}}{T}_{n}{\text{，}}\zeta {\text{）}}{\text{－}}{S}_{\rm{T}}({T}_{n}{\text{，}}\zeta)}{{S}_{\rm{T}}({T}_{n}{\text{，}}\zeta)}\right|{\text{；}}$$ (13) ③ 按下式调整步骤②所得加速度
$$ {a}_{i}{\text{（}}t{\text{）}}{\text{＝}}{P}_{\rm{D}}\left[{a}_{i}{\text{（}}t{\text{）}}\right]{\text{，}}$$ (14) 使其拟合目标PGD。对所得
${a}_{i}{\text{（}}t{\text{）}}$ 通过两次积分得到位移${d}_{i}{\text{（}}t{\text{）}}$ ，计算其峰值与目标值之间的相对误差$$ {e}_{\rm{D}}{\text{＝}}\left|\frac{\underset{t}{\rm{max}}\left|{d}_{i}{\text{（}}t{\text{）}}\right|{\text{－}}{D}_{\rm{max}}^{\rm{T}}}{{D}_{\rm{max}}^{\rm{T}}}\right|{\text{.}}$$ (15) 3） 如果相对误差
${{e}}_{\rm{S}}$ 和${{e}}_{\rm{D}}$ 满足精度要求，即小于预先设定的精度控制参数（通常取5%），则所得${a}_{i}{\text{（}}{{t}}{\text{）}}$ 即为最终地震动加速度时程；若不满足精度要求，令$i{\text{＝}}i{\text{＋}}1$ ，重复步骤②进行调整，直到满足精度要求为止。3. 数值算例
基于上述研究，本文提出的拟合方法是以给定的精度要求，基于小波函数实现同时拟合目标反应谱和目标峰值位移的地震动合成方法。以我国《建筑抗震设计规范》（中华人民共和国住房和城乡建设部，2010）为依据，选择两条天然地震动作为初始地震动时程。关于天然强震记录的选取，许多研究者开展了相关工作，并提出了选取准则或选取条件（李琳等，2013；冀昆等，2016）。参考现有研究，本文以与目标谱之间相对误差最小的原则（U.S. Nuclear Regulatory Commission，2014），综合考虑地震震级和场地条件等因素（U.S. Nuclear Regulatory Commission，2007；王珊，张郁山，2017）对记录进行选取，所选记录的基本信息如表1所示。目标反应谱是根据规范给定的地震影响系数曲线的标准形式给出，其设计地震动反应谱曲线如图7a中黑色实线所示。其中，设计地震动峰值加速度
${A}_{\rm{max}}{\text{＝}}220\;{\rm{cm}}/{\rm{s}}^{2}$ ，特征周期${T}_{\rm{g}}{\text{＝}}0.40\;{\rm{s}}$ ，阻尼比为0.05 （王珊，张郁山，2017）。表 1 本文所用强震观测记录的基本信息Table 1. Fundamental information on the strong-motion observation recordings used in this paper发震日期 地震名称 台站名称 MW 震中距/km 分量 1999-08-17 土耳其地震 Maslak 7.5 90.74 EW 1999-09-20 中国台湾集集地震 CHY088 6.2 48.87 EW 以Maslak台站记录到的1999年8月17日土耳其MW7.5地震作为初始地震动时程（图5）。利用小波函数法合成“种子”地震动、目标反应谱和目标峰值速度相同，得到的两组地震动时程的目标峰值位移相差1倍，列于表2。固定目标峰值速度
${\rm{P}}{\rm{G}}{\rm{V}}{\text{＝}}0.04\;{\rm{m}}/{\rm{s}}$ ，目标峰值位移PGD分别取0.06 m和0.03 m，其时程曲线如图6所示。![]()
图 5 Maslak台站记录土耳其MW7.5地震的地震动加速度（a）、速度（b）和位移（c）时程Figure 5. The ground-motion acceleration （a），velocity （b） and displacement （c） time histories of the MW7.5 earthquake in Turkey recorded by the station Maslak表 2 以Maslak台站记录作为初始地震动的待拟合的目标参数Table 2. The target parameters to be matched with the records of the station Maslak as the initial ground-motion分组 PGA/g PGV/（m·s−1） PGD/m 第一组 0.22 0.04 0.06 第二组 0.22 0.04 0.03 ![]()
图 6 Maslak台站第一组（a）和第二组（b）设计地震动的加速度、速度和位移时程Figure 6. Group 1 （a） and group 2 （b） design ground motion acceleration，velocity and displacement time histories curves of the station Maslak从图6中可以看出，在张郁山和赵凤新（2014）提出的小波函数方法的基础上，得到的地震动整体特征变化不大，两组设计地震动的PGA和PGV基本相同，而第一组PGD是第二组的2倍。
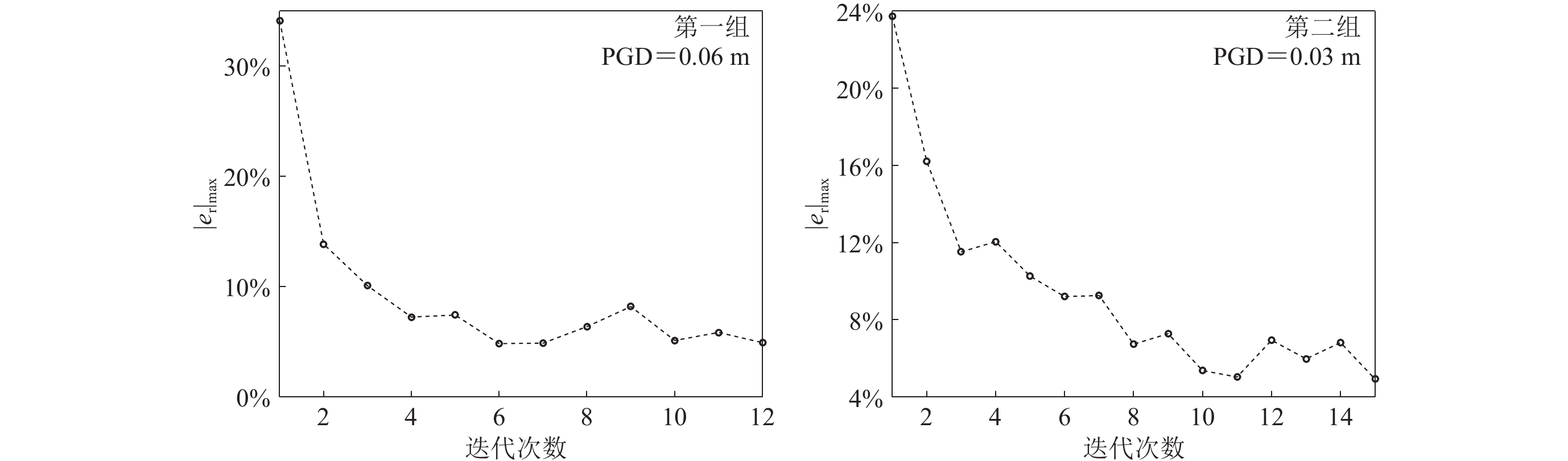
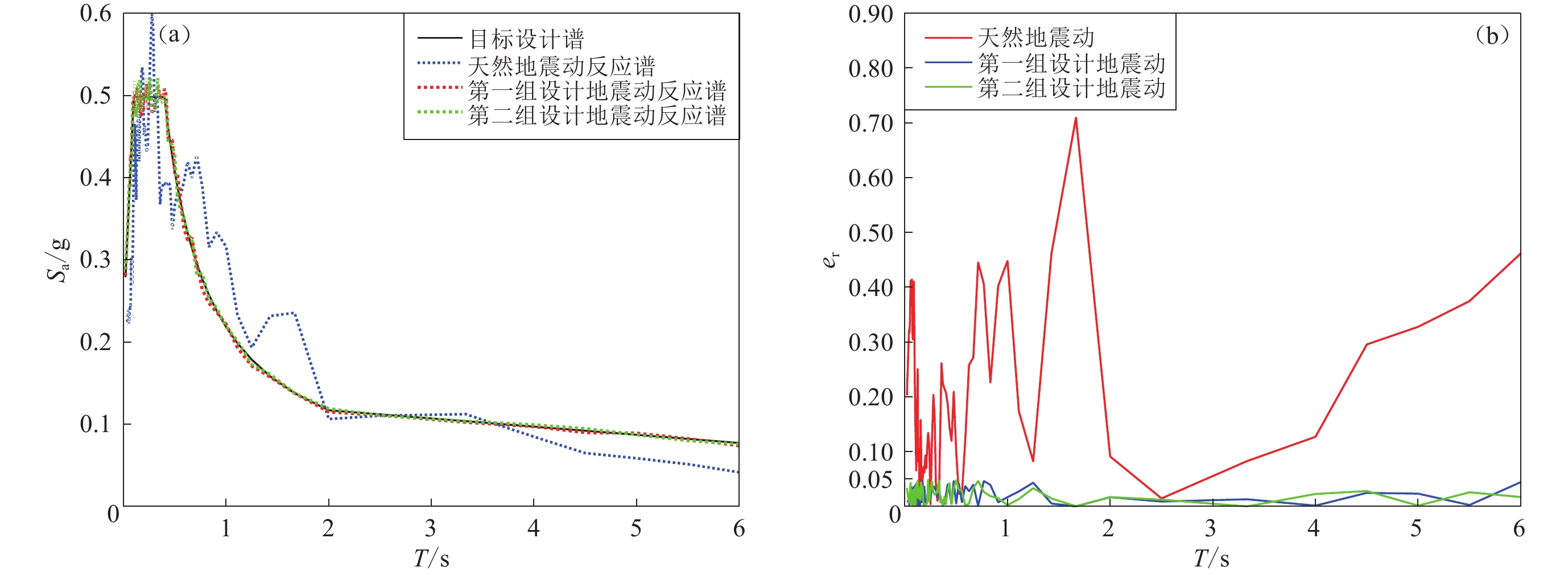
图6中设计地震动反应谱对目标谱的拟合情况如图7所示，将天然地震动反应谱、两组设计地震动反应谱与目标谱（图7a），以及第一组和第二组设计地震动反应谱与目标谱的相对误差（图7b）进行对比。可以看出，其相对误差的最大绝对值均低于5%。由图8所示的两组设计地震动反应谱与目标谱的相对误差与迭代调整次数的关系可见，第一组算例需12次迭代才能满足精度要求，第二组算例需15次迭代才能满足精度要求。
![]()
图 7 设计地震动加速度反应谱与目标谱的比较（a） 加速度反应谱Sa；（b） Maslak台站记录的相对误差erFigure 7. Comparison of target spectrum and design ground motion acceleration spectra（a） Acceleration spectrum Sa；（b） Relative errorer er of the records by the station Maslak![]()
图 8 Maslak台站记录拟合精度与迭代次数的变化关系Figure 8. Relationship between matching precision and iteration number of the records by the station Maslak以CHY088台站记录到的中国台湾集集MW6.2地震作为初始地震动时程，如图9所示。利用小波函数法合成“种子”地震动、目标反应谱和目标峰值速度相同，得到的两组地震动时程的目标峰值位移相差1倍（表3）。固定目标峰值速度
${\rm{P}}{\rm{G}}{\rm{V}}{\text{＝}} $ $ 0.03\;{\rm{m}}/{\rm{s}}$ ，目标峰值位移PGD分别取0.03 m和0.015 m，其时程曲线如图10所示。![]()
图 9 CHY088台站记录到的集集MW6.2地震的地震动加速度（a）、速度（b）和位移（c）时程曲线Figure 9. The ground-motion acceleration （a），velocity （b） and displacement （c） time histories of the MW6.2 Jiji earthquake recorded by the station CHY088表 3 以CHY088台站记录作为初始地震动时程待拟合的目标参数Table 3. The target parameters to be matched with the records of the station CHY088 as the initial ground-motion分组 PGA/g PGV/（m·s−1） PGD/m 第一组 0.22 0.03 0.03 第二组 0.22 0.03 0.015 ![]()
图 10 CHY088台站第一组（a）和第二组（b）的设计地震动加速度、速度和位移时程Figure 10. Group 1 （a） and group 2 （b） design ground motion acceleration，velocity，and displacement time histories curves of the station CHY088从图10可以看出，利用小波函数法得到的地震动整体上较好地保留了天然地震动的特性，两组设计地震动的PGA和PGV基本相同，而第一组PGD是第二组的两倍。
图10中设计地震动反应谱对目标谱的拟合情况如图11所示，将天然地震动反应谱、两组设计地震动反应谱与目标谱（图11a），以及第一组和第二组设计地震动反应谱与目标谱的相对误差（图11b）进行对比，可以看出，其相对误差的最大绝对值均低于5%。两组设计地震动反应谱与目标谱的相对误差与迭代调整次数的关系（图12）可见，第一组算例需11次迭代才能满足精度要求，第二组算例仅需6次迭代即可满足精度要求。由上可知，根据本文的方法得到的设计地震动时程既可以满足对目标反应谱的拟合精度要求，又可使峰值位移逼近目标值，并且可以较好地保留天然地震动的工程特性，具有较快的收敛速度，还不会出现基线漂移现象。
![]()
图 11 设计地震动加速度反应谱与目标谱的比较（a） 加速度反应谱Sa；（b） CHY088台站记录的相对误差 erFigure 11. Comparison of target spectrum and design ground motion acceleration spectra（a） Acceleration spectrum Sa；（b） Relative errorer er of the records by the station CHY088![]()
图 12 CHY088台站记录的拟合精度与迭代次数的变化关系Figure 12. Relationship between matching precision and iteration numbers of the records by the station CHY0884. 讨论与结论
在合成用于场地和结构地震反应计算的输入地震动时，除拟合目标反应谱外，考虑对目标地震动峰值位移的拟合以及对地震动非平稳特性的模拟具有理论与工程意义。本文构造了拟合峰值位移的小波函数，并以此为基础，提出了同时拟合目标地震动反应谱和峰值位移的方法。该方法不仅可以实现以较高精度对目标参数拟合，而且由于该方法具有较快的收敛速度和小波函数的局域特征，其所合成地震动能够较好地保留天然地震动的非平稳特性。该方法在重大工程场地地震动参数确定工作以及结构（尤其是中长周期结构）地震反应分析工作中具有较广工程应用前景。
本文考虑的是以单阻尼目标反应谱进行拟合，但在实际的工程中，需要合成多阻尼目标反应谱的情况比较多。如果对多阻尼目标反应谱进行拟合，给定的阻尼比个数越多，拟合难度越大，关于迭代的收敛速度以及算法的优化，是下一步需要考虑的问题。
-
![]()
图 1 初始地震动加速度（a）、速度（b）及位移（c）时程
Figure 1. The initial ground-motion acceleration （a），velocity （b） and displacement （c） time histories
![]()
图 2 用于调整初始地震动的增量小波函数
（a） 增量位移时程；（b） 增量速度时程；（c） 增量加速度时程
Figure 2. Incremental wavelet function for adjusting initial ground motion
（a） Incremental displacement time history；（b） Incremental velocity time history；（c） Incremental acceleration time history
![]()
图 3 调整后的初始地震动时程
（a） 加速度时程；（b） 速度时程；（c） 位移时程.Dm 为调整后峰值位移，下同
Figure 3. Adjusted initial ground-motion time history
（a） Acceleration time history；（b） Velocity time history； （c） Displacement time history. Dm represents adjusted peak ground displacement，the same below
![]()
图 4 初始地震动加速度（a）、位移（b）时程与调整后比较
Figure 4. Comparison of the initial ground-motion acceleration （a），displacement （b） time histories with the modified ones
![]()
图 5 Maslak台站记录土耳其MW7.5地震的地震动加速度（a）、速度（b）和位移（c）时程
Figure 5. The ground-motion acceleration （a），velocity （b） and displacement （c） time histories of the MW7.5 earthquake in Turkey recorded by the station Maslak
![]()
图 6 Maslak台站第一组（a）和第二组（b）设计地震动的加速度、速度和位移时程
Figure 6. Group 1 （a） and group 2 （b） design ground motion acceleration，velocity and displacement time histories curves of the station Maslak
![]()
图 7 设计地震动加速度反应谱与目标谱的比较
（a） 加速度反应谱Sa；（b） Maslak台站记录的相对误差er
Figure 7. Comparison of target spectrum and design ground motion acceleration spectra
（a） Acceleration spectrum Sa；（b） Relative errorer er of the records by the station Maslak
![]()
图 8 Maslak台站记录拟合精度与迭代次数的变化关系
Figure 8. Relationship between matching precision and iteration number of the records by the station Maslak
![]()
图 9 CHY088台站记录到的集集MW6.2地震的地震动加速度（a）、速度（b）和位移（c）时程曲线
Figure 9. The ground-motion acceleration （a），velocity （b） and displacement （c） time histories of the MW6.2 Jiji earthquake recorded by the station CHY088
![]()
图 10 CHY088台站第一组（a）和第二组（b）的设计地震动加速度、速度和位移时程
Figure 10. Group 1 （a） and group 2 （b） design ground motion acceleration，velocity，and displacement time histories curves of the station CHY088
![]()
图 11 设计地震动加速度反应谱与目标谱的比较
（a） 加速度反应谱Sa；（b） CHY088台站记录的相对误差 er
Figure 11. Comparison of target spectrum and design ground motion acceleration spectra
（a） Acceleration spectrum Sa；（b） Relative errorer er of the records by the station CHY088
![]()
图 12 CHY088台站记录的拟合精度与迭代次数的变化关系
Figure 12. Relationship between matching precision and iteration numbers of the records by the station CHY088
表 1 本文所用强震观测记录的基本信息
Table 1 Fundamental information on the strong-motion observation recordings used in this paper
发震日期 地震名称 台站名称 MW 震中距/km 分量 1999-08-17 土耳其地震 Maslak 7.5 90.74 EW 1999-09-20 中国台湾集集地震 CHY088 6.2 48.87 EW 
下载: 导出CSV
表 2 以Maslak台站记录作为初始地震动的待拟合的目标参数
Table 2 The target parameters to be matched with the records of the station Maslak as the initial ground-motion
分组 PGA/g PGV/（m·s−1） PGD/m 第一组 0.22 0.04 0.06 第二组 0.22 0.04 0.03
下载: 导出CSV
表 3 以CHY088台站记录作为初始地震动时程待拟合的目标参数
Table 3 The target parameters to be matched with the records of the station CHY088 as the initial ground-motion
分组 PGA/g PGV/（m·s−1） PGD/m 第一组 0.22 0.03 0.03 第二组 0.22 0.03 0.015
下载: 导出CSV
-
蔡长青,沈建文. 1997. 人造地震动的时域叠加法和反应谱整体逼近技术[J]. 地震学报,19(1):71–78. Cai C Q,Shen J W. 1997. Time-domain superposition method and response spectrum overall approximation technology of artificial ground motion[J]. Acta Seismologica Sinica,19(1):71–78 (in Chinese).
郝明辉,王珊,张郁山. 2017. 峰值位移输入对单自由度体系地震反应的影响[J]. 建筑结构学报,38(1):85–92. Hao M H,Wang S,Zhang Y S. 2017. Influence of input ground-motion peak displacement on non-linear dynamic response of single-degree-of-freedom system[J]. Journal of Building Structures,38(1):85–92 (in Chinese).
胡灿阳,陈清军. 2008. 非平稳地震地面运动分析方法及模型综述[J]. 结构工程师,24(2):107–115. doi: 10.3969/j.issn.1005-0159.2008.02.022 Hu C Y,Chen Q J. 2008. State-of-the-art of analysis method and model of non-stationary earthquake ground motion[J]. Structural Engineers,24(2):107–115 (in Chinese).
胡聿贤,何训. 1986. 考虑相位谱的人造地震动反应谱拟合[J]. 地震工程与工程振动,6(2):37–51. Hu Y X,He X. 1986. Phase angle consideration in generating response spectrum- compatible ground motion[J]. Earthquake Engineering and Engineering Vibration,6(2):37–51 (in Chinese).
冀昆,温瑞智,任叶飞. 2016. 中国抗震规范强震记录选取的初选条件研究[J]. 防灾减灾工程学报,36(1):44–49. Ji K,Wen R Z,Ren Y F. 2016. Study on the initial of selection criteria strong motion records for Chinese Seismic Code[J]. Journal of Disaster Prevention and Mitigation Engineering,36(1):44–49 (in Chinese).
李琳,温瑞智,周宝峰,史大成. 2013. 基于条件均值反应谱的特大地震强震记录的选取及调整方法[J]. 地震学报,35(3):380–389. doi: 10.3969/j.issn.0253-3782.2013.03.009 Li L,Wen R Z,Zhou B F,Shi D C. 2013. Selection and scaling of ground motion records for great scenario earthquake based on the conditional mean spectrum[J]. Acta Seismologica Sinica,35(3):380–389 (in Chinese).
柳夏勃,俞瑞芳. 2016. 地震动强度非平稳特性参数与结构响应之间的近似定量关系分析[J]. 地震学报,38(6):924–933. doi: 10.11939/jass.2016.06.012 Liu X B,Yu R F. 2016. Approximate quantitative relationship between earthquake ground motion and structural responses[J]. Acta Seismologica Sinica,38(6):924–933 (in Chinese).
盛涛,施卫星,谢异同,袁俊. 2012. 拟合核电厂设计反应谱及峰值位移的地震动调整方法[J]. 核动力工程,33(1):4–8. doi: 10.3969/j.issn.0258-0926.2012.01.002 Sheng T,Shi W X,Xie Y T,Yuan J. 2012. A modifying method of recorded earthquake ground motion for matching design response spectrum and peak ground displacement in nuclear power plants[J]. Nuclear Power Engineering,33(1):4–8 (in Chinese).
孙忠贤. 2009. 地震动特性对结构地震反应的影响分析[D]. 哈尔滨: 中国地震局工程力学研究所: 1–63. Sun Z X. 2009. The Influence of Ground Motion Characteristics on Response of Structures[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 1–63 （in Chinese）.
王飞. 2016. 峰值速度和峰值位移对钢结构弹塑性地震反应影响研究[D]. 北京: 中国地震局地球物理研究所: 1–406. Wang F. 2016. Influence of PGV and PGD on Structural Nolinear Seismic Response of Steel Buildings[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 1–406 （in Chinese）.
王珊,张郁山. 2017. 各类抗震设计规范对设计地震动时程规定的对比分析[J]. 中国地震,33(1):56–67. doi: 10.3969/j.issn.1001-4683.2017.01.006 Wang S,Zhang Y S. 2017. Comparison of various seismic design codes on design ground motion time history[J]. Earthquake Research in China,33(1):56–67 (in Chinese).
张翠然,陈厚群. 2008. 工程地震动模拟研究综述[J]. 世界地震工程,24(2):150–157. Zhang C R,Chen H Q. 2008. Review and prospects on the simulation research of engineering earthquake ground motion[J]. World Earthquake Engineering,24(2):150–157 (in Chinese).
张郁山,赵凤新. 2011. 地震动峰值位移对单自由度体系非线性动力反应的影响[J]. 工程力学,28(1):55–64. Zhang Y S,Zhao F X. 2011. Influence of ground-motion peak displacement on non-linear dynamic response of single-degree-of-freedom system[J]. Engineering Mechanics,28(1):55–64 (in Chinese).
张郁山,赵凤新. 2014. 基于小波函数的地震动反应谱拟合方法[J]. 土木工程学报,47(1):70–81. Zhang Y S,Zhao F X. 2014. Matching method of ground-motion response spectrum based on the wavelet function[J]. China Civil Engineering Journal,47(1):70–81 (in Chinese).
赵凤新,张郁山. 2006. 拟合峰值速度与目标反应谱的人造地震动[J]. 地震学报,28(4):429–437. doi: 10.3321/j.issn:0253-3782.2006.04.010 Zhao F X,Zhang Y S. 2006. Artificial ground motion compatible with specified peak velocity and target spectrum[J]. Acta Seismologica Sinica,28(4):429–437 (in Chinese).
赵凤新,张郁山. 2007. 拟合峰值位移与目标反应谱的人造地震动[J]. 核动力工程,28(2):38–41. doi: 10.3969/j.issn.0258-0926.2007.02.009 Zhao F X,Zhang Y S. 2007. Artificial ground motions compatible with both specified peak displacement and target response spectrum[J]. Nuclear Power Engineering,28(2):38–41 (in Chinese).
中华人民共和国住房和城乡建设部. 2010. GB 50011—2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社: 1–34. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. 2010. GB 50011—2010 Code for Seismic Design of Buildings[S]. Beijing: China Architecture & Building Press: 1–34 （in Chinese）.
中华人民共和国住房和城乡建设部. 2014. GB 50909—2014 城市轨道交通结构抗震设计规范[S]. 北京: 中国计划出版社: 1–26. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. 2014. GB 50909—2014 Code for Seismic Design of Urban Rail Transit Structures[S]. Beijing: China Planning Press: 1–26 （in Chinese）.
周媛. 2006. 地震动速度与位移对大跨斜拉桥地震反应影响的研究[D]. 北京: 中国地震局地球物理研究所: 1–88. Zhou Y. 2006. Study on Effects of Ground Velocity and Ground Displacement on Seismic Responses of Long Span Cable-Stayed Bridge[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 1–88 （in Chinese）.
U.S. Nuclear Regulatory Commission. 2007. Standard Review Plan: 3.7.1 Seismic Design Parameters[S]. Washington DC: 1–9.
U.S. Nuclear Regulatory Commission. 2014. Standard Review Plan: 3.7.1 Seismic Design Parameters[S]. Washington DC: 1–10.
-
期刊类型引用(3)
1. 赵云丽，李冉. 考虑风险极限的建筑钢结构抗震延性检测仿真. 计算机仿真. 2024(08): 562-566 . 
百度学术
2. 王子英，王博远，薛廿禧，肖凯. 基于小波函数的IDA分析在RC框架结构中的应用. 重庆建筑. 2023(08): 42-44 . 百度学术
3. 李晓莉，赵月敏，邹积娜，王东升. 基于小波变换的长周期桥梁选波方法研究. 中国地震. 2023(04): 795-809 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 563
- HTML全文浏览量: 140
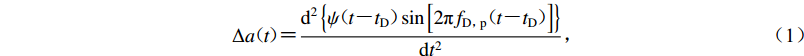
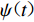
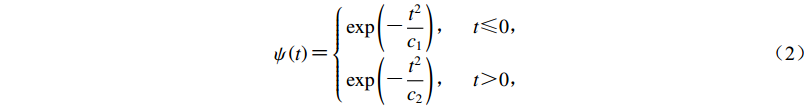
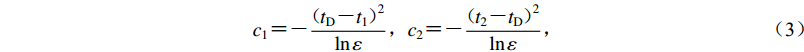
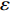
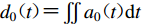
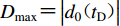
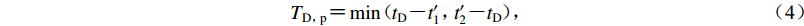
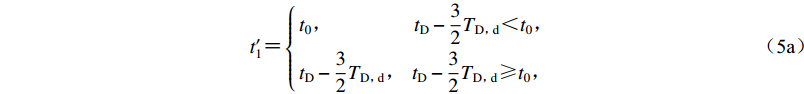
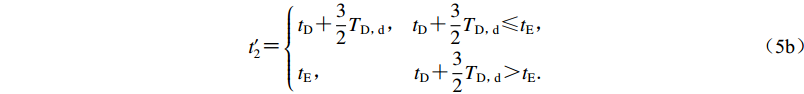
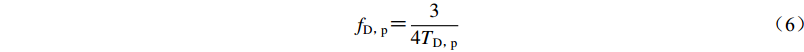
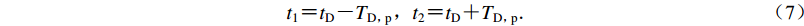
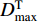
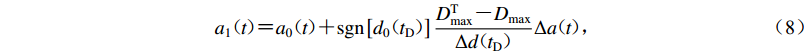
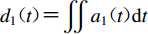
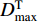
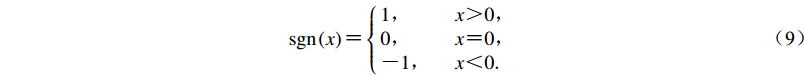
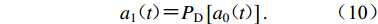
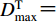
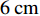
- PDF下载量: 53
- 被引次数: 5
