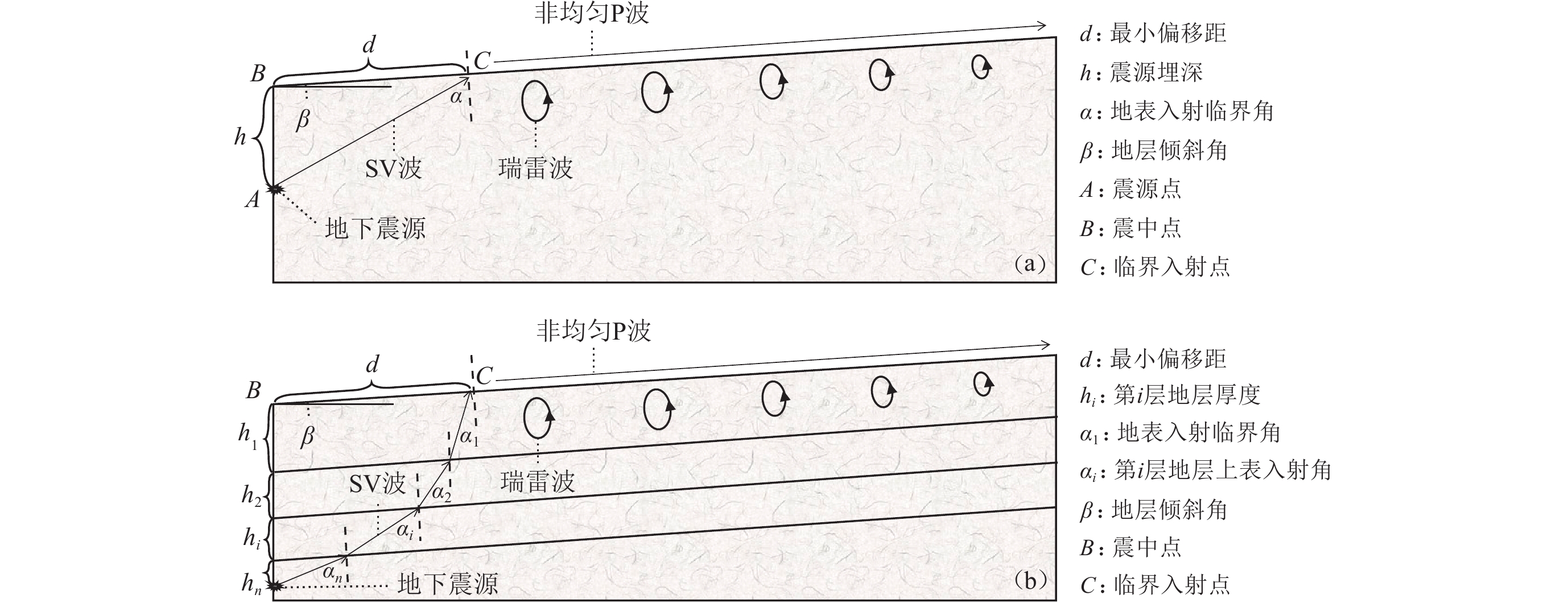
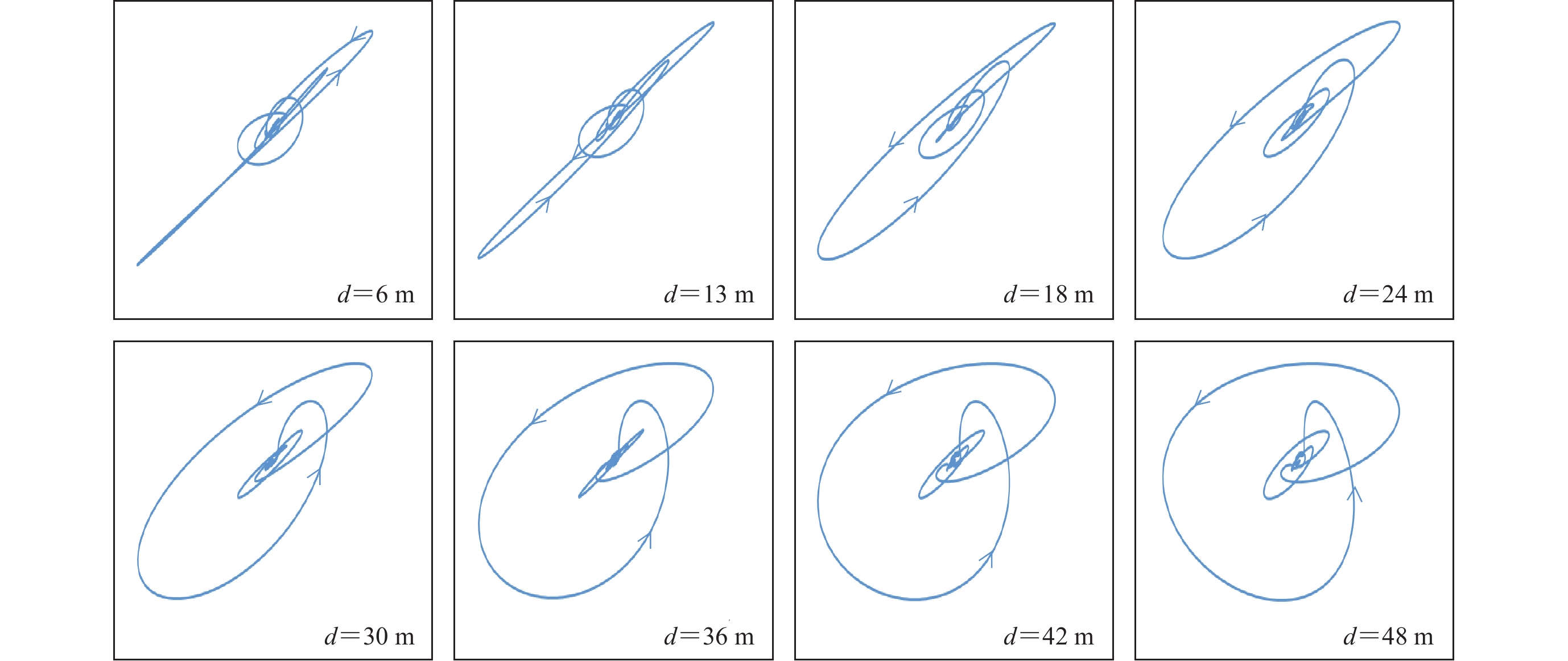
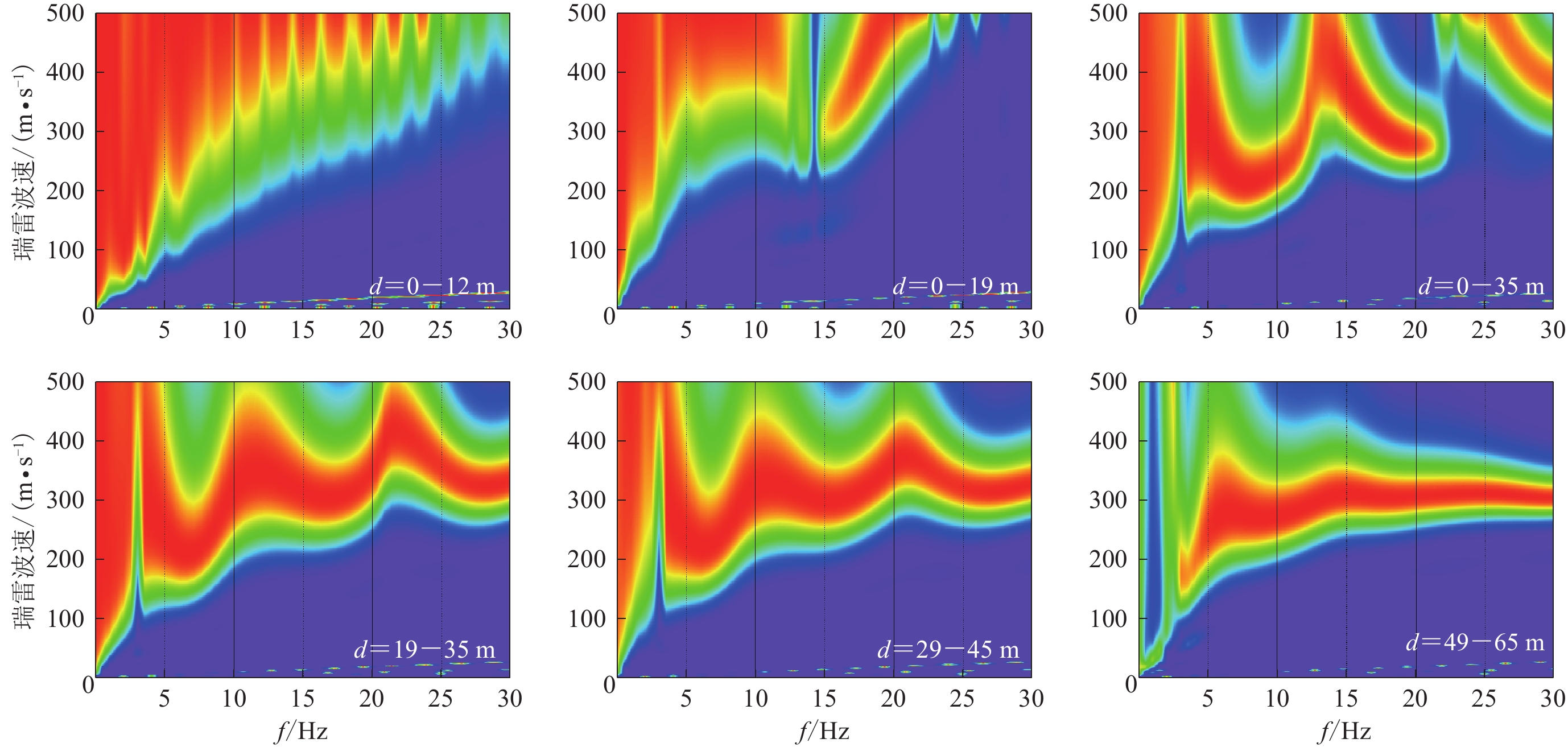
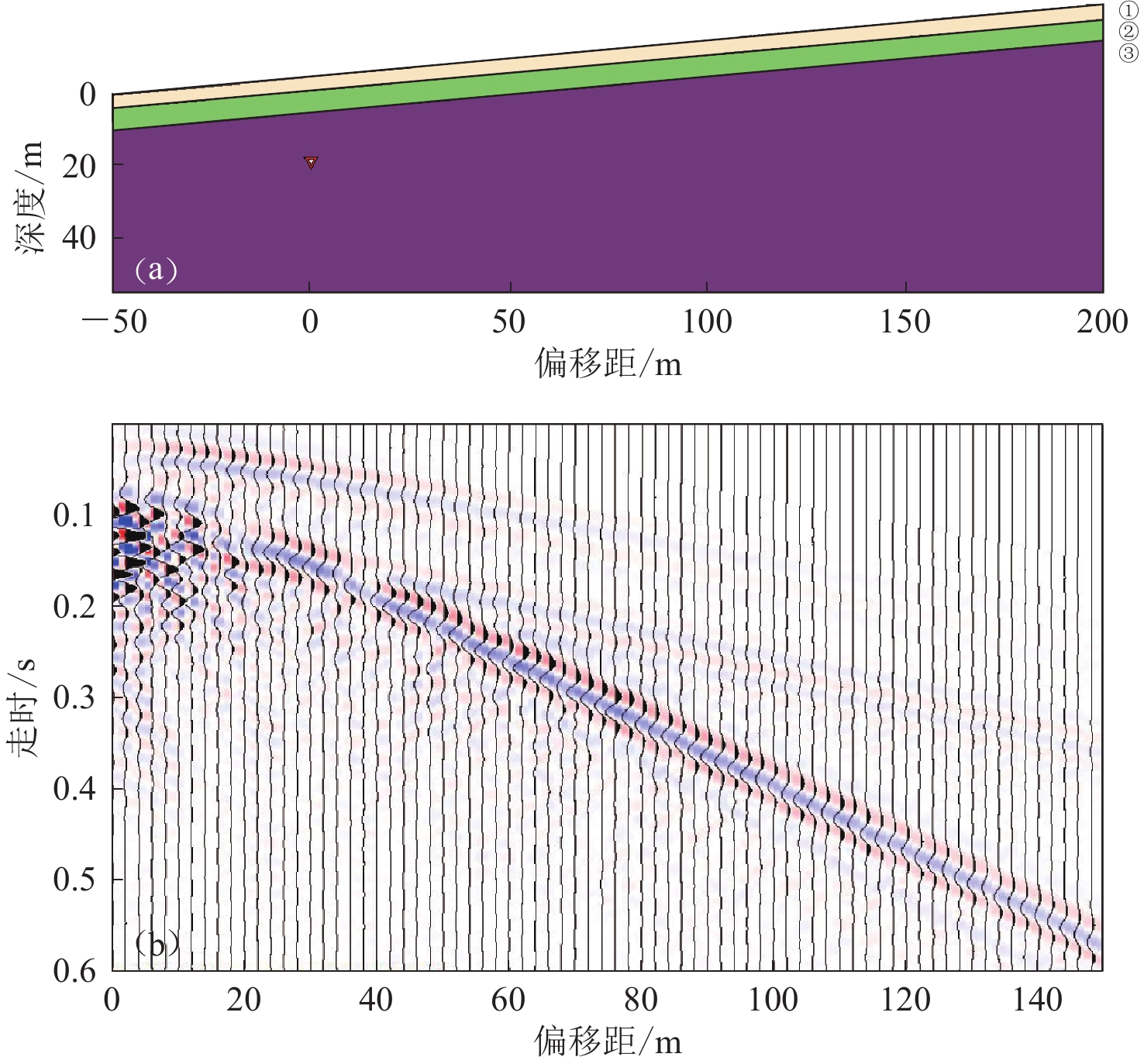
The nearest offset distance estimation method for multi-channel analysis of surface waves in slope
-
摘要: 为减小倾斜边坡中能量较强的近场体波对面波识别的干扰，确保多道面波分析方法接收到的瑞雷波分量具有较强的能量，本文通过分析地下震源在倾斜边坡产生的瑞雷波及其传播规律，基于几何地震学提出了在倾斜地表生成瑞雷波的最小偏移距的经验公式，建立了界面起伏的层状倾斜边坡模型，从而获得模拟共炮点记录，并将基于共炮点记录得到的地表质点运动轨迹、频散计算结果与理论值、估计值进行了对比，结果显示四者具有较强的相关性，由此表明本文提出的最小偏移距估计方法对层状倾斜边坡地表的面波勘探具有一定的指导意义。
-
关键词:
- 多道面波分析方法（MASW） /
- 瑞雷波 /
- 地下震源 /
- 最小偏移距 /
- 边坡响应
Abstract: In order to reduce the interference of energetic near-field body waves to surface wave identification and to ensure Rayleigh wave components with strong energy to be collected by multi-channel analysis of surface waves （MASW） method in the slope, this study firstly analyzed the Rayleigh wave propagation mechanism induced by the underground passive source on the slope. Secondly, based on geometric seismology, an empirical formula for the minimum offset of the Rayleigh wave generated on the sloping surface is proposed, and the layered slope with undulating interface is established so as to obtain the simulated common shot point records. Then by comparing the surface particle motion trajectory and dispersion calculation results obtained from the common shot point records with the theoretical values and estimated values, the results show that the four physical quantities have a strong correlation, which indicates that the proposed minimum offset estimation method in this study can be adopted to guide surface wave exploration of layered slopes.-
Keywords:
- MASW /
- Rayleigh wave /
- underground source /
- minimum offset /
- slope response
-
引言
20世纪六、七十年代，美国、苏联、日本和我国开始研究地震地电学，研究表明电磁现象与地震事件存在一定相关性（Miyakoshi，1986），近年来理论方法方面得到快速发展，而技术方面并没有明显突破（Helman，2020）。我国从20世纪末期开始逐步建设地电场观测台站，目前已经发展为国际上少有的拥有大规模、规范化的地电场观测网的国家，可以实现全面覆盖、时间上连续以及地震危险区重点监测的地电场观测（中国地震学会，2007）。迄今为止，已经记录了丰富的地电场观测资料，促进了利用地电场优势方位角等方法进行地震预报的研究（谭大诚等，2014）。但随着社会的发展，地电场观测台站附近的工农业用电环境越来越复杂，用电过程中若发生对地漏电，势必对地电场观测造成干扰，在原始数据上可能表现为较大的扰动、突变和失真，进而可能影响地电场观测数据的分析和应用。
在地电场观测过程中，常见的干扰有电极极化、雷击、高压直流输电以及测区内外漏电等干扰（李伟等，2014）。当漏电干扰发生时，必须找到干扰源才能消除该干扰，因此如何在短时间内对电磁干扰源进行定位，降低漏电发生对地电场观测的影响，在地电场干扰调查中至关重要。目前，国际上还没有研究者针对干扰源对地电场观测的影响进行专门分析，而国内地电场观测中漏电干扰的定位研究较少，查阅资料仅发现两例实际漏电干扰定位的研究：陈志刚等（2012）利用干扰幅度的矢量合成初步定位干扰源的方位和距离，再结合现场排查来定位干扰源。其方法的优势为应用简便，但该方法的计算结果与现场排查找到的干扰源距离存在较大误差；王福才等（2013）和蒋延林等（2015）结合实地调查、重点走访和分片区停电来定位干扰源。该方法能确保找到干扰源，但需要多部门协调配合，费时费力，难以推广应用。建立偶极源模型进行定位试验的有两例：卫清等（2017）利用多元牛顿迭代算法对漏电位置进行反演，张宇等（2017）提出动态枚举定位求解算法。这两种方法能定位偶极干扰源的两个电极，且精度高，误差仅为数米。但这两个方法的使用有较为严格的限制，要求一个共用电极和另外五个电极，多数地电场观测台站并未与地电阻率测量同场地观测，这种情形下这两种方法均不可用，且这两种方法目前都仅限于试验阶段。
VAN法认为可以用同方向不同极距的地电场比值是否为1来区别近场信号和地震电磁场信号（Varotsos，Alexopoulos，1984）。田山等（2009）认为可以利用长短极距比值的稳定性来分析地震地电场异常信息。这些研究表明同测向长短极距比值具有可应用性，实际地电场观测中，通常会利用同测向长短极距比值是否稳定来分析是否有近场干扰（马钦忠等，2016）。由于不同位置的点源所引起的干扰电场的长短极距比值大小不同，本文提出长短极距比值干扰源定位方法，将漏电干扰源视为地表点源，利用不同测向的比值就可以定位出点源的具体位置。利用该方法定位了徐庄子台漏电干扰源，验证了该方法在地电场观测中能准确定位可视为点源的漏电干扰源，并利用高邮地震台人工干扰源试验观测数据定位干扰源位置，验证了当存在距离近且极距大的偶极源干扰时，能准确定位其中一个电极。
1. 基本原理
我国在进行地电场观测时，通常采用多方向、多极距测量方式，一般为三个测向：东西、南北、北东或北西，在每个观测方向布设长、短两个极距的测道，一共设置6个测道，台站布极如图1所示。
![]()
图 1 我国地电场观测布极方式示意图（a） 十字形布设；（b） L形布设Figure 1. Schematic diagram of the electrode arrangement for our geoelectric field observation（a） Cruciform layout；（b） L-shaped layout建立电阻率均匀各向同性的半空间模型，图2左侧为漏电干扰源与测量电极坐标示意图，xoy平面直角坐标系为地表，其中：红点表示电量为q的干扰源，蓝点表示测量电极，以o点为坐标原点，向东为x轴正向，向北为y轴正向建立坐标系。
![]()
图 2 不同的电极布设坐标示意图（左）、地电场长短极距比值分布图（中）和比值确定时的等值线图（右）（a） 十字形东西向；（b） L形东西向；（c） L形北东向Figure 2. Schematic diagram of different electrode layout coordinates （left），distribution of the long and short pole distance ratio for geoelectric field （middle），and contour map when the ratio is determined （right）（a） Cross-shaped east-west direction；（b） L-shaped east-west direction； （c） L-shaped north-east direction干扰源在测量电极处产生的电势为：
$$ U ＝ \frac{{kq}}{r}，$$ (1) 式中，$k$为在均匀半无限空间中的比例系数，为常数，其值与均匀介质的介电常数相关。
电场强度的计算公式为：
$$ E ＝ \frac{{{U_1} － {U_2}}}{L}\text{，} $$ (2) 式中，${U_1}$为干扰源在测量电极1处产生的电势，${U_2}$为干扰源在测量电极2处产生的电势，$L$为两测量电极间的距离。将式（1）代入式（2）有：
$$ E ＝ \left(\frac{{kq}}{{{r_1}}} － \frac{{kq}}{{{r_2}}}\right) {\text{×}} \frac{1}{L} \text{，} $$ (3) 式中${r_1}$和${r_2}$分别为干扰源到两个测量电极的距离。
将长极距的测量电极坐标$ （ {x_{{\rm{L}}1}}， {y_{{\rm{L}}1}} ） $，$ （ {x_{{\rm{L}}2}}， {y_{{\rm{L}}2}}$）和干扰源坐标$ （ {x}_{0}， {y}_{0}$）带入式（3）：
$$ {E_{\rm{L}}} ＝ \left( {\frac{{kq}}{{\sqrt {{{ （ {x_0} － {x_{{\rm{L}}1}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{L}}1}} ） }^2}} }} － \frac{{kq}}{{\sqrt {{{ （ {x_0} － {x_{{\rm{L}}2}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{L}}2}} ） }^2}} }}} \right) {\text{×}} \frac{1}{{\sqrt {{{ （ {x_{{\rm{L}}1}} － {x_{{\rm{L}}2}} ） }^2} ＋ {{ （ {y_{{\rm{L}}1}} － {y_{{\rm{L}}2}} ） }^2}} }} ； $$ (4) 将短极距的测量电极坐标$ （ {x_{{\rm{S}}1}}， {y_{{\rm{S}}1}} ） $、$ （ {x_{{\rm{S}}2}}， {y_{{\rm{S}}2}} ） $和干扰源坐标$ （ {x}_{0}， {y}_{0} $）带入式（3）：
$$ {E_{\rm{S}}} ＝ \left( {\frac{{kq}}{{\sqrt {{{ （ {x_0} － {x_{{\rm{S}}1}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{S}}1}} ） }^2}} }} － \frac{{kq}}{{\sqrt {{{ （ {x_0} － {x_{{\rm{S}}2}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{S}}2}} ） }^2}} }}} \right) {\text{×}} \frac{1}{{\sqrt {{{ （ {x_{{\rm{S}}1}} － {x_{{\rm{S}}2}} ） }^2} ＋ {{ （ {y_{{\rm{S}}1}} － {y_{{\rm{S}}2}} ） }^2}} }} \text{.} $$ (5) 计算上述长极距测得的电场值和短极距测得的电场值的比值：
$$ \dfrac{{{E_{\rm{L}}}}}{{{E_{\rm{S}}}}} ＝ \dfrac{{\left( {\dfrac{1}{{\sqrt {{{ （ {x_0} － {x_{{\rm{L}}1}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{L}}1}} ） }^2}} }} － \dfrac{1}{{\sqrt {{{ （ {x_0} － {x_{{\rm{L}}2}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{L}}2}} ） }^2}} }}} \right) {\text{×}} \dfrac{1}{{\sqrt {{{ （ {x_{{\rm{L}}1}} － {x_{{\rm{L}}2}} ） }^2} ＋ {{ （ {y_{{\rm{L}}1}} － {y_{{\rm{L}}2}} ） }^2}} }}}}{{\left( {\dfrac{1}{{\sqrt {{{ （ {x_0} － {x_{{\rm{S}}1}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{S}}1}} ） }^2}} }} － \dfrac{1}{{\sqrt {{{ （ {x_0} － {x_{{\rm{S}}2}} ） }^2} ＋ {{ （ {y_0} － {y_{{\rm{S}}2}} ） }^2}} }}} \right) {\text{×}} \dfrac{1}{{\sqrt {{{ （ {x_{{\rm{S}}1}} － {x_{{\rm{S}}2}} ） }^2} ＋ {{ （ {y_{{\rm{S}}1}} － {y_{{\rm{S}}2}} ） }^2}} }}}} \text{.} $$ (6) 从式（6）可以看出，地电场长短极距比值EL/ES与干扰源的电量q无关，仅与各测量电极的坐标和干扰源的坐标$ （ {x_0}， {y_0} ） $有关。地电场台站中各测向的长短极距测量电极的坐标固定，所以只需知道干扰源的坐标，将其代入式（6）就可以计算出该干扰源引起的各测向地电场长短极距增量的比值。
我们将o点作为坐标原点，正北为y轴正方向，正东为x轴正方向，建立坐标系，固定长短极距测量电极的坐标。以图2a为例，此时东西向长极距测量电极A1，A2和短极距测量电极坐标A1 ′，A2 ′已知，那么某一处存在干扰源时，将该干扰源坐标带入式（6），便可计算干扰引起的地电场长短极距增量的比值。将原点附近2 km范围内按4 m间隔进行网格划分，计算仅每个网格点处存在干扰源时引起的东西向长短极距测道所产生的增量的比值，并将比值以不同颜色表示，得到图2a所示的地电场长短极距比值分布图。我们采用Python语言编写该程序，计算并绘制此图用时1.27 s，说明该方法计算速度快。由于该方法在干扰源的计算公式推导过程中时并未假设长短极距测道同方向，所以该方法并不仅限于同方向的两测道的比值计算，不同方向不同测道的数据也可用该方法计算干扰源的位置。当漏电干扰出现时，我们选取干扰前后的数据作差，分别计算干扰导致长极距和短极距的地电场增量，然后计算地电场长短极距增量的比值，在分布图中只画出该比值的等值线，那么该等值线上每一个坐标点都是干扰源可能的坐标点。
图2a左图为十字形东西向长短极距电极布设方式坐标示意图，图2a中间图是将图2a左图中的坐标点带入式（6）计算得到的十字形东西向地电场长短极距比值分布图，可以看出比值关于x轴和y轴对称，在两条45°对角线上比值接近于1，2 km以外存在干扰源时，比值接近于1。当确定比值为1.2时，即从图2a中间图中仅选出值为1.2的等值线（图2a右图），图中红线上每一个坐标点都可能是干扰源所在的坐标点。
图2b显示：地电场长短极距比值关于x轴轴对称，在两条30—40°的对角线上比值接近于1。当确定比值为0.8时，即从图2b中间图仅选出值为0.8的等值线（图2b右图），图中红线上每一个坐标点都可能是干扰源所在的坐标点。
图2c显示：地电场长短极距比值关于北西对角线对称，在北东对角线上比值接近于1。当确定比值为0.9时，即从图2c中间图仅选出值为0.9的等值线（图2c右图），图中蓝线上每一个坐标点都可能是干扰源所在的坐标点。
实际地电场观测中发生漏电干扰时，我们计算不同测向的地电场长短极距比值，将不同测线计算得到的可能的坐标点画在同一个图中，交点便是干扰源可能存在的位置。假设地电场观测布极方式为如图2b和2c的L形布设，且东西向比值为0.8，北东向比值为0.9，将两测向的等值线画在一个坐标系中（图3），可以看到有两个交点，那么这两个交点即为干扰源可能的位置。
![]()
图 3 长短极距比定位漏电干扰源示意图Figure 3. Schematic diagram of locating leakage interference source by long-and-short polar distance ratio从图3可以看出交点可能不止一个，那么需要利用以下两个方法排除不可能的坐标点：① 通过观察其它测向是否有干扰来排除近处的交点。② 结合各测向的地电场干扰的增减同步性来判断，即南北向和东西向地电场值同增同减时，干扰源在两测线所夹的象限或者斜对面的象限；南北向和东西向地电场值增减相反时，干扰源在另外两象限。
漏电电流分为直流电和交流电，本文仅讨论直流漏电干扰。在理想状况下，漏电发生时，电场表现为方波状，即：漏电前，电场保持不变；漏电时刻，电场突增；漏电持续时，电场维持不变；漏电消失时刻，电场突降。方波从低值到高值的增量是漏电干扰产生的电场值。但由于数据采集只能采集一定频率范围内的信号，漏电前后会出现吉布斯现象，即在方波脉冲的转折处会有明显的震荡。除了震荡的转折处，在其它时刻我们可以得到稳定的低值和高值，所以为了提高结果的准确性，应该选数据相对稳定期间的低值和高值来计算增量并以此作为漏电干扰产生的电场值。日常地电场数据采集过程中，分钟值是一分钟之内进行多次采样后平均得来，虽然在一定程度上消除了漏电前后吉布斯现象的影响，但由于一分钟之内地电场变化较大，数据表现出不稳定性，在干扰出现前后，无法确定稳定的高值和低值，所以选择不同时刻的数据会导致干扰源的定位结果不同。我们认为应该通过提高采样率来避免地电场变化对干扰源定位的影响，并选择震荡转折以外稳定的高值和低值来计算增量，以避免吉布斯现象的影响，从而提高该方法的准确性。
2. 点干扰源的定位应用
徐庄子台地电场电极布设方式为L型，各测量电极位置如图4所示，建立以o点为坐标原点，向东为x轴正向，向北为y轴正向的坐标轴，东西向测线和南北向测线所夹的象限为第三象限。2009年11月，徐庄子台的地电场观测数据出现方波干扰。图5为2010年11月16日徐庄子台地电场分钟数据对比曲线，可以看出在18时和21时左右，南北向和东西向同时发生了方波状漏电干扰，且长短极距测得的地电场干扰幅度成一定比值，而北西向没有明显干扰。
![]()
图 4 徐庄子地震台地电场观测系统电极布置方式示意图 （单位：m）Figure 4. The sketch map of layout patterns for electrodes in geoelectric field observatory systems at Xuzhuangzi seismic station （unit：m）![]()
图 5 徐庄子台2010年11月16日地电场分钟数据对比曲线Figure 5. Comparison curves of minute data of geoelectric field at Xuzhuangzi station on November 16，201011月出现了多次干扰事件，每次干扰事件各测向的长短极距增量比值差别不大，表现在干扰源坐标上的差别仅为几米，可以忽略不计，因此本文直接采用了陈志刚等（2012）在文章中随机挑选的11月中的5次干扰事件的东西向和南北向的长短极距的地电场值（表1），分别计算了这5次干扰事件的长短极距比，并求得它们的平均值。由于北西向地电场数据未表现出明显干扰，文中只使用了南北和东西测向的值。
表 1 徐庄子台干扰电场长短极距比Table 1. Long-and-short polar distance ratio of interference electric field at Xuzhuangzi station利用东西向和南北向长短极距比的平均值画图，如图6，黑线和红线有五个交叉点，因此需要结合其它条件进行排除。东西向测线和南北向测线所夹的象限为第三象限，从图5可以看出，东西向和南北向的电场干扰同增同减，干扰源应在两测线之间象限或者斜对面的象限，即第三象限或第一象限。因北西向地电场不受干扰，最终认定干扰源位于红圈所示的这一交叉点，其坐标为（250，400），方位为北偏东32°，距离o点471.7 m。最后经实地确认，干扰源为台站东北方、距离台站500 m的木材加工厂的电器供暖设备漏电，与文中计算得到的471.7 m相差约30 m，且方位与最终排查得到的干扰源方位相近。
![]()
图 6 徐庄子台干扰源定位结果示意图Figure 6. Schematic diagram of the location result of the interference source at Xuzhuangzi station陈志刚等（2012）的文章中利用矢量合成方法计算的方位角为北偏东43°，本文计算结果为北偏东32°。我们认为利用矢量合成的方法初步确定干扰源的方位和距离不可靠：一方面，出现干扰源时地电场值是有增有减的，不能因此推论干扰源在东北方向；另一方面，漏电干扰为近源，徐庄子台的电极布设方式为L型，不能简单的将东西向和南北向的干扰电场近似为o点的电场。
3. 偶极干扰源的定位应用
2016年6月卫清等（2017）和张宇等（2017）在高邮台地电观测场地进行人为对地供电试验，模拟偶极源漏电对地电场观测的干扰，用来验证牛顿迭代反演法和动态枚举法是否能准确定位干扰源。由于干扰源离测量电极很近、且极距大，因此不可看作点源，需要找出两个电极所在的位置。我们利用该文章中的数据研究长短极距比值法在偶极干扰源试验中的计算效果。图7为高邮地电观测布极图，建立以o点为坐标原点，向东为x轴正向，向北为y轴正向的坐标轴。将地电阻率供电电极${A_1}$和${B_1}$设为偶极干扰源，东西测向的长极距测道为a1o、短极距测道为a2o；南北测向的长极距测道为b1o、短极距测道为b2o；斜测向的长极距测道为M3o、短极距测道为N1o。我们需要利用这三个测向的长短极距比值来定位干扰源${A_1}$和${B_1}$的坐标。
![]()
图 7 高邮地震台地电场及地电阻率同场观测电极布极图（单位：m）Figure 7. The sketch map of layout patterns for electrodes in geoelectric field and earth resistivity observatory systems at Gaoyou seismic station （unit：m）利用张宇等（2017）文章中提供的人工干扰源试验电位差值ΔV和对应测道的极距长度L带入电场强度公式E＝ΔV/L，计算得到长短极距的地电场及其比值（表2）。由于是试验数据，采样率高，数据质量高，电场值随时间的变化呈较为标准的方波形态，选取方波从低值到高值突变时刻的数据。从三次试验的各测向长短极距比值大小基本一致可以看出，在采样率高、数据质量高的情况下，长短极距比值稳定也证明了长短极距比值能反应干扰源的位置。
表 2 偶极源试验中干扰电场长短极距比Table 2. Long-and-short polar distance ratio of interference electric field in dipole source test图8为将表2中的三个测向的长短极距比平均值的等值线画在一幅图中，其中三个交点为干扰源可能的坐标点。实际的${A_1}$电极的坐标为（303，−420），计算得到的坐标为（291，−410），相差约20 m。实际的${B_1}$电极的坐标为（303，579），该电极在另外两个交点（288，654）和（306，182）之间，说明该方法用于计算偶极干扰源时也能有效定位其中一个电极。也说明在地电阻率与地电场同地观测的情况下，出现漏电干扰时，可以记录地电阻率法的测量电极的电位值，计算长短极距比作为另一测向数据，从而更准确地定位干扰源。
![]()
图 8 偶极干扰源试验定位结果示意图Figure 8. Schematic diagram of the location results of the dipole interference source test4. 结论
尽管对地漏电在地电场观测过程中并不常见，但漏电一旦发生，将严重影响地电场观测数据，所以快速定位干扰源，排除干扰，对地电场观测意义重大。本工作提出长短极距比值法定位电磁干扰源，并应用到两个实例中，得到了较好的应用效果。
本方法的实际应用结果表明：① 当干扰源极距较小可以看作点源时，计算得到的干扰源位置较为准确，可以为排查干扰节省成本；② 当干扰源距离测量电极很近，且干扰源极距较大时，干扰源不可看作点源，该方法可以有效定位其中一个电极，再通过现场排查来确定干扰源的两极。长短极距比值法利用数据库提供的各测向的地电场分钟值就能定位漏电干扰源，应用简便，投入实际应用中可以大大缩小排查范围。
-
![]()
图 1 倾斜边坡示意图
（a） 上倾边坡；（b） 下倾边坡
Figure 1. Schematic diagram of slopes
（a） Updip slope；（b） Downdip slope
![]()
图 2 单层（a）与多层（b）上倾边坡示意图
Figure 2. Schematic diagram of single-layer （a） and multi-layer （b） updip slopes
![]()
图 3 单层（a）与多层（b）下倾边坡示意图
Figure 3. Schematic diagram of a single-layer （a） and multi-layer （b） downdip slopes
![]()
图 4 多层水平地层示意图（a）及其共炮点记录（b）
Figure 4. Schematic diagram of a multi-layer horizontal strata （a） and its common shot point gathers （b）
![]()
图 5 不同偏移距d下水平地层地表的质点偏振图
Figure 5. Polarization map of surface particles in horizontal strata with different offset d
![]()
图 6 不同偏移距d范围内的水平地层频散计算图
Figure 6. Dispersion calculation diagram of horizontal strata with different offset d
![]()
图 7 多层上倾边坡示意图（a）及其共炮点记录（b）
Figure 7. Schematic diagram of a multi-layer updip slope （a） and its common shot point gathers （b）
![]()
图 8 不同偏移距d范围内上倾边坡地表质点偏振图
Figure 8. Polarization map of surface particles on updip slope with different offset d
![]()
图 9 不同偏移距d范围内的上倾边坡频散计算图
Figure 9. Dispersion calculation diagram of updip slope with different offset d
![]()
图 10 多层下倾边坡示意图（a）及其共炮点记录（b）
Figure 10. Schematic diagram of a multi-layer downdip slope （a） and its common shot point gathers （b）
![]()
图 11 不同偏移距d范围内下倾边坡地表质点偏振图
Figure 11. Polarization map of surface particles on downdip slope with different offset d
![]()
图 12 不同偏移距d范围内的下倾边坡频散计算图
Figure 12. Dispersion calculation diagram of downdip slope with different offset d
表 1 本文所用模型的地层参数
Table 1 Stratum parameters of the models used in this study
层位 厚度/m vP/（m·s−1） vS/（m·s−1） ① 4 480 200 ② 6 600 247 ③ 半无限空间 750 294 注：地层③因倾斜角度从左至右厚度变化，不作统计。 
下载: 导出CSV
-
陈浩朋,朱良保,叶庆东,王清东. 2012. 多地震叠加提取双台间面波频散信息[J]. 地震学报,34(6):773–784. doi: 10.3969/j.issn.0253-3782.2012.06.004 Chen H P,Zhu L B,Ye Q D,Wang Q D. 2012. Measurement of inter-station surface wave dispersion using multi-earthquake data stacking[J]. Acta Seismologica Sinica,34(6):773–784 (in Chinese).
房立华,吴建平,王未来,王长在,杨婷. 2013. 华北地区勒夫波噪声层析成像研究[J]. 地球物理学报,56(7):2268–2279. doi: 10.6038/cjg20130714 Fang L H,Wu J P,Wang W L,Wang C Z,Yang T. 2013. Love wave tomography from ambient seismic noise in North-China[J]. Chinese Journal of Geophysics,56(7):2268–2279 (in Chinese).
冯梅,安美建,van der Lee S. 2008. 利用面波波形模拟探测中国大陆地壳和上地幔波速结构的分区特征[J]. 地震学报,30(2):114–122. doi: 10.3321/j.issn:0253-3782.2008.02.002 Feng M,An M J,van der Lee S. 2008. Region-related features of crustal and upper-mantle velocity structure of the Chinese mainland detected by surface waveform modeling[J]. Acta Seismologica Sinica,30(2):114–122 (in Chinese).
李白基,李宁,陈虹. 1989. 南北地震带和两侧的瑞利面波群速度差异及其大地构造意义[J]. 地震学报,11(3):268–274. Li B J,Li N,Chen H. 1989. Group velocity differences of Rayleigh waves between the NS seismic belt,China,and the side regions,and their tectonic implications[J]. Acta Seismologica Sinica,11(3):268–274 (in Chinese).
刘康,戴靠山,许强,翁渝峰,黄李观,赵逍,游庆瑜. 2018. 埋入源多道面波分析(MASW)中最小偏移距的估计方法[J]. 地球物理学报,61(6):2421–2432. doi: 10.6038/cjg2018L0285 Liu K,Dai K S,Xu Q,Weng Y F,Huang L G,Zhao X,You Q Y. 2018. Nearest offset design for multichannel analysis of surface waves (MASW) method with buried source excitations[J]. Chinese Journal of Geophysics,61(6):2421–2432 (in Chinese).
刘庆华,鲁来玉,王凯明. 2015. 主动源和被动源面波浅勘方法综述[J]. 地球物理学进展,30(6):2906–2922. doi: 10.6038/pg20150660 Liu Q H,Lu L Y,Wang K M. 2015. Review on the active and passive surface wave exploration method for the near-surface structure[J]. Progress in Geophysics,30(6):2906–2922 (in Chinese).
沈玉松,康英. 2014. 广东及其邻域噪声面波层析成像[J]. 地震学报,36(5):826–836. Shen Y S,Kang Y. 2014. Surface wave tomography of Guangdong and its adjacent areas from ambient seismic noise[J]. Acta Seismologica Sinica,36(5):826–836 (in Chinese).
王小龙,马胜利,郭志,雷兴林,夏英杰,郭欣,余国政,勾宪斌,蒋霞东. 2013. 利用地震背景噪声成像技术反演三峡库区及邻近地区地壳剪切波速度结构[J]. 地球物理学报,56(12):4113–4124. doi: 10.6038/cjg20131216 Wang X L,Ma S L,Guo Z,Lei X L,Xia Y J,Guo X,Yu G Z,Gou X B,Jiang X D. 2013. S-wave velocity of the crust in Three Gorges Reservoir and the adjacent region inverted from seismic ambient noise tomography[J]. Chinese Journal of Geophysics,56(12):4113–4124 (in Chinese).
席超强. 2017. 复杂地形条件下面波探查技术研究与应用[D]. 淮南: 安徽理工大学: 47–49. Xi C Q. 2017. Surface Wave Detection Research and Application Technology of Complex Terrain Condition[D]. Huainan: Anhui University of Science and Technology: 47–49 （in Chinese）.
夏江海,高玲利,潘雨迪,沈超,尹晓菲. 2015. 高频面波方法的若干新进展[J]. 地球物理学报,58(8):2591–2605. doi: 10.6038/cjg20150801 Xia J H,Gao L L,Pan Y D,Shen C,Yin X F. 2015. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics,58(8):2591–2605 (in Chinese).
Aki K. 1957. Space and time spectra of stationary stochastic waves,with special reference to microtremors[J]. Bull Earthq Res Inst Tokyo,35:415–456.
Capon J. 1970. Applications of detection and estimation theory to large array seismology[J]. Proc IEEE,58(5):760–770. doi: 10.1109/PROC.1970.7730
Chai H K,Momoki S,Aggelis D G,Shiotani T. 2010. Characterization of deep surface-opening cracks in concrete:Feasibility of impact-generated Rayleigh-waves[J]. Mater J,107(3):305–311.
Cristini P,Komatitsch D. 2012. Some illustrative examples of the use of a spectral-element method in ocean acoustics[J]. J Acoust Soc Am,131(3):EL229–EL235. doi: 10.1121/1.3682459
Dai K S,Liu K,Li X F,You Q Y,Tang H S,Xu Q. 2019. Application of passive multichannel analysis of surface waves method at sites close to underground railways:Problems and a case study[J]. Appl Geophys,164:191–199. doi: 10.1016/j.jappgeo.2019.03.009
Dikmen Ü,Arısoy M Ö,Akkaya İ. 2010. Offset and linear spread geometry in the MASW method[J]. J Geophys Eng,7(2):211–222. doi: 10.1088/1742-2132/7/2/S07
Ewing W M,Jardetzky W S,Press F,Beiser A. 1957. Elastic waves in layered media[J]. Physics Today,10(12):2.
Haskell N A. 1953. The dispersion of surface waves on multilayered media[J]. Bull Seismol Soc Am,43(1):17–34. doi: 10.1785/BSSA0430010017
Isaacs R P. 1941. The finite differences of polygenic functions[J]. Bull Am Math Soc,47(6):6.
Jones R. 1958. In-situ measurement of the dynamic properties of soil by vibration methods[J]. Géotechnique,8(1):1–21.
Komatitsch D,Barnes C,Tromp J. 2012. Wave propagation near a fluid‐solid interface:A spectral‐element approach[J]. Geophysics,65(2):623–631.
Lay T, Wallace T C. 1995. Modern Global Seismology[M]. California: Academic Press: 98−105.
Malavika V A,Asraff A K,Kumar M,Sofi A. 2021. Fracture analysis of plates and shells using FEM and XFEM[J]. Innovat Infrastruct Solut,6(1):43. doi: 10.1007/s41062-020-00439-z
Park C B,Miller R D. 2008. Roadside passive multichannel analysis of surface waves (MASW)[J]. J Environ Eng Geophys,13(1):1–11. doi: 10.2113/JEEG13.1.1
Rayleigh L. 1885. On waves propagated along the plane surface of an elastic solid[J]. Proc Lond Math Soc,17(1):4–11. doi: 10.1112/plms/s1-17.1.4
Stokoe K H, Wright S G, Bay J A, Roesset J M. 1994. Characterization of geotechnical sites by SASW method[G]//Geophysical Characterization of Sites. New Delhi: Oxford Publishers: 15–25.
Xu Y X,Xia J H,Miller R D. 2006. Quantitative estimation of minimum offset for multichannel surface-wave survey with actively exciting source[J]. J Appl Geophys,59(2):117–125. doi: 10.1016/j.jappgeo.2005.08.002
Zhang S X,Chan L S,Xia J H. 2004. The selection of field acquisition parameters for dispersion images from multichannel surface wave data[J]. J Pure Appl Geophys,161(1):185–201. doi: 10.1007/s00024-003-2428-7
-
期刊类型引用(6)
1. 罗肖，程谦恭，王玉峰，李天话. 粒径对岩崩-碎屑流滑震特征的影响. 地球科学与环境学报. 2023(01): 118-130 . 
百度学术
2. 白雪松，赵洲，杨泽. 基于数值方法的不稳定斜坡地震响应研究. 能源与环保. 2023(12): 204-210 . 百度学术
3. 马星宇，王兰民，马文国，柴少峰，赖欲儒. 不同设防烈度下西吉黄土动抗剪强度特征研究. 岩土工程学报. 2023(S2): 153-158 . 百度学术
4. 刘平，徐政伟，罗奇峰. 我国大陆地区地震动衰减关系研究进展. 地震学报. 2022(05): 797-809 . 本站查看
5. 肖亮，俞言祥. 我国大陆地区常用浅壳地震的地震动参数衰减关系. 地震学报. 2022(05): 752-764 . 本站查看
6. 赵海军，马凤山，李志清，郭捷，张家祥. 基于Newmark模型的概率地震滑坡危险性模型参数优化与应用:以鲁甸地震区为例. 地球科学. 2022(12): 4401-4416 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 424
- HTML全文浏览量: 153
- PDF下载量: 37
- 被引次数: 8
