Rapid magnitude estimation based on multi-input Gaussian process regression
-
摘要:
为充分利用初至地震波中与震级相关的信息，提高震级估算精度，本文提出了一种震级快速估算方法（GPR），该方法将初至地震波在时域、频域和时频域中的10个特征参数输入高斯过程回归模型实现震级估算。利用日本的大量地表强震记录对GPR方法进行训练和测试，并与最大卓越周期${\tau ^{\max }_{\mathrm{p}}} $方法和位移幅值P d方法进行了对比。结果表明，GPR方法在有震源距和无震源距两种情况下，估算震级的准确性均显著好于${\tau ^{\max }_{\mathrm{p}}} $方法和P d方法。此外，利用智利的地表强震记录对日本数据训练的GPR进行泛化能力测试的结果显示，GPR方法较${\tau ^{\max }_{\mathrm{p}}} $方法和P d方法具有更好的泛化能力。利用GPR方法对我国的三次典型震例进行震级估算，验证该方法是合理且可靠的，表明GPR方法不会受到地域差异的影响，可以有效提高地震预警系统估算震级的准确度。
Abstract:Accurate and rapid magnitude estimation is of paramount importance for earthquake early warning systems （EEWs）. Traditional magnitude estimation methods based on a single characteristic parameter of the initial seismic wave are widely used in EEWs. However, these empirical formulae, established by a single characteristic parameter, fail to fully exploit the information related to magnitude contained in the initial seismic wave, significantly limiting the effectiveness of magnitude estimation. To improve the accuracy of magnitude estimation in EEWs, this paper proposes a Gaussian process regression （GPR） based method that can estimate magnitudes in both scenarios: with and without hypocentral distance. The proposed method, GPR-M, uses multiple characteristic parameters from the time domain, frequency domain, and time-frequency domain as inputs, while GPR-M-R incorporates hypocentral distance. Both methods estimate magnitude by integrating various aspects of information from the initial seismic wave. The study utilized
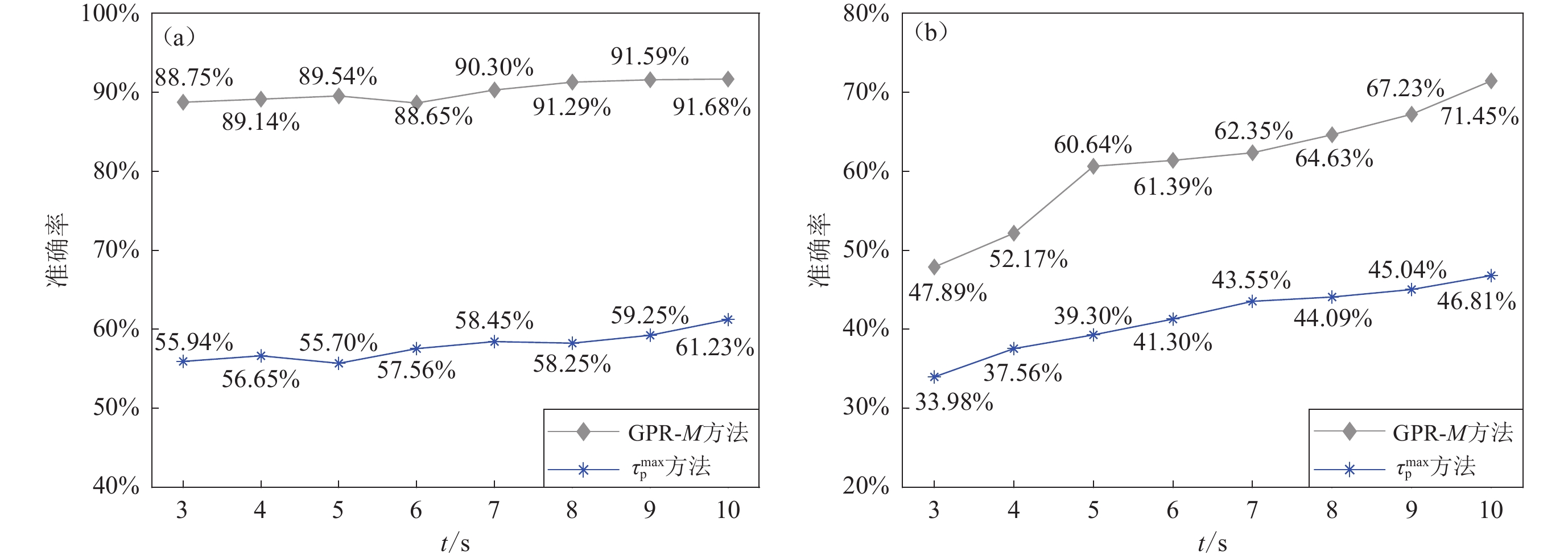
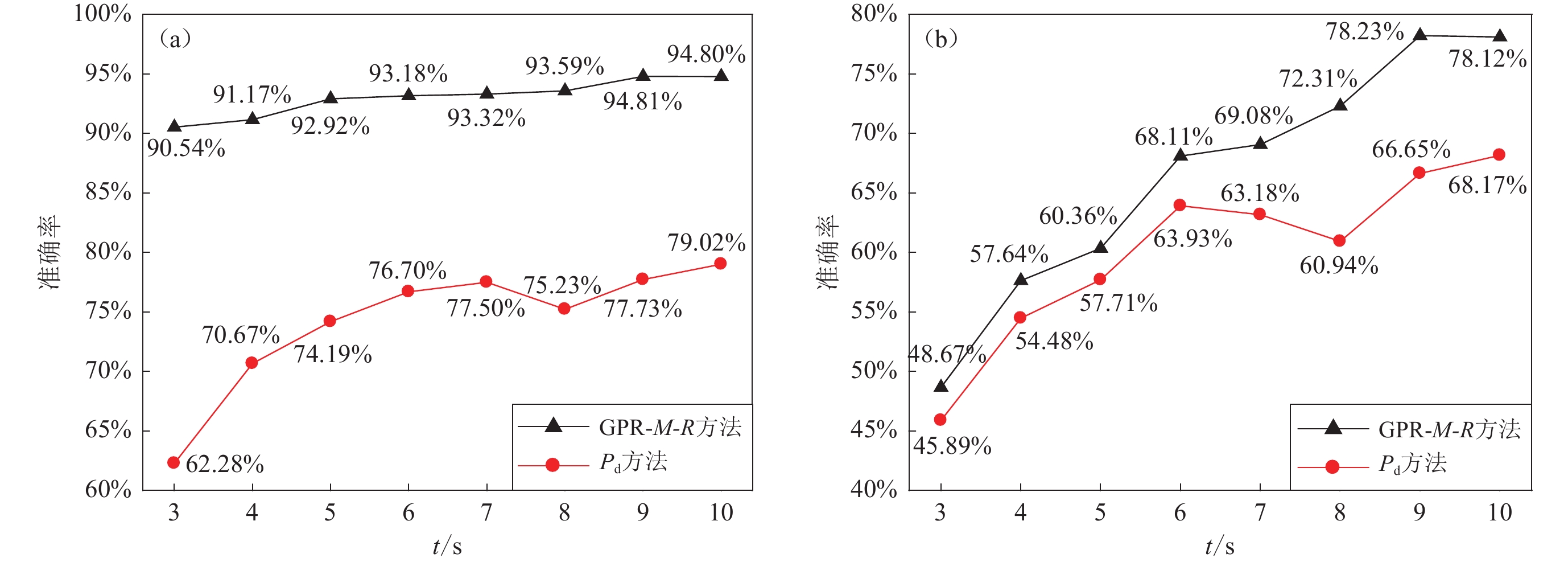
33698 vertical acceleration records from the Japanese Kiban-Kyoshin Network （KiK-net） for training and testing, and5353 vertical acceleration records from the Chilean Simulation Based Earthquake Risk and Resilience of Interdependent Systems and Networks （SIBER-RISK） for generalization testing. Additionally, the method’s practical application was validated using three typical earthquake cases in China, with MS5.4, MS6.4, and MS8.0. The performance of the GPR method was compared with the widely adopted ${\tau ^{\max }_{\mathrm{p}}} $ and P d methods. The test results from the Japanese records indicate that for initial seismic waves of 3 to 10 s, both GPR-M and GPR-M-R outperform the ${\tau ^{\max }_{\mathrm{p}}} $ and P d methods in magnitude estimation. Specifically, the standard deviation of estimation errors for the GPR-M method is reduced by approximately 52.53% to 61.20% compared with the ${\tau ^{\max }_{\mathrm{p}}} $ method, while the GPR-M-R method reduces the standard deviation of estimation errors by about 37.72% to 41.21% compared with the P d method. For larger earthquakes （MW≥6.5）, the magnitude saturation phenomenon is less pronounced in the GPR-M and GPR-M-R methods compared with the ${\tau ^{\max }_{\mathrm{p}}} $ and P d methods. The accuracy of magnitude estimation for MW≥6.5 is improved by 1.4 to 1.5 times with the GPR-M method compared with the ${\tau ^{\max }_{\mathrm{p}}} $ method, and by 1.2 to 1.45 times with the GPR-M-R method compared with the P d method. The test results from the Chilean data demonstrate that both the GPR-M and GPR-M-R methods can effectively estimate earthquake magnitudes in Chile. The standard deviation of estimation errors for the GPR-M method is reduced by approximately 53.08% to 55.13% compared with the ${\tau ^{\max }_{\mathrm{p}}} $ method, and the GPR-M-R method reduces the standard deviation of estimation errors by about 35.88% to 36.59% compared with the P d method, showing excellent generalization capability. The test results from the three Chinese earthquake cases further confirmed that the GPR methods exhibit better accuracy and reliability compared with the ${\tau ^{\max }_{\mathrm{p}}} $ and P d methods. The GPR method can significantly improve the accuracy of magnitude estimation in EEWs and is not affected by regional differences. In conclusion, this study presents a novel GPR-based magnitude estimation method that integrates multiple seismic wave features and optionally incorporates hypocentral distance information. The method demonstrates superior performance in terms of accuracy, reliability, and generalization ability compared with traditional single-parameter approaches. By effectively reducing estimation errors and mitigating magnitude saturation issues, particularly for larger earthquakes, the proposed GPR method offers significant potential for improving the effectiveness of EEWs across diverse geographical regions. -
引言
北京时间2019年6月17日22点55分四川省宜宾市长宁县发生MS6.0地震，震中位置为（104.90°E，28.34°N），震源深度为16 km，四川、重庆、云南、贵州等多地对此次地震有感。截至6月19日，四川长宁MS6.0地震已造成13人死亡，199人受伤，约10余万人受灾，对当地的社会、生产、生活造成重大影响。据 “地震编目系统” 快报观测报告，截至7月28日，四川地震台网共记录余震约6 888次，其中包含6次M＞4.5的余震（图1，蓝色海滩球）。
![]()
Figure 1. Regional tectonic settings and location of epicenters of 17 June，2019 Changning， Sichuan，earthquake sequence （Deng et al，2002；Tang et al，2018）长宁所处的四川盆地东南缘地区自2018年以来地震活动较为活跃，在此次长宁地震震中位置南侧约15 km处曾发生2018年12月16日四川文兴M5.7和2019年1月3日四川珙县M5.3地震（图1，红色海滩球）。由于四川长宁位于云南、四川与贵州的交会区域，地质构造上处于云贵高原向四川盆地过渡的边缘地带，地质构造背景较为复杂（图1），即长宁形成于青藏高原与四川盆地多期次相互作用的过程中，具有NE向构造，例如华蓥山断裂带，也有NW向规模较小的构造，例如长宁—双河背斜，甚至还有两种构造的叠加。
为了更好地研究四川长宁地震的震源性质和发震构造，本文拟使用中国地震台网中心 “地震编目系统” 快报观测报告记录的震相观测数据，通过双差重定位方法对四川长宁MS6.0地震震后20天内的地震序列空间分布进行分析。除了对地震系列重定位，还将采用W震相反演方法分析中国数字地震台网提供的四川省及周边省级台站所记录的三分量宽频带地震波形资料，获取MS6.0主震及M＞4.5余震的震源机制解，以期为研究长宁MS6.0地震的动力学过程以及长宁地区的地震和地质构造活动提供具有参考价值的地震学证据。
1. 地震序列重定位
1.1 资料及方法
地震序列重定位过程中使用的震相走时资料检索自中国地震台网中心 “地震编目系统” 整理、存储的快报观测报告。观测报告的时间为2019年6月16日22时至2019年7月28日24时，即长宁MS6.0主震之后约42天的时长。我们从 “地震编目系统” 下载的原始震相观测报告包含6 888次余震。为了获取较为可靠的地震序列重定位结果，重定位前需要对下载的震相走时资料按以下条件进行筛选：① 去除震中距大于300 km的到时资料（图2b）；② 每个余震事件需要有5个及以上台站的记录，且每个台站的绝对走时残差在1.5 s之内。经过预处理之后，最终获得6 793次余震的走时资料，其中P波到时数据对10万3 663条，S波到时数据对9万3811条。地震序列重定位中，使用的地震台站总数为27个（图2a），其中包括重庆地震局观测台网的2个固定台站、贵州省地震观测台网的3个固定观测台站、云南省地震局观测台网的2个固定台站及四川省地震局观测台网的21固定台站。从台站分布图中可以看到，重定位中使用的大部分台站位于长宁地震震中西部、北部及南部区域，东部台站覆盖相对较弱（图2a）。
![]()
图 2 （a） 地震序列重定位中所使用的地震台站及长宁MS6.0主震震中（坐标来自于下文的矩张量反演），图中活动断层引自邓起东等 （2002）；（b） P波和S波观测走时曲线Figure 2. （a） Distribution of seismic stations used to relocation and location of the MS6.0 Changning main shock （coordinate from following moment tensor inversion），where dash red lines indicate active faults （Deng et al，2002）； （b） Observed P and S wave travel time curves本文采用双差相对定位方法（Waldhauser，Ellsworth，2000）进行长宁地震序列的重定位。因为该方法可以有效地消除速度模型不准确所引起的误差，且能够产出较好的定位结果，因此近年来在天然地震的重定位研究中得到了广泛的应用（黄浩等，2017；韦伟等，2018；翟亮等，2019）。尽管双差重定位方法可以消除一部分地壳速度模型精度不够引起的地震重定位误差，但是Michelini和Lomax （2004）的研究显示，双差重定位对地壳速度模型的变化还是过于敏感。为了尽可能地避免因地壳速度模型精度不够而引入的重定位误差，我们综合了前人在川滇及周边地区的地震学研究结果（吴建平等，2006；Guo et al，2018）来构建重定位中使用的地壳速度模型（表1）。重定位之前，我们开展了一系列试验，并依据试验结果选择最优控制参数，以此确保重定位过程中最小二乘解的稳定性及地震事件对之间的最优化关联。根据试验结果，重定位中选取地震对成簇参数OBSCT≥6，P波和S波的权重分别为1.0和0.5，余震事件对最大距离为8 km。
表 1 2019年四川长宁地震序列重定位所采用的速度模型Table 1. Crustal velocity model used to relocate the 2019 Changning，Sichuan，earthquake sequence顶层深度/km vP/（km·s−1） vP/vS 0.0 4.58 1.72 4.0 5.65 13.0 6.12 26.0 6.55 32.0 7.32 46.0 8.10 1.2 余震序列重定位结果
通过开展长宁地震序列的双差重定位，我们最终获得了4 056个地震事件的重定位结果，结果显示：东西、南北及深度方向上的平均相对误差分别为0.139 km，0.1 km和0.455 km，走时均方根残差为0.019 s。图3a给出了重定位之后长宁地震序列的空间展布，可以看出：重定位之后地震序列主要沿NW走向呈条带状集中分布；沿震源的深度方向（图3b，c），5—10 km深度范围内地震呈优势分布。图3a显示，经过重新定位之后地震序列的分布呈现明显的分区特征，主震NW方向约4 km处呈现明显的北西与南东余震活动分界线，其中：南东段余震较少，且地震震源的深度较深（约10 km）（图3c）；而北西段地震数量较多，地震分布呈现由浅至深（5—10 km）的连续分布（图3c）。长宁地震序列除了走向上的分区，在震源深度上也呈现明显的分层现象（图3b，c），大部分地震集中分布于5—10 km深度范围，3 km深度以上分布较少。地震序列的深度分布特征，可能揭示了长宁地震震源区域的上地壳结构较脆弱，且深度上存在明显的不均匀性。
![]()
图 3 经重新定位后四川长宁地震序列的平面（a）及深度剖面图（b，c）主震坐标来自于下文的矩张量反演Figure 3. Map view （a） and vertical profiles （b，c） of the relocated Changning，Sichuan，earthquake sequenceThe star indicates the main shock，its coordinate comes from following moment tensor inversion2. 主震及M＞4.5余震震源机制解
为了更深入地了解本次长宁地震的发震机制，我们基于四川及周边西藏、云南、贵州、广西、湖南、湖北、山西、山西、宁夏、青海等省级台站记录到的区域宽频带三分量地震波形资料，采用W震相反演方法获取长宁地震主震及M＞4.5余震的震源机制解。
2.1 方法和数据
矩张量震源机制反演中使用的区域宽频带波形资料来自于郑秀芬等（2009）和国家测震台网数据备份中心（2017）。我们选取震中距处于0°—20°范围内、高信噪比的三分量原始波形资料参加反演。首先，对原始波形资料进行预处理，包括去除仪器响应、去均值、去倾斜，带通滤波，旋转三分量记录得到垂向、径向和切向波形记录；然后，截取P波到时及之后180 s长度时间窗之内的波形数据作为W震相波形资料参加反演。
目前大部分中小地震震源机制反演中所使用的短周期体波或面波资料，容易受到地壳结构不均匀性的影响，因此本研究选取超长周期W震相资料开展震源机制反演。W震相的能量主要集中于100—1 000 s超长周期，以4.5—9.0 km/s （高于S波群速度）在地球内部传播，因为其与众不同的斜坡状波形特征，因此被命名为W震相（Kanamori，1993）。因为超长周期，W震相主要集中在上地幔传播，较少受到大陆地壳浅层强烈各向异性速度结构的影响；此外W震相的传播速度较快，可以用来快速可靠地确定地震的震源参数（Kanamori，Rivera，2008；Duputel et al，2012）。近年来基于W震相的矩张量震源机制反演方法已经在国内外的震源机制研究中得到广泛的应用（郭志等，2017；韦伟等，2018），且研究结果与其它方法获取的结果显示了较好的一致性（Duputel et al，2012）。
目前地震数据处理中通常采用原始波形资料反卷积仪器响应信息的方式去除仪器响应，但是对于具有超长周期特性的W震相资料，采用上述方法去除仪器响应得到的原始波形资料并不准确。参考Kanamori和Rivera （2008）的研究结果，我们采用时间域递归滤波器来去除仪器响应，该方法最重要的过程为寻找与地震仪器零点、极点及增益信息相匹配的二阶微分方程的常系数（Zhu，2003）。在此过程中，在要求的频率范围之内一些地震台站可能无法找到合适的递归滤波器参数，对于此类地震台所记录的数据，在预处理过程中直接舍弃。
地震仪所观测到的地震波形图的变化特征也会受到震源特性及地球介质的影响，数值计算可以模拟这些效应进行理论地震图的合成。理论地震图合成中一个主要组成元素为理论格林函数，理论格林函数主要包含地球介质对脉冲信号的响应信息。对于区域短周期体波、面波或全波形格林函数，通常采用基于矩阵传播的方式进行计算（Zhu，Rivera，2002），且计算过程中无需考虑地球自身重力对理论格林函数的影响。但是对于超长周期的W震相，地球自身重力场对地震波形特征的影响不能忽略，因此本研究选择基于简振正型叠加方法的Mineos软件包（Masters et al，2011）来构建理论格林函数库。对于点源模型，震源特性通常可用9个矩张量来刻画，而且因为地震矩张量的对称性，可以进一步减少到仅使用6个独立的矩张量来完全刻画震源（Jost，Herrmann，1989）。在震源机制反演过程中，利用上述理论格林函数与矩张量的加权线性叠加计算得到理论地震图，之后通过理论地震图与实际观测地震波形资料的比对，找出一组使得理论地震图与实际观测资料最佳拟合的矩张量参数来得到震源机制解。
2.2 2019年6月17日四川长宁MS6.0地震震源机制解
为了获取最优震源机制解，在反演中需要对原始波形资料进行多次质量控制，开展震中位置的空间网格搜索。波形反演分为两步：第一步，使用中国地震局（2019）发布的长宁地震的初始震源参数作为参考，进行数次反演，每次反演完成后，去除波形拟合均方差较大台站的数据，这样最终共获取227个台站的414个分量的波形数据用于空间网格搜索反演；第二步，利用初步反演筛选得到的观测数据，对震源区域进行空间网格划分，并进行空间网格搜索，获取最优震源参数，包括震源的三维空间位置、地震矩张量等。
通过空间网格搜索反演获取的最优地震矩张量解如图4a所示。结果显示：2019年6月17日四川长宁MS6.0地震的标量地震矩为M0＝5.18×1017 N·m，折合矩震级MW5.74，最优矩心深度为7.5 km；六个地震矩张量Mxx，Myy，Mzz，Mxy，Myz，Mxz分别为0.334 7×1018，0.196 0×1018，−0.530 7×1018，0.094 9×1018，−0.071 0×1018，0.294 4×1018 N·m；两个发震断层节面解分别为节面Ⅰ ，走向12°，倾角50°，滑动角139°，节面Ⅱ ，走向131°，倾角59°，滑动角48°。
![]()
图 4 （a） 2019年6月17日四川长宁MS6.0地震的矩张量反演结果；（b） 部分参加反演台站的波形拟合及台站分布图，台站名称标示于波形图上方Figure 4. （a） Centroid moment tensor solution for the MS6.0 Changning，Sichuan，earthquake on 17 June 2019；（b） Comparison of the observed waveforms （black lines） and synthetic ones （red lines） for moment tensor solution，where the station name is marked above each waveform部分参加反演台站实际观测波形与理论波形的对比如图4b所示，可见实际观测资料与理论地震图拟合得较好。波形对比图右侧给出了反演使用的地震台站（橙色圆点）的空间分布、当前波形所对应台站位置（红色圆点）及震中位置（蓝色六角星）。从台站分布图（图4b）可以看出，大部分台站位于震中所处位置的东部、北部及南部，西部台站分布相对较少。总体而言，可用台站的空间分布为反演提供了较为均匀的方位角覆盖，为获取可靠的反演结果提供了坚实的数据基础。
空间网格搜索的反演过程中，深度网格搜索步长设为2.0 km，初始搜索深度设为3.5 km，最大搜索深度设为15.5 km，共7个深度位置。图5a给出了波形拟合均方差随深度的变化情况，图中显示长宁地震的最佳矩心深度为7.5 km。图5b显示7.5 km深度的平面上，波形拟合均方差随空间位置的变化情况（圆点直径及颜色），图中 “＋” 标示二维空间网格搜索的最优震中位置，其坐标为（104.9°E，28.34°N）。这样看来，通过空间网格搜索获取的震源深度与中国地震局（2019）发布的震源深度（16 km）存在明显差异，而震中位置（104.9°E，28.34°N）与中国地震局（2019）发布的震中位置一致。
![]()
图 5 2019年6月17日四川长宁MS6.0地震震源深度及震中位置空间网格搜索结果（a） 深度搜索与波形拟合均方差变化图；（b） 经纬度搜索与波形拟合均方差分布图，图中黑色十字标示最佳震中位置Figure 5. Focal depth and grid search results of optimal centroid location for 17 June 2019 Changning earthquake（a） Variations of waveform fitting root mean square （RMS） with depth；（b） Spatial variation of waveform fitting RMS，where best-fitting location is marked with a black cross2019年6月17日长宁地震发生之后，国内外多家机构发布了本次地震的震源参数信息，列于表2。从表2中可看出，本研究获取的震源机制与中国科学院地质与地球物理研究所（Institute of Geology and Geophysics，Chinese Academy of Sciences，缩写为IGGCAS）发布的结果比较相近；中国地震台网中心（China Earthquake Networks Center，缩写为CENC）、美国地质调查局（United States Geological Survey，缩写为USGS）、哈佛大学全球矩张量（Global Centroid Moment Tensor，缩写为GCMT）和中国地震局地球物理研究所（Institute of Geophysics，China Earthquake Administration，缩写为IGP-CEA）的结果比较相近，发震断层的性质也比较接近，逆断层为主，外加少量的走滑分量。中国地震局地震预测研究所（Institute of Earthquake Forecasting，China Earthquake Administration，缩写为IEF-CEA）的结果与上述结果存在一定差异，其结果显示发震断层性质以正走滑为主。
表 2 国内外相关机构发布的2019年6月17日四川长宁MS6.0地震的震源机制参数Table 2. The focal mechanism parameters for the MS6.0 Changning，Sichuan，earthquake on 17 June 2019 released by related institutions机构 节面Ⅰ 节面Ⅱ 震源
深度
/kmMW 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 美国地质调查局（USGS） 308 45 40 187 63 127 11.5 5.79 哈佛大学全球矩张量（GCMT） 323 57 65 184 40 123 12.0 5.7 中国地震台网中心（CENC） 350 67 93 162 23 82 16.0 6.0 中国科学院地质与地球物理研究所（IGGCAS） 119 58 9 24 82 147 5.0 5.8 中国地震局地球物理研究所（IGP-CEA） 307 58 40 191 57 141 16.0 6.0 中国地震局地震预测研究所（IEF-CEA） 296 81 −13 28 77 −170 19.0 5.8 对于同一个地震事件，不同的研究机构给出的震源机制结果存在明显差异，这源于以下两方面。一方面，差异来源于所采用的反演方法和观测资料不同。例如本研究、CENC和USGS的震源参数均是采用W震相反演方法（Kanamori，Rivera，2008）获取，但是CENC和本研究主要使用省级台站记录的区域波形资料，而USGS主要使用的是远场波形资料。此外，本研究的结果经过深度空间搜索优化。由于所使用波形资料及深度空间搜索优化的差异，导致使用同一方法而最终结果不同。GCMT的结果主要使用长周期体波及面波资料（Ekström et al，2012）反演获取，IGP-CEA的结果主要基于CAP （cut-and-paste）方法（Zhu，Helmberger，1996）反演区域波形资料获取，IGGCAS和IEF-CEA 的结果主要使用区域全波形资料反演获取，但由于反演方法不同（郝金来，姚振兴，2012；Dreger，Helmberger，1993），所以导致震源参数存在明显差异。另外，对于区域体波资料的反演，计算格林函数时使用的地壳速度结构模型不同，也可能会对最终反演结果产生一定的影响。另一方面，震源参数的差异可能与震源的复杂性有关，而长宁地震震源是否具有复杂性及其对震源机制的影响，尚需进一步深入研究。
2.3 M＞4.5余震的震源机制
除长宁地震序列主震的震源机制之外，我们还从 “数据备份中心” 下载了M＞4.5共6次余震的区域波形资料，并反演获取其震源参数，如表3所示。可以看出，大部分余震均分布在约7—10 km的深度范围内，而发震断层的性质主要以逆断为主，外加少量的走滑分量，其发震机制与主震比较接近（图1）。
表 3 四川长宁地震序列六次M＞4.5余震的震源参数Table 3. Focal parameters for six M＞4.5 aftershocks of the Changning earthquake sequence发震时刻 节面Ⅰ 节面Ⅱ 震源
深度
/kmMW 年−月−日 时:分:秒 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 2019−06−17 23:36:01 175 51 117 316 46 60 9.5 5.08 2019−06−18 07:34:33 156 42 118 300 53 66 7.5 4.72 2019−06−22 22:29:56 162 44 75 3 47 104 9.5 5.19 2019−06−23 08:28:17 146 59 20 45 72 147 7.5 4.44 2019−07−03 12:26:53 135 51 93 309 38 85 7.5 4.61 2019−07−04 10:17:58 192 43 82 22 46 96 9.5 5.16 3. 讨论与结论
本研究采用双差定位方法分析四川、云南、重庆各省地震局区域台网提供的具有相对较好方位角覆盖的震相走时观测资料，获取了四川长宁MS6.0强震序列的重定位结果，重定位结果在东西、南北方向和垂向的精度分别为0.063 km，0.265 km和0.434 km。重定位之后地震的空间分布特征更加清晰地展示了长宁地震序列主要沿NW方向呈条带状扩展，以主震为起点，地震序列沿着NW方向展布约23 km；地震序列的优势分布深度为5—10 km，主震的震源深度约6.9 km，余震向浅部及深部双向扩展；地震序列在深度空间上接近垂直分布，并随深度增加呈轻微NE向倾斜趋势，揭示发震断层面可能较为陡峭。此外，地震序列的空间展布在主震NW向约4 km处存在明显的分区特征，在约3 km深度处存在明显的深度分层特征，这可能揭示了长宁地震震中及附近区域的上地壳结构更脆更弱，且深度上存在显著的不均匀性。沿NW走向的地震序列的深度分布显示，在主震NW方向从地表到约11 km深度存在一个上宽下窄的地震聚集区，且震级较大的余震几乎均集中在该区域，我们认为该区域属于主震发生时地震破裂滑动位移较小的区域，在主震破裂的过程中该区域原始积累的应力未得到充分释放，震后受到主震破裂引起的应力变化影响而以余震发生的方式逐步被释放。
采用W震相方法分析区域波形资料获取的主震及M＞4.5余震的震源机制解表明，此次地震为逆断为主兼具少量走滑的地震破裂事件，主震的最优矩心深度为7.5 km，矩震级为MW5.74。综合分析主震、余震的震源机制和地震序列的空间展布特征以及震中附近区域地质构造背景（唐永等，2018），推测本次地震的发震构造为NW走向长宁—双河背斜，也就是本研究获取震源参数中的节面Ⅱ为发震断层，其震源参数为走向131°，倾角59°，滑动角48°。
本研究通过对经重定位的2019年四川长宁地震的余震序列进行反演所得的主震及部分余震的震源机制表明，此次长宁地震序列在空间上表现为沿长宁—双河背斜核部及北部区域集中分布。长宁—双河背斜为四川盆地低缓褶皱带向云贵高原的过渡带，地质上表现为多方向多期次的构造变形特征。长宁—双河背斜的东侧主要受到湘西华南地块的挤压应力作用，西侧则受到青藏高原内部物质向南挤出的应力作用；西端以华蓥山断裂带为界，南部叠加昭通—鲁甸断裂带构造转换作用导致的挤压、抬升作用，最终形成现今的背斜构造形迹（唐永等，2018）。长宁—双河背斜总体呈现NW−SE走向，空间展布长约70 km，背斜东南部较宽，而西北部则逐渐收窄，且向WS方向发生弯曲（图1）。何登发等（2019）的地震反射剖面研究结果表明，长宁—双河背斜在地质构造上表现为断层转折褶皱背斜，核部主要发育一系列逆冲断层，背斜西南翼的地层较为平缓，而东北翼的地层较为陡峭。经过重定位的余震序列平面展布表现为沿长宁—双河背斜的东北翼及接近背斜核部区域集中分布，余震优势分布方向大致平行于背斜走向（图3a），余震序列的深度分布特征则表现为浅部近垂直于地表分布，深部呈NE向倾斜（图3b）。余震序列的空间分布特征与长宁—双河背斜东北翼的地质构造呈现较高的相关性，印证了本文余震序列重定位结果的可靠性。此外，主震及几次震级较大余震的震源机制结果表明，发震断层以逆冲为主，该结果与长宁—双河背斜的地质构造及应力背景较为一致。就在长宁—双河背斜的西南部分别于2018年底和2019年初发生过两次M5.0左右地震，本文结果显示余震序列在深度上呈分层特征，余震优势分布深度约为5—10 km，这与何登发等（2019）对这两次地震及余震的研究结果较为一致。
地震序列重定位中使用的震相走时数据来自于 “地震编目系统” 正式观测报告，区域波形数据来自于中国地震局地球物理研究所国家测震台网数据备份中心（doi：10.11998/SeisDmc/SN），W震相反演软件包来自于法国斯特拉斯堡大学（http://wphase.unistra.fr），文中图件使用GMT （Wessel， Smith，1991）和Matplotlib （Hunter，2007）软件包绘制。
-
![]()
图 1 强震动记录随震级和震源距的分布（每个点代表一条地震动记录）
Figure 1. Distribution of strong motion records with magnitude and hypocentral distance （each point represents a ground motion record）
![]()
图 2 GPR的网络结构示意图
x为输入，K（${x^{i}}\text{，} x^{j} $）为协方差函数，y为输出
Figure 2. Schematic diagram of the GPR network structure
x is the input，K（${x^{i}}\text{，} x^{j} $） is the covariance function，and y is the output
![]()
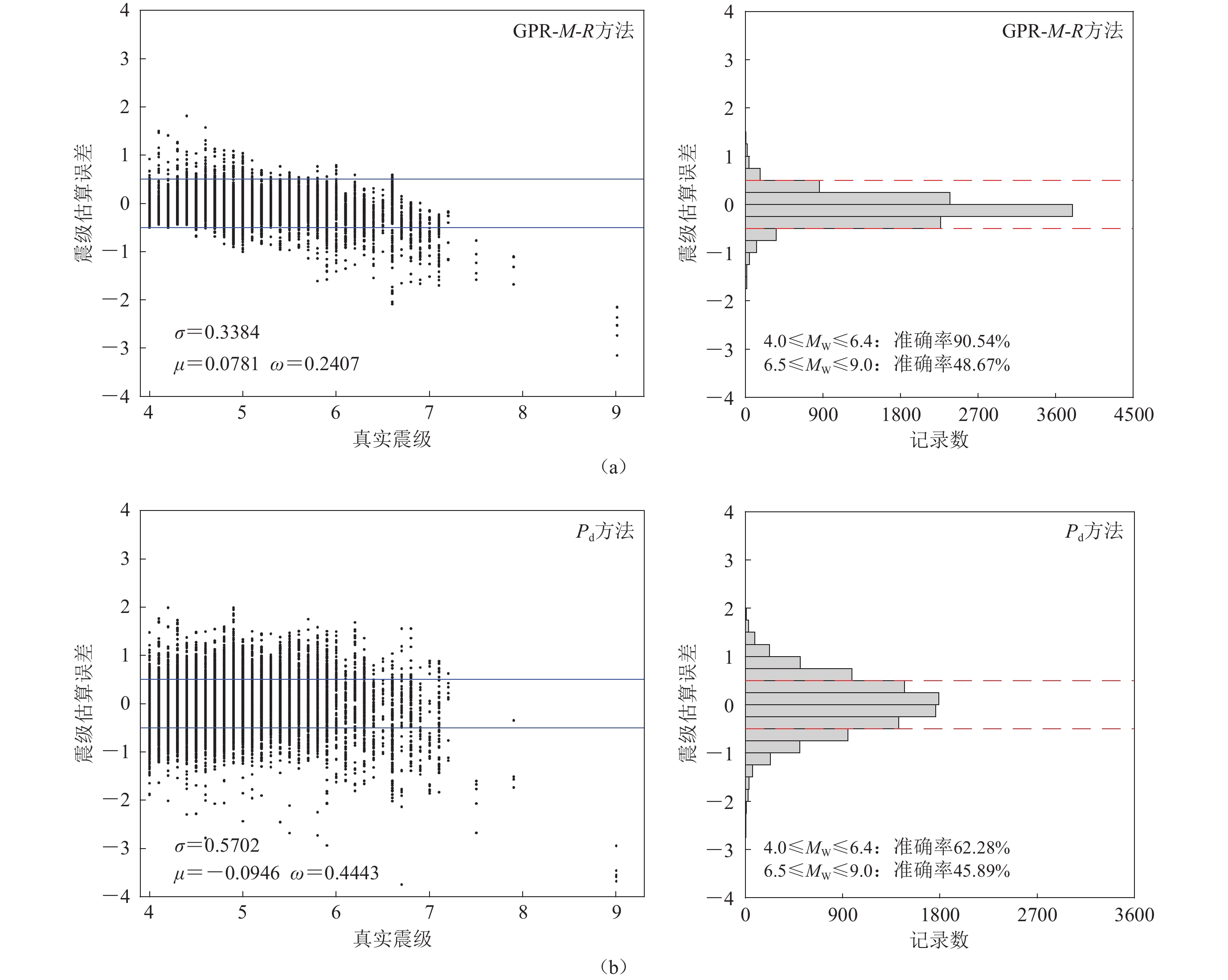
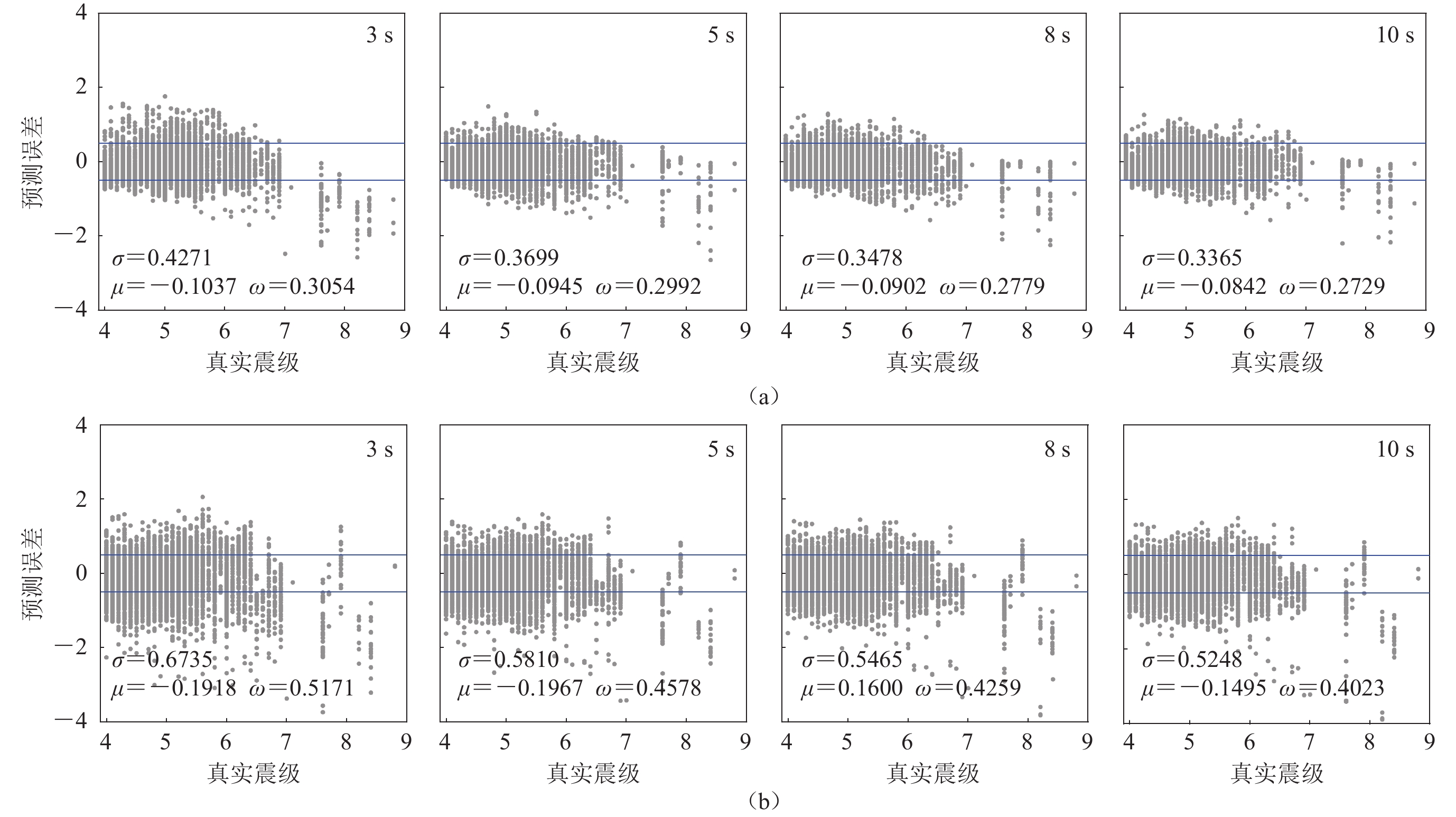
图 3 初至3 s P波时GPR-M （a）和$ {\tau ^{\max }_{\mathrm{p}}}$（b）估算震级的误差分布及其直方图
图中的散点表示每条记录估算震级的误差，蓝色实线和红色虚线表示±0.5，σ为误差标准差，μ为误差均值，ω为误差绝对值均值，准确率定义为误差在$ ［ $−0.5， 0.5$ ］ $的记录数与记录总数的比值，下同
Figure 3. Distribution of estimated magnitude errors by GPR-M （a） and $ {\tau ^{\max }_{\mathrm{p}}}$ （b） at initial 3 s P-wave
Scatter points show magnitude estimation errors based on per record. Blue solid lines and red dashed lines indicate ±0.5 . σ is error standard deviation，μ is mean error，ω is mean absolute error，accuracy is the ratio of records with errors in $ ［ $−0.5，0.5$ ］ $ to total records，the same below
![]()
图 4 初至3 s P波GPR-M-R （a）和P d （b）方法估算震级的误差分布
Figure 4. Distributions and histograms of estimated magnitude errors for GPR-M-R （a） and P d （b） for initial 3 s P-wave
![]()
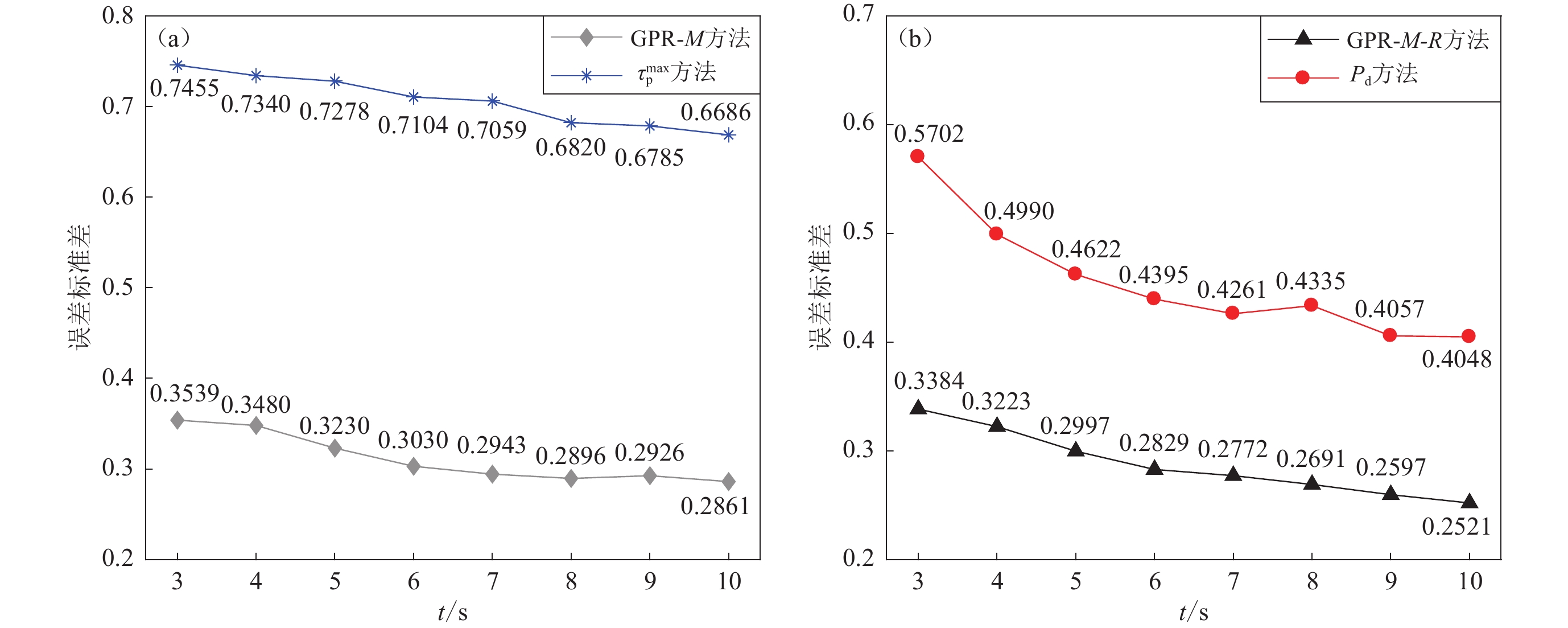
图 5 初至3—10 s地震波的不同方法估算震级的误差标准差对比
（a） GPR-M与$ {\tau ^{\max }_{\mathrm{p}}}$方法对比；（b） GPR-M与P d方法对比
Figure 5. Comparison of the standard deviation of errors in estimating magnitudes for initial 3−10 s seismic waves
（a） Comparison of GPR-M method with $ {\tau ^{\max }_{\mathrm{p}}}$ method ；（b） Comparison of GPR-M method with P d method
![]()
图 6 初至3—10 s地震波的GPR-M方法和$ {\tau ^{\max }_{\mathrm{p}}}$方法估算不同范围震级的准确率随时间变化趋势的对比
Figure 6. Comparison of the trends in estimation accuracy of different magnitude ranges based on the GPR-M and $ {\tau ^{\max }_{\mathrm{p}}}$ methods using initial 3−10 s seismic waves
（a） 4.0≤MW≤6.4；（b） 6.5≤MW≤9.0
![]()
图 7 初至3—10 s地震波的GPR-M-R方法和P d方法估算不同范围震级的准确率随时间变化趋势的对比
Figure 7. Comparison of the trend of magnitude estimation accuracy change over time by the GPR-M-R and P d methods using initial 3−10 s seismic waves
（a） 4.0≤MW≤6.4；（b） 6.5≤MW≤9.0
![]()
图 8 P波到达后3 s，5 s，8 s，10 s GPR-M （a）和$ {\tau ^{\max }_{\mathrm{p}}}$ （b）方法估算泛化数据集震级的误差分布
Figure 8. Distributions of estimated magnitude errors in the generalized dataset using the GPR-M （a） and $ {\tau ^{\max }_{\mathrm{p}}}$ （b） at the P-wave first arrival times of 3 s，5 s，8 s，and 10 s
![]()
图 9 P波到达后3 s，5 s，8 s，10 s GPR-M-R （a）和P d （b）估算泛化数据集震级的误差分布
Figure 9. Distributions of estimating magnitude errors in the generalized dataset using the GPR-M （a） and P d （b） at the P-wave arrival times of 3 s，5 s，8 s，and 10 s
![]()
图 10 用于检验GPR震级估算效果所选取的我国三次地震的震中及所用台站分布
Figure 10. Distribution of epicenters and the stations used for testing the effectiveness of GPR magnitude estimation for three earthquakes in China
![]()
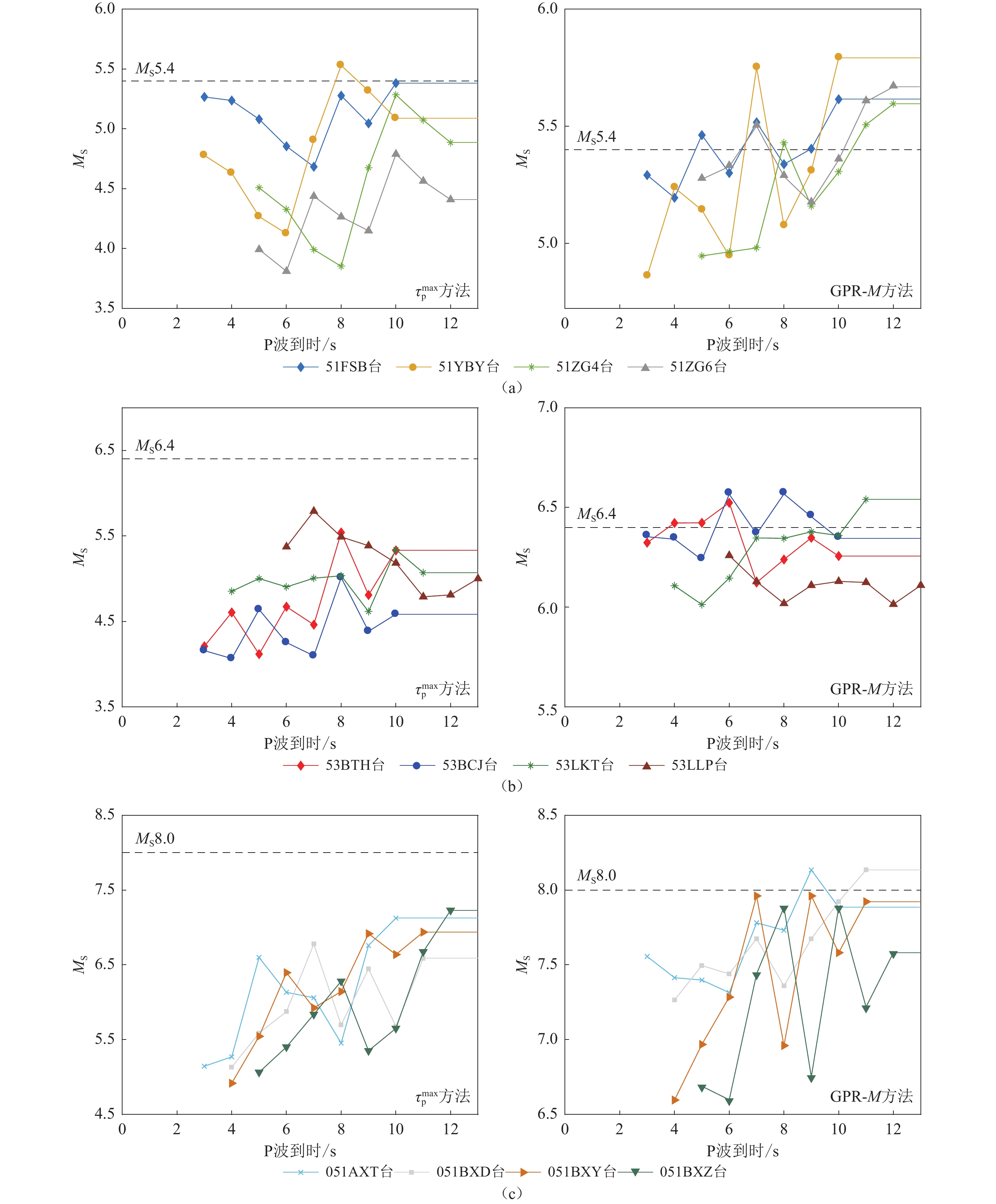
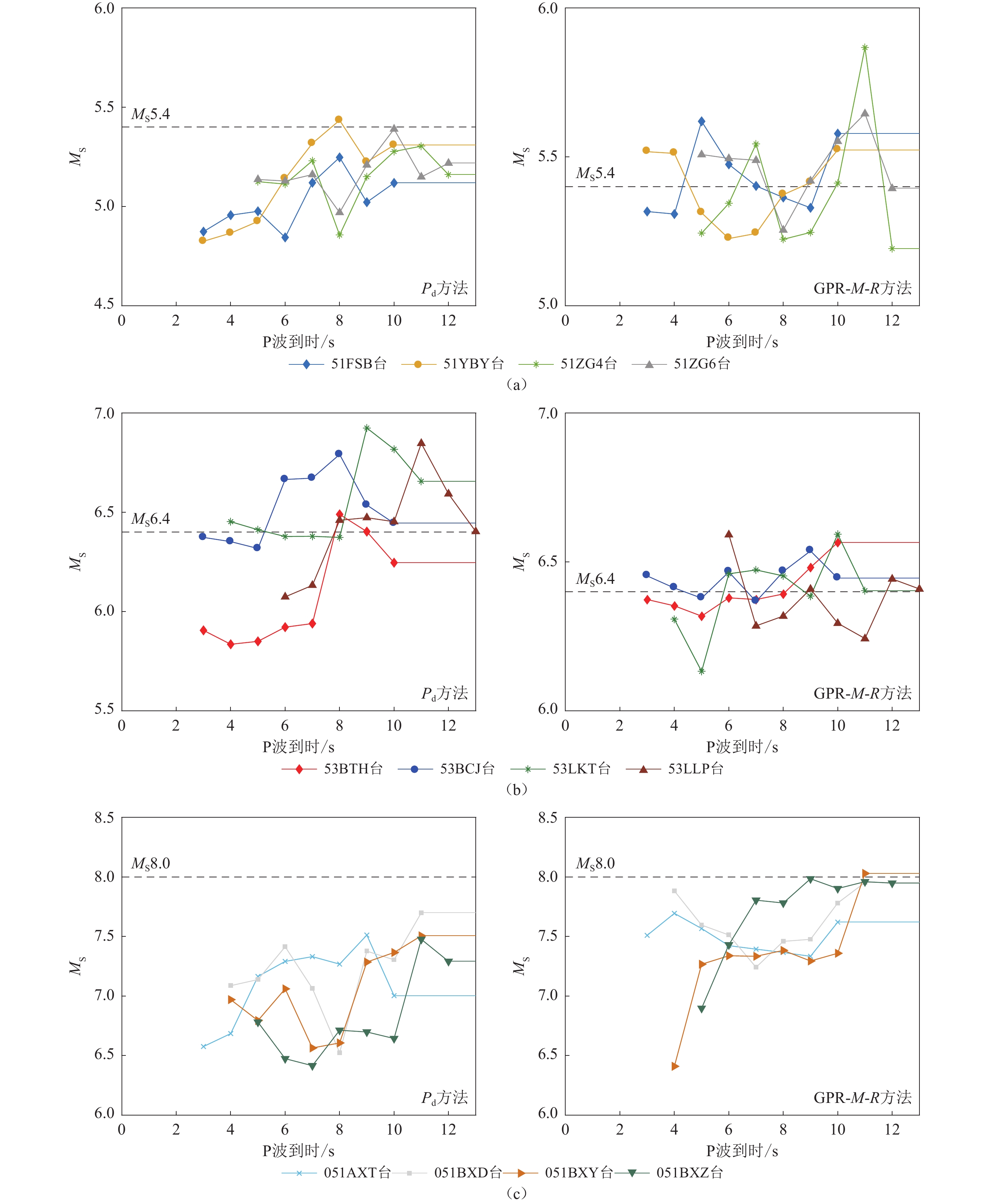
图 11 使用GPR-M方法（左）和$ {\tau ^{\max }_{\mathrm{p}}}$方法（右）持续估算我国2019年宜宾MS5.4 （a）、2021年漾濞MS6.4 （b）和2008年汶川MS8.0 （c）地震震级的结果
Figure 11. Results of continuous magnitude estimation for the 2019 Yibin MS5.4 （a），2021 Yangbi MS6.4 （b），and 2008 Wenchuan MS8.0 （c） earthquakes using the GPR-M-R （left panels） and $ {\tau ^{\max }_{\mathrm{p}}}$ （right panels） methods
![]()
图 12 使用GPR-M-R （左）和P d （右）方法持续估算我国2019年宜宾MS5.4 （a）、2021年漾濞MS6.4 （b）和2008年汶川MS8.0 （c）地震震级的结果
Figure 12. Results of continuous magnitude estimation for the 2019 Yibin MS5.4 （a），2021 Yangbi MS6.4 （b），and 2008 Wenchuan MS8.0 （c） earthquakes using the GPR-M-R （left panels） and P d （right panels） methods
表 1 初至3—10 s地震波的Pd和$ {\tau ^{\max }_{\mathrm{p}}} $方法的拟合系数表
Table 1 Fitting coefficients for the Pd and $ {\tau ^{\max }_{\mathrm{p}}} $ methods based on the first 3−10 s seismic waves
初至地震波
窗长/s$P_{{\mathrm{d}}} $方法 $ {\tau ^{\max }_{\mathrm{p}}}$方法 a b c a b 3 0.639 4 −3.987 2 −0.840 7 0.309 6 −2.049 4 4 0.681 4 −3.910 9 −0.966 4 0.320 6 −2.048 3 5 0.708 0 −3.740 4 −1.104 4 0.329 8 −2.041 8 6 0.723 6 −3.518 2 −1.248 1 0.339 8 −2.016 5 7 0.738 2 −3.292 8 −1.378 0 0.348 6 −1.975 3 8 0.740 9 −3.070 7 −1.478 3 0.352 6 −1.955 5 9 0.737 8 −2.897 5 −1.538 8 0.358 3 −1.911 7 10 0.733 4 −2.791 4 −1.561 7 0.364 7 −1.875 0 
下载: 导出CSV
-
郭凯,温瑞智,杨大克,彭克银. 2016. 地震预警系统的效能评估和社会效益分析[J]. 地震学报,38(1):146–154. doi: 10.11939/jass.2016.01.015 Guo K,Wen R Z,Yang D K,Peng K Y. 2016. Effectiveness evaluation and social benefits analyses on earthquake early warning system[J]. Acta Seismologica Sinica,38(1):146–154 (in Chinese).
何志昆,刘光斌,赵曦晶,王明昊. 2013. 高斯过程回归方法综述[J]. 控制与决策,28(8):1121–1129. He Z K,Liu G B,Zhao X J,Wang M H. 2013. Overview of Gaussian process regression[J]. Control and Decision,28(8):1121–1129 (in Chinese).
金星,张红才,李军,韦永祥,马强. 2012. 地震预警震级确定方法研究[J]. 地震学报,34(5):593–610. doi: 10.3969/j.issn.0253-3782.2012.05.002 Jin X,Zhang H C,Li J,Wei Y X,Ma Q. 2012. Research on earthquake early warning magnitude estimate[J]. Acta Seismologica Sinica,34(5):593–610 (in Chinese).
林彬华,金星,康兰池,韦永祥,李军,张燕明,陈惠芳,周施文. 2021. 基于卷积神经网络的地震震级测定研究[J]. 地球物理学报,64(10):3600–3611. doi: 10.6038/cjg2021O0370 Lin B H,Jin X,Kang L C,Wei Y X,Li J,Zhang Y M,Chen H F,Zhou S W. 2021. The research of earthquake magnitude determination based on convolutional neural networks[J]. Chinese Journal of Geophysics,64(10):3600–3611 (in Chinese).
马美帅,王延伟,汪祚赚,赵庆旭,潘代洪. 2022. 基于累积绝对位移值的震级估算方法[J]. 自然灾害学报,31(2):93–101. Ma M S,Wang Y W,Wang Z Z,Zhao Q X,Pan D H. 2022. Magnitude estimation based on the cumulative absolute displacement[J]. Journal of Natural Disasters,31(2):93–101 (in Chinese).
孙斌,姚海涛,刘婷. 2012. 基于高斯过程回归的短期风速预测[J]. 中国电机工程学报,32(29):104–109. Sun B,Yao H T,Liu T. 2012. Short-term wind speed forecasting based on Gaussian process regression model[J]. Proceedings of the CSEE,32(29):104–109 (in Chinese).
王延伟,李小军,曹振中,兰景岩,刘娟. 2020. 基于KiK-net井下基岩强震动记录的持续地震预警震级估算方法[J]. 地震工程与工程振动,40(4):42–52. Wang Y W,Li X J,Cao Z Z,Lan J Y,Liu J. 2020. Continuous estimation magnitude for earthquake early warning based on KiK-net borehole bedrock strong motions[J]. Earthquake Engineering and Engineering Dynamics,40(4):42–52 (in Chinese).
位栋梁,王延伟,王自法,廖吉安,赵登科. 2022. 基于卷积神经网络的地震震级快速估算方法[J]. 地震学报,44(2):316–326. doi: 10.11939/jass.20210198 Wei D L,Wang Y W,Wang Z F,Liao J A,Zhao D K. 2022. A fast estimation method of earthquake magnitude based on convolutional neural networks[J]. Acta Seismologica Sinica,44(2):316–326 (in Chinese).
杨黎薇,林国良,邱志刚,江汶乡,王玉石. 2018. 基于人工神经元网络和多特征参数的预警震级估算[J]. 地震研究,41(2):302–310. doi: 10.3969/j.issn.1000-0666.2018.02.019 Yang L W,Lin G L,Qiu Z G,Jiang W X,Wang Y S. 2018. Study on magnitude estimation of earthquake early warning based on various characteristic parameters and artificial neural networks[J]. Journal of Seismological Research,41(2):302–310 (in Chinese).
朱景宝,宋晋东,李山有. 2021. 基于支持向量机的地震预警震级快速估算研究[J]. 振动与冲击,40(7):126–134. Zhu J B,Song J D,Li S Y. 2021. Rapid magnitude estimation for earthquake early warning based on SVM[J]. Journal of Vibration and Shock,40(7):126–134 (in Chinese).
Alcik H,Ozel O,Apaydin N,Erdik M. 2009. A study on warning algorithms for Istanbul earthquake early warning system[J]. Geophys Res Lett,36(5):L00B05.
Allen R M,Kanamori H. 2003. The potential for earthquake early warning in southern California[J]. Science,300(5620):786–789. doi: 10.1126/science.1080912
Böse M,Heaton T,Hauksson E. 2012. Rapid estimation of earthquake source and ground-motion parameters for earthquake early warning using data from a single three-component broadband or strong-motion sensor[J]. Bull Seismol Soc Am,102(2):738–750. doi: 10.1785/0120110152
Cheng M H,Wu S,Heaton T H,Beck J L. 2014. Earthquake early warning application to buildings[J]. Eng Struct,60:155–164. doi: 10.1016/j.engstruct.2013.12.033
Chung A I,Henson I,Allen R M. 2019. Optimizing earthquake early warning performance:ElarmS-3[J]. Seismol Res Lett,90(2A):727–743. doi: 10.1785/0220180192
Cua G,Fischer M,Heaton T,Wiemer S. 2009. Real-time performance of the virtual seismologist earthquake early warning algorithm in southern California[J]. Seismol Res Lett,80(5):740–747. doi: 10.1785/gssrl.80.5.740
Cuéllar A,Suárez G,Espinosa-Aranda J M. 2018. A fast earthquake early warning algorithm based on the first 3 s of the P-wave coda[J]. Bull Seismol Soc Am,108(4):2068–2079. doi: 10.1785/0120180079
Festa G,Zollo A,Lancieri M. 2008. Earthquake magnitude estimation from early radiated energy[J]. Geophys Res Lett,35(22):L22307.
Hsiao N C,Wu Y M,Shin T C,Zhao L,Teng T L. 2009. Development of earthquake early warning system in Taiwan[J]. Geophys Res Lett,36(5):L00B02.
Hsiao N C,Wu Y M,Zhao L,Chen D Y,Huang W T,Kuo K H,Shin T C,Leu P L. 2011. A new prototype system for earthquake early warning in Taiwan[J]. Soil Dyn Earthq Eng,31(2):201–208. doi: 10.1016/j.soildyn.2010.01.008
Hsu T Y,Huang S K,Chang Y W,Kuo C H,Lin C M,Chang T M,Wen K L,Loh C H. 2013. Rapid on-site peak ground acceleration estimation based on support vector regression and P-wave features in Taiwan[J]. Soil Dyn Earthq Eng,49:210–217. doi: 10.1016/j.soildyn.2013.03.001
Hua T,Li Q Y,Dai K R,Zhang X J,Zhang H. 2023. Image denoisingvia neighborhood-based multidimensional Gaussian process regression[J]. Signal Image Video P, 17 (2):389-397.
Ide S. 2019. Frequent observations of identical onsets of large and small earthquakes[J]. Nature,573(7772):112–116. doi: 10.1038/s41586-019-1508-5
Kamigaichi O,Saito M,Doi K,Matsumori T,Tsukada S,Takeda K,Shimoyama T,Nakamura K,Kiyomoto M,Watanabe Y. 2009. Earthquake early warning in Japan:Warning the general public and future prospects[J]. Seismol Res Lett,80(5):717–726. doi: 10.1785/gssrl.80.5.717
Kanamori H. 2005. Real-time seismology and earthquake damage mitigation[J]. Annu Rev Earth Planet Sci,33(1):195–214. doi: 10.1146/annurev.earth.33.092203.122626
Kohler M D,Smith D E,Andrews J,Chung A I,Hartog R,Henson I,Given D D,De Groot R,Guiwits S. 2020. Earthquake early warning ShakeAlert 2.0:Public rollout[J]. Seismol Res Lett,91(3):1763–1775. doi: 10.1785/0220190245
Leyton F,Ruiz S,Baez J C,Meneses G,Madariaga R. 2018. How fast can we reliably estimate the magnitude of subduction earthquakes?[J]. Geophys Res Lett,45(18):9633–9641. doi: 10.1029/2018GL078991
Li Z F,Meier M A,Hauksson E,Zhan Z W,Andrews J. 2018. Machine learning seismic wave discrimination:Application to earthquake early warning[J]. Geophys Res Lett,45(10):4773–4779. doi: 10.1029/2018GL077870
Mousavi S M,Beroza G C. 2020. A machine-learning approach for earthquake magnitude estimation[J]. Geophys Res Lett,47(1):e2019GL085976. doi: 10.1029/2019GL085976
Nakamura Y. 1988. On the urgent earthquake detection and alarm system (UrEDAS)[C]//Proceedings of 9th World Conference on Earthquake Engineering. Tokyo:International Association for Earthquake Engineering:673−678.
Nazeri S,Shomali Z H,Colombelli S,Elia L,Zollo A. 2017. Magnitude estimation based on integrated amplitude and frequency content of the initial P wave in earthquake early warning applied to Tehran,Iran[J]. Bull Seismol Soc Am,107(3):1432–1438. doi: 10.1785/0120160380
Nguyen-Tuong D,Peters J,Seeger M. 2008. Local Gaussian process regression for real time online model learning and control[C]//Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver,Canada:Curran Associates Inc:1193−1200.
Olson E L,Allen R M. 2005. The deterministic nature of earthquake rupture[J]. Nature,438(7065):212–215. doi: 10.1038/nature04214
Park C,Huang J Z,Ding Y. 2011. Domain decomposition approach for fast Gaussian process regression of large spatial data sets[J]. J Mach Learn Res,12:1697–1728.
Peng C Y,Yang J S,Zheng Y,Zhu X Y,Xu Z Q,Chen Y. 2017. New τc regression relationship derived from all P wave time windows for rapid magnitude estimation[J]. Geophys Res Lett,44(4):1724–1731. doi: 10.1002/2016GL071672
Perol T,Gharbi M,Denolle M. 2018. Convolutional neural network for earthquake detection and location[J]. Sci Adv,4(2):e1700578. doi: 10.1126/sciadv.1700578
Rasmussen C E,Williams C K I. 2006. Gaussian Processes for Machine Learning[M]. Cambridge:MIT Press:7−32.
Rohani A,Taki M,Abdollahpour M. 2018. A novel soft computing model (Gaussian process regression with K-fold cross validation) for daily and monthly solar radiation forecasting (Part:I)[J]. Renew Energy,115:411–422. doi: 10.1016/j.renene.2017.08.061
Seeger M. 2004. Gaussian processes for machine learning[J]. Int J Neural Syst,14(2):69–106. doi: 10.1142/S0129065704001899
Shieh J T,Wu Y M,Allen R M. 2008. A comparison of τc and τpmax for magnitude estimation in earthquake early warning[J]. Geophys Res Lett,35(20):L20301.
Wang Y W,Li X J,Wang Z F,Shi J P,Bao E H. 2021. Deep learning for P-wave arrival picking in earthquake early warning[J]. Earthq Eng Eng Vib,20(2):391–402. doi: 10.1007/s11803-021-2027-6
Wang Y W,Li X J,Li L,Wang Z F,Lan J Y. 2022. New magnitude proxy for earthquake early warning based on initial time series and frequency[J]. Seismol Res Lett,93(1):216–225. doi: 10.1785/0220210106
Wang Y W,Li X J,Wang Z F,Liu J. 2023. Deep learning for magnitude prediction in earthquake early warning[J]. Gondwana Res,123:164–173. doi: 10.1016/j.gr.2022.06.009
Wu Y M. 2002. A virtual subnetwork approach to earthquake early warning[J]. Bull Seismol Soc Am,92(5):2008–2018. doi: 10.1785/0120010217
Wu Y M,Kanamori H. 2005. Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves[J]. Bull Seismol Soc Am,95(3):1181–1185. doi: 10.1785/0120040193
Wu Y M,Zhao L. 2006. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning[J]. Geophys Res Lett,33(16):L16312.
Zhang H C,Jin X,Wei Y X,Li J,Kang L C,Wang S C,Huang L Z,Yu P Q. 2016. An earthquake early warning system in Fujian,China[J]. Bull Seismol Soc Am,106(2):755–765. doi: 10.1785/0120150143
Ziv A. 2014. New frequency-based real-time magnitude proxy for earthquake early warning[J]. Geophys Res Lett,41(20):7035–7040. doi: 10.1002/2014GL061564
Zollo A,Lancieri M,Nielsen S. 2006. Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records[J]. Geophys Res Lett,33(23):L23312.
Zollo A,Iannaccone G,Lancieri M,Cantore L,Convertito V,Emolo A,Festa G,lovič F,Vassallo M,Martino C,Satriano C,Gasparini P. 2009. Earthquake early warning system in southern Italy:Methodologies and performance evaluation[J]. Geophys Res Lett,36(5):L00B07.
-
期刊类型引用(10)
1. 刘奕均，杨光亮，王嘉沛，谈洪波，周怀斌，申重阳. 基于粒子群算法的四川长宁地区印支构造界面反演. 地震地质. 2023(01): 172-189 . 
百度学术
2. 罗嘉琦，帅向华，李继赓. 基于深度学习的倾斜摄影建筑物表面损毁信息提取. 中国地震. 2023(02): 271-281 . 百度学术
3. 龚丽文，张怀，陈石，David A.Yuen，陈丽娟，Brennan Brunsvik，尹光耀. 基于机器学习的长宁地震三维断层面几何特征建模. 地震学报. 2023(06): 1040-1054 . 本站查看
4. 扈桂让，张广伟，梁姗姗. 四川长宁地区地震活动空间分布特征研究. 中国地震. 2023(04): 883-892 . 百度学术
5. 李洪丽，刘财，田有，闫冬，李志强. 地震走时层析成像方法在研究强震孕震、发生机制中的应用. 地球与行星物理论评. 2022(02): 148-158 . 百度学术
6. 于书媛，方良好，宴金旭，倪红玉，陈靓，丁娟. 运用InSAR技术解算四川长宁M_S6.0地震三维形变场及时间序列形变分析. 地震工程学报. 2022(06): 1469-1477+1488 . 百度学术
7. 李昌珑，温增平. 2020年地震危险性分析热点回眸. 科技导报. 2021(01): 97-104 . 百度学术
8. 赵韬，王莹，马冀，邵若潼，徐一斐，胡景. 2021年青海玛多7.4级地震序列重定位和震源机制特征. 地震地质. 2021(04): 790-805 . 百度学术
9. 路珍，郭志，黄伟亮，张佩，李君，张媛媛. 2009年陕西高陵M_L4.8地震震源参数及构造特征分析. 大地测量与地球动力学. 2021(11): 1157-1162 . 百度学术
10. 王月，胡少乾，何骁慧，郭凯，解孟雨，邓世广，马亚伟. 2021年5月21日云南漾濞6.4级地震序列重定位及震源机制研究. 地球物理学报. 2021(12): 4510-4525 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 188
- HTML全文浏览量: 34
- PDF下载量: 66
- 被引次数: 13
