Numerical simulation of near-field pulse-like ground motion for the Shuantung fault in Taiwan region
-
摘要: 根据我国台湾地区西部的地质地貌特征和1999年集集MW7.6地震的震源参数，建立了三维速度结构模型和两类震源模型。基于地壳中断层的位错积累量和岩石破裂后应力应变的传播特性，采用三维有限差分法对双冬断层活动可能产生的近场脉冲型地震动进行了模拟研究。结果表明：走滑断层垂直于断层走向的水平分量和逆断层垂直分量的峰值速度较大；由方向性效应所产生的双向速度脉冲主要集中在垂直于断层滑动分量方向，而由滑冲效应所产生的单向速度脉冲则主要集中在平行于断层滑动分量的方向；受方向性效应和上盘效应的共同制约，近场脉冲型地震动呈不对称带状分布，速度脉冲多分布在距离走滑断层迹线15 km和逆断层迹线10 km的范围内；速度反应谱在断层面的覆盖范围内沿破裂方向逐渐增大，且速度脉冲可能会对大型建筑物产生严重的剪切破坏。受凹凸体特性的影响，地震波场显示南投、台中和苗栗处于强地震动危险区。Abstract: Based on the geological and geomorphological characteristics of western Taiwan and the source parameters of the 1999 MW7.6 Jiji （Chi-Chi） earthquake, we have established a 3D velocity structure model and two types of source models. Based on the accumulation of dislocation in the crust and the propagation characteristics of stress and strain after the rock fracture, 3D finite difference method was used to simulate the near-field pulse-like ground motion that would occur in the Shuantung fault activity. The results show that the peak velocity of the horizontal component perpendicular to the fault strike of the strike-slip fault is large, and so is the peak velocity of the vertical component of the reverse fault. The double-sided velocity pulses generated by the directivity effect are mainly concentrated in the direction perpendicular to the fault sliding component, while the single-sided velocity pulses generated by the fling-step effect are mainly concentrated in the direction parallel to the fault sliding component. Because of the mutual control of the directivity effect and the hanging wall effect, the near-field pulse-like ground motions exhibit an asymmetrical zonal distribution, and the velocity pulses mostly distributed within 15 km from the strike-slip fault trace and 10 km from the reverse fault trace. The velocity response spectrum gradually increases along the rupture direction within the coverage of the fault plane, and the velocity pulse may cause severe shear damage to large buildings. Influenced by the characteristics of the asperities, the seismic wave field shows that Nantou, Taichung, and Miaoli are in risk region of strong ground motion.
-
引言
据中国地震台网中心测定，2018年5月28日1时50分52.5秒在吉林省松原市宁江区发生MS5.7地震，震中位置为（45.27°N，124.71°E），震源深度为13 km。哈尔滨、长春白城等地震感明显，地震造成震中地区部分房屋损毁，烈度达Ⅶ度，无人员伤亡。
松原MS5.7地震发生于松辽盆地内部，处于NNE-NE向的扶余—肇东断裂和NW向第二松花江断裂交会部位（图1）。该地区曾于1119年发生过M6¾地震（吴戈等，1988；唐雅芝，1988，1990）；近年来，松原地区地震活动强度和频度在东北地区最高，于2006年和2013年扶余—肇东断裂南端分别发生前郭MS5.0地震和MS5.8震群（图1）。此次松原MS5.7地震发生前，从2017年7月23日开始该地区先后发生了4次MS≥4.0地震及系列小震。此外，松原还是东北地区重要的石油开采区和经济文化聚集地，因此开展本区内地震构造、地震活动性的相关研究具有十分重要的意义。
![]()
图 1 研究区地质构造、历史地震及台站分布Figure 1. Regional geological structure and distribution of earthquake epicenters and seismic stations关于2013年前郭MS5.8震群的研究较多，如吴微微等（2014）、刘双庆等（2015）、刘俊清等（2017a，b）、盛书中等（2017）、李君和王勤彩（2018），这些研究从震源机制、小震精定位和烈度分布等方面取得的结果较为一致，均认为发震断层为NW向的查干泡—道字井断裂。而关于2018年松原MS5.7地震的研究结果较少，震源机制解显示此次地震为走滑型地震，存在NW和NE向两个节面，与第二松花江断裂和扶余—肇东断裂走向基本一致（杨文等，2018；盘晓东等，2018；李君等，2019）。小震精定位结果显示余震分布无明显方向性，不能确定发震断层（盘晓东等，2018；李君等，2019），而杨文等（2018）的研究结果显示MS5.7地震序列沿NE向展布。李君等（2019）根据松原MS5.7地震震源机制解的两个节面和断层性质判断该地震的发震断层为第二松花江断裂。而松原MS5.7地震等烈度线长轴为NE向（盘晓东等，2018）。上述研究结果对发震构造的认识也不尽一致，因此，确定此次地震的发震断层对深入研究该地区发震构造和应力场特征十分必要。
鉴于此，本文利用黑龙江省地震台网，以及吉林、内蒙古部分台站记录到的宽频带三分量地震波形数据，通过ISOLA软件（Sokos，Zahradník，2008，2013）对2018年5月28日发生在松原的MS5.7地震事件进行地震三分量全波形矩张量反演，获取此次地震的震源机制解和矩心位置。根据Zahradník等（2008a）的震源-矩心（hypocenter-centroid，缩写为H-C）方法分析了松原MS5.7地震矩心、震源和节面的相对位置从而推断发震断层。
引言
据中国地震台网中心测定，2018年5月28日1时50分52.5秒在吉林省松原市宁江区发生MS5.7地震，震中位置为（45.27°N，124.71°E），震源深度为13 km。哈尔滨、长春白城等地震感明显，地震造成震中地区部分房屋损毁，烈度达Ⅶ度，无人员伤亡。
松原MS5.7地震发生于松辽盆地内部，处于NNE-NE向的扶余—肇东断裂和NW向第二松花江断裂交会部位（图1）。该地区曾于1119年发生过M6¾地震（吴戈等，1988；唐雅芝，1988，1990）；近年来，松原地区地震活动强度和频度在东北地区最高，于2006年和2013年扶余—肇东断裂南端分别发生前郭MS5.0地震和MS5.8震群（图1）。此次松原MS5.7地震发生前，从2017年7月23日开始该地区先后发生了4次MS≥4.0地震及系列小震。此外，松原还是东北地区重要的石油开采区和经济文化聚集地，因此开展本区内地震构造、地震活动性的相关研究具有十分重要的意义。
![]()
图 1 研究区地质构造、历史地震及台站分布Figure 1. Regional geological structure and distribution of earthquake epicenters and seismic stations关于2013年前郭MS5.8震群的研究较多，如吴微微等（2014）、刘双庆等（2015）、刘俊清等（2017a，b）、盛书中等（2017）、李君和王勤彩（2018），这些研究从震源机制、小震精定位和烈度分布等方面取得的结果较为一致，均认为发震断层为NW向的查干泡—道字井断裂。而关于2018年松原MS5.7地震的研究结果较少，震源机制解显示此次地震为走滑型地震，存在NW和NE向两个节面，与第二松花江断裂和扶余—肇东断裂走向基本一致（杨文等，2018；盘晓东等，2018；李君等，2019）。小震精定位结果显示余震分布无明显方向性，不能确定发震断层（盘晓东等，2018；李君等，2019），而杨文等（2018）的研究结果显示MS5.7地震序列沿NE向展布。李君等（2019）根据松原MS5.7地震震源机制解的两个节面和断层性质判断该地震的发震断层为第二松花江断裂。而松原MS5.7地震等烈度线长轴为NE向（盘晓东等，2018）。上述研究结果对发震构造的认识也不尽一致，因此，确定此次地震的发震断层对深入研究该地区发震构造和应力场特征十分必要。
鉴于此，本文利用黑龙江省地震台网，以及吉林、内蒙古部分台站记录到的宽频带三分量地震波形数据，通过ISOLA软件（Sokos，Zahradník，2008，2013）对2018年5月28日发生在松原的MS5.7地震事件进行地震三分量全波形矩张量反演，获取此次地震的震源机制解和矩心位置。根据Zahradník等（2008a）的震源-矩心（hypocenter-centroid，缩写为H-C）方法分析了松原MS5.7地震矩心、震源和节面的相对位置从而推断发震断层。
1. 地震矩张量反演方法
本文选择Sokos和Zahradník （2008，2013）的ISOLA近震全波形矩张量反演方法计算松原MS5.7地震的矩张量解。ISOLA是基于单点源或多点源模型利用迭代反褶积方法，通过网格搜索得到地震最佳矩张量解。Kikuchi和Kanamori （1991）基于六元矩张量的反问题公式提出了使用方差减少（variance reduction，缩写为VR）快速评估观测波形与合成波形之间的相关性：VR＝1－E/O，其中E＝∑（Oi－Si）2，O＝∑Oi2，O和S分别表示观测波形和合成波形。VR为表征观测波形与合成波形拟合度的重要参数，最大值为1，VR越接近1，表明观测波形与合成波形的拟合度越高。反演过程中使用Bouchon （2003）的离散波数法来计算格林函数。通过网格搜索计算质心位置和质心时间。矩张量可以分解为三部分：双力偶（double couple，缩写为DC）、补偿线性矢量偶极子（compensated linear vector dipole，缩写为CLVD）和各向同性或体积分量（isotropic or volumetric component，缩写为ISO）。它们的相对大小以百分比表示，并且ISO＋CLVD＋DC＝1。当不考虑或忽略体积变化即ISO＝0时，得到的解称为偏矩张量解。本文更多考虑双力偶成分的变化，且由偏矩张量计算得到的标量矩、走向、倾角和滑动角结果可信（Zahradník et al，2008b），所以本文进行的矩张量反演均为偏矩张量反演。
波形反演频率的下限和上限分别由噪声（自然噪声或仪器噪声）与给定的震中距和速度模型质量决定（Fojtíková，Zahradník，2014）。信噪比（signal-to-noise ratio，缩写为SNR）根据振幅谱来评估（图2）。首先，由用户选择波形图上的信号时间窗口，然后系统自动选择噪声时间窗口，使其与信号时间窗具有相同长度，并在信号窗开始时结束。因此，噪声窗口位于信号窗口之前。对两个窗口分别计算振幅谱，并对地震动的每个分量分别进行平滑和绘制。信噪比是作为频率函数（信噪比曲线）计算的，用户在反演过程中选择滤波频带时，可以参考信噪比曲线。
![]()
图 2 IDR，BNX和GAN台站记录的松原MS5.7地震波形（a）、傅里叶谱（b）和信噪比（c）Figure 2. Seismic swarm of Songyuan MS5.7 event （a），Fourier amplitude spectra of the signals and noises （b） and the signal-to-noise ratios of three-component and mean values （c） for the stations IDR，BNX and GAN矩张量的可分辨性由条件数（condition number，缩写为CN）量化，CN是格林函数矩阵的最大奇异值与最小奇异值之比（Zahradník，Custódio，2012），是一个相对度量，该值的大小反映反演结果优劣。该方法细节请参阅Krizova等（2013）。
另外，震源机制变异指数（focal-mechanism variability index，缩写为FMVAR）和时空变异指数（space-time variability index，缩写为STVAR）通常也用来评价地震矩张量解的优劣，具体方法解释详见Sokos和Zahradník （2013）。
1. 地震矩张量反演方法
本文选择Sokos和Zahradník （2008，2013）的ISOLA近震全波形矩张量反演方法计算松原MS5.7地震的矩张量解。ISOLA是基于单点源或多点源模型利用迭代反褶积方法，通过网格搜索得到地震最佳矩张量解。Kikuchi和Kanamori （1991）基于六元矩张量的反问题公式提出了使用方差减少（variance reduction，缩写为VR）快速评估观测波形与合成波形之间的相关性：VR＝1－E/O，其中E＝∑（Oi－Si）2，O＝∑Oi2，O和S分别表示观测波形和合成波形。VR为表征观测波形与合成波形拟合度的重要参数，最大值为1，VR越接近1，表明观测波形与合成波形的拟合度越高。反演过程中使用Bouchon （2003）的离散波数法来计算格林函数。通过网格搜索计算质心位置和质心时间。矩张量可以分解为三部分：双力偶（double couple，缩写为DC）、补偿线性矢量偶极子（compensated linear vector dipole，缩写为CLVD）和各向同性或体积分量（isotropic or volumetric component，缩写为ISO）。它们的相对大小以百分比表示，并且ISO＋CLVD＋DC＝1。当不考虑或忽略体积变化即ISO＝0时，得到的解称为偏矩张量解。本文更多考虑双力偶成分的变化，且由偏矩张量计算得到的标量矩、走向、倾角和滑动角结果可信（Zahradník et al，2008b），所以本文进行的矩张量反演均为偏矩张量反演。
波形反演频率的下限和上限分别由噪声（自然噪声或仪器噪声）与给定的震中距和速度模型质量决定（Fojtíková，Zahradník，2014）。信噪比（signal-to-noise ratio，缩写为SNR）根据振幅谱来评估（图2）。首先，由用户选择波形图上的信号时间窗口，然后系统自动选择噪声时间窗口，使其与信号时间窗具有相同长度，并在信号窗开始时结束。因此，噪声窗口位于信号窗口之前。对两个窗口分别计算振幅谱，并对地震动的每个分量分别进行平滑和绘制。信噪比是作为频率函数（信噪比曲线）计算的，用户在反演过程中选择滤波频带时，可以参考信噪比曲线。
![]()
图 2 IDR，BNX和GAN台站记录的松原MS5.7地震波形（a）、傅里叶谱（b）和信噪比（c）Figure 2. Seismic swarm of Songyuan MS5.7 event （a），Fourier amplitude spectra of the signals and noises （b） and the signal-to-noise ratios of three-component and mean values （c） for the stations IDR，BNX and GAN矩张量的可分辨性由条件数（condition number，缩写为CN）量化，CN是格林函数矩阵的最大奇异值与最小奇异值之比（Zahradník，Custódio，2012），是一个相对度量，该值的大小反映反演结果优劣。该方法细节请参阅Krizova等（2013）。
另外，震源机制变异指数（focal-mechanism variability index，缩写为FMVAR）和时空变异指数（space-time variability index，缩写为STVAR）通常也用来评价地震矩张量解的优劣，具体方法解释详见Sokos和Zahradník （2013）。
2. 数据选择及处理
用于地震矩张量反演的波形选自黑龙江省区域测震台网的7个宽频带台站，以及吉林和内蒙古测震台网共享的4个宽频带台站，分布如图1所示。如表1所示，台站所使用的宽频带地震计主要以BBVS-60，Guralp CMG-3ESPC和CTS-1H/VBB为主，采样率为100 Hz，震中距最大为358 km，最小为170 km。
表 1 反演使用的宽频带台站仪器Table 1. Broadband station instruments for inversion序号 台站名 采样率/Hz 地震计 数采 震中距/km 1 IDR 100 BBVS-60 EDAS-24IP 216 2 QAN 100 BBVS-60 EDAS-24IP 269 3 NEH 100 Guralp CMG-3ESPC EDAS-24IP 358 4 NZN 100 CIS-1H/VBB EDAS-24IP 290 5 WLT 100 CIS-1H/VBB EDAS-24L 226 6 GAN 100 CIS-1H/VBB EDAS-24IP 313 7 WAK 100 BBVS-60 EDAS-24IP 222 8 BNX 100 CIS-1H/VBB EDAS-24IP 217 9 WUC 100 Guralp CMG-3ESPC EDAS-24IP 187 10 YST 100 BBVS-60 EDAS-24GN 170 11 FMT 100 BBVS-60 EDAS-24IP 231 本研究对每个台站三分量波形数据进行频谱分析和信噪比分析。图2为部分台站（BNX，GAN和IDR）记录到的MS5.7地震事件波形和频谱图，可以看出，当频率大于0.04 Hz时（图2b和c），所有台站波形均有一个较高的信噪比，因此，选择0.04 Hz为滤波频率下限。但是，个别台站的个别分量（如2a中GAN台站的UD分量）信噪比较差，在反演过程中得到的合成波形与观测波形拟合较差，因此，在优化反演过程中信噪比明显偏低的分量将不参与反演。滤波频率上限是根据地震的震中距和地震波剪切波波长确定，对于震中距小于300 km的台站反演波形频率上限一般为0.1 Hz （Zahradník et al，2005；Benetatos et al，2013），由于本文研究台站，其最大震中距为358 km，所以选择滤波频率上限为0.09 Hz。因此，本文选取的滤波频率范围为0.04—0.09 Hz，为了求取最优解，反演过程中还会在此范围内选择最优滤波频率。
地壳速度结构能够提供有关震源及震源介质的重要信息，是影响矩张量解的重要因素。本文对比了CRUST1.0、吴微微等（2014）和刘俊清等（2017a）给出的吉林松原地区一维速度模型（图3），通过试错，使用ISOLA软件在其它参数不变情况下，计算了四种速度模型下松原MS5.7地震的震源机制解，结果列于表2，可以看出，由不同速度模型得到的结果相差很小，本文选用具有较高VR值和DC值的吴微微等（2014）的一维速度模型作为反演的速度模型。
表 2 不同速度模型计算出的地震矩张量结果对比Table 2. Comparison of moment tensor solutions calculated by different velocity models速度模型 节面 走向/° 倾角/° 滑动角/° VR DC MW 矩心深度/km CRUST1.0 Ⅰ 217 77 162 64% 60.8% 5.1 6 Ⅱ 311 73 14 吴微微等（2014） Ⅰ 216 75 159 74% 73.3% 5.1 6 Ⅱ 312 70 16 刘俊清等（2017a）VM-1 Ⅰ 216 77 160 70% 70.4% 5.1 6 Ⅱ 311 71 13 刘俊清等（2017a）VM-3 Ⅰ 219 85 171 56% 53.9% 5.2 6 Ⅱ 310 81 5 2. 数据选择及处理
用于地震矩张量反演的波形选自黑龙江省区域测震台网的7个宽频带台站，以及吉林和内蒙古测震台网共享的4个宽频带台站，分布如图1所示。如表1所示，台站所使用的宽频带地震计主要以BBVS-60，Guralp CMG-3ESPC和CTS-1H/VBB为主，采样率为100 Hz，震中距最大为358 km，最小为170 km。
表 1 反演使用的宽频带台站仪器Table 1. Broadband station instruments for inversion序号 台站名 采样率/Hz 地震计 数采 震中距/km 1 IDR 100 BBVS-60 EDAS-24IP 216 2 QAN 100 BBVS-60 EDAS-24IP 269 3 NEH 100 Guralp CMG-3ESPC EDAS-24IP 358 4 NZN 100 CIS-1H/VBB EDAS-24IP 290 5 WLT 100 CIS-1H/VBB EDAS-24L 226 6 GAN 100 CIS-1H/VBB EDAS-24IP 313 7 WAK 100 BBVS-60 EDAS-24IP 222 8 BNX 100 CIS-1H/VBB EDAS-24IP 217 9 WUC 100 Guralp CMG-3ESPC EDAS-24IP 187 10 YST 100 BBVS-60 EDAS-24GN 170 11 FMT 100 BBVS-60 EDAS-24IP 231 本研究对每个台站三分量波形数据进行频谱分析和信噪比分析。图2为部分台站（BNX，GAN和IDR）记录到的MS5.7地震事件波形和频谱图，可以看出，当频率大于0.04 Hz时（图2b和c），所有台站波形均有一个较高的信噪比，因此，选择0.04 Hz为滤波频率下限。但是，个别台站的个别分量（如2a中GAN台站的UD分量）信噪比较差，在反演过程中得到的合成波形与观测波形拟合较差，因此，在优化反演过程中信噪比明显偏低的分量将不参与反演。滤波频率上限是根据地震的震中距和地震波剪切波波长确定，对于震中距小于300 km的台站反演波形频率上限一般为0.1 Hz （Zahradník et al，2005；Benetatos et al，2013），由于本文研究台站，其最大震中距为358 km，所以选择滤波频率上限为0.09 Hz。因此，本文选取的滤波频率范围为0.04—0.09 Hz，为了求取最优解，反演过程中还会在此范围内选择最优滤波频率。
地壳速度结构能够提供有关震源及震源介质的重要信息，是影响矩张量解的重要因素。本文对比了CRUST1.0、吴微微等（2014）和刘俊清等（2017a）给出的吉林松原地区一维速度模型（图3），通过试错，使用ISOLA软件在其它参数不变情况下，计算了四种速度模型下松原MS5.7地震的震源机制解，结果列于表2，可以看出，由不同速度模型得到的结果相差很小，本文选用具有较高VR值和DC值的吴微微等（2014）的一维速度模型作为反演的速度模型。
表 2 不同速度模型计算出的地震矩张量结果对比Table 2. Comparison of moment tensor solutions calculated by different velocity models速度模型 节面 走向/° 倾角/° 滑动角/° VR DC MW 矩心深度/km CRUST1.0 Ⅰ 217 77 162 64% 60.8% 5.1 6 Ⅱ 311 73 14 吴微微等（2014） Ⅰ 216 75 159 74% 73.3% 5.1 6 Ⅱ 312 70 16 刘俊清等（2017a）VM-1 Ⅰ 216 77 160 70% 70.4% 5.1 6 Ⅱ 311 71 13 刘俊清等（2017a）VM-3 Ⅰ 219 85 171 56% 53.9% 5.2 6 Ⅱ 310 81 5 3. 矩张量反演结果
首先使用全部11个台站波形，以MS5.7地震震中位置为中心，在其下方2—15 km 深度（步长1 km），在0.04—0.09 Hz滤波频带内反演矩心位置，得到初步结果，如图4和表3中第一行测试1所示，可见在3—8 km深度矩张量解参数变化不大，具有较好的稳定性，最优解深度为6 km，该深度解显示VR值为74%和较高的双力偶成分占73.3%。该解在深度和时间上具有较大的稳定性，矩张量在最佳走向、倾角和滑动角附近略有变化。由于所选台站中有些震中距较大，有些台站的方位角重叠，而且使用ISOLA进行波形反演对台站方位角的覆盖和台站数量要求不高。于是，在此基础上进一步优化台站选择和滤波频率范围，通过试错，最终反演结果列于表3，可以看出选择NZN，IDR，WLT，WAK，BNX，YST和FMT等7个台站在0.05—0.08 Hz频带内进行反演得到的解进一步优化，震源机制解较为稳定，VR值（88%）和DC值（93.5%）有明显提升。因此，在固定震中位置为矩心位置进行深度反演时的矩张量最优解为：矩心深度为6 km；节面Ⅰ的走向、倾角和滑动角分别为214°，69°和154°；节面Ⅱ的走向、倾角和滑动角分别为313°，66°和23°；DC＝93.5%，VR＝88%，MW＝5.2。本文反演的两次结果与USGS，GFZ和李君等（2019）结果基本一致（表3），表明反演结果可信。下文进行的反演均在表3测试2的台站选择和滤波频率下进行。
表 3 不同震源机制计算结果对比Table 3. Comparison of focal mechanisms from different agency or researchers来源 MW 矩心深度/km 节面Ⅰ 节面Ⅱ DC VR 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 测试1 5.1 6 216 75 159 312 70 16 73.3% 74% 测试2 5.2 6 214 69 154 313 66 23 93.5% 88% 李君等（2019） − 6 220 79 162 314 72 12 − − GFZ （2018） 5.2 14 223 77 180 313 90 13 − − USGS （2018） 5.3 12 47 68 −169 313 80 −22 64% − 注：测试1为利用本文选择的全部11个宽频带台站反演的结果，测试2为利用NZN，IDR，WLT，WAK，BNX，YST和FMT等7个
宽频带台站反演结果![]()
图 4 松原MS5.7地震矩心深度与波形互相关系数Figure 4. Centroid depth versus cross-correlation coefficient for the MS5.7 Songyuan event矩心代表地震破裂区的重心。矩心可以在矩张量反演过程中确定，通过在假定位置周围进行网格搜索找到一个最优的波形拟合的点。对于一次MS4.0的地震事件，震源-矩心距离与其定位误差相当，甚至更小。因此，对于小的地震事件矩心可视为震源位置。对于MS5.7地震，其破裂尺度一般在七至十几千米不等，震源与矩心不重合。
在前述确定最佳矩心深度为6 km的基础上，以震中位置为中心，在0.05—0.08 Hz滤波频带内使用偏矩张量反演在水平面上进行网格搜索矩心位置，分别在5 km，6 km，7 km和8 km深度建立11×9个1 km×1 km的网格进行反演矩心位置。观测波形与合成波形相关性空间分布如图5所示，可以明确看出：相对于原始震中定位，矩心发生了偏移；矩心的最佳位置位于震中南侧5 km，西侧2 km处；在深度6 km和7 km处方差减少量最大，即VR＝93%，而这两个深度处得到的解（走向、倾角和滑动角）非常相似。本文选取7 km深度的矩张量解，因为它具有更小的FMVAR值（FMVAR＝12±7）和更高的双力偶成分（96.4%）。该深度矩心位置为（45.225°N，124.685°E）；节面Ⅰ的走向、倾角和滑动角分别为217°，82°和164°，节面Ⅱ的走向、倾角和滑动角分别为309°，74°和8°，DC＝96.4%，VR＝93%，MW5.2 （图6）。合成波形与观测波形的拟合如图7所示，其中台站IDR的NS向波形未参与反演。
![]()
图 5 不同深度网格平面观测波形与合成波形之间相关性Figure 5. Plot of correlation between observed and synthetic records for horizontal grids with different depth![]()
图 6 ISOLA软件反演松原MS5.7地震矩张量最终结果Figure 6. The final centroid position of Songyuan MS5.7 event from seismic moment inversion by ISOLA![]()
3. 矩张量反演结果
首先使用全部11个台站波形，以MS5.7地震震中位置为中心，在其下方2—15 km 深度（步长1 km），在0.04—0.09 Hz滤波频带内反演矩心位置，得到初步结果，如图4和表3中第一行测试1所示，可见在3—8 km深度矩张量解参数变化不大，具有较好的稳定性，最优解深度为6 km，该深度解显示VR值为74%和较高的双力偶成分占73.3%。该解在深度和时间上具有较大的稳定性，矩张量在最佳走向、倾角和滑动角附近略有变化。由于所选台站中有些震中距较大，有些台站的方位角重叠，而且使用ISOLA进行波形反演对台站方位角的覆盖和台站数量要求不高。于是，在此基础上进一步优化台站选择和滤波频率范围，通过试错，最终反演结果列于表3，可以看出选择NZN，IDR，WLT，WAK，BNX，YST和FMT等7个台站在0.05—0.08 Hz频带内进行反演得到的解进一步优化，震源机制解较为稳定，VR值（88%）和DC值（93.5%）有明显提升。因此，在固定震中位置为矩心位置进行深度反演时的矩张量最优解为：矩心深度为6 km；节面Ⅰ的走向、倾角和滑动角分别为214°，69°和154°；节面Ⅱ的走向、倾角和滑动角分别为313°，66°和23°；DC＝93.5%，VR＝88%，MW＝5.2。本文反演的两次结果与USGS，GFZ和李君等（2019）结果基本一致（表3），表明反演结果可信。下文进行的反演均在表3测试2的台站选择和滤波频率下进行。
表 3 不同震源机制计算结果对比Table 3. Comparison of focal mechanisms from different agency or researchers来源 MW 矩心深度/km 节面Ⅰ 节面Ⅱ DC VR 走向/° 倾角/° 滑动角/° 走向/° 倾角/° 滑动角/° 测试1 5.1 6 216 75 159 312 70 16 73.3% 74% 测试2 5.2 6 214 69 154 313 66 23 93.5% 88% 李君等（2019） − 6 220 79 162 314 72 12 − − GFZ （2018） 5.2 14 223 77 180 313 90 13 − − USGS （2018） 5.3 12 47 68 −169 313 80 −22 64% − 注：测试1为利用本文选择的全部11个宽频带台站反演的结果，测试2为利用NZN，IDR，WLT，WAK，BNX，YST和FMT等7个
宽频带台站反演结果![]()
图 4 松原MS5.7地震矩心深度与波形互相关系数Figure 4. Centroid depth versus cross-correlation coefficient for the MS5.7 Songyuan event矩心代表地震破裂区的重心。矩心可以在矩张量反演过程中确定，通过在假定位置周围进行网格搜索找到一个最优的波形拟合的点。对于一次MS4.0的地震事件，震源-矩心距离与其定位误差相当，甚至更小。因此，对于小的地震事件矩心可视为震源位置。对于MS5.7地震，其破裂尺度一般在七至十几千米不等，震源与矩心不重合。
在前述确定最佳矩心深度为6 km的基础上，以震中位置为中心，在0.05—0.08 Hz滤波频带内使用偏矩张量反演在水平面上进行网格搜索矩心位置，分别在5 km，6 km，7 km和8 km深度建立11×9个1 km×1 km的网格进行反演矩心位置。观测波形与合成波形相关性空间分布如图5所示，可以明确看出：相对于原始震中定位，矩心发生了偏移；矩心的最佳位置位于震中南侧5 km，西侧2 km处；在深度6 km和7 km处方差减少量最大，即VR＝93%，而这两个深度处得到的解（走向、倾角和滑动角）非常相似。本文选取7 km深度的矩张量解，因为它具有更小的FMVAR值（FMVAR＝12±7）和更高的双力偶成分（96.4%）。该深度矩心位置为（45.225°N，124.685°E）；节面Ⅰ的走向、倾角和滑动角分别为217°，82°和164°，节面Ⅱ的走向、倾角和滑动角分别为309°，74°和8°，DC＝96.4%，VR＝93%，MW5.2 （图6）。合成波形与观测波形的拟合如图7所示，其中台站IDR的NS向波形未参与反演。
![]()
图 5 不同深度网格平面观测波形与合成波形之间相关性Figure 5. Plot of correlation between observed and synthetic records for horizontal grids with different depth![]()
图 6 ISOLA软件反演松原MS5.7地震矩张量最终结果Figure 6. The final centroid position of Songyuan MS5.7 event from seismic moment inversion by ISOLA![]()
4. 地震发震断层判断
Zahradník等（2008a）提出了一种简单、有效判断发震断层的方法，称为震源-矩心方法（hypocenter-centroid method，缩写为H-C），其中：震源位置是地震破裂开始的地方；矩心位置是断层上主要滑动区域的点源近似。该方法尤其适用于走滑发震断层的判断。H-C方法的原理是将震源和矩心（在节面Ⅰ与节面Ⅱ交线上）投影到三维空间，然后计算震源到两个节面的距离。如果震源位于一个节面上，那么这个节面就是真实的发震断层。如果震源不在任何一个节面上，那么距离震源最近的那个节面就是真实发震断层。
由于所使用的定位台站和方法不同，震源定位结果也不尽相同，不同机构定位结果见表4。我们使用黑龙江省地震台网的地震台站和内蒙古、吉林台网部分共享台站的资料，利用HYPOINVERSE 2000 （Klein，1989）对松原MS5.7地震进行了重定位，震中位置为（45.27°N，124.77°E），深度为8.1 km，水平误差为1.1 km，垂直误差为2.0 km，残差为0.18。①
表 4 松原MS5.7地震基本参数Table 4. Basic parameters of Songyuan MS5.7 event编号 发震时间 震中位置 MS 震源深度/km 震中位置 结果来源 年-月-日 时： 分： 秒 北纬/° 东经/° 1 2018-05-28 01： 50： 52.5 45.31 124.69 5.7 10 松原市宁江区 中国地震台网（2018） 2 2018-05-28 01： 50： 52.6 45.27 124.71 5.7 10 松原市宁江区 刘俊清等① 3 2018-05-28 01： 50： 52.6 45.24 124.64 5.3 10 扶余 USGS（2018） 4 2018-05-28 01： 50： 53.9 45.33 124.42 5.2 （MW） 10 东北 GFZ（2018） 5 2018-05-28 01： 50： 52.5 45.27 124.77 5.7 8.1 松原市宁江区 本文 下面分别使用中国地震台网中心（2018）、刘俊清等①和本文所获定位结果的震源定位信息，与本文反演得到的矩心位置和两个节面进行分析。图8给出了松原MS5.7地震事件震源-矩心方法分析结果，显示本文定位结果与矩心的距离是8.43 km，距离节面Ⅰ（绿色）2.46 km，距离节面Ⅱ（红色）7.52 km。刘俊清等①的定位结果与矩心、节面Ⅰ和距离节面Ⅱ的距离分别为6.17 km，0.98 km和4.12 km，中国地震台网中心（2018）定位结果与矩心、节面Ⅰ和距离节面Ⅱ的距离分别为9.92 km，4.87 km和6.49 km。三个定位结果虽然稍有偏差，但是都显示节面Ⅰ是发震断层面，该节面与扶余—肇东断裂走向一致，所以据此判断扶余—肇东断裂为此次地震的发震断层。
4. 地震发震断层判断
Zahradník等（2008a）提出了一种简单、有效判断发震断层的方法，称为震源-矩心方法（hypocenter-centroid method，缩写为H-C），其中：震源位置是地震破裂开始的地方；矩心位置是断层上主要滑动区域的点源近似。该方法尤其适用于走滑发震断层的判断。H-C方法的原理是将震源和矩心（在节面Ⅰ与节面Ⅱ交线上）投影到三维空间，然后计算震源到两个节面的距离。如果震源位于一个节面上，那么这个节面就是真实的发震断层。如果震源不在任何一个节面上，那么距离震源最近的那个节面就是真实发震断层。
由于所使用的定位台站和方法不同，震源定位结果也不尽相同，不同机构定位结果见表4。我们使用黑龙江省地震台网的地震台站和内蒙古、吉林台网部分共享台站的资料，利用HYPOINVERSE 2000 （Klein，1989）对松原MS5.7地震进行了重定位，震中位置为（45.27°N，124.77°E），深度为8.1 km，水平误差为1.1 km，垂直误差为2.0 km，残差为0.18。①
表 4 松原MS5.7地震基本参数Table 4. Basic parameters of Songyuan MS5.7 event编号 发震时间 震中位置 MS 震源深度/km 震中位置 结果来源 年-月-日 时： 分： 秒 北纬/° 东经/° 1 2018-05-28 01： 50： 52.5 45.31 124.69 5.7 10 松原市宁江区 中国地震台网（2018） 2 2018-05-28 01： 50： 52.6 45.27 124.71 5.7 10 松原市宁江区 刘俊清等① 3 2018-05-28 01： 50： 52.6 45.24 124.64 5.3 10 扶余 USGS（2018） 4 2018-05-28 01： 50： 53.9 45.33 124.42 5.2 （MW） 10 东北 GFZ（2018） 5 2018-05-28 01： 50： 52.5 45.27 124.77 5.7 8.1 松原市宁江区 本文 下面分别使用中国地震台网中心（2018）、刘俊清等①和本文所获定位结果的震源定位信息，与本文反演得到的矩心位置和两个节面进行分析。图8给出了松原MS5.7地震事件震源-矩心方法分析结果，显示本文定位结果与矩心的距离是8.43 km，距离节面Ⅰ（绿色）2.46 km，距离节面Ⅱ（红色）7.52 km。刘俊清等①的定位结果与矩心、节面Ⅰ和距离节面Ⅱ的距离分别为6.17 km，0.98 km和4.12 km，中国地震台网中心（2018）定位结果与矩心、节面Ⅰ和距离节面Ⅱ的距离分别为9.92 km，4.87 km和6.49 km。三个定位结果虽然稍有偏差，但是都显示节面Ⅰ是发震断层面，该节面与扶余—肇东断裂走向一致，所以据此判断扶余—肇东断裂为此次地震的发震断层。
5. 讨论
通过H-C方法验证了扶余—肇东断裂为松原MS5.7地震的发震断层，该结果与反演得到的震源机制解的节面I走向、倾角较为一致，且与地震等烈度线长轴方向（盘晓东等，2018）一致。余震的分布情况有助于我们判断发震断层面，但是李君等（2019）和刘俊清等①的余震精定位分析结果显示余震没有明显的方向性展布，无法帮助判断发震断层。震源机制解显示此次地震为走滑型地震，两个节面分别与扶余—肇东断裂和第二松花江断裂走向一致，并且相关文献（李传友等，1999；刘权峰等，2017；吕晗，2017；刘俊清，2018）显示，对扶余—肇东断裂的描述为逆冲型，看上去似乎与震源机制显示的走滑型相矛盾，李君等（2019）也据此认为第二松花江断裂为发震断层。但是，本文也注意到刘权峰等（2017a，b）和刘俊清（2018）对扶余—肇东断裂最新活动时代描述为晚更新世，而这并不能代表现今的地壳运动状态，中国地震局第一监测中心（2018）的GPS应变图就能够很好地证明（1999—2007年、2009—2013年和2013—2015年三个阶段GPS应变图表明东北地区主应变具有明显变化）。于吉鹏等（2019）的研究表明2012—2017年松原地区主压应力方向为北东向，方向与北东向扶余—肇东断裂的走向一致，因此，有助于断裂发生走滑破裂。常金龙②利用2018年1—7月GPS基站数据，分别以内蒙古乌兰浩特（NMWL）、吉林长岭（JLCL）和长春（CHAN）三个台站为基准，分析大庆肇源（DQZY）基站的相对位置变化，其结果显示DQZY相对于三个参考点均有北东向运动的特点，长轴方向与扶余—肇东断裂走向基本一致（图9）。考虑到DQZY距离吉林松原MS5.7地震震中仅几十千米的距离，所以该点的运动状态基本可以反映地震前后震中位置的断裂活动变化。所以GPS资料表明松原MS5.7地震前后区域应力状态和GPS基站相对变化分析也都支持扶余—肇东断裂为发震断裂的判定。
![]()
图 9 松原MS5.7地震前后GPS基站位置相对变化上行三小图分别为DQZY站相对于NMWL，JLCL和CHAN三个基站位置变化示意图Figure 9. Relative variation of GPS station around Songyuan MS5.7 eventThe three pictures at the top of the figure are the relative changes of DQZY station relative to NMWL，JLCL and CHAN stations，respectively综上所述，就目前所掌握的信息，本文认为扶余—肇东断裂为2018年5月27日MS5.7地震的发震断裂。
5. 讨论
通过H-C方法验证了扶余—肇东断裂为松原MS5.7地震的发震断层，该结果与反演得到的震源机制解的节面I走向、倾角较为一致，且与地震等烈度线长轴方向（盘晓东等，2018）一致。余震的分布情况有助于我们判断发震断层面，但是李君等（2019）和刘俊清等①的余震精定位分析结果显示余震没有明显的方向性展布，无法帮助判断发震断层。震源机制解显示此次地震为走滑型地震，两个节面分别与扶余—肇东断裂和第二松花江断裂走向一致，并且相关文献（李传友等，1999；刘权峰等，2017；吕晗，2017；刘俊清，2018）显示，对扶余—肇东断裂的描述为逆冲型，看上去似乎与震源机制显示的走滑型相矛盾，李君等（2019）也据此认为第二松花江断裂为发震断层。但是，本文也注意到刘权峰等（2017a，b）和刘俊清（2018）对扶余—肇东断裂最新活动时代描述为晚更新世，而这并不能代表现今的地壳运动状态，中国地震局第一监测中心（2018）的GPS应变图就能够很好地证明（1999—2007年、2009—2013年和2013—2015年三个阶段GPS应变图表明东北地区主应变具有明显变化）。于吉鹏等（2019）的研究表明2012—2017年松原地区主压应力方向为北东向，方向与北东向扶余—肇东断裂的走向一致，因此，有助于断裂发生走滑破裂。常金龙②利用2018年1—7月GPS基站数据，分别以内蒙古乌兰浩特（NMWL）、吉林长岭（JLCL）和长春（CHAN）三个台站为基准，分析大庆肇源（DQZY）基站的相对位置变化，其结果显示DQZY相对于三个参考点均有北东向运动的特点，长轴方向与扶余—肇东断裂走向基本一致（图9）。考虑到DQZY距离吉林松原MS5.7地震震中仅几十千米的距离，所以该点的运动状态基本可以反映地震前后震中位置的断裂活动变化。所以GPS资料表明松原MS5.7地震前后区域应力状态和GPS基站相对变化分析也都支持扶余—肇东断裂为发震断裂的判定。
![]()
图 9 松原MS5.7地震前后GPS基站位置相对变化上行三小图分别为DQZY站相对于NMWL，JLCL和CHAN三个基站位置变化示意图Figure 9. Relative variation of GPS station around Songyuan MS5.7 eventThe three pictures at the top of the figure are the relative changes of DQZY station relative to NMWL，JLCL and CHAN stations，respectively综上所述，就目前所掌握的信息，本文认为扶余—肇东断裂为2018年5月27日MS5.7地震的发震断裂。
6. 结论
本文采用ISOLA软件对2018年5月28日吉林松原MS5.7地震进行了地震矩张量反演，结果显示在5—8 km深度的震源机制解较为稳定，与其他机构结果较为一致，结果可信。进一步使用网格搜索法在5—8 km深度反演搜索最佳矩心位置，最终确定最佳解为：矩心位置为（45.225°N，124.685°E）；矩心深度为7 km；节面Ⅰ的走向、倾角和滑动角分别为217°，82°和164°；节面Ⅱ的走向、倾角和滑动角分别为309°，74°和8°；DC＝96.4%，VR＝93%，矩震级为MW5.2。
进一步使用H-C方法分析了震源、矩心与节面之间的关系，推断扶余—肇东断裂为此次地震的发震断层。计算得到的震源机制似乎与地震地质资料相矛盾，但是GPS资料分析显示了现今吉林松原地区的应力状态，结果与之前的判断相一致。
总之，本文的计算与分析表明2018年5月28日松原MS5.7地震的发震断层为NE向扶余—肇东断裂，为走滑型地震。
两位审稿专家对本文修改提出的宝贵的意见，作者在此表示衷心感谢！
6. 结论
本文采用ISOLA软件对2018年5月28日吉林松原MS5.7地震进行了地震矩张量反演，结果显示在5—8 km深度的震源机制解较为稳定，与其他机构结果较为一致，结果可信。进一步使用网格搜索法在5—8 km深度反演搜索最佳矩心位置，最终确定最佳解为：矩心位置为（45.225°N，124.685°E）；矩心深度为7 km；节面Ⅰ的走向、倾角和滑动角分别为217°，82°和164°；节面Ⅱ的走向、倾角和滑动角分别为309°，74°和8°；DC＝96.4%，VR＝93%，矩震级为MW5.2。
进一步使用H-C方法分析了震源、矩心与节面之间的关系，推断扶余—肇东断裂为此次地震的发震断层。计算得到的震源机制似乎与地震地质资料相矛盾，但是GPS资料分析显示了现今吉林松原地区的应力状态，结果与之前的判断相一致。
总之，本文的计算与分析表明2018年5月28日松原MS5.7地震的发震断层为NE向扶余—肇东断裂，为走滑型地震。
两位审稿专家对本文修改提出的宝贵的意见，作者在此表示衷心感谢！
-
![]()
图 1 研究区内断层分布和本文假设断层面在地表的投影
Figure 1. The distribution of faults （solid lines） in the studied area and the projection of the fault plane at the surface （dashed box） assumed in this paper
![]()
图 2 断层模型示意图
红色区域Ⅰ和Ⅱ分别表示两个凹凸体，蓝色弧线表示破裂方式及传播时间
Figure 2. Sketch of the fault model
The red areas Ⅰ and Ⅱ indicate two asperities，the blue arc indicates the rupture model and propagation time
![]()
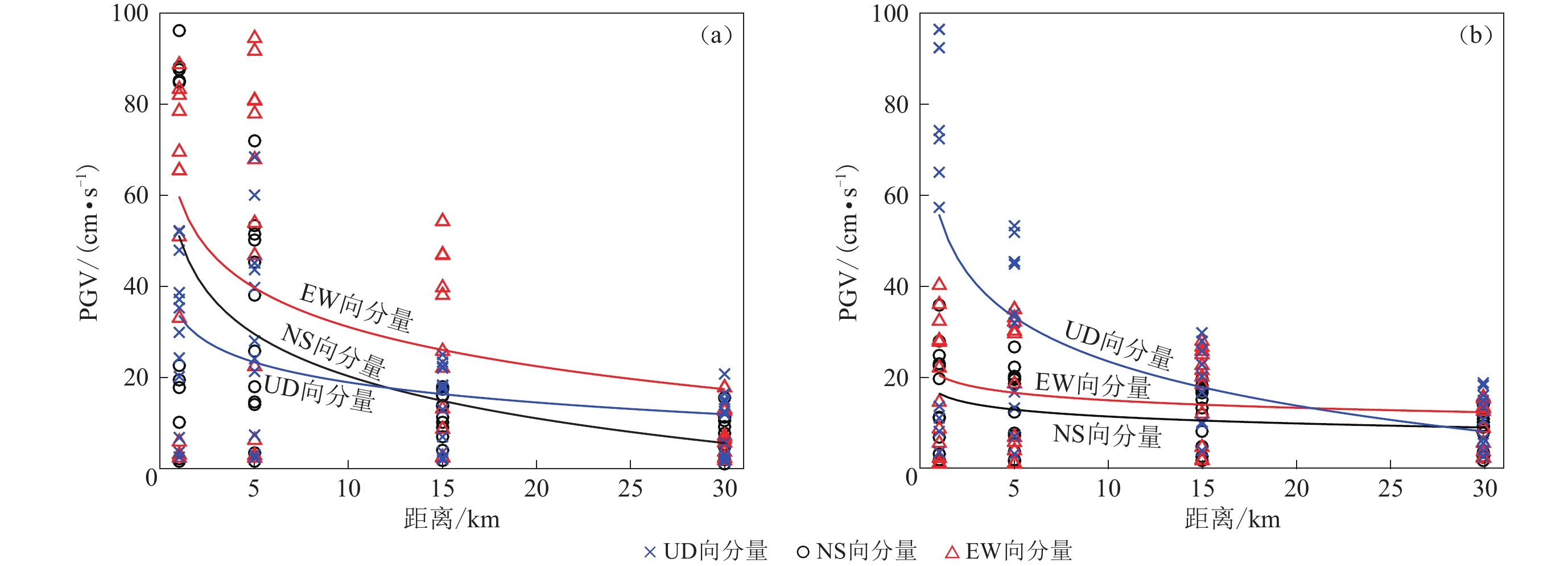
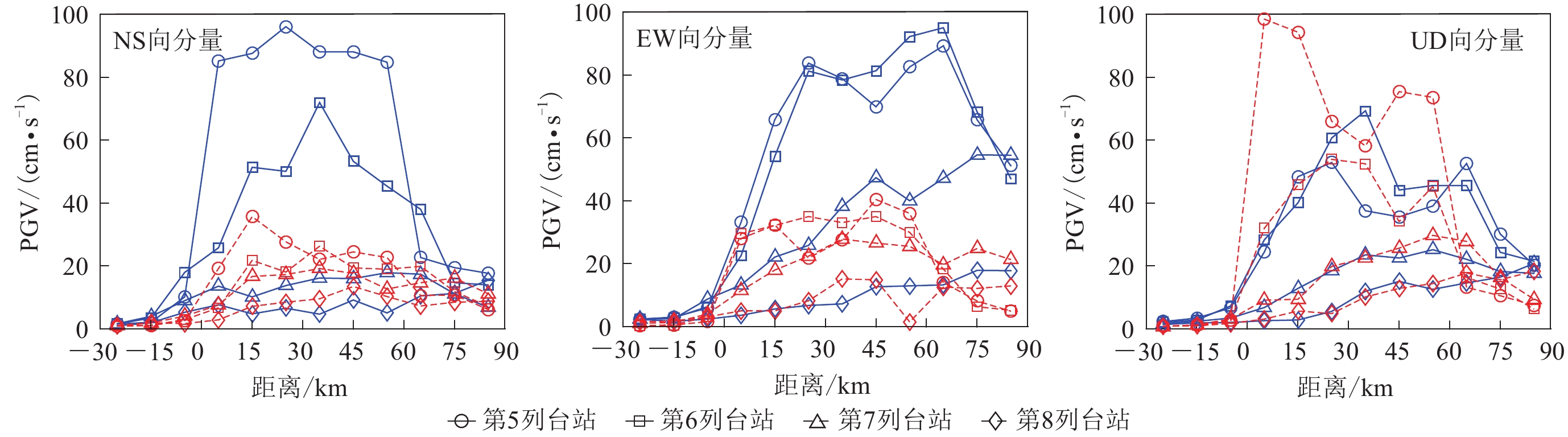
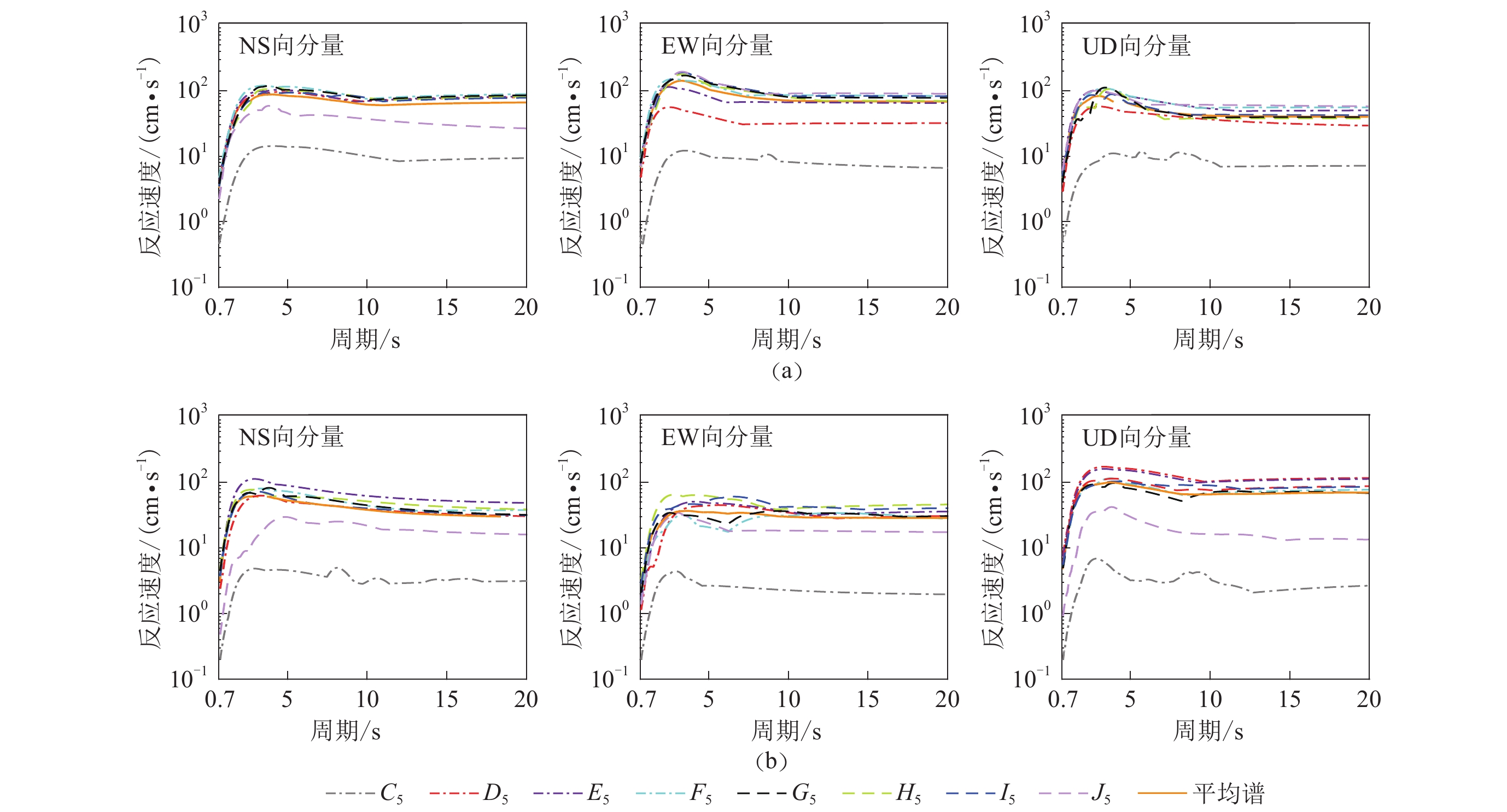
图 3 走滑断层（a）和逆断层（b）在多个台站的三分量速度时程
每个子图中从上到下为C5，D5，···，J5等台站相应的速度时程，PGV的单位为cm/s
Figure 3. Three-component velocity time histories at the stations for strike-slip fault （a） and reverse fault （b）
Each subgraph from top to bottom corresponds to the velocity time history of stations such as C5，D5，···，J5，the unit of PGV is cm/s
![]()
图 4 走滑断层（a）和逆断层（b）上盘内的台站三分量峰值速度（PGV）沿垂直于断层走向的变化
Figure 4. Variation of three-component peak ground velocity （PGV） along the direction perpendicular to the fault strike at the stations of the hanging wall for strike-slip fault （a） and reverse fault （b）
![]()
图 5 走滑断层（蓝色实线）和逆断层（红色虚线）上盘内的台站三分量峰值速度（PGV）沿断层走向的变化
Figure 5. Variation of three-component peak ground velocity （PGV） along the fault strike on the hanging wall for strike-slip fault （blue solid line） and reverse fault （red dashed line）
![]()
图 6 真实地震和模拟地震的脉冲记录随断层距的分布
Figure 6. Distribution of pulse recordings with fault distance for the real earthquakes and simulated earthquakes
![]()
图 7 走滑断层（a）和逆断层（b）的峰值速度（PGV）等值线图
Figure 7. Peak ground velocity contour maps of strike-slip fault （a） and reverse fault （b）
![]()
图 8 走滑断层（a）和逆断层（b）在C5−J5台站的三分量速度反应谱
Figure 8. Three-component velocity response spectrum at the stations of C5−J5 for strike-slip fault （a） and reverse fault （b）
![]()
图 9 走滑断层在地震过程中不同时刻的地面运动波场快照
Figure 9. Snapshots of the wave field at different moments for the ground motion of strike-slip fault
表 1 研究区域地壳参数
Table 1 Structure parameters for the studied area
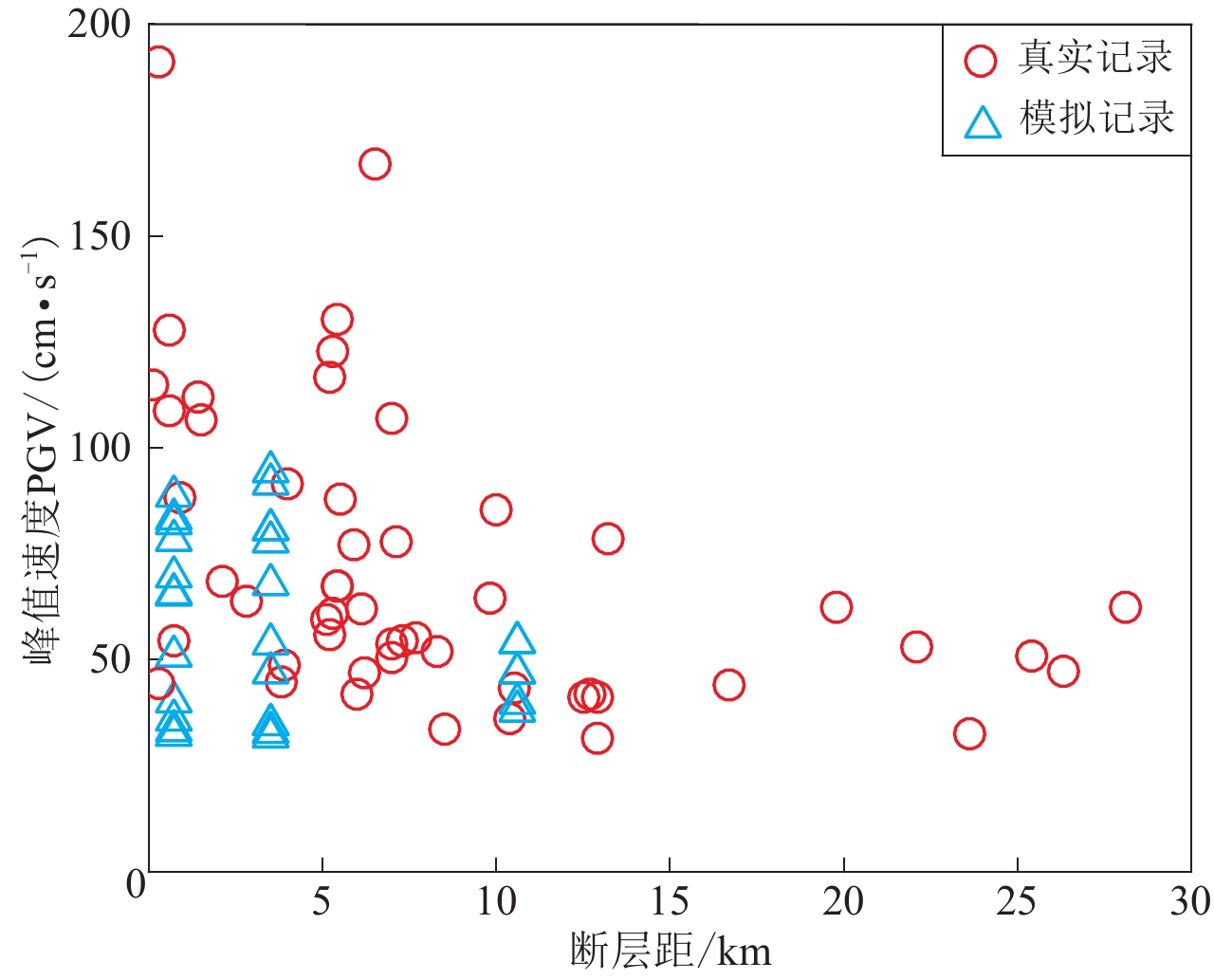
层序号 深度/km vP/（km·s−1） vS/（km·s−1） 密度/（103 kg·m−3） Q 1 2 4.66 2.57 2.25 250 2 5 5.45 2.67 2.45 250 3 10 5.76 2.88 2.55 300 4 15 6.15 3.31 2.60 300 5 25 6.71 3.72 2.90 500 6 30 7.11 4.07 3.15 500 
下载: 导出CSV
表 2 真实脉冲型地震记录的参数
Table 2 Parameters of pulse-like earthquakes
地震名称 发震日期 MW 记录数 帝王谷地震 1979−10−15 6.5 15 北岭地震 1994−01−17 6.7 11 集集地震 1999−09−21 7.6 26
下载: 导出CSV
-
高孟潭,俞言祥,张晓梅,吴健,胡平,丁彦慧. 2002. 北京地区地震动的三维有限差分模拟[J]. 中国地震,18(4):356–364. doi: 10.3969/j.issn.1001-4683.2002.04.005 Gao M T,Yu Y X,Zhang X M,Wu J,Hu P,Ding Y H. 2002. Three-dimensional finite-difference simulations of ground motions in the Beijing area[J]. Earthquake Research in China,18(4):356–364 (in Chinese).
贺秋梅. 2012. 地震动的速度脉冲对结构反应及结构减隔震性能影响研究[D]. 北京: 中国地震局地球物理研究所: 1−10. He Q M. 2012. Study on the Influence of Seismic Velocity Pulse on Structural Response and Isolation Properties[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 1−10 （in Chinese）.
姜慧,黄剑涛,俞言祥,温增平. 2009. 地表破裂断层近场速度大脉冲研究[J]. 华南地震,29(2):1–9. doi: 10.3969/j.issn.1001-8662.2009.02.001 Jiang H,Huang J T,Yu Y X,Wen Z P. 2009. Study on large velocity pulses near surface rupture faults[J]. South China Journal of Seismology,29(2):1–9 (in Chinese).
李晓轩. 2016. 速度脉冲提取与夹杂对地震动的影响研究[D]. 哈尔滨: 中国地震局工程力学研究所: 10−11. Li X X. 2016. Study on Extraction of the Velocity Pulse and Effects of Inclusion on Ground Motion[D]. Harbin: Institute of Engi-neering Mechanics, China Earthquake Administration: 10−11 （in Chinese）.
李宗超,高孟潭,陈学良,吴清. 2019. 2016年熊本MJ7.3地震的工程地震动参数模拟及分布特征分析[J]. 地震学报,41(1):100–110. Li Z C,Gao M T,Chen X L,Wu Q. 2019. Engineering ground motion parameters simulation and distribution characteristics analysis of Kumamoto MJ7.3 earthquake in 2016[J]. Acta Seismologica Sinica,41(1):100–110 (in Chinese).
刘启方,袁一凡,金星,丁海平. 2006. 近断层地震动的基本特征[J]. 地震工程与工程振动,26(1):1–10. doi: 10.3969/j.issn.1000-1301.2006.01.001 Liu Q F,Yuan Y F,Jin X,Ding H P. 2006. Basic characteristics of near-fault ground motion[J]. Earthquake Engineering and Engineering Vibration,26(1):1–10 (in Chinese).
罗全波,陈学良,高孟潭,李宗超,李铁飞,张振. 2018. 近断层速度脉冲与震源机制的关系浅析[J]. 震灾防御技术,13(3):646–661. Luo Q B,Chen X L,Gao M T,Li Z C,Li T F,Zhang Z. 2018. Relationship between near-fault velocity pulse and focal mecha-nism[J]. Technology for Earthquake Disaster Prevention,13(3):646–661 (in Chinese).
潘波,许建东,关口春子,何宏林. 2006. 北京地区近断层强地震动模拟[J]. 地震地质,28(4):623–634. doi: 10.3969/j.issn.0253-4967.2006.04.010 Pan B,Xu J D,Haruko S,He H L. 2006. Simulation of the near-fault strong ground motion in Beijing region[J]. Seismology and Geology,28(4):623–634 (in Chinese).
蒲武川,梁瑞军,戴枫禹,黄斌. 2017. 基于三角函数的脉冲型近场地震动的近似模型[J]. 振动与冲击,36(4):208–213. Pu W C,Liang R J,Dai F Y,Huang B. 2017. An analytical model for approximating pulse-like near-fault ground motions[J]. Journal of Vibration and Shock,36(4):208–213 (in Chinese).
王海云. 2004. 近场强地震动预测的有限断层震源模型[D]. 哈尔滨: 中国地震局工程力学研究所: 39−64. Wang H Y. 2004. Finite Fault Source Model for Predicting Near-Field Strong Ground Motion[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration: 39−64 （in Chinese）.
王卫民,赵连锋,李娟,姚振兴. 2005. 1999年台湾集集地震震源破裂过程[J]. 地球物理学报,48(1):132–147. doi: 10.3321/j.issn:0001-5733.2005.01.019 Wang W M,Zhao L F,Li J,Yao Z X. 2005. Rupture process of the Chi-Chi (Taiwan)earthquake in 1999[J]. Chinese Journal of Geophysics,48(1):132–147 (in Chinese).
谢俊举,温增平,李小军,李亚琦,吕红山,黄隽彦. 2012. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性[J]. 地球物理学报,55(6):1963–1972. Xie J J,Wen Z P,Li X J,Li Y Q,Lü H S,Huang J Y. 2012. Analysis of velocity pulses for near-fault strong motions from the Wenchuan earthquake based on wavelet method[J]. Chinese Journal of Geophysics,55(6):1963–1972 (in Chinese).
徐龙军,谢礼立. 2005. 集集地震近断层地震动频谱特性[J]. 地震学报,27(6):656–665. doi: 10.3321/j.issn:0253-3782.2005.06.010 Xu L J,Xie L L. 2005. Characteristics of frequency content of near-fault ground motions during the Chi-Chi earthquake[J]. Acta Seismologica Sinica,27(6):656–665 (in Chinese).
俞言祥,高孟潭. 2001. 台湾集集地震近场地震动的上盘效应[J]. 地震学报,23(6):615–621. doi: 10.3321/j.issn:0253-3782.2001.06.007 Yu Y X,Gao M T. 2001. Effects of the hanging wall and footwall on peak acceleration during the Chi-Chi earthquake,Taiwan[J]. Acta Seismologica Sinica,23(6):615–621 (in Chinese).
袁一凡, 田启文. 2012. 工程地震学[M]. 北京: 地震出版社: 128−138. Yuan Y F, Tian Q W. 2012. Engineering Seismology[M]. Beijing: Seismological Press: 128−138 （in Chinese）.
Baker J W. 2007. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bull Seismol Soc Am,97(5):1486–1501. doi: 10.1785/0120060255
Benioff H. 1955. Mechanism and strain characteristics of the White Wolf fault as indicated by the aftershock sequence,earthquakes in Kern County,California during 1955[J]. Calif Div Mines Bull,171:199–202.
Bray J D,Rodriguez-Marek A. 2004. Characterization of forward-directivity ground motions in the near-fault region[J]. Soil Dyn Earthq Eng,24(11):815–828. doi: 10.1016/j.soildyn.2004.05.001
Carena S,Suppe J,Kao H. 2002. Active detachment of Taiwan illuminated by small earthquakes and its control of first-order topography[J]. Geology,30(10):935–938. doi: 10.1130/0091-7613(2002)030<0935:ADOTIB>2.0.CO;2
Cattin R,Loevenbruck A,Le Pichon X. 2004. Why does the co-seismic slip of the 1999 Chi-Chi (Taiwan)earthquake increase progressively northwestward on the plane of rupture? [J]. Tectonophysics,386(1/2):67–80.
Chen C H,Teng T L,Gung Y C. 1998. Ten-second Love-wave propagation and strong ground motions in Taiwan[J]. J Geophys Res,103(B9):21253–21273. doi: 10.1029/98JB00613
Chen R Y,Kao H,Liang W T,Shin T C,Tsai Y B,Huang B S. 2009. Three-dimensional patterns of seismic deformation in the Taiwan region with special implication from the 1999 Chi-Chi earthquake sequence[J]. Tectonophysics,466(3/4):140–151.
Chi W C,Dreger D,Kaverina A. 2001. Finite-source modeling of the 1999 Taiwan (Chi-Chi)earthquake derived from a dense strong-motion network[J]. Bull Seismol Soc Am,91(5):1144–1157.
Dickinson B W,Gavin H P. 2011. Parametric statistical generalization of uniform-hazard earthquake ground motions[J]. J Struct Eng,137(3):410–422. doi: 10.1061/(ASCE)ST.1943-541X.0000330
Hanks T C,Kanamori H. 1979. A moment magnitude scale[J]. J Geophys Res,84(B5):2348–2350. doi: 10.1029/JB084iB05p02348
Heaton T H,Hall J F,Wald D J,Halling M W. 1995. Response of high-rise and base-isolated buildings to a hypothetical MW7.0 blind thrust earthquake[J]. Science,267(5195):206–211. doi: 10.1126/science.267.5195.206
Hirasawa T,Stauder W. 1965. On the seismic body waves from a finite moving source[J]. Bull Seismol Soc Am,55:237–262.
Irikura K,Miyakoshi K,Kamae K,Yoshida K,Somei K,Kurahashi S,Miyake H. 2017. Applicability of source scaling relations for crustal earthquakes to estimation of the ground motions of the 2016 Kumamoto earthquake[J]. Earth Planets Space,69(1):10. doi: 10.1186/s40623-016-0586-y
Iwaki A,Morikawa N,Maeda T,Aoi S,Fujiwara H. 2013. Finite-difference simulation of long-period ground motion for the Sagami Trough megathrust earthquakes[J]. J Disaster Res,8(5):926–940. doi: 10.20965/jdr.2013.p0926
Kawase H,Aki K. 1990. Topography effect at the critical SV-wave incidence:Possible explanation of damage pattern by the Whittier Narrows,California,earthquake of 1 October 1987[J]. Bull Seismol Soc Am,80(1):1–22.
Li Z C,Gao M T,Jiang H,Chen X L,Li T F,Zhao X F. 2018. Sensitivity analysis study of the source parameter uncertainty factors for predicting near-field strong ground motion[J]. Acta Geophys,66(4):523–540. doi: 10.1007/s11600-018-0171-9
Luo Q B,Chen X L,Gao M T,Li Z C,Zhang Z,Zhou D. 2019. Simulating the near-fault large velocity pulses of the Chi-Chi (MW7.6) earthquake with kinematic model[J]. J Seismol,23(1):25–38. doi: 10.1007/s10950-018-9791-4
Ma K F,Wang J H,Zhao D P. 1996. Three-dimensional seismic velocity structure of the crust and uppermost mantle beneath Taiwan[J]. J Phys Earth,44(2):85–105. doi: 10.4294/jpe1952.44.85
Murotani S,Miyake H,Koketsu K. 2008. Scaling of characterized slip models for plate-boundary earthquakes[J]. Earth Planets Space,60(9):987–991. doi: 10.1186/BF03352855
Oglesby D D,Archuleta R J. 1997. A faulting model for the 1992 Petrolia earthquake:Can extreme ground acceleration be a source effect? [J]. J Geophys Res,102(B6):11877–11897. doi: 10.1029/97JB00475
Somerville P,Irikura K,Graves R,Sawada S,Wald D,Abrahamson N,Iwasaki Y,Kagawa T,Smith N,Kowada N. 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J]. Seismol Res Lett,70(1):59–80. doi: 10.1785/gssrl.70.1.59
Wang C Y,Chang C H,Yen H Y. 2000. An interpretation of the 1999 Chi-Chi earthquake in Taiwan based on the thin-skinned thrust model[J]. Terr Atmos Ocean Sci,11(3):609–630. doi: 10.3319/TAO.2000.11.3.609(CCE)
Wells D L,Coppersmith K J. 1994. New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J]. Bull Seismol Soc Am,84(4):974–1002.
-
期刊类型引用(6)
1. 刘文玉，程正璞，年秀清，陈闫，胡钰铃，覃祖建，邵明正. 基于三维剩余密度结构的松原地震成因. 地震地质. 2024(02): 462-476 . 
百度学术
2. 张仁鹏，雷焕珍，陈聪，陈琳荣，冯靖乔. 2019年松原M_S5.1地震烈度评定及震害特征简析. 防灾减灾学报. 2023(01): 34-40 . 百度学术
3. 于晨，卢军，解滔，刘长生. 2017—2019年松原地区4次中强地震前绥化台地电阻率异常分析. 中国地震. 2023(02): 314-324 . 百度学术
4. 张仁鹏，冯靖乔，雷焕珍，于宏伟，马飞，王佳蕾. 松原市5.7级和5.1级地震房屋震害特征分析与启示. 防灾科技学院学报. 2022(03): 80-87 . 百度学术
5. 李梦莹，张志宏，焦明若，方禹心. 2018-05-28松原M_S5.7地震地电场变化特征研究. 大地测量与地球动力学. 2022(12): 1276-1280+1299 . 百度学术
6. 李梦莹，杨士超，张志宏，孔祥瑞，孙庆山. 2018年松原M_S 5.7地震地电场变化特征. 地震地磁观测与研究. 2022(S1): 120-122 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1916
- HTML全文浏览量: 1046
- PDF下载量: 72
- 被引次数: 8
