Remote triggering of non-volcanic tremor in southern Taiwan
-
摘要: 选取2011—2016年发生的38次震中距大于1 000 km的MW≥7.5地震震后3小时的连续波形资料，利用人工检视方法对这38次地震是否触发了我国台湾地区的非火山型微震颤进行了调查。分析结果显示：这38次地震中有4次远震触发了非火山型微震颤，事件持续300—500 s不等。利用网格搜寻方法对此4次微震颤事件进行了定位，确定震中位于台湾中央山脉南段，震源深度为21—53 km。结合研究区内地球物理观测资料，分析认为是由于远震产生的面波改变了研究区内的瞬时应力，进而导致断层蠕滑触发了微震颤事件。Abstract: We selected three-hour continuous waveforms after 38 MW≥7.5 earthquakes with epicentral distance larger than 1 000 km during 2011 to 2016 in Taiwan region of China to investigate whether it has triggered non-volcanic tremors （NVTs） by using visual identification. Out of the 38 earthquakes, we identified four teleseismic events which triggered NVTs with duration ranging from 300 s to 500 s. Using grid search, four tremor sources were located in the southern Central Range in Taiwan and the focal depth ranges from 21 to 53 km. Based on the local geophysical observation data, we proposed that the transient stress change induced by surface wave of large teleseisms could lead to the fault creep, which is the critical factor for tremor generation.
-
Keywords:
- non-volcanic tremor /
- dynamic stress /
- surface wave triggering /
- Taiwan region
-
引言
随着国民经济的飞速发展，当今社会对清洁能源的需求量不断扩大，常规能源逐渐耗竭，深部、非常规能源（例如：页岩气、煤层气、地热等）的开发与发展逐渐兴起（邹才能等，2016，2017；管全中等，2021）。深部能源的开采普遍采用高压注水的方式，这种方式虽然能够明显地提高油气井、地热井的单井产出量，达到增产效果，但是近年来的大量研究表明，注水开采深部能源会引发大量的有感地震。例如：2016年美国波尼MW5.8地震（Walter et al，2017）、2017年韩国浦项MW5.5地震（Chang et al，2020；Yeo et al，2020）、2019年四川长宁MS6.0地震震群（易桂喜等，2019；Lei et al，2019a，b，2020；Liu，Zahradnik，2020；李大虎等，2021；Li et al，2021）等。
已有的研究表明，地震的诱因是压裂流体的注入导致储层内部压力产生变化，引发断层的失稳滑移（涂毅敏，陈运泰，2002；张致伟等，2012；Ellsworth，2013；朱航，何畅，2014；Keranen et al，2014；Rubinstein et al，2018；Meng et al，2019）。断层的滑动形式与压力的变化密切相关，蠕滑和粘滑的滑动形式又将左右地震的发生与否（Brace，Byerlee，1966；Jaeger，Cook，1969；洪汉净，1994；周仕勇，2008；薛霆虓等，2009）。因此，判断断层的滑动形式是探究注水诱发地震问题首要应该探明的机理。
控制流体注入速度可以降低诱发地震的发生几率（Alghannam，Juanes，2020）。例如，与高流速注入井相比，低流速注入井诱发地震的可能性要小很多（Frohlich，2012；Keranen et al；Langenbruch，Zoback，2016；Keranen，Weingarten，2018），这种现象说明诱发地震的流速临界值与储层的性质密切相关。另外，流体注入速率变化的时间与地震的发生同样密切相关（Weingarten et al，2015；Goebel，Brodsky，2018；Rubinstein et al，2018）。地震往往发生在注入速率突增的时刻（Yeo et al，2020；Rajesh，Gupta，2021），或者是发生在突然停止注入的时刻（Goebel et al，2017，2019）。虽然大量研究人员已经尝试通过建立多种二维地质模型来解释一些现场观测结果（Cueto-Felgueroso et al，2017；Jin，Zoback，2018；Norbeck，Horne，2018；Andrés et al，2019；Zhu et al，2020），但是对于流体注入方式与诱发地震产生的物理机制仍然知之甚少。
此外，摩擦滑动的稳定性与断层面的地震成核过程直接相关（Dieterich，1992；Dieterich et al，2015；Cappa et al，2019）。相关科研人员使用准稳态法（Lick，1965；Robinson，1976；Segel，Slemrod，1989；Rao，Arkin，2003），并借助于孔弹性弹簧-滑块模型，分析注水作用下断层的稳定性条件（Alghannam，Juanes，2020）。但上述的研究仍然存在一些不足：① 现有的研究大多集中在二维地质模型的尺度上，不能如实地反应真实地质条件；② 现有的稳定性条件仅仅考虑了有效应力的影响，而忽略了有效应力（注水压力）变化率的影响；③ 在进行稳定性计算时，对于流体压力的计算多数为解析解，忽略了流固耦合过程。
因此，本文首先建立孔弹性力学耦合模型，研究在三种典型的注水方式（上升型、迅速上升/下降型和间歇型）下断层的动力响应情况，并采用孔弹性弹簧-滑块模型对断层的稳定性进行分析，研究了注水速率与储层渗透性对断层的临界刚度的影响，分析断层可能发生不稳定滑动的条件，进而为工业注采能够安全生产的进行提供定量的参考依据。
1. 数学模型
1.1 孔弹性力学耦合数学模型
多孔弹性的线性理论最早由Biot （1941）提出，其变形控制方程为
$$ G{u}_{i{\text{，}}kk}{\text{＋}}\frac{G}{1-2v}{u}_{k{\text{，}}ki}{\text{＝}}{f}_{i}{\text{＋}}{\alpha }_{{\rm{f}}}{p}_{{\rm{f}}} {\text{，}} $$ (1) 式中，u为位移，pf为流体压力，αf为Biot系数，v为泊松比，G为剪切模量，下标i和k代表变量u的三个方向的分量，其中i，k＝1，2，3，下标kk是爱因斯坦求和约定，逗号代表对变量的求导。
流体的质量平衡方程主要包含流体质量的变化率mf、流体的质量通量Jf和质量源项Qs，且有
$$ \frac{ {\text{∂}} {m}_{{\rm{f}}}}{{\text{∂}} t}{\text{＋}}\nabla \cdot {J}_{{\rm{f}}}{\text{＝}}{Q}_{{\rm{s}}} {\text{，}} $$ (2) 耦合模型中，流体质量变化与流体压力变化和变形相关，即
$$ \frac{{\text{∂}} {m}_{{\rm{f}}}}{{\text{∂}} t}{\text{＝}}\frac{{\text{∂}} {\rho }_{{\rm{f}}}{\varphi }_{{\rm{f}}}}{{\text{∂}} t}{\text{＝}}{\rho }_{{\rm{f}}}{S}_{{\rm{f}}}\frac{{\text{∂}} {p}_{{\rm{f}}}}{{\text{∂}} t}{\text{＋}}{{\rho }_{{\rm{f}}}\alpha }_{{\rm{f}}}\frac{{\text{∂}} {\varepsilon}_{{\rm{v}}}}{{\text{∂}} t} $$ (3) 式中，φf为储层的孔隙率，ρf为储层中的流体密度，εv为体积应变，储水系数Sf＝φfCf＋（1－φf）Cm，其中Cf和Cm分别为流体和固体骨架的压缩系数。
流体质量通量Jf可以表示为
$$ {J}_{{\rm{f}}}{\text{＝}}-\frac{{\kappa }_{{\rm{f}}}}{{\mu }_{{\rm{f}}}}{\rho }_{{\rm{f}}}{\text{（}}\nabla {p}_{{\rm{f}}}{\text{＋}}{\rho }_{{\rm{f}}}g{\text{）}} {\text{，}} $$ (4) 式中，κf为储层中的渗透率，μf为流体动态粘度系数，g为重力加速度。
耦合两相流模型应用COMSOL Multiphysics求解器进行耦合计算。采用达西模块中的储水模型计算注水过程，采用固体力学模块计算注水引起的储层变形，孔隙弹性力学耦合过程通过变形控制方程中的
$ {\alpha }_{{\rm{f}}}{p}_{{\rm{f}}} $ 和渗流扩散方程中的$ \;{{\rho }_{{\rm{f}}}\alpha }_{{\rm{f}}}\dfrac{{\text{∂}} {\varepsilon}_{{\rm{v}}}}{{\text{∂}} t} $ 来实现（Rice，Cleary，1976；Wang，2000；Cheng et al，2012，2016；Segall，Lu，2015）。1.2 孔弹性弹簧-滑块模型
当流体注入储层后，流体压力的变化会引起储层及断层中有效应力的变化。孔弹性弹簧-滑块模型（图1）是由弹簧和滑块组成，弹簧末端施加恒定的滑移速率v0，滑块的滑移速度为v，滑块所受到的剪应力为τ，p0表示模型的参考流体压力，q表示流体注入速度，p表示流体注入后流体压力，w表示活塞垂直方向伸长量。该模型可以很好地解释沿断层的剪切应力与有效正应力之间的流体弹性耦合问题。
![]()
图 1 孔弹性弹簧-滑块模型示意图（引自Alghannam，Juanes，2020）Figure 1. Schematic diagram of poroelastic spring–slider model （after Alghannam，Juanes，2020）摩擦系数演化采用速率-状态的本构方程来表示，该方程能够准确地描述断层滑移引起的地震行为，从震前滑移和地震成核到同震破裂和震后滑移。该方程表明了摩擦剪应力是有效正应力和摩擦系数的函数，并依赖于滑移速率和滑动面的状态，方程可以写为（Ruina，1983；Scholz，2002）
$$ \mu {\text{＝}}{\mu }_{*}{\text{＋}}a\mathit{{\rm{ln}}}\left(\frac{v}{{v}_{*}}\right){\text{＋}}\varTheta {\text{，}} $$ (5) 式中：Θ为滑块滑动状态函数；a为稳态速度依赖性参数，与滑块摩擦系数变化相关，可以从实验中得到；下标*代表参考状态值。如果考虑有效应力的变化，则Θ为
$$ \dot{\varTheta }{\text{＝}}-\frac{v}{{D}_{{\rm{c}}}}\Bigg(\varTheta {\text{＋}}b\mathit{{\rm{ln}}}\frac{v}{{v}_{*}}\Bigg){\text{－}}\hat{\alpha}\frac{{\dot{\sigma }}_{{\rm{e}}}}{{\sigma }_{{\rm{e}}}} {\text{，}} $$ (6) 式中：Dc为特征滑移距离；b为摩擦本构参数，可以通过实验测得；
$\hat{\alpha} $ 为比例因子，其取值从0到μ；$ {\sigma }_{{\rm{e}}} $ 为有效应力，可以写为$ {\sigma }_{{\rm{e}}}{\text{＝}}\sigma {\text{－}}{p}_{{\rm{f}}} $ ；“·”代表变量对时间求导。式（5）和（6）共同构成了摩擦本构方程。1.3 线性稳定性分析
摩擦滑动的稳定性与断层面上的地震成核过程相关，假设系统发生一个小扰动，如果摩擦强度随着该扰动发生微小的变化且很快恢复，那么这样的系统是稳定的。如果这个系统渐渐脱离稳态，系统是不稳定的。对孔弹性弹簧-滑块系统的运动过程进行描述（Alghannam，Juanes，2020），可以得到
$$ \dot{U}{\text{＝}}{v}_{0}{\text{－}}v {\text{，}} $$ (7) $$ {\left(\frac{2\pi}{T} \right)^{2}}\Bigg[U{\text{－}}\frac{1}{{\kappa }_{{\rm{s}}}}\Bigg({\mu }_{*}{\text{＋}}a\mathit{{\rm{ln}}}\frac{v}{{v}_{*}}{\text{＋}}\varTheta \Bigg){\text{（}}\sigma {\text{－}}{p}_{{\rm{f}}}{\text{）}}\Bigg] {\text{＝}}0{\text{，}}$$ (8) $$ \dot{\varTheta }{\text{＝}}-\frac{v}{{D}_{{\rm{c}}}}\Bigg(\varTheta {\text{＋}}b\mathit{{\rm{ln}}}\frac{v}{{v}_{*}}\Bigg){\text{＋}}\hat{\alpha}\frac{{\dot{p}}_{{\rm{f}}}}{\sigma {\text{－}}{p}_{{\rm{f}}}} {\text{，}} $$ (9) 式中，U代表系统位移，κs为系统刚度，
$ T{\text{＝}}2\pi \sqrt{m/{\kappa }_{{\rm{s}}}} $ 为系统的自由振动周期。对上述方程，在准稳态值vqss＝v0和$ \varTheta {\text{＝}}\hat{\alpha}{\dot{p}}_{{\rm{f}}}/\sigma {\text{－}}{p}_{{\rm{f}}}/{v}_{0}{\text{－}}b{{\rm{ln}}v}_{0} $ 附近进行线性展开和时间求导，可以得到$$ \Delta \dot{v}{\text{＝}}\frac{{v}_{0}}{a}\Bigg[\frac{b}{{D}_{{\rm{c}}}}{\text{＋}}\frac{\hat{\alpha}}{{v}_{0}}\frac{{\dot{p}}_{{\rm{f}}}}{\sigma {\text{－}}{p}_{{\rm{f}}}}{\text{－}}\frac{{\kappa }_{{\rm{s}}}}{\sigma {\text{－}}{p}_{{\rm{f}}}}\Bigg]\Delta v{\text{＋}}\frac{{{v}^{2}_{0}}}{a}\Delta \varTheta {\text{，}} $$ (10) $$ \Delta \dot{\varTheta }{\text{＝}}-\Bigg[\frac{b}{{D}_{{\rm{c}}}}{\text{＋}}\frac{\hat{\alpha}}{{v}_{0}}\frac{{\dot{p}}_{{\rm{f}}}}{\sigma {\text{－}}{p}_{{\rm{f}}}}\Bigg]\Delta v{\text{－}}\frac{{v}_{0}}{{D}_{{\rm{c}}}}\Delta \varTheta {\text{，}} $$ (11) 式（10）和（11）为2×2阶常微分方程组，其通解形式为
$ \Delta v{\text{＝}}V{{\rm{e}}}^{\lambda t} $ 和$ \Delta \varTheta {\text{＝}}\varTheta {{\rm{e}}}^{\lambda t} $ 。将两个通解代入到上式中，可以得到特征方程为$$ a{\text{（}}\sigma {\text{－}}{p}_{{\rm{f}}}{\text{）}}{\lambda }^{2}{\text{＋}}{\text{（}}-\hat{\alpha}{\dot{p}}_{{\rm{f}}}{\text{＋}}{\kappa }_{{\rm{s}}}{v}_{0}{\text{－}}(b{\text{－}}a{\text{）}}{\text{（}}\sigma {\text{－}}{p}_{{\rm{f}}}{\text{）}}{v}_{0}{\text{）}}\lambda {\text{＋}}{\kappa }_{{\rm{s}}}{{v}^{2}_{0}}{\text{＝}}0 {\text{.}} $$ (12) 针对于上述方程，如果根λi的实部均为负值，则系统是稳定的；如果根λi的实部存在正值，则系统是不稳定的。因此我们可以得到注水过程中的系统刚度的临界值，即
$$ {\kappa }_{{\rm{crit}}}{\text{＝}}\frac{{\text{（}}b{\text{－}}a{\text{）}}}{{D}_{{\rm{c}}}}{\text{（}}\sigma {\text{－}}{p}_{{\rm{f}}}{\text{）}}{\text{＋}}\frac{\hat{\alpha}}{{v}_{0}}{\dot{p}}_{{\rm{f}}} {\text{.}} $$ (13) 对于速度强化情况（a－b＞0），系统刚度κs总是大于临界刚度κcrit，系统总是稳定的。对于速度弱化情况（a－b＜0），系统的稳定性与κs和κcrit的大小有关，当κs＜κcrit，系统在微小的扰动下，容易发生不稳定的粘滑；当κs=κcrit时，系统表现为周期性的振荡；当κs＞κcrit时，系统为稳定的滑动（Ruina，1983）。本文考虑的是速度弱化下的情况，从式（13）可以看出，系统的临界刚度与流体压力和流体压力的变化率相关。临界刚度随着流体压力的上升而下降，断层比较容易形成稳定滑动，不易诱发地震；随着流体压力变化率的上升而上升，容易引起断层的不稳定滑动，容易引起地震。本文采用式（13）分析了不同注水方式、不同渗透率对于临界刚度的影响，从而进一步判断注水导致的断层的滑动是危险的粘滑还是稳定的蠕滑。
2. 数值模型
2.1 三维地质模型
由于本文重点关注注水方式对断层动力学响应，因此本文建立的三维地质模型（图2），长、宽、高均设定为1 000 m。其中，储层位于地质模型中间层，高度设定为60 m。注入流体以垂直井的方式注入，井位于储层中间位置。断层长度约为400 m，厚度约为10 m，其中心点与注水井的距离约为300 m，断层与水平方向倾角设为45°，如图2a所示。采用自由四边形对计算区域进行网格划分，在注水井处和断层处对网格进行加密，如图2b所示，进行网格划分后，共有网格112 063个，平均网格质量为0.764 2。
![]()
图 2 研究区几何模型（a）和网格划分示意图（b）Figure 2. Geometric model （a） and meshing schematic diagram （b） of the studied area2.2 模型参数和边界条件
储层渗透率、孔隙度、弹性模量和泊松比分别设置为κf＝10−14 m2，ϕf＝0.1，E＝20 GPa，v＝0.25。流体密度、动态粘度和压缩系数分别为ρf＝1 000 kg/m3，uf＝0.001 Pa·s和Cf＝4×10−10 Pa−1。上部盖层和底部基岩的渗透约为储层的1/10 000，断层渗透率约为10−13 m2。对于流固耦合因子，Biot系数设置为一个常数αf＝1。
对于固体力学边界条件，底端固定，水平应力σx＝80 MPa，σy＝100 MPa。对于流体流动，初始参考流体压力p0为0.1 MPa。流体从垂直井注入，其余边界为无流动边界。对于计算参数，我们选取a＝0.015，b＝0.02，Dc＝100 μm，
$ \hat \alpha $ ＝0.5。本项目中所采用的参数列于表1。表 1 模型材料参数Table 1. The material parameters of the model变量 含义 值 变量 含义 值 ρf 流体密度 1 000 kg/m3 uf 流体动态粘度系数 0.001 Pa·s Cf 流体压缩系数 4×10−10 Pa−1 κf 储层渗透率 10−14 m2 ϕf 储层孔隙率 0.1 E 储层弹性模量 20 GPa v 储层泊松比 0.25 αb Biot系数 1 σ y y方向应力 100 MPa σx x方向应力 80 MPa a 摩擦常数 0.015 b 摩擦常数 0.02 Dc 滑移距离 100 μm $ \hat \alpha $ 摩擦常数 0.5 p0 参考流体压力 0.1 MPa 2.3 流体注入方式
本文重点研究了三类注水方式，第一种方式（方案A）为注水流量短时间内迅速上升并且流量基本保持不变；第二种方式为上升-下降型（方案B），注水流量在短时间内迅速上升且持续时间约为1.5天，之后迅速下降并保持不变；第三种方式为间歇型（方案C）注水5天，停5天，如此循环。三种注水方式流量变化如图3所示，在注水后第23天，三种方案下的注水体积相同。
![]()
图 3 不同注水方式下注水体积与注水时间的关系曲线Figure 3. The relationship between injection volume and injection time under different water injection schedules方案A的注水体积随注水时间发生线性变化，曲线的斜率为注水流量值。方案B的注水体积随注水时间线性变化且可分为两个阶段：快速增加阶段和缓慢增加阶段。方案C的注水体积随注水时间线性变化且分若干个循环，每个循环分为增加阶段和恒定阶段。在注水前期，方案B的注水体积增长速率远大于方案A和方案C，且随注水时间的增加，方案B的注水体积与方案A、方案C的注水体积的差值越来越大。随着方案B中注水流量的大幅度降低且小于方案A和方案C的注水流量，方案B进入缓慢增加阶段。该阶段方案B的注水体积增长速率小于方案A和方案C，使得随着注水时间的增加，方案B的注水体积与方案A、方案C的注水体积的差值越来越小，在注水后第23天，三种方案下的注水体积相同。方案A与方案C相比，两者注水体积差别不大，在方案C的增加阶段，其注水总体积大于方案A，在恒定阶段，方案A的注水总体积大于方案C。其中本系统的初始刚度约为7×109 N/m。
3. 结果分析与讨论
3.1 注水压力变化
本文分析了三种不同注水方案条件下，断层中部、上部及下部流体压力随时间的变化关系（图4）。在不同注水方式下，断层不同位置处的流体压力产生了一定的差异，这与注水后流体在岩体内的流动路径相关。由于注水井在储层内部，流体首先被注入储层内及与储层相连的断层内部，引起了断层中部的流体压力的增大。随着注水的持续，水不断向外渗透。在重力作用下，水向断层下部渗透难度小于向断层上部渗透。因此，断层流体压力增大的时间顺序为，断层中部最先变化，断层下部次之，断层上部最晚。
![]()
图 4 不同注水方式下，断层上部、中部及下部流体压力与注水时间的关系曲线Figure 4. The liquid pressure in the middle, upper and lowerparts of the fault under different water injection schedules对比三种注水方案下引起的流体压力变化，可以发现，断层内流体压力变化与流体注入方式紧密相关，方案A流体压力呈现缓慢增长阶段和线性增长阶段，在注水前期（0—5天），流体压力缓慢增长，此时注入流体还未完全影响断层；在线性增长阶段，流体压力已经完全进入断层内。方案B下不同位置流体压力变化曲线分为两个阶段，快速增长阶段和稳定增长阶段。与方案A相比，快速增长阶段是由于方案B中注水初期较高的注水流量导致的。方案C下断层流体压力的变化则较为复杂，流体压力可以分为若干个循坏，每个循环包括快速增长阶段和缓慢增长阶段，缓慢增长阶段发生在流体停止注入阶段，主要是由储层内的流体向断层扩散导致。
3.2 渗透率对注水压力的影响
本文对比分析了不同注水方案、不同渗透率（5κf，κf，0.2κf）下储层和断层流体压力变化。从图5可以看出，在三种不同的注水方式下，储层平均流体压力均大于断层平均流体压力，随着渗透率的增大储层平均流体压力与断层平均流体压力的差值不断减小。在相同的注水方式下，渗透率越小，储层流体压力越大，断层流体压力越小，储层平均流体压力与断层平均流体压力的差值越大。
![]()
图 5 不同注水方式和不同渗透率下流体压力在储层（a）和断层（b）中随时间的变化Figure 5. Liquid pressure changes with time in reservoir （a） and fault （b） under different permeabilities and water injection schedules方案B中储层平均压力曲线出现了水力压力峰值，但在断层储层平均压力曲线中没有出现。这是由于在前期较大注水流量下，水没有及时向外渗流，导致在注水井附近储层内大量积水，该区域内产生较大的流体压力，且渗透率越小幅值越大。当注水量大幅降低后，随着储层内大量积水不断向外流动，储层内积水不断减少，流体压力下降且渗透率越大，储层平均流体压力下降幅度越大。注水方案C中流体压力所呈现的阶梯式增长方式随着渗透率降低越发不明显，当渗透率取值较小，方案C与方案A所引起的断层流体压力增大趋势基本相同。
3.3 断层临界刚度的变化
对比分析三种注水方案下，断层上、中、下部临界刚度随时间变化的规律。由于方案A与方案C的临界刚度数值比较接近且与方案B的临界刚度数值差距较大，因此分别由图6a和图6b表示。从图中可以看出，在三种不同的注水方式下，断层临界刚度与流体压力变化类似，断层中部临界刚度首先发生变化，且增值最大。
![]()
图 6 方案A，C （a）和方案B （b）的断层临界刚度随时间的变化Figure 6. The fault critical stiffness changes with time under cases A，C （a） and case B （b）在方案A中，断层不同位置处的断层刚度随注水时间的增加，均呈现出了先快速增加后缓慢降低的趋势。在方案B中，断层不同位置的刚度随注水时间的增加均呈现出快速增加、快速降低和缓慢降低三个阶段。在方案C中，断层不同位置处的临界刚度呈现循环变化，每个循环可以分为快速增加、快速降低和缓慢降低三个阶段。
与此同时，我们对比了三种不同注水方式下断层临界刚度的变化。如图6所示，在注水初期，方案B的断层刚度明显大于方案A和方案C的断层刚度。在注水时间为1.3天时，方案B的断层临界刚度达到峰值，且为方案A的2.8倍，为方案C的断层刚度值的2.5倍。随着注水时间的增加，方案B的断层刚度进入快速下降阶段，而方案A的断层刚度仍呈现一段时间的上升趋势。方案C的断层刚度变化则呈现出循环变化，循环周期约为10天。方案C的每个循环周期内断层刚度均在中间时段达到峰值，并随着循环次数的增加呈现降低趋势。
由上述分析可知，在注水早期，相比方案A和方案C，方案B更容易发生不稳定滑动。在注水后期，在方案C的一个刚度循环时间内，方案C比方案A和方案B更容易引起断层的不稳定粘滑。
由式（13）可知，断层的临界刚度是由断层流体压力及流体压力变化率共同决定的，与流体压力变化率正相关，而与流体压力负相关。因此本文给出了三种不同的注水方案下，两者对于断层临界刚度的影响规律，结果如图7所示。
![]()
图 7 方案A，C （a）和方案B （b）在分别考虑流体压力（负半轴）及流体压力变化率（正半轴）时断层临界刚度随时间的变化Figure 7. The critical stiffness changes of fault with time when considering the liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis） respectively for cases A，C （a）and case B （b）对于方案A，流体压力变化率引起的断层刚度变化随着注水时间先增大后保持不变，同时断层内增大的流体压力使临界刚度线性减小，但前者引起的数值增大明显大于后者所引起的数值减小。在二者的共同作用下，断层刚度变化随着注水时间先急剧增大后逐渐下降。
对于方案B，在流体压力的影响下，断层刚度在注水初期快速降低，后变为缓慢降低；流体压力的变化率则先快速增大后快速降低，最后保持不变。在两者共同作用下，断层刚度随着注水时间的增加先快速增大后快速降低，最后保持不变。由此可知，注水前期流体压力变化率对断层刚度影响较大，注水后期流体压力对断层刚度影响较大，两者叠加后临界刚度表现出先快速增大后快速降低，最后呈现缓慢降低趋势。
对于方案C，流体压力和流体压力变化率引起的临界刚度可分为若干个循环，每个循坏内流体压力与流体压力变化率对于临界刚度的影响与注水方案B类似。在流体压力的影响下，断层刚度先快速降低，后变为缓慢降低，流体压力的变化率则先快速增大后快速降低，最后保持不变。但由于注水方案C注入流量较低，引起的增大值明显小于方案B。
3.4 渗透率对断层临界刚度的影响
相似的，我们分析了储层渗透率对于三种注水方案下断层临界刚度的影响。对于方案A （图8），不难看出，渗透率越大，断层刚度响应时间越短。并且如图8b所示，如仅考虑流体压力变化率对断层刚度的影响，则渗透率越大，断层刚度增长越快且率先达到刚度峰值后保持不变；如果仅考虑流体压力对断层刚度的影响，则渗透率越大，断层刚度下降得越快。但不同渗透率对于流体压力变化率的影响要远大于对流体压力的影响。因此，方案A的渗透率越大断层刚度增长速率越大，断层刚度值及峰值越大。随着注水时间的增加，断层刚度进入缓慢下降阶段。该阶段以流体压力变化影响为主，渗透率越大，断层临界刚度下降速率越大，但差异并不明显。
![]()
图 8 方案A中不同渗透率下断层临界刚度随时间的变化（a） 同时考虑流体压力（负半轴）及其变化率（正半轴）；（b） 分别考虑流体压力（负半轴）及其变化率（正半轴）Figure 8. The critical stiffness changes of fault with time under different permeability in case A（a） Considering both of liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis）；（b） Considering liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis） respectively对于方案B （图9），可以看出，渗透率越大，断层刚度响应时间越短。如果仅考虑流体压力变化率对断层刚度的影响（图9b），在快速上升阶段，渗透率越大，断层刚度上升越快且峰值越大；在快速下降阶段，渗透率越大，断层刚度下降越快。如果仅考虑流体压力对断层刚度的影响，渗透率越大断层临界刚度下降越快。综上，方案B在注水前期断层刚度以流体压力变化率影响为主。渗透率越大断层刚度变化速率越大，断层刚度峰值越大。在后期，以流体压力影响为主，渗透率越大断层刚度越小。
![]()
图 9 方案B中不同渗透率下断层临界刚度随时间的变化（a） 同时考虑流体压力（负半轴）及其变化率（正半轴）；（b） 分别考虑流体压力（负半轴）及其变化率（正半轴）Figure 9. The critical stiffness changes of fault with time under different permeability in case B（a） Considering both of liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis）；（b） Considering liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis） respectively对于方案C （图10），可以看出渗透率越大，断层刚度响应时间越短，但渗透率越小，每个循环持续时间越长。在每个循环内，不同渗透率对于临界刚度影响规律与方案B类似。在快速上升阶段，如考虑流体压力变化率的影响，渗透率越大，断层刚度上升越快且峰值越大；在快速下降阶段，渗透率越大，断层刚度下降越快；考虑流体压力对断层刚度的影响，渗透率越大断层临界刚度下降越快。因此，方案C的储层渗透率越大，单个循环持续时间越短。在每个循环前期，断层刚度以流体压力变化率影响为主，渗透率越大断层刚度变化速率越大，断层刚度峰值越大；在后期，以流体压力影响为主，渗透率越大断层刚度越小。
![]()
图 10 方案C中不同渗透率下断层临界刚度随时间的变化（a） 同时考虑流体压力（负半轴）及其变化率（正半轴）；（b） 分别考虑流体压力（负半轴）及其变化率（正半轴）Figure 10. The critical stiffness changes of fault with time under different permeability in case C（a） Considering both of liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis）；（b） Considering liquid pressure （the negative half axis） and liquid pressure change rate （the positive half axis） respectively4. 结论
本文建立了多孔弹性耦合三维有限元模型，基于孔弹性弹簧-滑块模型，研究了三类不同的注水方式（方案A上升型、方案B迅速上升-下降型、方案C间歇型注水型）、不同断层渗透率对断层滑动的影响。经模拟分析得到以下结论：
1） 不同的注水方案下，断层流体压力上升的方式不一样。方案A中的断层流体压力先缓慢上升（此时流体并未到达断层区域），然后稳定上升，此时流体已经达到断层区域。然而对于方案B中的断层流体压力的变化经历两个阶段：迅速上升和稳定上升。其中，迅速上升是由于注水流量迅速上升导致的。方案C中的断层流体压力的变化可以分为若干个循坏，每个循环包括快速增长阶段和缓慢增长阶段，缓慢增长阶段发生在流体停止注入阶段，主要是由于储层内的流体向断层扩散导致。
2） 渗透率的大小影响着储层和断层中流体压力的分布。当渗透率较小时，由于流体在井口处积聚，进而出现了超压现象。在相同的注水方式下，渗透率越小，导致断层流体压力越小，储层平均流体压力与断层平均流体压力的差值越大。
3） 断层的临界刚度的取值与流体压力呈负相关变化，与流体压力的变化率（流体压力对时间导数）呈正相关变化，后者影响较大。在注水前期，流体压力变化率对断层刚度的影响较大，后期流体压力的影响较大。两者叠加后临界刚度表现出先快速增大后降低。在注水初期，方案B的断层临界刚度显著上升，其数值远远大于方案A和方案C，增加了诱发地震的可能性，随后临界刚度迅速下降，在后期，方案C所引起的临界刚度变化值较大。
4） 渗透率的大小对于临界刚度同样有着显著的影响。渗透率越大，断层临界刚度响应时间越短，且变化速率越大，峰值越大。随着注水时间的增加，断层临界刚度进入下降阶段，此时以流体压力影响为主，渗透率越大，断层刚度下降速度越快。
本文给出的孔弹性耦合模型，速率-状态摩擦本构方程和全耦合数值模拟方法，能很好地对断层进行危险性分析，上述模拟结果能为注水诱发地震的危险性评价提供定量的指导意见。但同时本文也存在一些不足之处。首先，假设储层和断层为均质的，这与实际条件并不相符。因为深部致密、非常规储层为沉积储层，一般表现出较强的各向异性特征。其次，由于本文重点关注注水方式对断层动力学响应，因此对于模型的大小、断层的分布、注射井的位置以及应力差等的影响都没有考虑。另外，本文没有考虑在注水压裂过程中孔隙度和渗透率会随着压力的变化而变化。在今后的研究工作中，将继续完善模型，尤其是考虑压裂过程中地层的孔隙度和渗透率变化（Xu，Yu，2008）。同时，将结合实际的工业注水实验与地震精定位数据，研究页岩气开采及干热岩注采诱发地震的成因机理。
感谢中国地震局地球物理研究所吴庆举研究员对本文的撰写进行了指导并提出了有效的建议，两位匿名评审专家在审稿过程中提出了宝贵的意见，作者在此一并表示感谢。
-
![]()
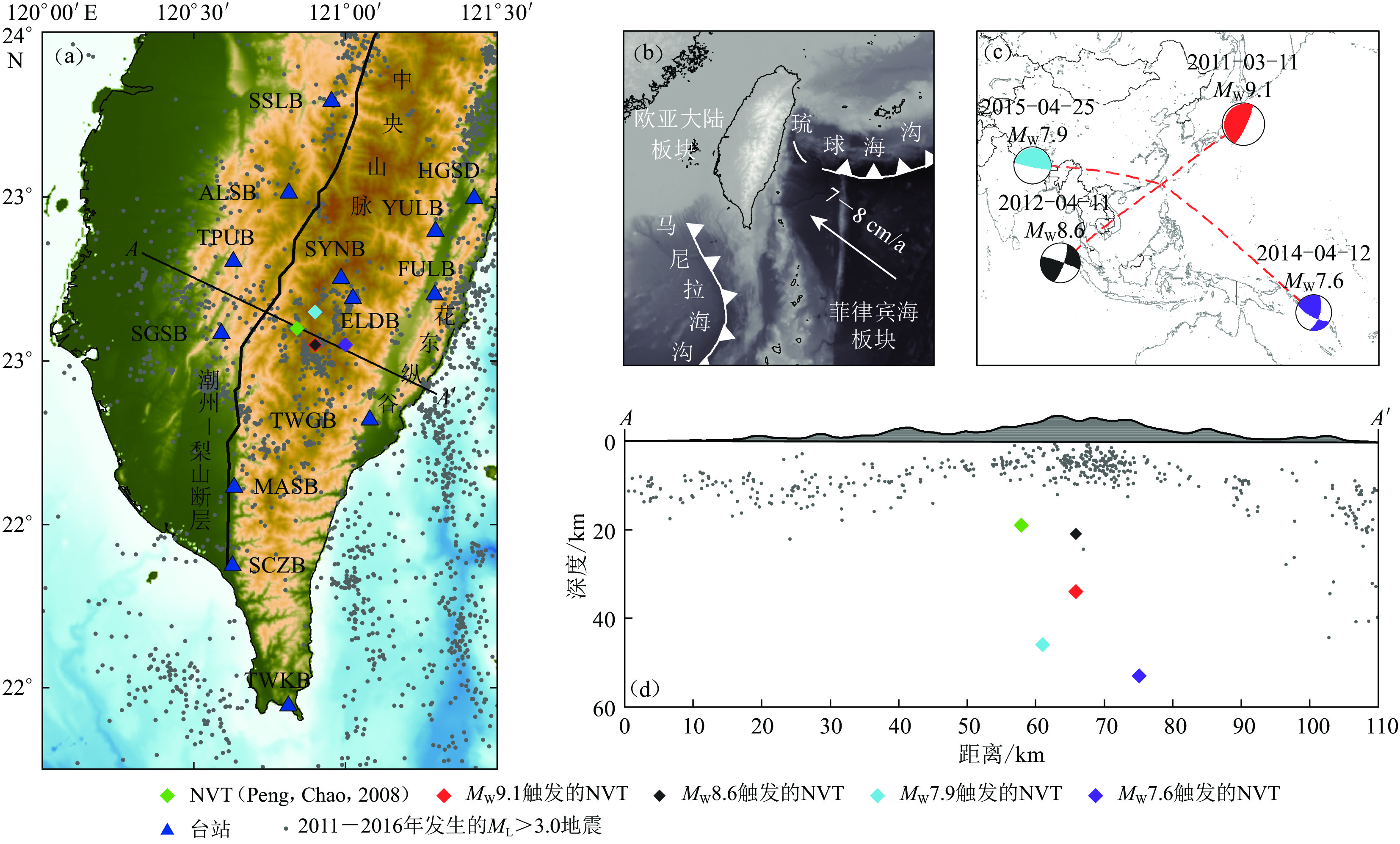
图 1 研究区域的构造背景及台站和非火山型微震颤（NVT）事件分布
（a） 研究区台站和NVT震中分布；（b） 区域构造背景；（c） 触发NVT的4次地震位置示意图；（d） AA′ 剖面上的NVT事件的震源深度分布
Figure 1. Tectonic settings and distribution of stations and non-volcanic tremor （NVT） locations
（a） Distribution of seismic stations and locations of NVTs；（b） Regional tectonic settings；（c） Schematic diagram for location of four earthquakes that triggered NVT；（d） Distribution of NVT depths along the cross-section AA′
![]()
图 2 2011年东日本MW9.1地震波形频谱分析图
（a） TPUB台站记录到的地震原始波形；（b） 2—8 Hz滤波后波形；（c） 频谱图
Figure 2. The spectrogram of Tohoku earthquake on 11 March 2011
（a） Broad-band seismogram recorded at station TPUB；（b） 2−8 Hz bandpass-filtered seismogram； （c） The spectrogram of seismogram at station TPUB
![]()
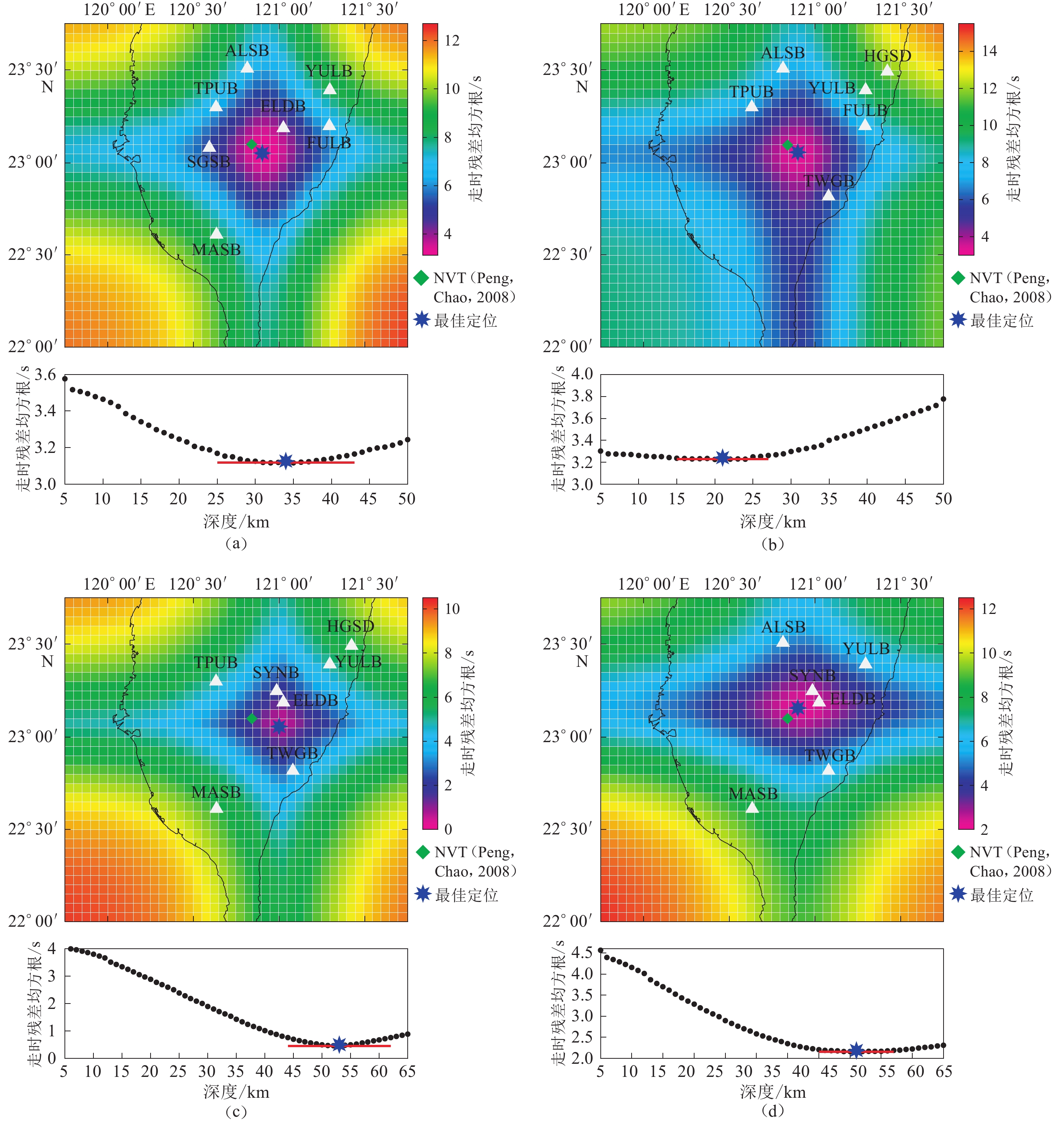
图 3 4次NVT事件的定位示意图
（a） 东日本MW9.1地震触发事件；（b） 苏门答腊MW8.6地震触发事件；（c） 所罗门群岛MW7.6地震触发事件；（d） 尼泊尔MW7.9地震触发事件
Figure 3. The schematic diagrams of locating four NVT events
（a） NVT triggered by MW9.1 Tohoku earthquake；（b） NVT triggered by MW8.6 Sumatra earthauake； （c） NVT triggered by MW7.6 Solomon earthquake；（d） NVT triggered by MW7.9 Nepal earthquake
![]()
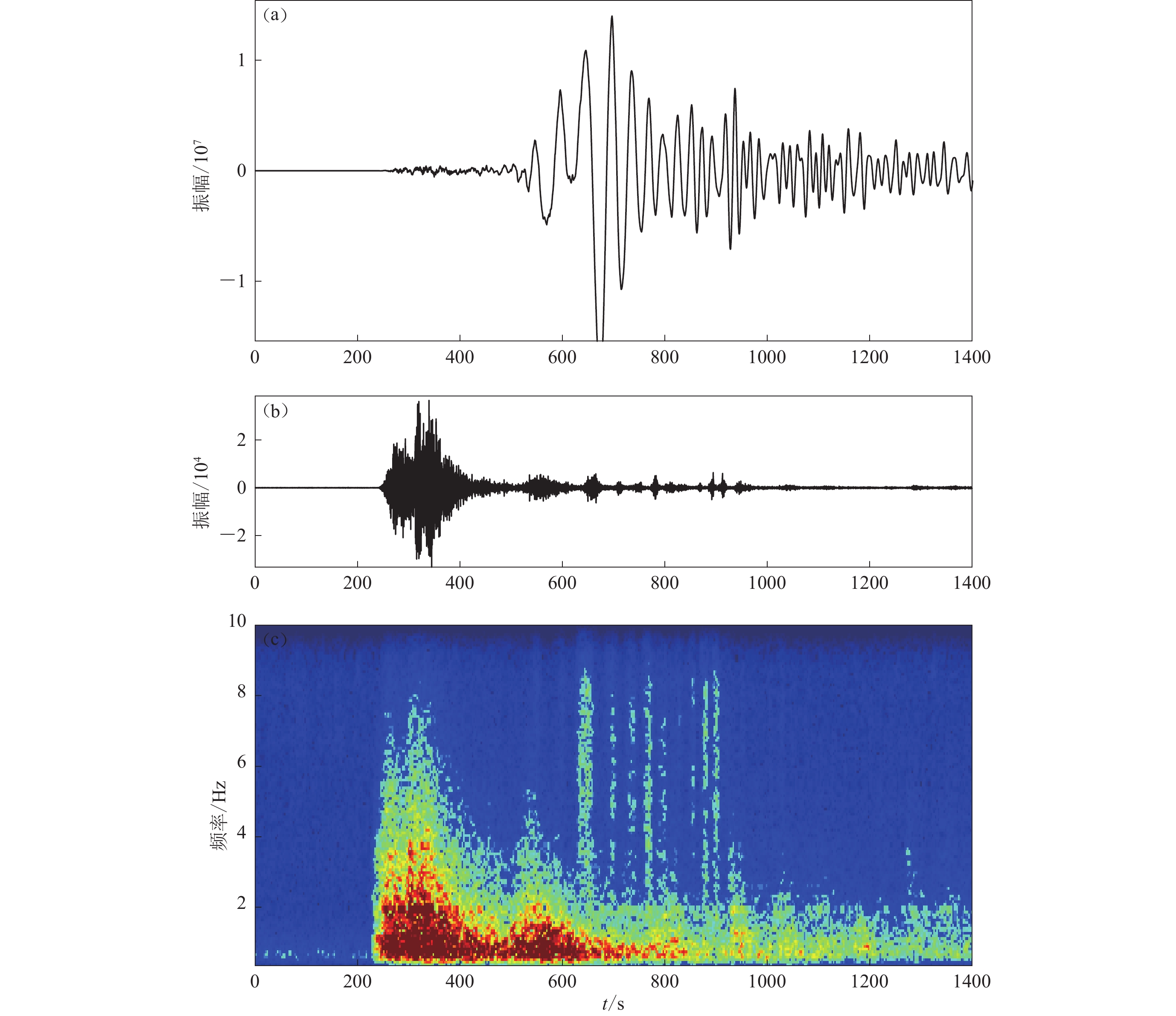
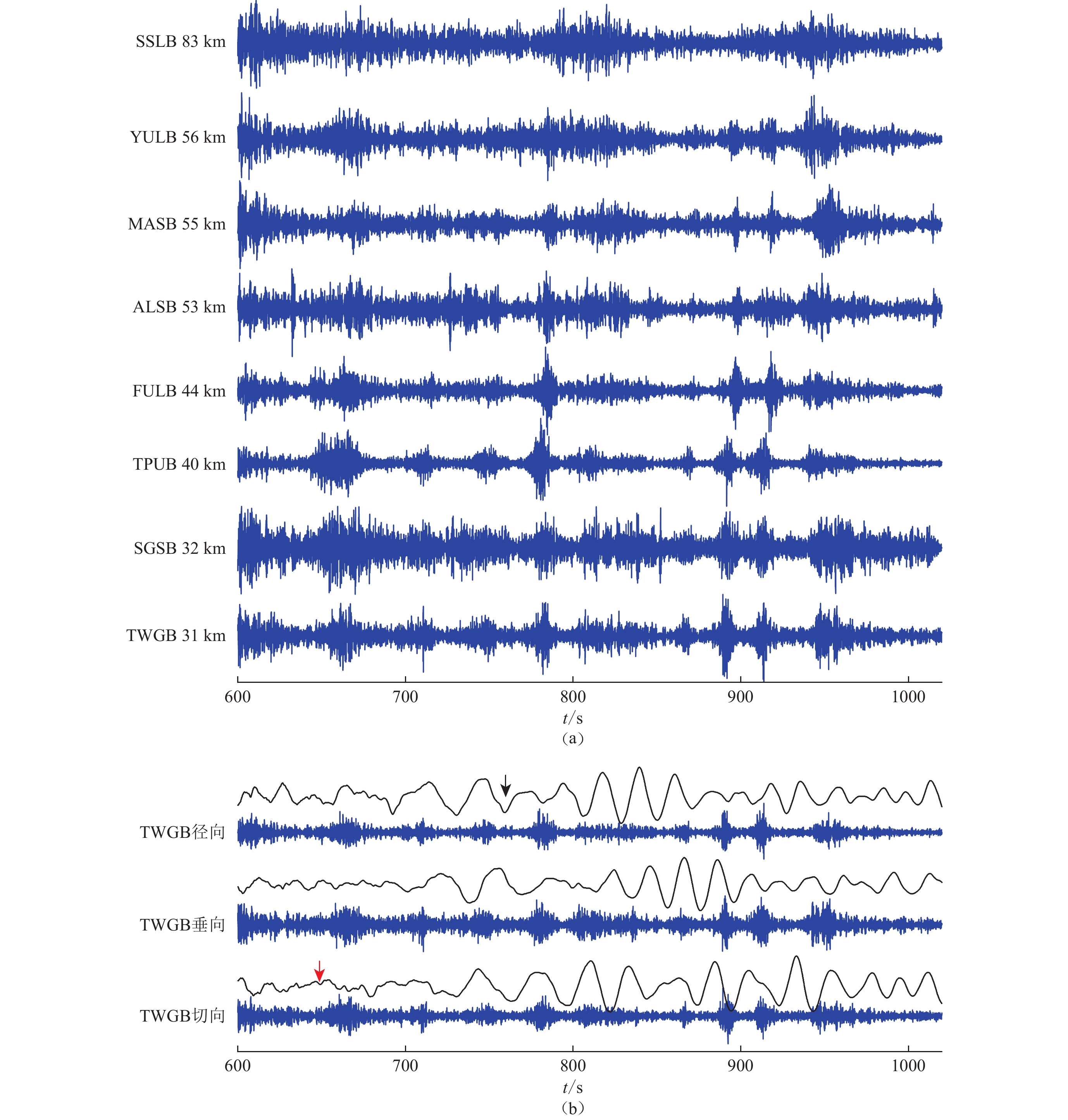
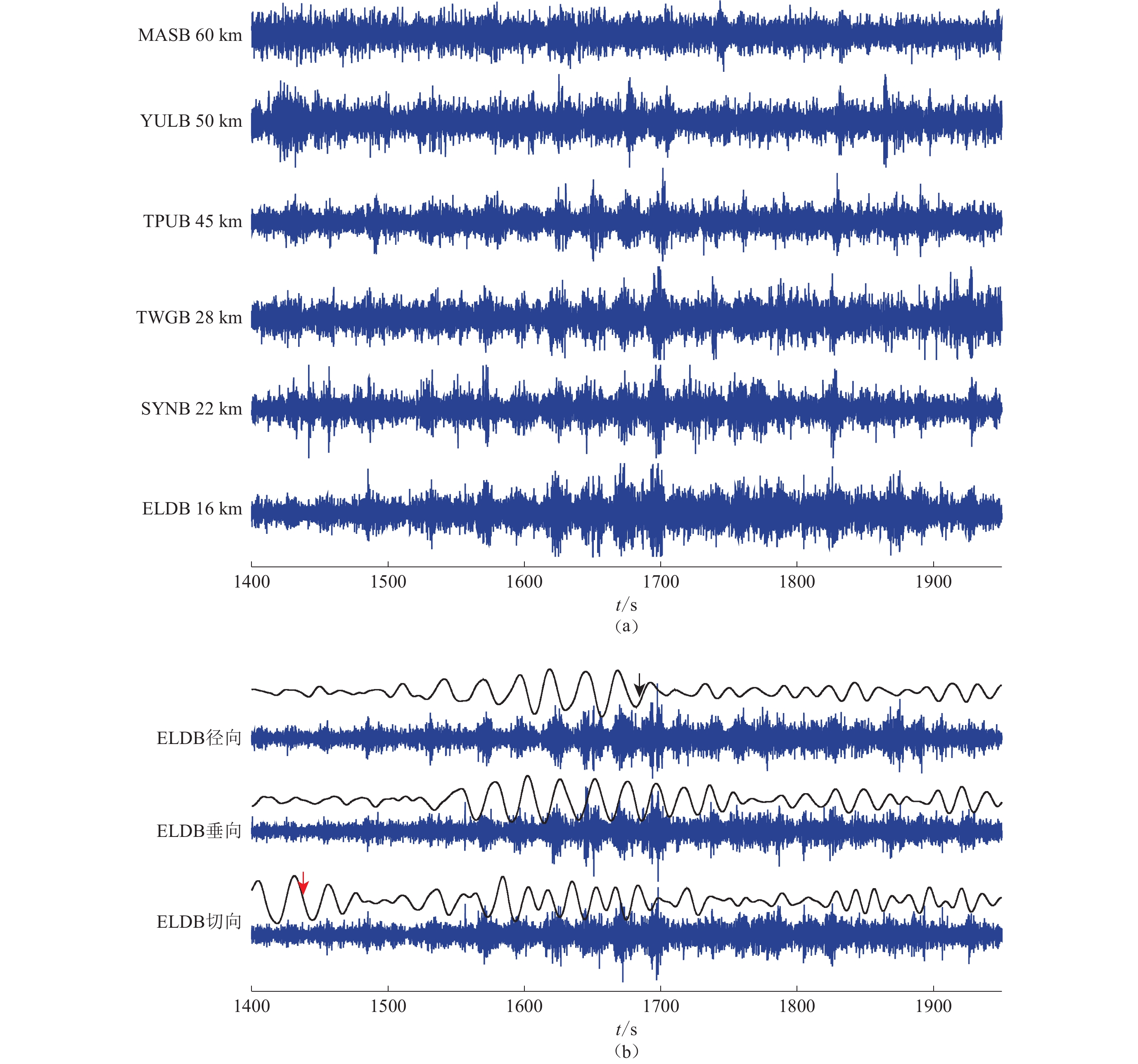
图 4 2011年3月11日东日本大地震触发的NVT事件波形图
（a） 各台站南北向分量2—8 Hz带通滤波后的波形图，波形左侧为台站名及其距NVT震源距离；（b） 仪器校正后距离NVT震源最近台站的径向、垂向、切向的波形及滤波后波形，红色、黑色箭头分别指勒夫波（4.1 km/s）和瑞雷波（3.5 km/s）理论到时，下同
Figure 4. Tremor triggered by the Tohoku earthquake on 11 March 2011
（a） The 2−8 Hz bandpass-filtered seismograms of N-S component， The hypocentral distance between each station and tremor source is shown next to the station name on left of each trace；（b） The radial，vertical and transverse component seismograms，in which instrument response has been removed，recorded at the nearest station and bandpass-filtered seismograms The red and black vertical arrows indicate the predicted arrivals of the Love and Rayleigh waves with the apparent velocity of 4.1 and 3.5 km/s，respectively，the same below
![]()
图 5 2012年4月11日苏门答腊岛地震触发NVT事件波形图
（a） 各台站南北向分量2—8 Hz带通滤波后的波形图；（b） 仪器校正后距离NVT震源最近台站的径向、垂向、切向的波形及滤波后波形
Figure 5. Tremor triggered by the Sumatra earthquake occurred on 11 April 2012
（a） The 2−8 Hz bandpass-filtered seismograms of N-S component；（b） The radial，vertical and transverse component seismograms，in which instrument response has been removed，recorded at the nearest station and bandpass-filtered seismograms
![]()
图 6 2014年4月12日所罗门群岛地震触发的NVT事件波形图
（a） 各台站南北向分量2—8 Hz带通滤波后的波形图；（b） 仪器校正后距离NVT震源最近台站的径向、垂向、切向的波形及滤波后波形
Figure 6. Tremor triggered by the Solomon earthquake on 12 April 2014
（a） The 2−8 Hz bandpass-filtered seismograms of N-S component；（b） The radial，vertical and transverse component seismograms，in which instrument response has been removed，recorded at the nearest station and bandpass-filtered seismograms
![]()
图 7 2015年4月25日尼泊尔地震触发的NVT事件波形图
（a） 各台站南北向分量2—8 Hz带通滤波后的波形图；（b） 仪器校正后距离NVT震源最近台站的径向、垂向、切向的波形及滤波后波形
Figure 7. Tremor triggered by the Nepal earthquake on 25 April 2015
（a） The 2−8 Hz bandpass-filtered seismograms of N-S component；（b） The radial，vertical and transverse component seismograms，in which instrument response has been removed，recorded at the nearest station and bandpass-filtered seismograms
![]()
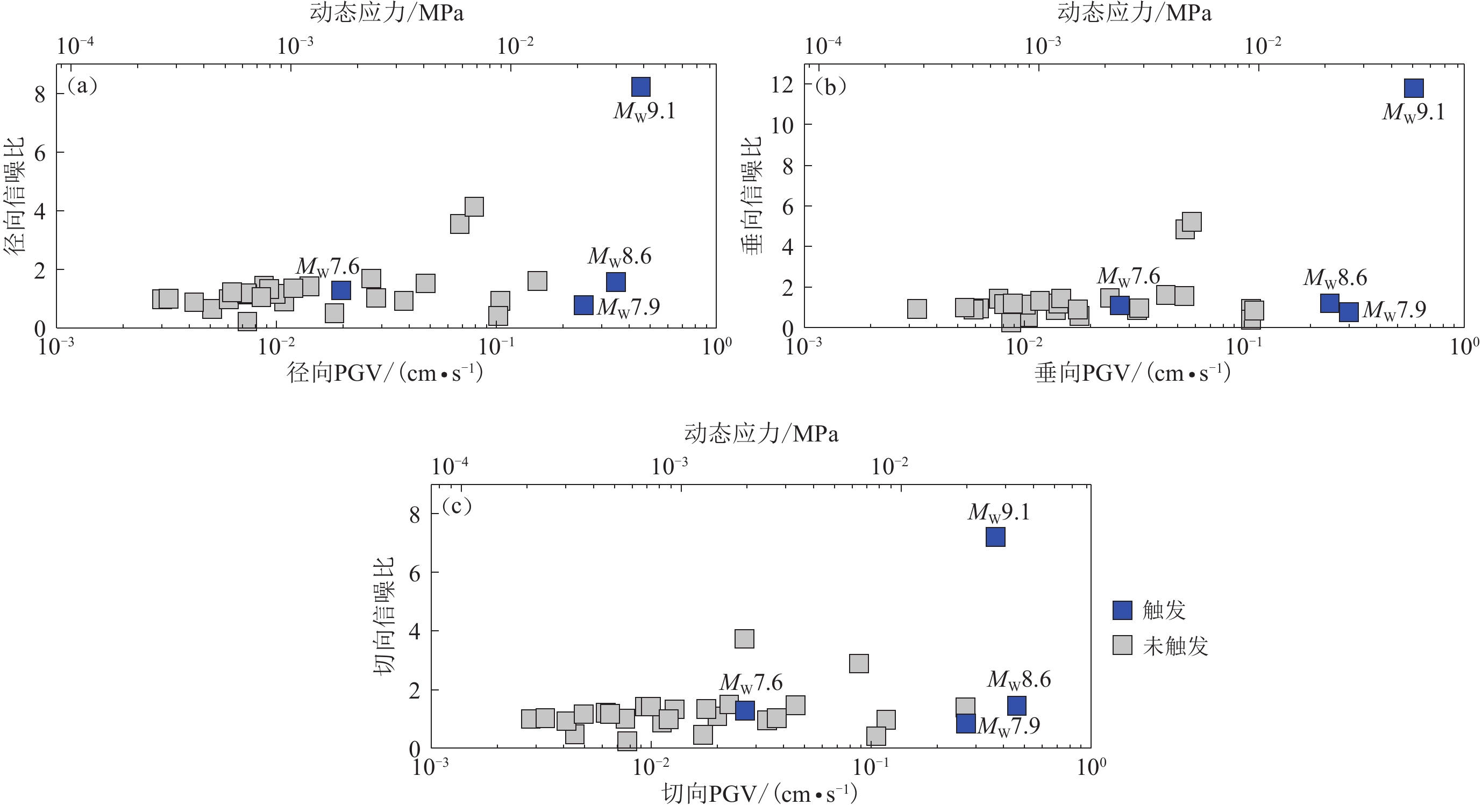
图 8 TPUB台站记录到的大地震径向 （a）、垂向 （b） 和切向 （c） 分量的PGV、动态应力及信噪比分布图
背景噪声分析时窗长度为远震事件发震前600 s
Figure 8. The scattergram of PGV，dynamic stress and signal-to-noise ratio for the radial （a），vertical （b） and tangential （c） components of the earthquakes recorded by the station TPUB
The ambient noise level of each event is calculated from a 600 s time window before the occurrence of each main shock
表 1 台湾地区一维速度模型（Wu et al，2007）
Table 1 1-D velocity model in Taiwan region （Wu et al，2007）
vP/（km·s−1） vP/vS vS/km·s−1 深度范围/km vP/（km·s−1） vP/vS vS/km·s−1 深度范围/km 3.82 1.74 2.20 0—2 6.13 1.75 3.50 21—25 4.93 1.68 2.93 2—4 6.25 1.71 3.65 25—30 5.51 1.70 3.24 4—6 6.54 1.73 3.78 30—35 5.63 1.70 3.31 6—9 7.03 1.75 4.02 35—50 5.83 1.76 3.31 9—13 8.00 1.74 4.60 50—70 5.99 1.75 3.42 13—17 8.34 1.73 4.82 70—80 6.06 1.75 3.46 17—21 
下载: 导出CSV
表 2 触发NVT的四次远震事件信息概要
Table 2 General information of the four NVT-triggered teleseismic events
发震时间 地点 震中位置 震源深度/km MW 震中距/° TPUB台站
反方位角/°年−月−日 时：分：秒 北纬/° 东经/° 2011−03−11 5：47：32.8 日本本州岛东岸近海 37.52 143.05 20.0 9.1 23.893 48 2012−04−11 8：39：31.4 苏门答腊岛北部西岸远海 2.35 92.82 45.6 8.6 34.049 236 2014−04−12 20：14：49.9 所罗门群岛 11.35 162.24 27.3 7.6 53.327 126 2015−04−25 6：11：58.6 尼泊尔 27.91 85.33 12.0 7.9 32.092 286 注：表中震中距是以TPUB台站为标准计算得到的。
下载: 导出CSV
-
陈光荣. 1993. 台湾地区QP值之空间分布及其特性[D]. 台北: 台湾大学海洋研究所: 59−60, 76−89. Chen G R. 1993. Distribution of QP in Taiwan Area and Its Characteristics[D]. Taipei: Institute of Oceanography, Taiwan University: 59−60, 76−89 （in Chinese）.
Chai B H. 1972. Structure and tectonic evolution of Taiwan[J]. Am J Sci,272(5):389–422. doi: 10.2475/ajs.272.5.389
Chao K,Peng Z G,Wu C Q,Tang C C,Lin C H. 2012. Remote triggering of non-volcanic tremor around Taiwan[J]. Geophys J Int,188(1):301–324. doi: 10.1111/j.1365-246X.2011.05261.x
Chao K,Peng Z G,Gonzalez-Huizar H,Aiken C,Enescu B,Kao H,Velasco A A,Obara K,Matsuzawa T. 2013. A global search for triggered tremor following the 2011 MW9.0 Tohoku earthquake[J]. Bull Seismol Soc Am,103(2B):1551–1571. doi: 10.1785/0120120171
Chao K,Obara K. 2016. Triggered tectonic tremor in various types of fault systems of Japan following the 2012 MW8.6 Sumatra earthquake[J]. J Geophys Res,121(1):170–187. doi: 10.1002/2015JB012566
Chen C C,Chen C S. 1998. Preliminary result of magnetotelluric soundings in the fold-thrust belt of Taiwan and possible detection of dehydration[J]. Tectonophysics,292(1/2):101–117.
Daub E G,Shelly D R,Guyer R A,Johnson P A. 2011. Brittle and ductile friction and the physics of tectonic tremor[J]. Geophys Res Lett,38(10):L10301. doi: 10.1029/2011GL046866
Fry B,Chao K,Bannister S,Peng Z,Wallace L. 2011. Deep tremor in New Zealand triggered by the 2010 MW8.8 Chile earthquake[J]. Geophys Res Lett,38(15):L15306. doi: 10.1029/2011GL048319
Gonzalez-Huizar H,Velasco A A,Peng Z G,Castro R R. 2012. Remote triggered seismicity caused by the 2011,MS9.0 Tohoku,Japan earthquake[J]. Geophys Res Lett,39(10):L10302. doi: 10.1029/2012GL051015
Han L B,Peng Z G,Johnson C W,Pollitz F F,Li L,Wang B S,Wu J,Li Q,Wei H M. 2017. Shallow microearthquakes near Chongqing,China triggered by the Rayleigh waves of the 2015 M7.8 Gorkha,Nepal earthquake[J]. Earth Planet Sci Lett,479:231–240. doi: 10.1016/j.jpgl.2017.09.024
Hill D P,Peng Z G,Shelly D R,Aiken C. 2013. S-wave triggering of tremor beneath the Parkfield,California,section of the San Andreas fault by the 2011 Tohoku,Japan,earthquake:Observations and theory[J]. Bull Seismol Soc Am,103(2B):1541–1550. doi: 10.1785/0120120114
Hsu Y J,Rivera L,Wu Y M,Chang C H,Kanamori H. 2010. Spatial heterogeneity of tectonic stress and friction in the crust:New evidence from earthquake focal mechanisms in Taiwan[J]. Geophys J Int,182(1):329–342.
Ide S. 2012. Variety and spatial heterogeneity of tectonic tremor worldwide[J]. J Geophys Res,117:B03302. doi: 10.1029/2011JB008840
Kao H,Jian P R. 2001. Seismogenic patterns in the Taiwan region:Insights from source parameter inversion of BATS data[J]. Tectonophysics,333(1/2):179–198.
Kim M J,Schwartz S Y,Bannister S C. 2011. Non-volcanic tremor associated with the March 2010 Gisborne slow slip event at the Hikurangi subduction margin,New Zealand[J]. Geophys Res Lett,38(4):L14301. doi: 10.1029/2011GL048400
Lee C P,Hirata N,Huang B S,Huang W G,Tsai Y B. 2010. Evidence of a highly attenuative aseismic zone in the active collision orogen of Taiwan[J]. Tectonophysics,489(1/2):128–138.
Miyazawa M,Brodsky E E. 2008. Deep low-frequency tremor that correlates with passing surface waves[J]. J Geophys Res,113:B01307. doi: 10.1029/2006JB004890
Miyazawa M. 2011. Propagation of an earthquake triggering front from the 2011 Tohoku-Oki earthquake[J]. Geophys Res Lett,38(23):L23307. doi: 10.1029/2011GL049795
Nadeau R M,Dolenc D. 2005. Nonvolcanic tremors deep beneath the San Andreas fault[J]. Science,307(5708):389. doi: 10.1126/science.1107142
Obara K. 2002. Nonvolcanic deep tremor associated with subduction in southwest Japan[J]. Science,296(5573):1679–1681. doi: 10.1126/science.1070378
Peng Z G,Chao K. 2008. Non-volcanic tremor beneath the Central Range in Taiwan triggered by the 2011 MW7.8 Kunlun earthquake[J]. Geophys J Int,175(2):825–829. doi: 10.1111/j.1365-246X.2008.03886.x
Peng Z G,Gomberg J. 2010. An integrated perspective of the continuum between earthquakes and slow-slip phenomena[J]. Nat Geosci,3:599–607. doi: 10.1038/ngeo940
Peng Z G,Gonzalez-Huizar H,Chao K,Aiken C,Moreno B,Armstrong G. 2013. Tectonic tremor beneath Cuba triggered by the MW8.8 Maule and MW9.0 Tohoku-Oki earthquakes[J]. Bull Seismol Soc Am,103(1):595–600. doi: 10.1785/0120120253
Peterson C L,Christensen D H. 2009. Possible relationship between nonvolcanic tremor and the 1998−2001 slow slip event,south central Alaska[J]. J Geophys Res,114(B6):B06302. doi: 10.1029/2008JB006096
Rogers G,Dragert H. 2003. Episodic tremor and slip on the Cascadia subduction zone:The chatter of silent slip[J]. Science,300(5627):1942–1943. doi: 10.1126/science.1084783
Shelly D R. 2010. Migrating tremors illuminate complex deformation beneath the seismogenic San Andreas fault[J]. Nature,463(7281):648–652. doi: 10.1038/nature08755
Tang C C,Peng Z G,Chao K,Chen C H,Lin C H. 2010. Detecting low-frequency earthquakes within non-volcanic tremor in southern Taiwan triggered by the 2005 MW8.6 Nias earthquake[J]. Geophys Res Lett,37(16):L16307. doi: 10.1029/2010GL043918
Teng L S. 1996. Extensional collapse of the northern Taiwan mountain belt[J]. Geology,24(10):949–952. doi: 10.1130/0091-7613(1996)024<0949:ECOTNT>2.3.CO;2
Wu Y M,Chang C H,Zhao L,Shyu J B H,Chen Y G,Sieh K,Avouac J P. 2007. Seismic tomography of Taiwan:Improved constraints from a dense network of strong motion stations[J]. J Geophys Res,112(B8):B08312. doi: 10.1029/2007JB004983
Yu S B,Chen H Y,Kuo L C. 1997. Velocity field of GPS stations in the Taiwan area[J]. Tectonophysics,274(1/2/3):41–59.
-
期刊类型引用(3)
1. 刘建锋，赵呈星，代航宇，魏进兵，杨建雄. 流体注入诱发页岩断层失稳活化试验研究. 采矿与岩层控制工程学报. 2025(01): 53-66 . 
百度学术
2. 苏培东，陆星好，徐学渊，邱鹏，李有贵. 油气开采过程中地质环境问题研究现状与展望. 安全与环境工程. 2024(02): 147-163+172 . 百度学术
3. 王子韬，吴忠良，张怀. 工业生产诱发地震成因与研究进展. 地球与行星物理论评(中英文). 2024(04): 428-439 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1133
- HTML全文浏览量: 750
- PDF下载量: 38
- 被引次数: 5
