Earthquake and explosion identification based on Deep Learning residual network model
-
摘要: 为加强对地震台网记录的天然地震与人工爆破事件进行准确的性质识别,本文基于深度学习技术中的残差网络模型,提出了一种新的爆破识别方法,并根据北京数字遥测地震台网及国家数字测震台网中心记录的波形数据及其发布的包含事件性质的地震报告,选取河北三河采石场的93次爆破事件和54次周边地震事件的波形功率谱,分别采用不同的训练样本比例进行了100次和1 000次独立的随机抽样子试验以及 “留一交叉验证法” 试验,对人工爆破与天然地震进行了识别研究。试验结果表明,深度学习残差网络模型在天然地震与爆破事件的性质识别中具有很高的识别率且效果稳定,具有较好的应用前景。Abstract: In order to enhance the property identification of earthquakes and explosions recorded by seismic network, this paper proposed a new technology of explosion discrimination based on the residual network model in Deep Learning technology, and utilized it to identifying explosion and surrounding earthquakes in Sanhe Quarry of Hebei Province. According to the waveform data recorded by the Beijing Digital Telemetry Seismic Network and China Center of Digital Seismic Network, and the released seismic phase reports, we analyzed the waveform power spectrum of 93 explosion events and 54 surrounding seismic events in Sanhe Quarry of Hebei Province. Moreover, 100 independent random sampling sub-tests, 1 000 independent random sampling sub-tests and leave-one-out-cross-validation test were conducted by adopting different training sample proportions, respectively. The test results show that the residual network model in Deep Learning has a high recognition rate and a stable effect in identifying the property of earthquakes and explosions, therefore it has a wonderfully potential application.
-
引言
天然地震与人工爆破事件的识别研究,对于安全生产、国防安全和地球科学研究以及高质量地震数据的创建具有重要意义,准确地、自动地区分天然地震与人工爆破事件始终是相关研究中的热点问题(Stump et al,2002 ;Rabin et al,2016 )。区域地震目录中经常混杂着工人爆破事件,导致地震危险性评估不准确(Kortström et al,2016 ),因此在分析微震活动性时需要从地震目录中剔除人工爆破事件(Wiemer,2000),而人工爆破事件又会引发构造应力释放剪切分量,增加了天然地震与爆破事件的判识难度。
自20世纪50年代起,对天然地震与人工爆破事件的识别就开始了广泛深入的研究,并提出了多种识别判据,包括P波初动、震源深度、体波震级mb与面波震级MS之比、倒谱、P波与S波震相幅值比以及从频率域中提取的判据等(王婷婷等,2013)。这些单特征向量最初通常被单独使用,但当爆炸当量较小时,其识别效果并不理想(杨宏,贾维敏,2000),因此利用多个判据进行综合识别成为主要的研究方向。天然地震相较于人工爆破事件会产生更多的低频信息(Tiira,1995),因此从频率域中提取的判据常用于事件识别,而且频率域判据较时域判据具有更好的判识效果(Falsaperla et al,1996 )。随着神经网络研究的兴起,频率域信息或频率域和时域混合信息与人工神经网络相结合的方法应用于天然地震与人工爆破的识别中,有效地提高了事件的识别能力(Esposito et al,2006 ;Kuyuk et al,2011 ;AitLaasri et al,2013 ;Vallejos,McKinnon,2013;Riggelsen,Ohrnberger,2014;Reynen,Audet,2017)。
由于早期人工神经网络受限于算法和当时硬件的计算能力,在面对海量的地震数据时,未能将事件的全部频谱信息输入网络,仅从频谱信息中预先提取某些特征(如P/S型谱比值)对数据进行降维使用,不但增加了处理过程的复杂性,而且损失了大量的事件信息,模型极易陷入局部最优解。在网络层数很深的情况下,神经网络参数众多,使得模型训练速度非常缓慢,容易出现梯度消失现象,进而导致模型的泛化能力不强。
近年来,深度学习技术在大量智能计算任务中得以广泛应用,在很多方面带来了超出预期的效果,例如语音处理(Lee et al,2009 ;Dahl et al,2011 )、视觉计算和自然语言理解、搜索、推荐,尤其在图像分类、图像分割、目标检测(Ren et al,2015 )、事件检测、动作识别和场景识别等视觉信息处理方面均取得了显著的进步(山世光等,2016)。深度学习的概念源于人工神经网络研究,是人工神经网络的延伸和发展,它通过低层特征组合形成更加抽象的高层表示属性类别或特征,以寻求数据的分布式特征表示(孙志军等,2012),两者本质上都是从大量训练样本中学习统计规律,从而对未知事件作出预测,但深度学习模型在处理大样本和复杂的函数关系时更为便捷。
为提高天然地震事件与人工爆破事件的识别率,本文拟应用深度学习技术,在该领域尝试使用可以训练超深网络的残差网络模型(residual network),探索使用波形的全部功率谱作为模型训练与测试的输入数据,而非在频率域中预先提取若干个判据或者选取部分波形的频域数据进行降维使用,以期简化数据的预处理流程,在模型训练过程中保留事件更多的原始信息,进一步提高事件的识别能力。
1. 方法
1.1 深度残差网络模型基本原理
模型深度是图像识别和分类任务中非常重要的因素(Simonyan,Zisserman,2015;Szegedy et al,2015 ),模型深度越深,对于图像的抽象刻画能力越强,但同时会出现梯度消失或梯度爆炸现象(Bengio et al,2002 ),从而影响模型的收敛,不容易找到全局最优解。为解决该问题,He等(2016)提出了深度残差网络模型。理论上,只要硬件能力允许,该模型可以训练多达上千层深的网络。受限于计算机运算能力,本文仅采用14层网络。该模型的基本结构如图1所示。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {{y}} {\text{=}} {\cal{F}}\left({{x}} \right) {\text{+}} {{x}}{\text{,}} $


(1) 其目的是使输入数据的信息随着卷积层数的增加而不会减弱,有利于随后的映射层拟合输入数据。式(1)中,
$ {\cal{F}}\left({{x}} \right) {\text{=}} {{{W}}_{\bf{2}}}\delta \left({{{{W}}_{\bf{1}}} \cdot {{x}}} \right){\text{,}} $


(2) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$ {{y}} {\text{=}} {\cal{F}}\left({{{x}},\left\{ {{{{W}}_{{i}}}} \right\}} \right) {\text{+}} {{{W}}_{{S}}} \cdot {{x}}{\text{.}} $


(3) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
1.2 模型的构建
实际应用中,残差网络模型的结构多样,其中卷积层中的卷积核大小、池化层大小、输入数据形状、通道数量以及快捷链接跨越层数等均根据经验设置,并非固定不变,细微的差别并不会影响模型的收敛效果。
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
![]() 图 2 本文应用的残差网络模型图中省略了4层卷积核为64和128的卷积层,加上全连接层及分类器层,共计14层,图中上方数字2×2为卷积核大小,下方数字为卷积核的数量Figure 2. The residual network model applied in this paperThe four convolutional layers with 64 and 128 convolution kernels was omitted;coupled with the fully connected layer and the classifier layer,there are 14 layers in total。2×2 on the upper in the figures is the size of the convolution kernel,and on the bottom is the number of the convolution kernel表 1 各卷积层输入及输出的通道数量Table 1. The number of channels for input and output of each convolution layer
图 2 本文应用的残差网络模型图中省略了4层卷积核为64和128的卷积层,加上全连接层及分类器层,共计14层,图中上方数字2×2为卷积核大小,下方数字为卷积核的数量Figure 2. The residual network model applied in this paperThe four convolutional layers with 64 and 128 convolution kernels was omitted;coupled with the fully connected layer and the classifier layer,there are 14 layers in total。2×2 on the upper in the figures is the size of the convolution kernel,and on the bottom is the number of the convolution kernel表 1 各卷积层输入及输出的通道数量Table 1. The number of channels for input and output of each convolution layer卷积层 输入通道数 输出通道数 卷积层 输入通道数 输出通道数 卷积层 输入通道数 输出通道数 1 1 8 6 32 64 11 256 256 2 8 16 7 64 64 12 256 512 3 16 16 8 64 128 13 512 512 4 16 32 9 128 128 14 全连接 5 32 32 10 128 256 需要注意的是,在本模型中,连接快捷链接的输入数据与相应卷积层的输出数据维度不一致,不能直接相加,故将输入数据二维平面的边缘补0来保持与输出数据维度的一致性。此外,当输入数据维度较高时,卷积层与卷积层之间需设有池化层以对数据进行降维,本文的输入数据维度仅为200,故未进行池化。
2. 数据预处理
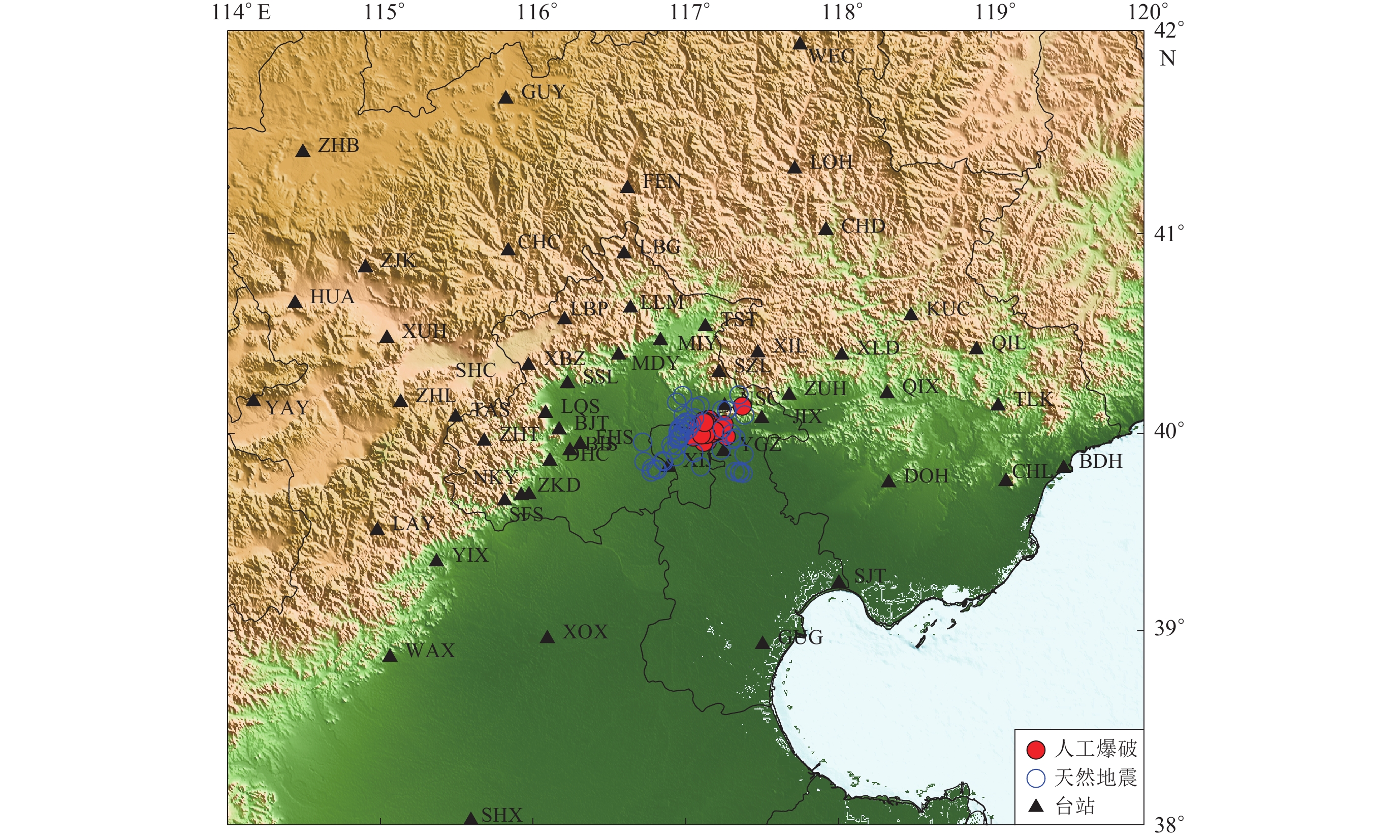
根据北京遥测数字地震台网及国家数字测震台网中心提供的波形数据和事件目录,事件性质由国家数字测震台网中心判定。试验数据选自2010—2016年期间发生在河北三河地区(39.8ºN—40.3ºN,116.8ºE—117.4ºE)有明确分类的天然地震事件54次,人工爆破事件93次,震级范围为ML1.5—3.0,震中距范围为5—260 km。研究区内分布100个观测台站,每次事件根据理论到时截取这100个台站记录到的三分向记录,后续的波形筛选在此基础上进行,事件和台站分布如图3所示。
由于本文采用的事件发生在城市边缘地区,部分台站受震中距和自身监测能力的影响,事件信息中所含各类噪声的影响较大。因此,在开展研究之前需要进行筛选,剔除被噪声淹没的台站波形,之后对剩余波形进行功率谱估计。
2.1 波形筛选
本文选用短长时窗平均比(short-term average/long-term average,缩写为STA/LTA)方法(Stevenson,1976;Baer,Kradolfer,1987;刘晗,张建中,2014)并结合能量算子(Teager-Kaiser energy operator,缩写为TKEO)对地震波形数据进行预处理,挑选出有效信号。STA/LTA的基本思想是利用信号短时窗平均值(STA)与长时窗平均值(LTA)之比来研究能量或振幅的变化,当某一点比值大于设定阈值时,视为事件发生。TKEO能够准确地追踪信号的瞬时能量变化,对微小事件有很好的识别效果。本文针对三分向波形中的垂直分量进行研究,整个筛选流程如下:
1) 对波形数据进行预处理,去除仪器响应和均值倾向;
2) 根据事件发震时刻和震中距,选取合理的速度窗口截取包含理论P波和S波在内的全波段波形;
3) 对数据进行1—25 Hz带通滤波,消除长周期噪声干扰;
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
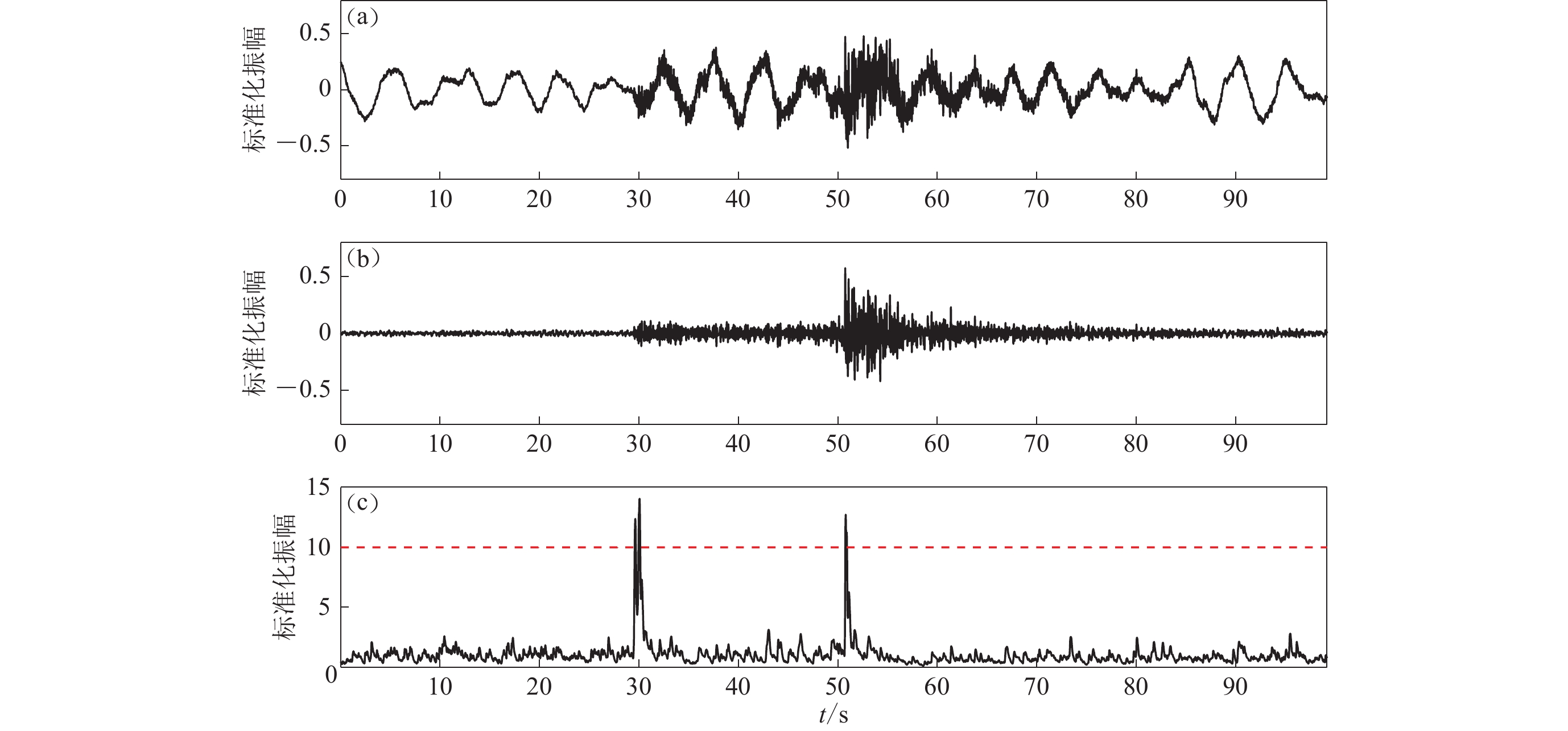
由图4可以看出,原始数据受长周期噪声影响严重(图4a),但经滤波之后(图4b)P波和S波发育清晰,信噪比较高。图4c中波起始位置的STA/LTA值高于红色虚线,与人工判定结果一致。以上示例说明,STA/LTA方法在信噪比较低的情况下依然能对训练样本进行准确的筛选,具有较强的实用性。
按照上述步骤筛选天然地震和人工爆破的有效波形,每次事件最终保留样本数据数十份不等,这样形成了3 995份波形数据,较传统人工挑选波形节约时间,效率更高。
2.2 功率谱估计
理论研究表明,由于震源性质不同,人工爆破和天然地震具有不同的主频、拐角频率和频带宽度(Bennett,Murphy,1986;Hong,2013),这些差异或多或少能够呈现在频谱上。台站接收到的天然地震和人工爆破可以看作随机信号,频率分布服从一定的统计规律。功率谱密度作为频谱分析的重要手段,在数学计算上等于振幅谱的平方,将其作为识别判据可以放大地震和爆炸的频域差异。本文采用Welch平均周期法(郝春月等,2012)对筛选出的波形数据进行谱估计。
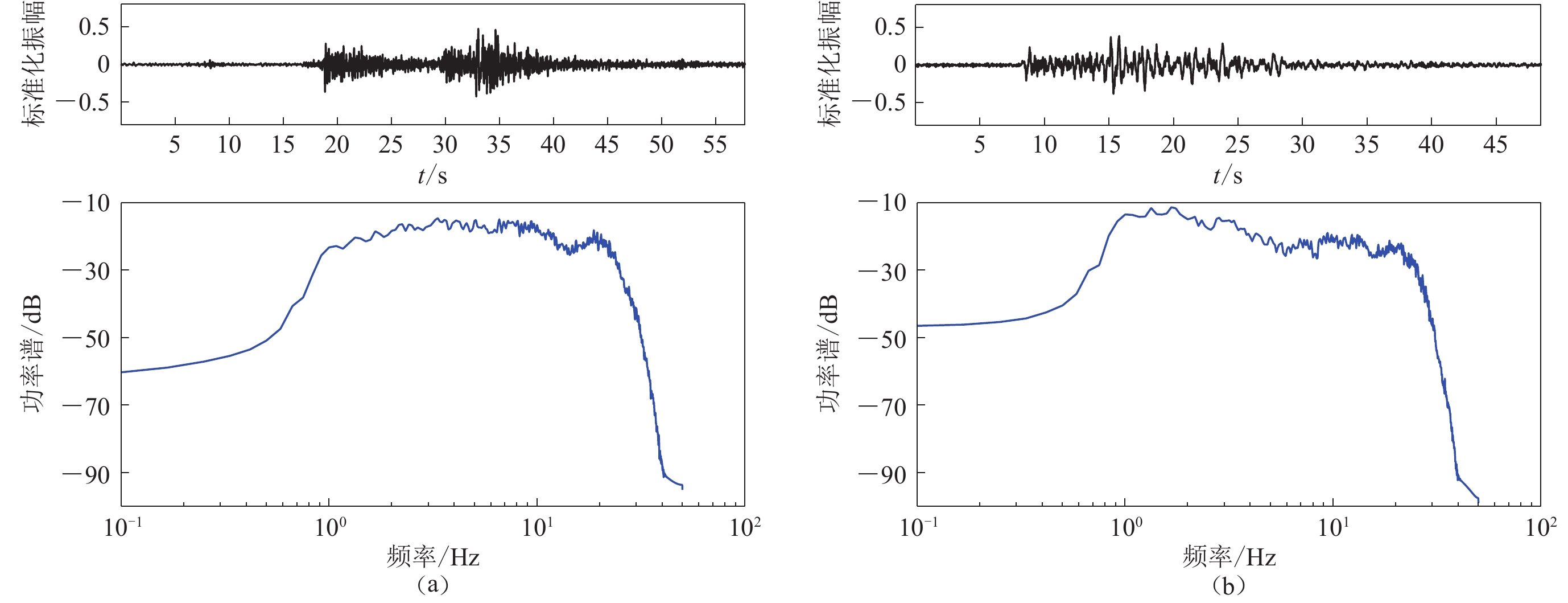
频谱分析的优势在于不受震源和震中距影响,不同台站记录的天然地震和人工爆破事件的总长度各不相同,但在频域的功率谱密度长度一致,不影响后续的训练和识别,选取2012−01−18 23:03:54.6和2010−01−22 15:40:26.6震级同为MS2.0的天然地震和人工爆破事件,震中位置分别为(39.803°N,117.352°E)和(40.049°N,117.139°E);震中距分别为Δ=67.52 km和Δ=65.07 km, 对两事件进行信号功率谱对比,结果如图5所示。
由图5可见,爆炸信号功率谱在1—5 Hz低频部分明显高于地震信号,高频区域在分布规律上与地震相似。由于单一样本不能反映整体类别的频谱特征,本文将功率谱作为训练和测试数据,对筛选出的每一条数据进行功率谱估计,为后续的训练与判别奠定基础。
3. 训练集和测试集的创建及测试过程
训练集和测试集分别用于模型的训练和测试,两个集合分别包含若干个天然地震样本和人工爆破样本,且两个集合之间的样本互不重叠。集合中每个样本均由事件波形的功率谱和标签组成。每个样本的功率谱由200个谱值构成,以其为模型的输入;将天然地震样本标签标注为0,人工爆破样本标签标注为1,之后对标签进行one-hot编码,将其作为观测值,而将模型的输出作为模型的预测值,模型训练的目的为使训练集的输出值分布与观测值的分布尽量一致,即输出值的分布与预测值的分布之间的差值尽可能小,其差值定义为损失函数,本文采用的损失函数为交叉熵,优化函数采用自适应矩估计(adaptive moment estimation,缩写为Adam)(Kingma,Ba,2015)。自适应矩估计是一种计算每个参数不同更新速率的方法,它利用梯度的一阶矩估计和二阶矩估计动态地调整每个参数的学习率,其优点主要在于经过偏置校正后,每一次迭代学习率均有个确定范围,使得参数比较平稳。
为了验证模型的准确率和稳定性,本文进行两组随机抽样试验和一组留一交叉验证试验。前两组随机抽样试验中,每组试验各进行100次和1 000次独立的随机抽样子试验。第一组试验中,每次子试验从天然地震和人工爆破中各随机抽取20次事件构成训练集进行训练,余下的样本作为测试集。第二组试验中,每次子试验从天然地震和人工爆破中分别随机抽取27次和46次事件构成训练集进行训练,余下的样本作为测试集。第三组试验中,采用留一交叉验证法(Kohavi,1995)进行试验,即每次子试验从147次事件中留下一个事件作为测试,其它146次事件全部用于模型训练,该步骤将一直持续到每次事件都被作为一次测试事件时结束,这样最终可得到147次测试结果,其平均值用于计算模型的准确率,因此需要进行147次子试验。
在前两组100次和1 000次随机抽样的子试验中,将每次输入模型的样本数量即块尺寸(batch_size)设置为训练集的全部样本,由于未采用分批输入的方式,所以每次子试验只进行100次或1 000次父循环(训练)。而在第三次试验中,块尺寸设置为500个样本,因每次输入模型的样本数量并非训练集的全部样本数,一次父循环(训练)过程中会将全部样本分为若干批次输入模型进行子循环(训练),所以每次子试验的父循环(训练)次数可相应减少,本文选取3次父循环(训练)。子循环(训练)次数即批次为:训练样本数/块尺寸-1。需要指出的是,父循环(训练)次数和块尺寸大小,可根据GPU的内存大小以及模型收敛的速度进行调整。一般来说,块尺寸越大,批次越小,子循环(训练)次数就越少,因此需要更多的父循环(训练)才能使模型收敛。另外GPU内存的大小,也决定块尺寸并不能设置为无限大。
在计算速度方面,模型训练时间受样本量大小、模型复杂程度、迭代次数以及计算机运算能力的影响而长短不一。以本文为例,单次训练过程(1 000次迭代)的时间在2分钟左右。而测试过程是在模型参数都训练完毕后进行,只是输入和输出的过程,所以计算相当迅速,仅需毫秒即可完成。
4. 研究结果
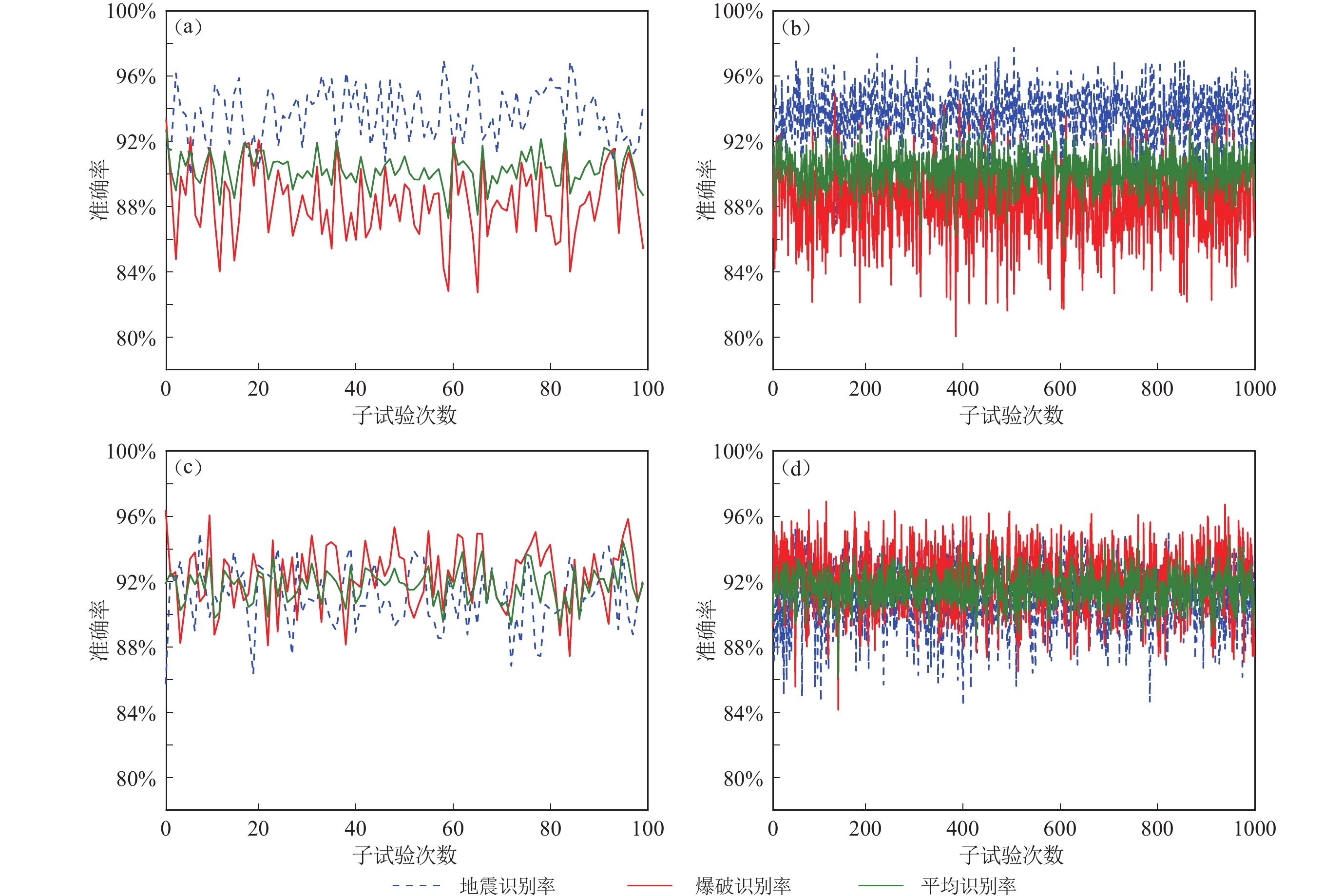
若以每个测试样本(台站记录)是否被正确识别作为评判标准(基于记录),则第一组试验的100次子试验的平均识别率、地震平均识别率和爆破平均识别率分别为90.3%,93.6%和88.3%;1 000次子试验的平均识别率、地震平均识别率和爆破平均识别率分别为90.2%,93.6%和88.3%。第二组试验的100次子试验的平均识别率、地震平均识别率和爆破平均识别率分别为91.7%,91.0%和92.3%;1 000次子试验的平均识别率、地震平均识别率和爆破平均识别率分别为91.6%,90.6%和92.1%。详细结果见图6。
![]() 图 6 基于台站记录的试验结果图(a)和(b)为第一组试验中的100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(c)和(d)分别表示第二组试验中100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取 27和46次事件进行训练,余下的事件作为预测Figure 6. Test results based on station recordsFigs. (a) and (b) are the results for the 100 random subtests and 1 000 random subtests in the first group, each subtest selects 20 events from earthquakes and explosions for training,and the remaining events are used as predictions;Figs. (c) and (d) are the results for 100 random subtests and 1 000 random subtests in the second group,each subtest selects 27 and 46 events from earthquakes and explosions for training,and the remaining events are used as predictions
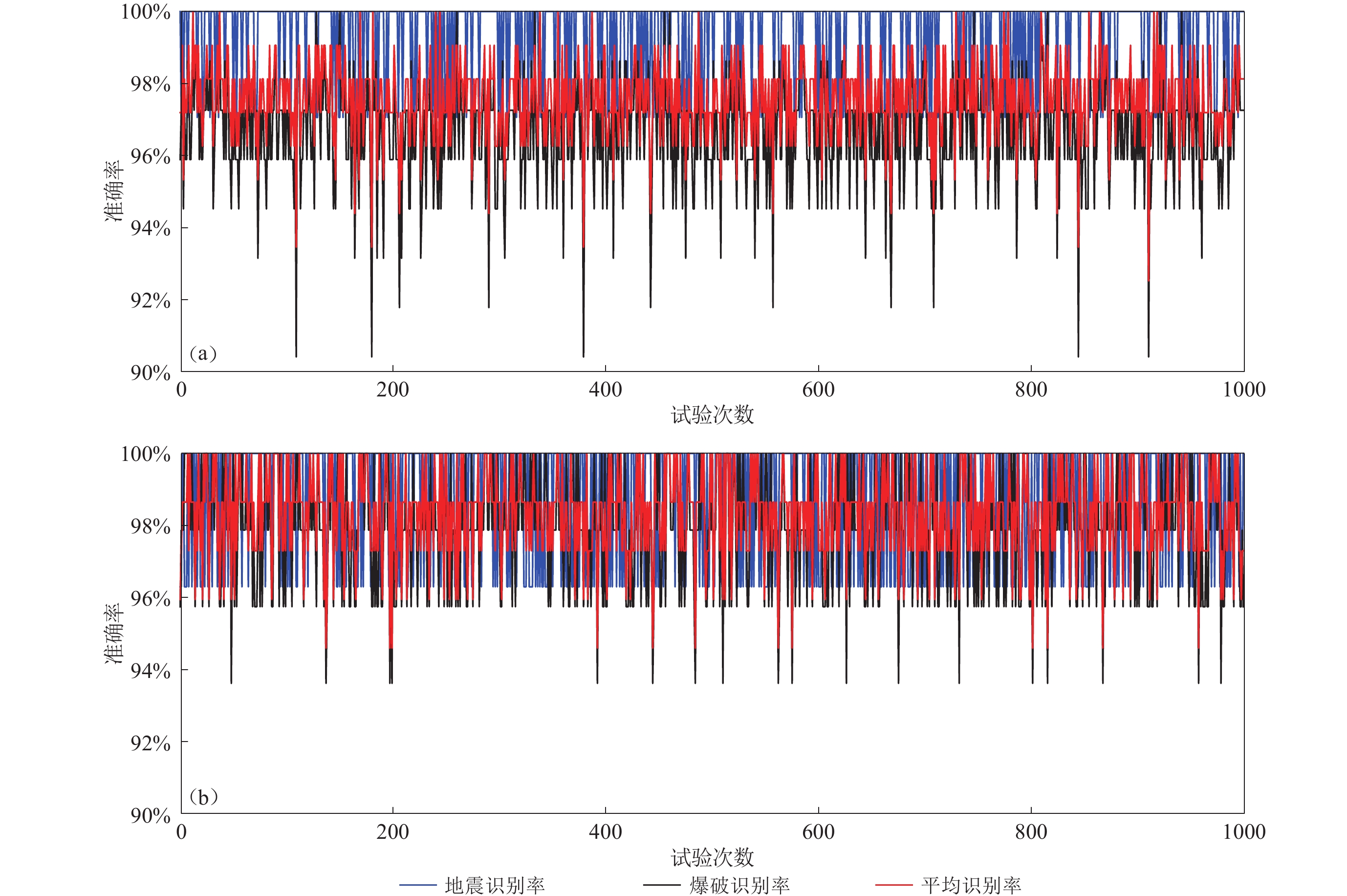
图 6 基于台站记录的试验结果图(a)和(b)为第一组试验中的100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(c)和(d)分别表示第二组试验中100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取 27和46次事件进行训练,余下的事件作为预测Figure 6. Test results based on station recordsFigs. (a) and (b) are the results for the 100 random subtests and 1 000 random subtests in the first group, each subtest selects 20 events from earthquakes and explosions for training,and the remaining events are used as predictions;Figs. (c) and (d) are the results for 100 random subtests and 1 000 random subtests in the second group,each subtest selects 27 and 46 events from earthquakes and explosions for training,and the remaining events are used as predictions若以每次事件基于50%,60%和70%的台站记录被正确识别作为评判标准(基于事件)统计,准确率会进一步提高。为保持图表简洁,仅将基于50%的台站记录被正确识别作为评判标准(基于事件)的结果列于表2。同时,给出基于 50%和60% 台站记录被正确判别为识别标准(基于事件)的100 次随机子试验进程及结果(图7),同时给出基于 50%台站记录被正确判别为识别标准(基于事件)的1 000 次随机子试验进程及结果(图8)。此外,采用留一交叉验证对模型的准确率和稳定性进行验证,因留一交叉验证试验中每次测试(子试验)仅有一次事件,基于事件的识别率仅当全部子试验完毕后才能给出,因此仅存在最终识别率,不存在平均识别率、最高识别率和最低识别率。结果显示:若以每次事件超过50%,60%和70%的台站记录被正确识别作为评判标准(基于事件),最终识别率分别为97.3%,95.2%和93.9%。为进行方法对比,基于50%台站记录被正确识别作为评判标准(基于事件)的结果列于表2。
表 2 基于事件的3组试验结果对比Table 2. Comparison of the three groups of event-based test results试验组 随机子
试验次数基于50%记录被正确
判别的平均识别率基于50%记录被正确
判别的地震识别率基于50%记录被正确
判别的爆破识别率平均值 最大值 最小值 平均值 最大值 最小值 平均值 最大值 最小值 第一组 100 97.7% 100% 93.5% 99.4% 100% 97.1% 96.9% 100% 91.8% 1 000 97.6% 100% 92.5% 99.3% 100% 97.1% 96.8% 100% 90.4% 第二组 100 98.4% 100% 95.9% 98.7% 100% 96.3% 98.3% 100% 93.6% 1 000 98.3% 100% 94.6% 98.8% 100% 90.5% 98.1% 100% 93.6% 留一交叉验证 97.3% 96.3% 97.8% ![]() 图 7 基于事件的100次随机子试验结果图(a)为第一组试验中的100次随机子试验,每次的子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(b)为第二组试验中的100次随机子试验,每次子试验从地震和爆破中分别抽取27和46次事件进行训练,余下的事件作为预测。图中红、蓝线条分别代表基于50%,60%台站记录被正确判别为识别标准(基于事件)的识别率Figure 7. Results of 100 random subtests based on the eventsFigs. (a) and (b) represent 100 random subtests in the first group and the second group,respectively. Fig. (a) indicates that each subtest takes 20 events from the blasting and earthquakes for training,and the remaining events are used as predictions;Fig. (b) indicates that each subtest takes 46 and 27 events from the blasting and earthquakes for training,and the remaining events are used as predictions.
图 7 基于事件的100次随机子试验结果图(a)为第一组试验中的100次随机子试验,每次的子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(b)为第二组试验中的100次随机子试验,每次子试验从地震和爆破中分别抽取27和46次事件进行训练,余下的事件作为预测。图中红、蓝线条分别代表基于50%,60%台站记录被正确判别为识别标准(基于事件)的识别率Figure 7. Results of 100 random subtests based on the eventsFigs. (a) and (b) represent 100 random subtests in the first group and the second group,respectively. Fig. (a) indicates that each subtest takes 20 events from the blasting and earthquakes for training,and the remaining events are used as predictions;Fig. (b) indicates that each subtest takes 46 and 27 events from the blasting and earthquakes for training,and the remaining events are used as predictions.5. 讨论与结论
为探索将深度学习技术在天然地震与人工爆破的识别中的应用,本文尝试在该领域应用可以训练超深网络的残差网络模型。研究中,将波形的全部功率谱作为模型训练与测试的输入数据。为了测试模型的识别率和稳定性,共进行了3组对比试验,前两组试验中分别依据训练样本比例不同各进行了100次和1 000次随机抽样子试验,第3组试验采取留一交叉验证法进行了测试。根据以上试验的结果,得到如下认识:
1) 以超过50%的台站记录被正确识别(基于事件)作为判别标准较为客观。结果显示:按照50%的判别标准,前两组试验的100次随机试验平均识别率分别为97.7%和98.4%,1 000次随机试验平均识别率分别为97.6%和98.3%;第3组试验的识别率为97.3%。
2) 3组比较接近的试验结果表明,在训练集达到总样本的一定比例后,训练集的大小对结果影响并不大,模型可从有限的样本中统计出样本的规律,展现出模型强大的学习能力和泛化能力。另外,分析认为,事件的波形功率谱除了震中距的因素,一定程度上消除了传播路径的影响,更能反映出震源的信息,为该模型较高的识别率奠定了基础。
前两组试验中,相同随机抽样数量下的1 000次与100次随机试验的平均识别率仅相差0.1%,且在1 000次随机试验(基于事件)的结果(图8)中,可以清晰地看到,平均识别率、地震识别率、爆破识别率的分布均呈现条带状,仅有少数值偏离条带,这些结果充分展示出模型对于地震和爆破的识别不受试验次数的影响,具有非常高的识别率和稳定性。
本文中的天然地震事件和人工爆破事件在空间上呈现包围分布,如图3所示,具有明显的规律性。对于这种有规律性的样本分布,模型采用较少的训练样本就可找到样本的统计规律。而对于复杂的空间分布,则需要更多的样本进行训练。
虽然本文研究的区域仅限于河北三河采石场及周边地区,模型经过训练后得到的模型参数不能完全适用到其它地区,但就模型和方法而言具有很好的通用性和稳定性。此外,可以将多个地区的天然地震和人工爆破统一进行训练和测试,这样得到的模型参数会更具有普适性。另外,本文采用的模型深度仅为14层,还可将模型深度进一步加深,预计可以进一步提高模型的识别率。
波形功率谱作为训练和识别的样本是否有物理机制可以支撑,能否作为 “判据” 使用是地震学界比较关心的问题。在深度学习中使用的波形功率谱并不是直接作为判据使用,而是作为训练(学习)和测试样本使用,应用深度学习技术从波形功率谱中学习出爆破和地震的频谱特征,这些被学习到的特征是一种概率分布,而这些学习到的概率分布才是本文中应用到的判据,但是深度学习作为一种黑箱算法很难从物理机制上阐述出这些特征(概率分布)的物理意义,这确实是深度学习解释中的一个短板。但是这并不影响波形功率谱可以作为训练(学习)和测试样本使用,只要应用测试样本进行测试的准确率比较高,就可以证明从训练样本中是可以学习出爆破和地震的特征规律的。本文试验结果也表明,应用波形功率谱进行训练和测试,可以准确区分爆破和地震事件,因而将波形功率谱作为训练和测试样本是可行的。
-
图 2 本文应用的残差网络模型
图中省略了4层卷积核为64和128的卷积层,加上全连接层及分类器层,共计14层,图中上方数字2×2为卷积核大小,下方数字为卷积核的数量
Figure 2. The residual network model applied in this paper
The four convolutional layers with 64 and 128 convolution kernels was omitted;coupled with the fully connected layer and the classifier layer,there are 14 layers in total。2×2 on the upper in the figures is the size of the convolution kernel,and on the bottom is the number of the convolution kernel
图 6 基于台站记录的试验结果
图(a)和(b)为第一组试验中的100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(c)和(d)分别表示第二组试验中100次随机子试验和1 000次随机子试验,每次子试验从地震和爆破中分别抽取 27和46次事件进行训练,余下的事件作为预测
Figure 6. Test results based on station records
Figs. (a) and (b) are the results for the 100 random subtests and 1 000 random subtests in the first group, each subtest selects 20 events from earthquakes and explosions for training,and the remaining events are used as predictions;Figs. (c) and (d) are the results for 100 random subtests and 1 000 random subtests in the second group,each subtest selects 27 and 46 events from earthquakes and explosions for training,and the remaining events are used as predictions
图 7 基于事件的100次随机子试验结果
图(a)为第一组试验中的100次随机子试验,每次的子试验从地震和爆破中分别抽取20次事件进行训练,余下的事件作为预测;图(b)为第二组试验中的100次随机子试验,每次子试验从地震和爆破中分别抽取27和46次事件进行训练,余下的事件作为预测。图中红、蓝线条分别代表基于50%,60%台站记录被正确判别为识别标准(基于事件)的识别率
Figure 7. Results of 100 random subtests based on the events
Figs. (a) and (b) represent 100 random subtests in the first group and the second group,respectively. Fig. (a) indicates that each subtest takes 20 events from the blasting and earthquakes for training,and the remaining events are used as predictions;Fig. (b) indicates that each subtest takes 46 and 27 events from the blasting and earthquakes for training,and the remaining events are used as predictions.
表 1 各卷积层输入及输出的通道数量
Table 1 The number of channels for input and output of each convolution layer
卷积层 输入通道数 输出通道数 卷积层 输入通道数 输出通道数 卷积层 输入通道数 输出通道数 1 1 8 6 32 64 11 256 256 2 8 16 7 64 64 12 256 512 3 16 16 8 64 128 13 512 512 4 16 32 9 128 128 14 全连接 5 32 32 10 128 256 表 2 基于事件的3组试验结果对比
Table 2 Comparison of the three groups of event-based test results
试验组 随机子
试验次数基于50%记录被正确
判别的平均识别率基于50%记录被正确
判别的地震识别率基于50%记录被正确
判别的爆破识别率平均值 最大值 最小值 平均值 最大值 最小值 平均值 最大值 最小值 第一组 100 97.7% 100% 93.5% 99.4% 100% 97.1% 96.9% 100% 91.8% 1 000 97.6% 100% 92.5% 99.3% 100% 97.1% 96.8% 100% 90.4% 第二组 100 98.4% 100% 95.9% 98.7% 100% 96.3% 98.3% 100% 93.6% 1 000 98.3% 100% 94.6% 98.8% 100% 90.5% 98.1% 100% 93.6% 留一交叉验证 97.3% 96.3% 97.8% -
郝春月,郑重,张爽. 2012. 玉树地震前后当地的噪声变化研究[J]. 地球物理学进展,27(6):2418–2428. doi: 10.6038/j.issn.1004-2903.2012.06.016 Hao C Y,Zheng Z,Zhang S. 2012. Research about noise variation around YUS station before and after the Yushu earthquake[J]. Progress in Geophysics,27(6):2418–2428 (in Chinese).
刘晗,张建中. 2014. 微震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展,29(4):1708–1714. doi: 10.6038/pg20140429 Liu H,Zhang J Z. 2014. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J]. Progress in Geophysics,29(4):1708–1714 (in Chinese).
山世光,阚美娜,刘昕,刘梦怡,邬书哲. 2016. 深度学习:多层神经网络的复兴与变革[J]. 科技导报,34(14):60–70. Shan S G,Kan M N,Liu X,Liu M Y,Wu S Z. 2016. Deep Learning:The revival and transformation of multi layer neural networks[J]. Science&Technology Review,34(14):60–70 (in Chinese).
孙志军,薛磊,许阳明,王正. 2012. 深度学习研究综述[J]. 计算机应用研究,29(8):2806–2810. doi: 10.3969/j.issn.1001-3695.2012.08.002 Sun Z J,Xue L,Xu Y M,Wang Z. 2012. Overview of Deep Learning[J]. Application Research of Computers,29(8):2806–2810 (in Chinese).
王婷婷,边银菊,张博. 2013. 地震和爆破的综合识别方法研究[J]. 地球物理学进展,28(5):2433–2443. doi: 10.6038/pg20130522 Wang T T,Bian Y J,Zhang B. 2013. The comprehensive identification methods between earthquakes and explosions[J]. Progress in Geophysics,28(5):2433–2443 (in Chinese).
杨宏,贾维敏. 2000. 基于神经网络的综合评判在核爆模式识别中的应用[J]. 核电子学与探测技术,20(4):279–283. doi: 10.3969/j.issn.0258-0934.2000.04.009 Yang H,Jia W M. 2000. Recognition of underground nuclear explosion and natural earthquake based on neural network[J]. Nuclear Electronics&Detection Technology,20(4):279–283 (in Chinese).
AitLaasri E H,Akhouayri E S,Agliz D,Atmani A. 2013. Seismic signal classification using multi-layer perceptron neural network[J]. Int J Comput Appl,79(15):35–43.
Baer M,Kradolfer U. 1987. An automatic phase picker for local and teleseismic events[J]. Bull Seismol Soc Am,77(4):1437–1445.
Bengio Y,Simard P,Frasconi P. 2002. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Trans Neural Netw,5(2):157–166.
Bennett T J,Murphy J R. 1986. Analysis of seismic discrimination capabilities using regional data from western United States events[J]. Bull Seismol Soc Am,76(4):1069–1086.
Dahl G E, Yu D, Deng L, Acero A. 2011. Large vocabulary continuous speech recognition with context-dependent DBN-HMMS[C]//IEEE International Conference on Acoustics Speech and Signal Processing. Prague: IEEE: 4688−4691.
Esposito A M,Giudicepietro F,Scarpetta S,D’Auria L,Marinaro M,Martini,M. 2006. Automatic discrimination among landslide,explosion-quake,and microtremor seismic signals at Stromboli Volcano using neural networks[J]. Bull Seismol Soc Am,96(4A):1230–1240. doi: 10.1785/0120050097
Falsaperla S,Graziani S,Nunnari G,Spampinato S. 1996. Automatic classification of volcanic earthquakes by using multi-layered neural networks[J]. Nat Hazards,13(3):205–228.
He K M, Zhang X Y, Ren S Q, Sun J. 2016. Deep residual learning for image recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE: 770−778.
Hong T K. 2013. Seismic discrimination of the 2009 North Korean nuclear explosion based on regional source spectra[J]. J Seismol,17(2):753–769. doi: 10.1007/s10950-012-9352-1
Kingma D P, Ba J. 2015. Adam: A method for stochastic optimization[C]//Proceedings of the 3rd International Conference for Learning Representations. San Diego: The Institute for Catastrophic Loss Redu Ction.
Kohavi R. 1995. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. Montreal: Morgan Kaufmann Publishers Inc, 14: 1137−1143.
Kortström J,Uski M,Tiira T. 2016. Automatic classification of seismic events within a regional seismograph network[J]. Comput Geosci,87:22–30. doi: 10.1016/j.cageo.2015.11.006
Krizhevsky A, Sutskever I, Hinton G E. 2012. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc, 1097−1105.
Kuyuk H S,Yildirim E,Dogan E,Horasan G. 2011. An unsupervised learning algorithm:Application to the discrimination of seismic events and quarry blasts in the vicinity of Istanbul[J]. Nat Hazards Earth Syst Sci,11(1):93–100. doi: 10.5194/nhess-11-93-2011
Lee H, Largman Y, Pham P, Ng A Y. 2009. Unsupervised feature learning for audio classification using convolutional deep belief networks[C]//Proceedings of the 22nd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc: 1096−1104.
Rabin N,Bregman Y,Lindenbaum O,Ben-Horin Y,Averbuch A. 2016. Earthquake-explosion discrimination using diffusion maps[J]. Geophys J Int,207(3):1484–1492. doi: 10.1093/gji/ggw348
Ren S Q,He K M,Girshick R,Sun J. 2015. Faster R-CNN:Towards real-time object detection with region proposal networks[J]. IEEE Trans Pattern Anal Mach Intell,39(6):1137–1149.
Reynen A,Audet P. 2017. Supervised machine learning on a network scale:Application to seismic event classification and detection[J]. Geophys J Int,210(3):1394–1409. doi: 10.1093/gji/ggx238
Riggelsen C,Ohrnberger M. 2014. A machine learning approach for improving the detection capabilities at 3C seismic stations[J]. Pure Appl Geophys,171(3/4/5):395–411. doi: 10.1007/s00024-012-0592-3
Simonyan K, Zisserman A. 2015. Very deep convolutional networks for large-scale image recognition[C]//Proceedings of the 3rd International Conference for Learning Representations. San Diego: The Institute for Catastrophic Loss Redu Ction.
Stevenson P R. 1976. Microearthquakes at Flathead Lake,Montana:A study using automatic earthquake processing[J]. Bull Seismol Soc Am,66(1):61–80.
Stump B W,Hedlin M A H,Pearson D C,Hsu V. 2002. Characterization of mining explosions at regional distances[J]. Rev Geophys,40(4):2–1.
Szegedy C, Liu W, Jia Y Q, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. 2015. Going deeper with convolutions[C]//IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE: 1−9.
Tiira T. 1995. Discrimination of nuclear explosions and earthquakes from teleseismic distances with a local network of short period seismic stations using artificial neural networks[J]. Phys Earth Planet Inter,97(1/2/3/4):247–268.
Vallejos J A,McKinnon S D. 2013. Logistic regression and neural network classification of seismic records[J]. Int J Rock Mech Min Sci,62:86–95. doi: 10.1016/j.ijrmms.2013.04.005
Wiemer S. 2000. Mapping and removing quarry blast events from seismicity catalogs[J]. Bull Seismol Soc Am,90(2):525–530. doi: 10.1785/0119990104
-
期刊类型引用(25)
1. 彭登靖,王泽兰,马敏伟,马达. 昭通巡龙强夯土非天然地震记录特征及识别研究. 地震科学进展. 2024(03): 187-192 .  百度学术
百度学术
2. 贾漯昭,孟令媛,闫睿. 深度学习在地震监测预报中的应用进展. 地震研究. 2024(03): 336-349 .  百度学术
百度学术
3. 王婷婷,边银菊,任梦依,杨千里,侯晓琳. 地震事件分类识别软件. 地震. 2024(02): 104-119 .  百度学术
百度学术
4. 彭登靖. 基于卷积神经网络的天然地震和非天然地震识别. 高原地震. 2024(02): 36-40 .  百度学术
百度学术
5. 沈婕,朱景宝,缪发军,宋晋东,李山有. 基于残差神经网络的天然地震与非天然地震信号分类. 地震工程与工程振动. 2024(05): 13-25 .  百度学术
百度学术
6. 曾晓燕,邱强,蒋策,周少辉,梁明,熊成. 基于卷积神经网络的地震与爆破识别模型及其在广东地区的初步应用. 地震学报. 2024(06): 1002-1013 .  本站查看
本站查看
7. 谭笑枫,李夕海,牛超,曾小牛,李鸿儒,刘天佑. 基于MVIDA算法和MS-SE-Res Net的次声事件分类方法(英文). Applied Geophysics. 2024(04): 667-679+878-879 .  百度学术
百度学术
8. 张帆,杨晓忠,王树波. 基于LSTM神经网络的地震事件分类. 计算机应用与软件. 2023(04): 75-79 .  百度学术
百度学术
9. 章宇成,华卫. 白鹤滩水库库区基于深度学习的震相拾取与地震定位. 地震. 2023(01): 137-151 .  百度学术
百度学术
10. 王泽兰. 昭通巡龙测震台强夯土事件与微震波形特征分析. 高原地震. 2023(03): 16-20+34 .  百度学术
百度学术
11. 邵永谦,王国成,彭钊,于海英,王鹏,王成睿. 基于标准时频变换的上海地区地震与爆破识别. 华北地震科学. 2022(02): 48-55 .  百度学术
百度学术
12. 田宵,汪明军,张雄,王向腾,盛书中,吕坚. 基于多输入卷积神经网络的天然地震和爆破事件识别. 地球物理学报. 2022(05): 1802-1812 .  百度学术
百度学术
13. 郑杰,文畅,谢凯,盛冠群. 参数优选残差网络下的井震联合反演方法. 电子测量技术. 2022(12): 168-174 .  百度学术
百度学术
14. 吴涛,庞聪,江勇,丁炜,廖成旺. 基于随机子空间和Ada Boost集成学习的地震事件性质辨识研究. 地球物理学进展. 2022(03): 981-988 .  百度学术
百度学术
15. 刘涛,戴志军,陈苏,傅磊. 基于深度学习的地震震级分类. 地震学报. 2022(04): 656-664 .  本站查看
本站查看
16. 孟娟,张家声,李亚南. 基于改进EWT和LogitBoost集成分类器的地震事件分类识别算法. 地震工程学报. 2022(05): 1233-1242 .  百度学术
百度学术
17. 隗永刚,蒋长胜. 人工智能技术在地震减灾应用中的研究进展. 地球物理学进展. 2021(02): 516-524 .  百度学术
百度学术
18. 程先琼,蒋科植. 基于深度降噪自编码神经网络的中国大陆地壳厚度反演. 地震学报. 2021(01): 34-47+136 .  本站查看
本站查看
19. 谭笑枫,李夕海,刘继昊,李广帅,于晓彤. 基于一维卷积神经网络的化爆和地震次声分类. 应用声学. 2021(03): 457-467 .  百度学术
百度学术
20. 周少辉,蒋海昆,曲均浩,李健,郭宗斌,郑旭. 爆破、塌陷识别研究进展综述. 中国地震. 2021(02): 508-522 .  百度学术
百度学术
21. 唐婷婷,余思,陈江贻. 天然地震与人工爆破特征识别研究综述. 地震科学进展. 2021(09): 385-394 .  百度学术
百度学术
22. 张帆,杨晓忠,吴立飞,韩晓明,王树波. 基于短时傅里叶变换和卷积神经网络的地震事件分类. 地震学报. 2021(04): 463-473+533 .  本站查看
本站查看
23. Ce Jiang,Lihua Fang,Liping Fan,Boren Li. Comparison of the earthquake detection abilities of PhaseNet and EQTransformer with the Yangbi and Maduo earthquakes. Earthquake Science. 2021(05): 425-435 .  必应学术
必应学术
24. 高家乙,刘晓锋,闫睿. 河南平顶山平煤矿区天然地震、爆破、塌陷时频特征分析. 地震地磁观测与研究. 2020(03): 67-74 .  百度学术
百度学术
25. 杨千里,王婷婷,边银菊. 基于广义S变换的地震与爆炸识别. 地震学报. 2020(05): 613-628+508 .  本站查看
本站查看
其他类型引用(12)





 下载:
下载: