Influence of permanent displacement of ground motion on seismic response of structures
-
摘要: 本文推导了基于位移激励计算单自由度体系拟速度谱公式，通过构造的脉冲位移时程对公式精度进行了验证；之后利用小波变换去除强震记录噪声而保留地震动永久位移，再基于去趋势项方法和滤波方法去除永久位移后，计算拟速度谱。算例结果表明：短周期段内，不保留永久位移的位移激励拟速度谱值与保留永久位移的位移激励拟速度谱值相差很小；中长周期段内，不保留永久位移的位移激励拟速度谱值总体上小于保留永久位移的位移激励拟速度谱值，且不保留永久位移时，滤波方法引起的拟速度谱降幅大于去趋势项方法所引起的拟速度谱降幅。因此，基于位移激励计算中长周期结构的地震反应时，应保留地震动永久位移，或基于去趋势项方法去除永久位移。Abstract: When calculating the seismic response of a structure based on the displacement excitation, the displacement excitation is obtained by integration of the velocity, which is obtained by integration of the acceleration records. At the same time, the acceleration noise must be removed. However, limited by the method for eliminating noise from acceleration records, the permanent displacement of the ground motion in the near-fault earthquake acceleration records is often weakened or even eliminated. This makes it impossible for researchers to judge the effect of permanent displacement of ground motion on the seismic response of structures excited by displacement. In this paper, the authors deduce the pseudo-velocity spectra formula of single degree of freedom system based on displacement excitation, verify the accuracy of the formula with the constructed pulse displacement time history, and then analyze the effect of the permanent displacement of the ground motion on the pseudo-velocity spectra. Firstly, the noise is executed on the acceleration records via wavelet transform, and gound motion with permanent displacement is remained. And then the permanent displacement is wiped out using reducing trend item method or filtering method from those records. Those excitations are used to calculate pseudo-velocity spectra. The results show that in short period, the pseudo-velocity spectra are similar whether ground motions contain the permanent displacement or not; in medium-long period, the pseudo-velocity spectra excited by non-permanent displacement excitation are lower than those by displacement excitation with permanent displacement, and this kind of difference are enlarged when the filtering method is used. Therefore, for seismic design of long-period structures, the ground motion with permanent ground displacement excitation should be used, or reducing trend item method is used to wipe out permanent displacement.
-
引言
结构地震反应是结构抗震设计的基础，其准确性决定了结构是否具有良好的抗震性能。计算结构地震反应时，可以使用加速度激励，也可以使用位移激励。但是研究人员发现，对同一个结构进行地震反应分析时，采用位移激励和加速度激励获得的结构反应会相差很大 （Xu et al，2020）。由于基于加速度激励计算结构地震反应的方法已经很成熟，应用广泛，同时研究人员认为基于位移激励计算结构地震反应方法存在缺陷，这两方面均限制了位移激励在结构分析中的应用 （Tsai，1998；Hızal，Turan，2017）。
早期曾出现过的位移记录仪，因受频带窄、功耗大的限制现已很少使用，而现有的地震动监测设备是以加速度或速度的形式记录地震动。因此，利用位移激励计算结构地震反应时，使用的位移激励大多是由加速度积分两次计算所得。受加速度仪的精度和工作状态的影响，加速度记录中不仅包含真实的地震动信号，同时还包含着环境和仪器噪声信号，甚至在近场地震动记录中，还存在由于地面变形过大而引起的加速度记录基线偏移现象。无论是记录中的噪声还是加速度基线偏移，虽然对加速度记录的影响并不大，但对积分后的位移影响很大（Boore，2001；Boore et al，2002），而且对加速度记录直接积分所得的位移激励不能用于结构地震反应分析。
在地震波到达强震记录仪之前，仪器输出的加速度理论上应为零，但受背景噪音和仪器噪声的影响，强震记录仪输出的加速度记录的震前部分并不为零，而且这些噪声在加速度记录中是持续存在的。针对消除加速度记录中的噪声，研究人员进行了大量的研究，例如：Chanerley和Alexander （2010）利用双正交小波基对强震动加速度记录降噪；Li等（2005）利用地震波形态的差异，借用基于数学形态学发展起来的形态滤波方法压制地震记录中的野值脉冲噪声。此外，加速度记录中的噪声也可以通过高通滤波的方式进行消除。王体强等（2019）对比时域与频域积分方法对加速度积分位移结果精度的影响时，指出高通滤波是获取稳定、准确的动态位移响应的可靠途径。高通滤波后，加速度记录中的长周期信号被滤除，意味着加速度记录中不再包含与长周期信号对应的永久地面位移，由此记录积分获得的位移记录也不再包含与长周期信号对应的永久地面位移。Chiu （1997）采用高通滤波方法对加速度记录进行处理，校正后的记录只包含部分地面永久位移。周雍年等（1997）建议估计地面永久位移时，不能对积分位移曲线进行高通滤波。为避免使用滤波方法处理加速度记录，同时又能保证积分后的地面位移与实际地面运动相一致，研究人员常以地面速度为突破口（谢俊举等，2013；周宝峰等，2013），将微小的地面速度添加到加速度积分后的速度记录中，再对速度记录积分获得位移，使得地震结束时地面速度为零，以此完成地面位移修正。例如：Iwan等（1985）进行地面位移的基线调整时，将加速度时程分为开始段、强震段和结束段，其中基线偏移发生在强震段和结束段，在结束段基线偏移量趋近于常数；王国权等对Iwan等（1985）的校正方法进行改进，提出单段校正法（v0校正方法），认为速度时程的尾段呈线性趋势，将获得的速度时程尾部斜率添加到加速度记录中，再对加速度积分以此获得位移 （Wang et al，2003；王国权，周锡元，2004）；张海明和陈晓非（2004）对单段校正法加以改进，提出了选择最佳时段拟合速度尾端的方法；陈勇等（2007）提出以位移时程末端平稳为原则确定最优速度尾段斜率；荣棉水等（2014）在此基础上进一步优化地面速度校正方法，引入“时移斜率比”、“拟合段标准差”和“位移尾段均方差”来确定速度时程尾部拟合段的取值范围（王国权，周锡元，2004）。上述研究关注的焦点是尽可能获得真实的地面位移，部分研究人员通过计算获得的地面位移与GPS同震记录位移进行对比（荣棉水等，2014），以验证所采用方法的可靠性。基于这些方法获得的位移在结构地震反应分析中的应用并不多，例如，惠迎新和王克海（2015）采用基线校正法获得位移激励，并用于近断层大跨度桥梁结构的地震反应分析中。在结构地震反应分析中，大多数位移激励是对加速度记录滤波后再积分获得，通过设定滤波参数，实现修正的积分速度和积分位移在地震动停止时数值为零，或者直接对加速度积分获得位移，再去除位移时程的地面位移趋势项，使地震动停止时位移为零（李建波等，2004；李吉涛，杨庆山，2010）。由这些方法获得的位移记录，只包含部分或完全不包含地面永久位移，以此位移记录作为地震动分析的结构反应时，无法体现地面永久位移对结构反应的影响。
为探讨位移激励时地震动永久位移对结构地震反应的影响，本文拟推导基于位移激励的单自由度体系拟速度谱计算公式，并将利用加速度记录积分获得的位移时程作为地震动输入计算拟速度谱，对比由位移激励计算的拟速度谱与由加速度激励计算的拟速度谱的差别，以分析位移激励时地震动永久位移对结构地震反应的影响规律。
1. 基于位移激励的拟速度反应谱
单自由度体系的振动模型如图1所示。假设全部质量m集中在质点处，基于相对坐标建立的单自由度体系动力平衡方程为
$m\ddot \nu {\text{＋}} {\rm{2}}\xi \omega \dot \nu {\text{＋}} k\nu {\text{＝}} {\text{－}} m{\ddot u_{\rm{g}}}{\text{，}}$
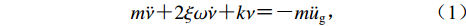
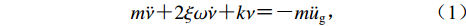
(1) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
利用以Duhamel （杜哈梅）积分形式表示式（1）中的结构反应，可获得单自由度体系的相对速度反应谱，即
${S_{\text{ν}} }\!\!\!\!{\text{（}}\xi {{{\text{，}}\!\!\overline T{\text{）}}\!\!\!\! {\text{＝}} }}{\left| {\int_0^t {{{\ddot u}_{\rm{g}}}\!\!\!\!{\text{（}}\tau{\text{）}}\!\!\!\!{{\rm{e}}^{ {\text{－}} \xi \omega \!\!{\text{（}}t {\text{－}} \tau{\text{）}}}}\!\!\!\!\!\!{\text{［}}\!\cos {\omega _{\rm{d}}}\!\!\!\!{\text{（}}t {\text{－}} \tau{\text{）}} \!\!\!\!{\text{－}} \frac{\xi }{{\sqrt {1 {\text{－}} {\xi ^2}} }}\sin {\omega _{\rm{d}}}\!\!\!\!{\text{（}}t {\text{－}} \tau{\text{）}}\!\!\!\!\!\!{\text{］}}\!\!{\rm{d}}\tau } } \right|_{\max }}{\text{，}}$
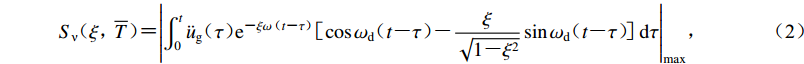
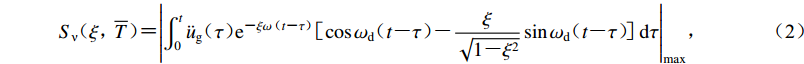
(2) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
当结构阻尼比ζ较小时，可进一步将拟速度反应谱改写为
${S_{{\rm{p}}{\text{ν}} }}{\rm{\!\!\!\!{\text{（}}\!}}\xi {{{\text{，}}\!\!\!\overline T\!{\text{）}}\!\!\!\! {\text{＝}} }}{\left| {\int_0^t {{{\ddot u}_{\rm{g}}}\!\!\!\!{\text{（}}\!\tau\!{\text{）}}\!\!\!\!{{\rm{e}}^{{\text{－}}\xi \omega \!\!\!\!{\text{（}}\!t{\text{－}}\tau\!{\text{）}}\!\!\!\!}}\cos {\omega _{\rm{d}}}\!\!\!\!{\text{（}}\!t{\text{－}}\tau\!{\text{）}}\!\!\!\!{\rm{d}}\tau } } \right|_{\max }}{\text{，}}\!\!\!$
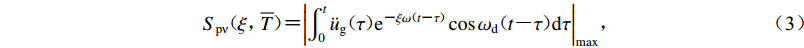
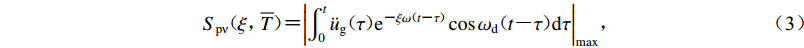
(3) 对式（3）进行积分，将式中的地震动由加速度形式转换为位移形式，可得
${S_{{\rm{p}}{\text{ν}} }}{\rm{\!\!\!\!{\text{（}}\!}}\xi {{{\text{，}}\!\!\!\overline T\!{\text{）}}\!\!\!\! {\text{＝}} }}{\left| {{{\dot u}_{\rm{g}}}\!\!\!\!{\text{（}}\!t\!{\text{）}}\!\!\!\!{\text{－}}{u_{\rm{g}}}\!\!\!\!{\text{（}}\!t\!{\text{）}}\!\!\!\!\xi \omega {\text{－}}{\omega ^2}\int_0^t {{u_{\rm{g}}}\!\!\!\!{\text{（}}\!\tau\!{\text{）}}\!\!\!\!{{\rm{e}}^{{\text{－}}\xi \omega \!\!\!\!{\text{（}}\!t{\text{－}}\tau\!{\text{）}}\!\!\!\!}}\cos {\omega _{\rm{d}}}\!\!\!{\text{［}}\!2\theta {\text{＋}} \!\!\!\!{\text{（}}\!t{\text{－}}\tau\!{\text{）}}\!\!\!\!\!\!{\text{］}}\!\!{\rm{d}}\tau } } \right|_{\max }}{\text{，}}$
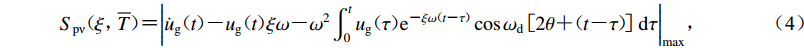
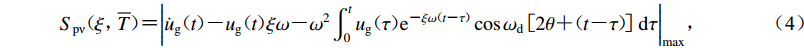
(4) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
从式（3）到式（4）的转换过程可知，式（4）仍是计算单自由度体系的拟速度反应谱公式，该反应谱是以位移激励形式的地震动作为输入计算。鉴于地震动可以通过加速度、速度和位移三种形式表示，这意味着对于同一地震动，利用式（3）和式（4）计算所得的拟速度反应谱相同。
2. 位移激励拟速度谱与加速度激励拟速度谱对比
以钟形脉冲为地震动输入，验证式（4）的准确性。位移脉冲时程的数学表达式为（荣棉水等，2007）
$a\!\!\!\!{\text{（}}\!t \!{\text{）}}\!\!\!\! {\text{＝}} {a_0}{{\rm{e}}^{{\text{－}}\gamma {{\!\!\!\!{\text{（}}\!t{\text{－}}{t_0}\!{\text{）}}\!\!\!\!}^2}}}{\text{，}}\;A\!\!\!\!{\text{（}}\!\omega \!{\text{）}}\!\!\!\! {\text{＝}} \sqrt {\frac{{\rm{{\text{π}} }}}{\gamma }} {a_0}\exp \left[ {{\text{－}}\left({\frac{{{\omega ^2}}}{{4\gamma }} {\text{＋}} {\rm{i}}\omega {t_0}} \right)} \right]{\text{，}}$
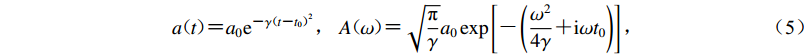
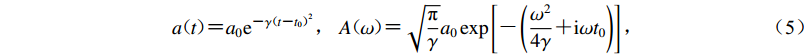
(5) 式中，a（t）为钟形脉冲时程，A（ω）为其傅里叶谱，γ为钟形脉冲形状参数，t0为脉冲峰值点对应的时刻，a0为地面位移峰值。本文分别取a0＝5 cm，γ＝2 000，t0＝0.1 s。钟形脉冲的位移时程、速度时程和加速度时程如图2所示，利用式（3）和式（4）分别计算位移钟形脉冲的拟速度谱，如图3所示。从中可以看出，通过位移激励计算的拟速度谱与通过加速度激励计算的拟速度谱相差很小，由此可知，本文中给出的公式可以用于计算单自由度体系的拟速度谱。
3. 地震动永久位移的影响
分析地震动永久位移对位移激励下结构反应的影响时，所使用的位移激励是由强震记录积分两次得到。选用四条近场地震动记录进行单自由度体系拟位移谱的对比，地震动信息列于表1。分别按照三种方法处理加速度积分位移，具体如下：① 方法一，保留地震动永久位移。首先，对强震记录进行小波变换，分解近似系数和细节系数后，利用阈值将信噪比较小的系数置零，完成记录噪声清除；然后，调整底层近似系数，使积分后位移曲线的末端趋势与时间轴平行，完成地震动加速度重构；最后，再对加速度进行积分，此时获得的位移包含永久地面位移；② 方法二，以去趋势项方法去除地震动永久位移。利用最小二乘法获得永久地面位移曲线，再从位移中去除永久位移；③ 方法三，通过滤波方法去除地震动永久位移。对四条重构的地震动加速度，积分前采用高通滤波方法进行滤波（高通滤波的截止频率为0.1 Hz），使积分后的位移在地震终止时刻位移为零。重构的加速度激励和由三种方法获得的位移激励如图4所示。按照震中距小于30 km，脉冲指数大于0.85 （Baker，2007），在速度时程前几秒形成的脉冲峰值速度大于30 m/s的原则，选取近场地震动的强震记录。以这种方式选取的地震动能体现永久位移在地震发生时形成的过程。四条地震动的永久位移峰值由5.0 cm增大至22. 3 cm，该值用来代表地面位移峰值大小对结构反应的影响。
表 1 地震动信息Table 1. Ground motion information序号 地震 发震时间
年−月−日ML 观测位置 断层距/km 峰值加速度
/（cm·s−2）1 美国加州卡莱克西科市
（Calexico）地震2010−04−04 7.2 卡莱克西科市欧姆林（Omlin）
公寓邦德角（Bond’s Corner）35.7 120.32 2 美国加州卡莱克西科市
（Calexico）地震2010−04−04 7.2 卡莱克西科市消防站 23.1 266.45 3 新西兰地震 2010−09−03 7.0 新西兰林肯作物与食物研究中心 6.3 426.80 4 美国加州里奇克莱斯特
（Ridgecrest）地震2019−07−05 7.1 加州里奇克莱斯特395号
公路/布朗路桥22.3 237.74 ![]()
图 4 加速度激励、无永久位移的位移激励及包含永久位移的位移激励（a） 欧姆林公寓邦德角记录到的2010年4月4日美国卡莱克西科市地震；（b） 卡莱克西科市消防站记录到的2010年4月4日美国卡莱克西科市地震：（c） 林肯作物与食物研究中心记录到的2010年9月3日新西兰地震；（d） 里奇克莱斯特395号公路/布朗路桥记录到的2019年7月5日美国里奇克莱斯特地震Figure 4. Acceleration excitations，displacement excitations containing permanent ground displacement and displacement excitations without permanent ground displacement（a） Calexico earthquake in USA on 4 April 2010 recorded by the Bond’s Corner of Omlin Residence；（b） Calexico earthquake in USA on 4 April 2010 recorded by the Calexico Fire Station；（c） New Zealand earthquake on 3 September 2010 recorded by the Lincoln Crop and Food Research；（d） Ridgecrest earthquake in USA on 5 July 2019 recorded by the Ridgecrest-Highway 395/Brown Road Bridge对表1中的加速度记录去除噪声，将处理后的加速度与其积分位移绘于图4。以不大于加速度峰值的5%为限制条件，从图4中选取包含强震段且总长为40 s的地震动作为输入，计算拟速度反应谱，以台站名称进行区分的计算结果如图5所示。
![]()
图 5 不同点位的拟速度谱对比图（单自由度体系阻尼比ζ＝0.02）（a） 欧姆林公寓邦德角；（b） 卡莱克西科市消防站；（c） 林肯作物与食物研究中心；（d） 里奇克莱斯特395号公路/布朗路桥Figure 5. Comparing of pseudo-velocity spectra （damping ratio ζ＝0.02）for different sites（a） The Bond’s Corner，Omlin Residence；（b） The Calexico Fire Station；（c） The Lincoln Crop and Food Research； （d） The Ridgecrest-Highway 395/Brown Road Bridge从图5可以看出：短周期段内由加速度激励、保留地震动永久位移的位移激励与去除永久位移的位移激励计算得到的拟速度谱相差不大；中长周期段内，加速度激励拟速度谱与保留地震动永久位移的位移激励拟速度谱相差不大，去趋势项方法去除永久位移的位移激励拟速度谱值较以滤波方法去除永久位移的位移激励拟速度谱值大。进一步对比可以看出：在0—1 s周期段内，四种方法获得的拟速度谱曲线形状基本相同，不同方法的谱值最大相差不超过10%；在1—3 s周期段内，由三种位移激励获得的拟速度谱曲线形状基本相同，但在少数的周期处会出现加速度激励与位移激励的拟速度谱相差较大的现象，最大相差近20%；在3—6 s周期段内，以滤波方法去除永久位移的位移激励拟速度谱曲线，与其它三种方法的拟速度谱曲线在形状上相差较大，在较多的周期处出现低于加速度激励拟速度谱值且幅值相差超过20%的现象；在整个周期段内以去趋势项方法去除永久位移的位移激励拟速度谱的幅值与保留永久位移的位移激励拟速度谱相比，会低5%左右。
清除地震动记录噪声时，多采用高通滤波或带通滤波。尽管这两种方法应用方便，但处理后的地震动不再包含永久位移和部分低频信号。受滤波器精度的限制，滤波过程中不仅截止频率之外的信号被清除，与截止频率相近的信号也会被削弱。从本文的拟速度谱对比可以看出，这种削弱减小了位移激励下的结构反应，此时，这些地震动不宜用于位移激励地震反应分析。对于去趋势项方法而言，清除永久位移可以转换为对速度记录进行纠正，通常速度修正的幅值并不大，从拟速度谱对比可以看出，这种纠正方法对拟速度谱的影响较滤波方法对拟速度谱的影响低。
上述拟速度谱对比分析表明，利用位移激励计算中长周期结构的地震反应时，应保留地震动永久位移。
4. 讨论与结论
基于位移激励计算结构地震反应分析方法是结构抗震分析与设计理论的重要组成部分，但加速度记录中的噪声对积分后位移记录的精度影响很大，进而影响到结构地震反应的分析结果。针对降低噪声对结构地震反应精度影响的研究一直受到关注。地震工程领域的研究人员提出一些修正地面位移时程的方法，如广泛应用的滤波方法和基线校正方法，使积分位移与实际地面位移趋势相同，实现噪声清除。滤波方法改变了地震动的自身特性，但目前绝大多数文献仍基于此方法计算位移激励。基线校正方法在位移激励动力分析中应用很少，例如惠迎新和王克海（2015）指出利用基线校正方法校正后的加速度积分位移可以作为激励计算结构动力反应，除此之外很少有文献涉及。本文分析位移激励下结构反应影响因素时，对比了以这两种方法处理地震动所引入的误差。本文在阐明地面永久位移对结构反应的影响规律时，首先给出了以地面速度和地面位移作为输入荷载计算拟速度反应谱的公式，确保由加速度激励和位移激励得到的反应谱是相同的，消除了输入荷载类型不同情况下反应谱会出现的差别。算例结果表明，经基线校正后的位移激励获得的反应谱与加速度激励获得的反应谱相差不大，这与惠迎新和王克海（2015）的结论相一致。同时，本文发现滤波后的加速度积分位移用于计算短周期结构地震反应时，其结构反应与加速度激励时的结构反应相差不大，但用于计算中长周期结构地震反应时，结构反应会明显降低，此时不建议采用该方法获得位移激励。
-
![]()
图 4 加速度激励、无永久位移的位移激励及包含永久位移的位移激励
（a） 欧姆林公寓邦德角记录到的2010年4月4日美国卡莱克西科市地震；（b） 卡莱克西科市消防站记录到的2010年4月4日美国卡莱克西科市地震：（c） 林肯作物与食物研究中心记录到的2010年9月3日新西兰地震；（d） 里奇克莱斯特395号公路/布朗路桥记录到的2019年7月5日美国里奇克莱斯特地震
Figure 4. Acceleration excitations，displacement excitations containing permanent ground displacement and displacement excitations without permanent ground displacement
（a） Calexico earthquake in USA on 4 April 2010 recorded by the Bond’s Corner of Omlin Residence；（b） Calexico earthquake in USA on 4 April 2010 recorded by the Calexico Fire Station；（c） New Zealand earthquake on 3 September 2010 recorded by the Lincoln Crop and Food Research；（d） Ridgecrest earthquake in USA on 5 July 2019 recorded by the Ridgecrest-Highway 395/Brown Road Bridge
![]()
图 5 不同点位的拟速度谱对比图（单自由度体系阻尼比ζ＝0.02）
（a） 欧姆林公寓邦德角；（b） 卡莱克西科市消防站；（c） 林肯作物与食物研究中心；（d） 里奇克莱斯特395号公路/布朗路桥
Figure 5. Comparing of pseudo-velocity spectra （damping ratio ζ＝0.02）for different sites
（a） The Bond’s Corner，Omlin Residence；（b） The Calexico Fire Station；（c） The Lincoln Crop and Food Research； （d） The Ridgecrest-Highway 395/Brown Road Bridge
表 1 地震动信息
Table 1 Ground motion information
序号 地震 发震时间
年−月−日ML 观测位置 断层距/km 峰值加速度
/（cm·s−2）1 美国加州卡莱克西科市
（Calexico）地震2010−04−04 7.2 卡莱克西科市欧姆林（Omlin）
公寓邦德角（Bond’s Corner）35.7 120.32 2 美国加州卡莱克西科市
（Calexico）地震2010−04−04 7.2 卡莱克西科市消防站 23.1 266.45 3 新西兰地震 2010−09−03 7.0 新西兰林肯作物与食物研究中心 6.3 426.80 4 美国加州里奇克莱斯特
（Ridgecrest）地震2019−07−05 7.1 加州里奇克莱斯特395号
公路/布朗路桥22.3 237.74 
下载: 导出CSV
-
陈勇,陈鲲,俞言祥. 2007. 用集集主震记录研究近断层强震记录的基线校正方法[J]. 地震工程与工程振动,27(4):1–7. Chen Y,Chen K,Yu Y X. 2007. Base line correction method for near-fault accelerograms using Chi-Chi main shock record[J]. Earthquake Engineering and Engineering Vibration,27(4):1–7 (in Chinese).
惠迎新,王克海. 2015. 基于多点激励位移输入模型的跨断层桥梁地震动输入方法[J]. 东南大学学报(自然科学版),45(3):557–562. Hui Y X,Wang K H. 2015. Earthquake motion input method for bridges crossing fault based on multi-support excitation displacement input model[J]. Journal of Southeast University (Natural Science Edition)
,45(3):557–562 (in Chinese). 李建波,陈健云,林皋. 2004. 相互作用分析中地震动输入长周期校正研究[J]. 大连理工大学学报,44(4):550–555. Li J B,Chen J Y,Lin G. 2004. Study of long-period correction of seismic accelerogram for dynamic interaction analysis[J]. Journal of Dalian University of Technology,44(4):550–555 (in Chinese).
李吉涛,杨庆山. 2010. 地震波基线漂移的处理方法[J]. 北京交通大学学报,34(1):95–99. Li J T,Yang Q S. 2010. A correction method for baseline drift of seismic wave[J]. Journal of Beijing Jiaotong University,34(1):95–99 (in Chinese).
荣棉水,李小军,卢滔. 2007. 局部地形对入射P波谱特性的影响分析[J]. 西北地震学报,29(4):297–302. Rong M S,Li X J,Lu T. 2007. Effect analysis of topography on the spectrum property of incident P waves[J]. Northwestern Seismological Journal,29(4):297–302 (in Chinese).
荣棉水,彭艳菊,喻畑,杨宇. 2014. 近断层强震观测记录基线校正的优化方法[J]. 土木工程学报,47(增刊2):300–306. Rong M S,Peng Y J,Yu T,Yang Y. 2014. Optimized baseline correction method for the near-fault observation strong motion records[J]. China Civil Engineering Journal,47(S2):300–306 (in Chinese).
王国权,周锡元. 2004. 921台湾集集地震近断层强震记录的基线校正[J]. 地震地质,26(1):1–14. Wang G Q,Zhou X Y. 2004. Baseline correction of near fault ground motion recordings of the 1999 Chi-Chi,Taiwan earthquake[J]. Seismology and Geology,26(1):1–14 (in Chinese).
王体强,王永志,袁晓铭,汤兆光,王海,段雪锋. 2019. 基于振动台试验的加速度积分位移方法可靠性研究[J]. 岩土力学,40(增刊1):565–573. Wang T Q,Wang Y Z,Yuan X M,Tang Z G,Wang H,Duan X F. 2019. Reliability analysis of acceleration integral displacement method based on shaking table tests[J]. Rock and Soil Mechanics,40(S1):565–573 (in Chinese).
谢俊举,温增平,高孟潭. 2013. 利用强震数据获取汶川地震近断层地面永久位移[J]. 地震学报,35(3):369–379. Xie J J,Wen Z P,Gao M T. 2013. Recovery of co-seismic deformation from strong motion records during the Wenchuan earthquake[J]. Acta Seismologica Sinica,35(3):369–379 (in Chinese).
张海明, 陈晓非. 2004. 根据数字强震加速度记录恢复位移波形的方法: 以1999年9月21日台湾集集地震为例[C]//中国大陆地震学与地球内部物理学研究进展: 庆贺曾融生院士八十寿辰. 北京: 地震出版社: 694–707. Zhang H M, Chen X F. 2004. The method of recovering displacement waveforms based on digital strong motion records: Take 1999·9·21 Chi-Chi earthquake for example[C]//Advances in Seismology and Physics of Earth’s Interior in China: In Honor of Academician Zeng Rongsheng’s 80th Birthday. Beijing: Seismological Press: 694–707 （in Chinese）.
周宝峰,于海英,温瑞智,谢礼立. 2013. 一种识别永久位移的新方法[J]. 土木工程学报,46(增刊2):135–140. Zhou B F,Yu H Y,Wen R Z,Xie L L. 2013. A new way of permanent displacement identification[J]. China Civil Engineering Journal,46(S2):135–140 (in Chinese).
周雍年,章文波,于海英. 1997. 数字强震仪记录的长周期误差分析[J]. 地震工程与工程振动,17(2):1–9. Zhou Y N,Zhang W B,Yu H Y. 1997. Analysis of long-period for accelerograms recorded by digital seismographs[J]. Earthquake Engineering and Engineering Vibration,17(2):1–9 (in Chinese).
Baker J W. 2007. Quantitative classification of near-fault ground motions using wavelet analysis[J]. Bull Seismol Soc Am,97(5):1486–1501. doi: 10.1785/0120060255
Boore D M. 2001. Effect of baseline corrections on displacements and response spectra for several recordings of the 1999 Chi-Chi,Taiwan,earthquake[J]. Bull Seismol Soc Am,91(5):1199–1211.
Boore D M,Stephens C D,Joyner W B. 2002. Comments on baseline correction of digital strong-motion data:Examples from the 1999 Hector Mine,California,earthquake[J]. Bull Seismol Soc Am,92(4):1543–1560. doi: 10.1785/0120000926
Chanerley A A,Alexander N A. 2010. Obtaining estimates of the low-frequency ‘fling’,instrument tilts and displacement timeseries using wavelet decomposition[J]. Bull Earthq Eng,8(2):231–255. doi: 10.1007/s10518-009-9150-5
Chiu H C. 1997. Stable baseline correction of digital strong-motion data[J]. Bull Seismol Soc Am,87(4):932–944.
Hızal C,Turan G. 2017. Importance of static correction and damping in the analysis of a cable-stayed bridge subjected to displacement loading[J]. J Bridge Eng,22(6):04017009. doi: 10.1061/(ASCE)BE.1943-5592.0001041
Iwan W D,Moser M A,Peng C Y. 1985. Some observations on strong-motion earthquake measurement using a digital accelerograph[J]. Bull Seismol Soc Am,75(5):1225–1246.
Li Q,Wang R Q,Huang W F,Zheng G J. 2005. Method for morphological filtering in seismic data processing[J]. Petrol Sci,2(4):20–29.
Tsai H C. 1998. Modal superposition method for dynamic analysis of structures excited by prescribed support displacements[J]. Comput Struct,66(5):675–683. doi: 10.1016/S0045-7949(97)00108-9
Wang G Q,Boore D M,Igel H,Zhou X Y. 2003. Some observations on colocated and closely spaced strong ground-motion records of the 1999 Chi-Chi,Taiwan,earthquake[J]. Bull Seismol Soc Am,93(2):674–693. doi: 10.1785/0120020045
Xu G L,Zhang L X,Bai Y S,Sun H. 2020. Method for solving dynamic equilibrium equations based on displacement excitation[J]. Earthq Eng Eng Vib,19(2):423–433. doi: 10.1007/s11803-020-0571-0
-
期刊类型引用(2)
1. 李艳华，宋廷苏，王林建，刘观. 永久位移型地震动对建筑隔震设计影响初探. 建筑结构. 2023(11): 110-115+102 . 
百度学术
2. 张宁，徐国林. 基于Hi-net速度记录计算地震反应谱. 地震工程与工程振动. 2022(01): 243-249 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 1542
- HTML全文浏览量: 517
- PDF下载量: 63
- 被引次数: 4
