Study on 2D in-plane HVSR simulation and application with transverse inhomogeneous body scattering
-
摘要: 为分析场地的横向不均匀性对水平竖向谱比HVSR曲线产生的显著影响，本文基于Sánchez-Sesma等提出的扩散场方法，通过计算总波场格林函数虚部对二维沉积地形上的HVSR曲线进行模拟。格林函数虚部则通过刚度矩阵和平面内斜线格林函数采用间接边界元方法进行求解。对二维沉积地形和相应的一维层状半空间的HVSR曲线进行了参数分析，着重讨论了沉积地形的形状、相对计算点位置等因素对HVSR曲线的影响规律。结果表明：沉积地形内外材料阻抗比对HVSR曲线的影响最为显著；随着沉积地形内外材料阻抗差异和沉积侧界面坡度的增大，沉积地形上HVSR曲线的第一峰值点的频率显著增大至相应层状半空间结果的3.3倍，同时HVSR曲线的形态呈现出平台现象；随着计算点到沉积边界距离的减小，HVSR曲线高频段幅值相对较大。根据本文得到的局部地形对HVSR曲线的影响规律，在进行场地勘探时可采用HVSR方法初步确定局部地形的分布位置以降低勘探成本。Abstract: In order to analyze the significant influence of lateral inhomogeneity of site on horizontal-to-vertical spectral ratio (HVSR) curves, the diffuse field approach proposed by Sánchez-Sesma et alwas adopted to simulate the HVSR curves of 2-D sediment topography by calculating the imaginary part of Green’s functions of total wave field. The imaginary part of Green’s functions was solved by the dynamic stiffness matrix and in-plane inclined Green’s functions based on the indirect boundary element method (IBEM). The HVSR curves of 2-D sediment topographies and corresponding 1-D layered half-space were compared, the influences of sediment topography shapes and the relative position of calculation points on the HVSR curve were discussed in detail. The results show that the effect of impedance ratio between inside and outside materials of sediment topography on HVSR is the most significant; With the increase of the impedance ratio and the slopes of the interface on the sediment side, the frequencies of the first peak of HVSR curves increase significantly, which can be up to 3.3 times of the corresponding layered half-space results, simultaneously, platform emerges on HVSR curves; Amplitudes of HVSR curves in high frequency band increase with the decrease of distances from the calculation points to the sediment boundary. According to the results obtained in this study, the HVSR method can be used to preliminarily determine the place where local sediment topography exists. From this aspect, the cost of regional geophysical investigation can be reduced visibly via HVSR method.
-
-
![]()
图 2 层状半空间中沉积内部中心点x＝0 m （a） 和非中心点x＝16 m （b）的方向能量密度随深度变化情况
Figure 2. Energy fluctuation of center point x＝0 m （a） and non-central point x＝16 m （b）in depth direction inside the alluvial canyon in layered half-space
![]()
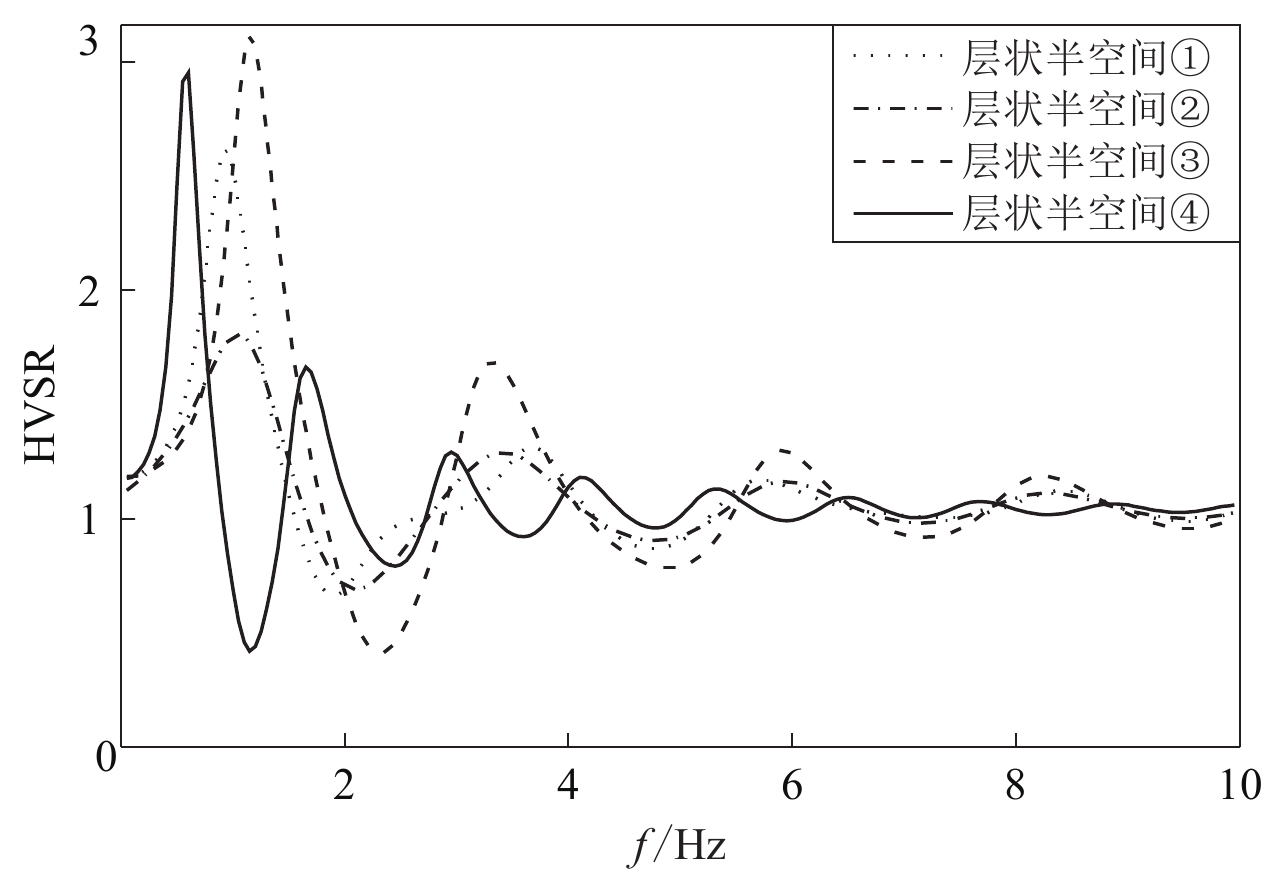
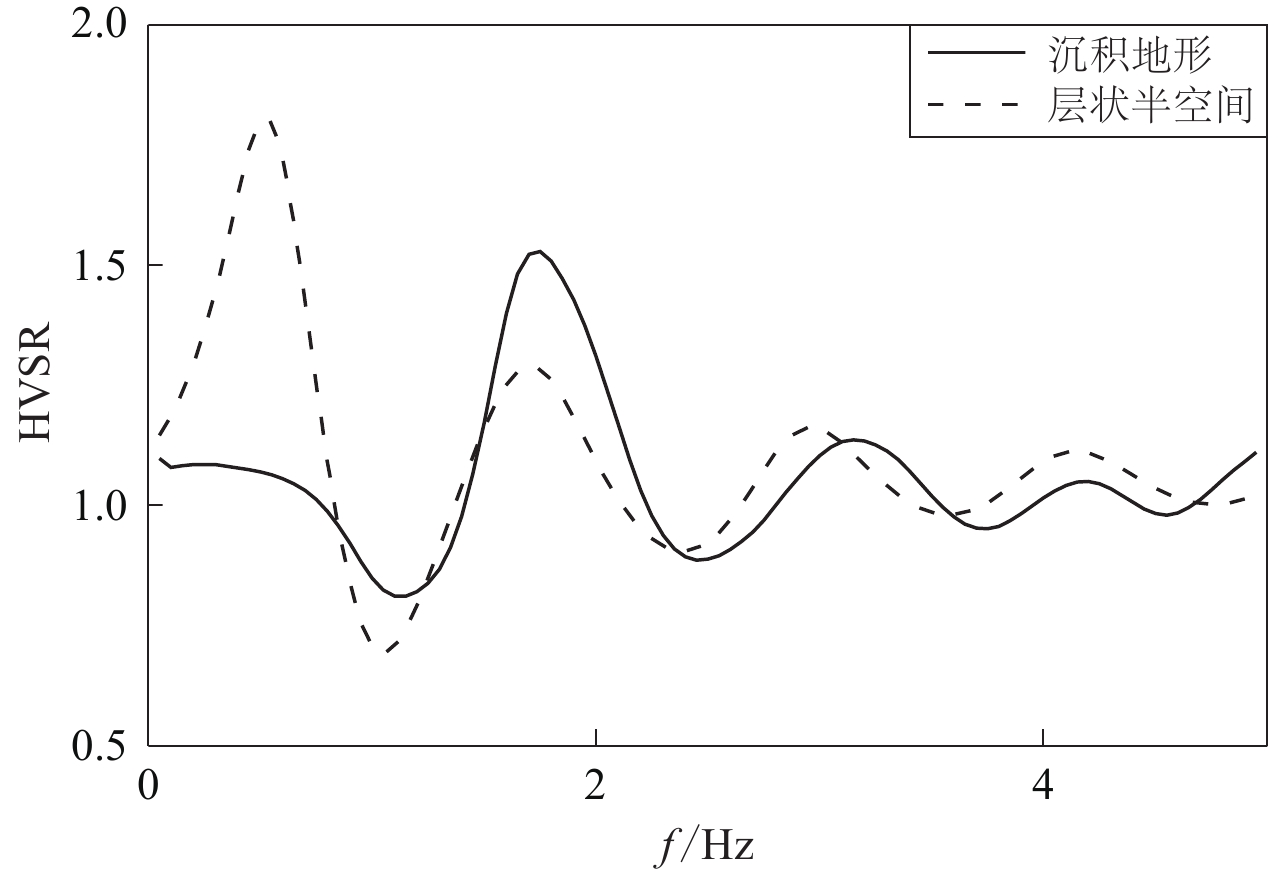
图 3 采用本文方法得到的层状半空间HVSR曲线与Sánchez-Sesma等（2011）结果对比
Figure 3. Comparisons of the result of layered half-space HVSR curves in this method with Sánchez-Sesma et al （2011）
![]()
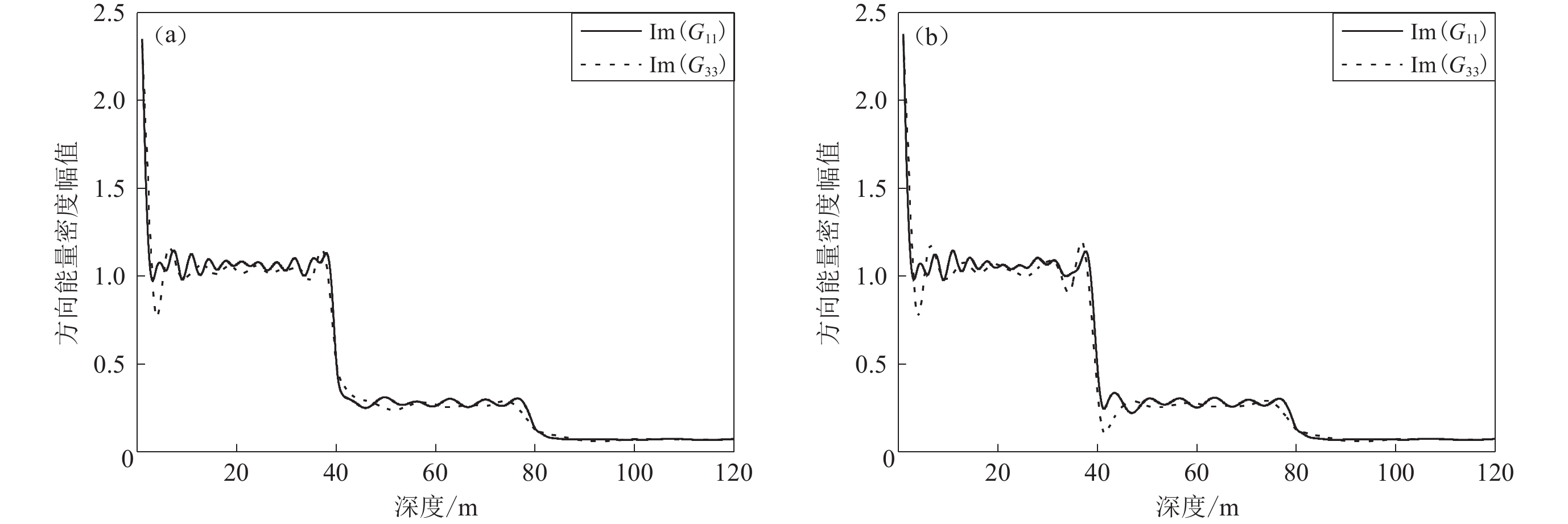
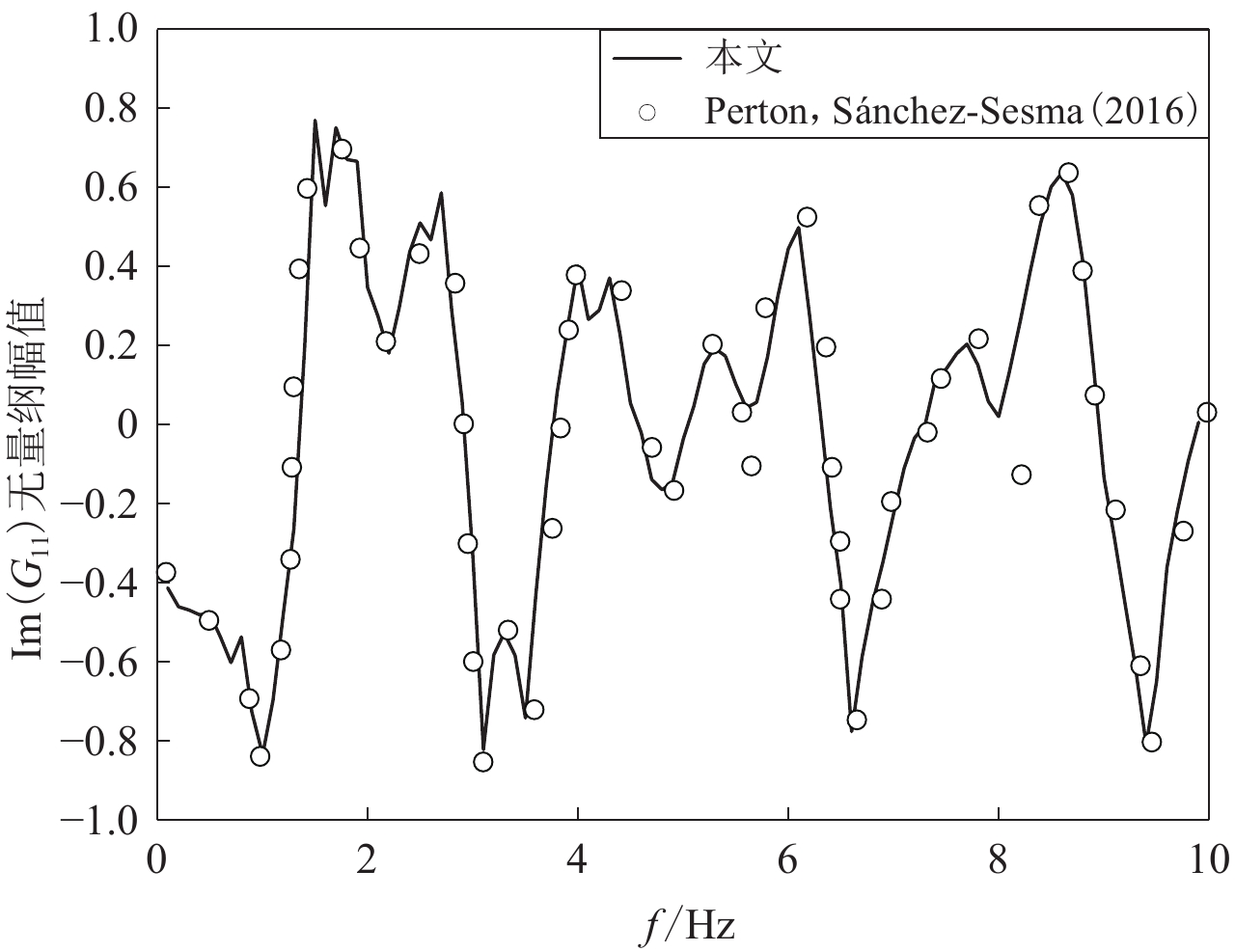
图 4 二维平面内采用本文方法得到的沉积地形上格林函数张量与Perton和Sánchez-Sesma （2016）的结果对比
Figure 4. Comparisons of the result of Green's function tensor on sedimentary topography in this method with Perton and Sánchez-Sesma （2016）
![]()
图 5 梯形沉积地形计算模型图
Figure 5. Calculation model graph of trape-zoidal sedimentary topography
![]()
图 6 层状半空间①—④ （a−d）计算模型图
Figure 6. Calculation model graph of layered half-spaces ①—④ （a−d）
![]()
图 8 沉积地形与相应层状半空间的HVSR曲线
Figure 8. HVSR curves of sedimentary topography and corresponding layered half-space
![]()
图 9 沉积地形（a）和其对应的层状半空间（b）内不同沉积内外阻抗比的HVSR曲线
Figure 9. HVSR curves of the sedimentary materials with different impedance ratios for sedimentarytopography (a) and its corresponding layered half space (b)
![]()
图 10 沉积内外材料阻抗比为1∶2 （a）和1∶4 （b）时不同横向不均匀界面坡度的HVSR曲线
Figure 10. HVSRs of different laterally inhomogeneous interface slopes with impedance ratios 1∶2 （a） and 1∶4 （b） between inside and outside materials of sedimental topography
![]()
图 11 沉积表面不同相对位置x/a上的HVSR曲线
（a） 沉积内外材料阻抗比1∶2；（b） 沉积内外材料阻抗比1∶4
Figure 11. HVSR curves of the sedimentary materials with different positions x/a
（a） The impedance ratio of internal and external material is 1∶2；（b） The impedance ratio of internal and external material is 1∶4
表 1 层状半空间计算参数
Table 1 Calculation parameters of layered half space
剪切波速
vS/（m·s−1）泊松比ν 土层密度
ρ/（kg·m−3）阻尼比ζ 土层 70 0.496 1 200 0.05 基岩 1 000 0.333 2 500 0.05 
下载: 导出CSV
表 2 层状半空间不同阻抗比情况计算参数
Table 2 Parameters of different impedance ratios in layered half-space
剪切波速
vS/（m·s−1）泊松比
ν土层密度
ρ/（kg·m−3）阻尼比
ζ沉积土层① 140 0.496 1 200 0.05 沉积土层② 280 0.496 1 200 0.05 基岩半空间① 560 0.496 1 200 0.05 基岩半空间② 280 0.496 1 200 0.05
下载: 导出CSV
表 3 不同沉积内外材料阻抗比情况计算参数
Table 3 Parameters of the alluvial canyon materials with different impedance ratios
剪切波速
vS/（m·s−1）泊松比
ν土层密度
ρ/（kg·m−3）阻尼比
ζ沉积内部土层 140 0.496 1 200 0.05 外部土层① 280 0.496 1 200 0.05 外部土层② 420 0.496 1 200 0.05 外部土层③ 560 0.496 1 200 0.05 外部土层④ 700 0.496 1 200 0.05 基岩半空间 1 000 0.333 2 500 0.05
下载: 导出CSV
表 4 不同沉积形状情况沉积地形计算参数
Table 4 Parameters of the alluvial canyon materials with different topography shapes
剪切波速
vS/（m·s−1）泊松比
ν土层密度
ρ/（kg·m−3）阻尼比
ζ沉积内部土层 140 0.496 1 200 0.05 外部土层① 280 0.496 1 200 0.05 外部土层② 420 0.496 1 200 0.05 基岩半空间 1 000 0.333 2 500 0.05
下载: 导出CSV
-
林国良,张潜,崔建文,赵昆,杨黎薇. 2019. 利用地脉动HVSR研究2014年鲁甸6.5级地震场地效应[J]. 地震研究,42(4):531–537. doi: 10.3969/j.issn.1000-0666.2019.04.011 Lin G L,Zhang Q,Cui J W,Zhao K,Yang L W. 2019. Determining the site effects of the 2014 Ludian MS6.5 earthquake using HVSR microtremor method[J]. Journal of Seismological Research,42(4):531–537 (in Chinese).
卢育霞,刘琨,王良,魏来,李少华. 2017. 基于台阵记录的土层山体场地效应分析[J]. 地震学报,39(6):941–954. Lu Y X,Liu K,Wang L,Wei L,Li S H. 2017. Site effect of unconsolidated soil hill based on seismic array records[J]. Acta Seismologica Sinica,39(6):941–954 (in Chinese).
荣棉水,李小军,王振明,吕悦军. 2016. HVSR方法用于地震作用下场地效应分析的适用性研究[J]. 地球物理学报,59(8):2878–2891. doi: 10.6038/cjg20160814 Rong M S,Li X J,Wang Z M,Lü Y J. 2016. Applicability of HVSR in an analysis of site-effects caused by earthquakes[J]. Chinese Journal of Geophysics,59(8):2878–2891 (in Chinese).
荣棉水,符力耘,李小军. 2018. 基于单台加速度记录的混合全局优化HVSR反演场地浅层速度结构[J]. 地球物理学报,61(3):938–947. doi: 10.6038/cjg2018L0171 Rong M S,Fu L Y,Li X J. 2018. Inversion of site velocity structure using a hybrid global optimization algorithm based on HVSRs of accelerograms recorded by a single station[J]. Chinese Journal of Geophysics,61(3):938–947 (in Chinese).
王伟君,陈棋福,齐诚,谭毅培,张项,周青云. 2011. 利用噪声HVSR方法探测近地表结构的可能性和局限性:以保定地区为例[J]. 地球物理学报,54(7):1783–1797. doi: 10.3969/j.issn.0001-5733.2011.07.012 Wang W J,Chen Q F,Qi C,Tan Y P,Zhang X,Zhou Q Y. 2011. The feasibilities and limitations to explore the near-surface structure with microtremor HVSR method:A case in Baoding area of Hebei Province,China[J]. Chinese Journal of Geophysics,54(7):1783–1797 (in Chinese).
温瑞智,冀昆,任叶飞,王宏伟. 2015. 基于谱比法的我国强震台站场地分类[J]. 岩石力学与工程学报,34(6):1236–1241. Wen R Z,Ji K,Ren Y F,Wang H W. 2015. Site classification for strong earthquake stations in China using spectral ratio method[J]. Chinese Journal of Rock Mechanics and Engineering,34(6):1236–1241 (in Chinese).
Arai H,Tokimatsu K. 2004. S-wave velocity profiling by inversion of microtremor H/V spectrum[J]. Bull Seismol Soc Am,94(1):53–63. doi: 10.1785/0120030028
Chavez-Gárcía F J,Rodríguez M,Field E,Hatzfeld D. 1997. Topographic site effects:A comparison of two nonreference methods[J]. Bull Seismol Soc Am,87(6):1667–1673. doi: 10.1785/BSSA0870061667
Gosar A. 2007. Microtremor HVSR study for assessing site effects in the Bovec basin (NW Slovenia) related to 1998 MW5.6 and 2004 MW5.2 earthquakes[J]. Eng Geol,91(2/3/4):178–193.
Guéguen P,Cornou C,Garambois S,Banton J. 2007. On the limitation of the H/V spectral ratio using seismic noise as an exploration tool:Application to the Grenoble Valley (France),a small apex ratio basin[J]. Pure Appl Geophys,164(1):115–134. doi: 10.1007/s00024-006-0151-x
Kawase H,Sánchez-Sesma F J,Matsushima S. 2011. The optimal use of horizontal-to-vertical spectral ratios of earthquake motions for velocity inversions based on diffuse-field theory for plane waves[J]. Bull Seismol Soc Am,101(5):2001–2014. doi: 10.1785/0120100263
Matsushima S,Hirokawa T,De Martin F,Kawase H,Sánchez-Sesma F J. 2014. The effect of lateral heterogeneity on horizontal-to-vertical spectral ratio of microtremors inferred from observation and synthetics[J]. Bull Seismol Soc Am,104(1):381–393. doi: 10.1785/0120120321
Nakamura Y. 1989. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface[J]. Quarterly Reports Railway Tech Res Inst,30(1):25–33.
Napolitano F,Gvasi A,La Rocca M L,Guerra I,Scarpa R. 2018. Site effects in the Pollino region from the HVSR and polarization of seismic noise and earthquakes[J]. Bull Seismol Soc Am,108(1):309–321. doi: 10.1785/0120170197
Nogoshi M,Igarashi T. 1971. On the amplitude characteristics of microtremor:Part 2[J]. Seism Soc Jap,24:26–40.
Perton M,Sánchez-Sesma F J,Rodríguez-Castellanos A,Campillo M,Weaver R L. 2009. Two perspectives on equipartition in diffuse elastic fields in three dimensions[J]. J Acoust Soc Am,126(3):1125–1130. doi: 10.1121/1.3177262
Perton M,Sánchez-Sesma F J. 2016. Green's function calculation from equipartition theorem[J]. J Acoust Soc Am,140(2):1309–1318. doi: 10.1121/1.4961208
Perton M,Spica Z,Caudron C. 2018. Inversion of the horizontal-to-vertical spectral ratio in presence of strong lateral heterogeneity[J]. Geophys J Int,212(2):930–941. doi: 10.1093/gji/ggx458
Piña-Flores J,Perton M,García-Jerez A,Carmona E,Luzón F,Molina-Villegas J C,Sánchez-Sesma F J. 2017. The inversion of spectral ratio H/V in a layered system using the diffuse field assumption (DFA)[J]. Geophys J Int,208(1):577–588. doi: 10.1093/gji/ggw416
Sánchez-Sesma F J,Campillo M. 2006. Retrieval of the Green’s function from cross correlation:The canonical elastic problem[J]. Bull Seismol Soc Am,96(3):1182–1191. doi: 10.1785/0120050181
Sánchez-Sesma F J,Pérez-Ruiz J A,Luzón F,Campillo M,Rodríguez-Castellanos A. 2008. Diffuse fields in dynamic elasticity[J]. Wave Motion,45(5):641–654. doi: 10.1016/j.wavemoti.2007.07.005
Sánchez-Sesma F J,Rodríguez M,Iturrarán-Viveros U,Luzón F,Campillo M,Margerin L,García-Jerez A,Suarez M,Santoyo M A,Rodríguez-Castellanos A. 2011. A theory for microtremor H/V spectral ratio:Application for a layered medium[J]. Geophys J Int,186(1):221–225. doi: 10.1111/j.1365-246X.2011.05064.x
Sánchez-Sesma F J. 2017. Modeling and inversion of the microtremor H/V spectral ratio:Physical basis behind the diffuse field approach[J]. Earth Planets Space,69(1):92. doi: 10.1186/s40623-017-0667-6
Stanko D,Markušić S,Strelec S,Gazdek M. 2017. HVSR analysis of seismic site effects and soil-structure resonance in Varaždin city (North Croatia)[J]. Soil Dyn Earthq Eng,92:666–677. doi: 10.1016/j.soildyn.2016.10.022
Uebayashi H. 2003. Extrapolation of irregular subsurface structures using the horizontal-to-vertical spectral ratio of long-period microtremors[J]. Bull Seismol Soc Am,93(2):570–582. doi: 10.1785/0120020137
Uebayashi H,Kawabe H,Kamae K. 2012. Reproduction of microseism H/V spectral features using a three-dimensional complex topographical model of the sediment-bedrock interface in the Osaka sedimentary basin[J]. Geophys J Int,189(2):1060–1074. doi: 10.1111/j.1365-246X.2012.05408.x
Weaver R L. 1982. On diffuse waves in solid media[J]. J Acoust Soc Am,71(6):1608–1609. doi: 10.1121/1.387816
Weaver R L. 1985. Diffuse elastic waves at a free surface[J]. J Acoust Soc Am,78(1):131–136. doi: 10.1121/1.392576
Wolf J P. 1985. Dynamic Soil-Structure Interaction[M]. Englewood Cliffs: Prentice-Hall.
计量
- 文章访问数: 259
- HTML全文浏览量: 201
- PDF下载量: 42
