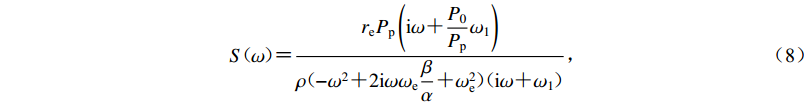The conjunct effects of ISO and CLVD sources in underground explosions on the spectral null in Rg waves
-
摘要: 本文利用地震面波激发理论计算了两种震源不同相对强度、相对埋深及源时间函数情况下的Rg波频谱,研究地下爆炸中各向同性(ISO)源和补偿线性矢量偶极(CLVD)源共同激发的Rg波信号低谷点特性。结果表明,由于两种震源相对强度、相对埋深及源频谱的影响,混合信号低谷点频率与单一CLVD源激发的信号有很大差异,因此实际地下爆炸中低谷点频率与CLVD源埋深不能单纯地满足理论的反比关系,直接用理论式估算地下爆炸埋深是不足的。Abstract: The compensated linear vector dipole (CLVD) source is usually induced by underground explosions and could lead to a null in the Rg spectra. There is a theoretical scale between the null frequency and the depth of the CLVD source. Therefore we can estimate the depth of underground explosions with the null frequency. However, this relationship is based on simply considering the CLVD source while the conjunct effects of ISO and CLVD sources are neglected. This study researches the conjunct effects of ISO and CLVD sources in underground explosions on the spectral null in Rg waves by numerical calculation of the Rg spectra with seismology theory of surface waves. The results indicate that the null in mixed signals is quite different from the results of single CLVD source. Thus the null frequency of Rg waves is not simply corresponding to the theoretical value in practical underground explosions and it is improper to estimate the depth of explosions by directly applying the theoretical formula.
-
Keywords:
- Rg wave /
- ISO source /
- CLVD source /
- spectral null
-
引言
地下爆炸中除各向同性(Isotropic,缩写为ISO)的爆炸源之外,通常还会产生补偿线性矢量偶极源(compensated linear vector dipole,缩写为CLVD)(Massé,1981),导致Rg波频谱出现低谷点(Patton,Taylor,1995),由于Lg波有相同的低谷点特性,这种现象支持了Lg波来自Rg-S散射的观点(Gupta et al,1992)。Aki和Richards (1980)的定量地震学理论表明,低谷点频率与CLVD源埋深存在定量关系,同时根据Gupta等(1997)对内华达试验场地下爆炸的统计,CLVD源埋深约为爆炸源埋深的1/3,因此利用Rg波低谷点频率可以估算地下爆炸埋深。但上述定量关系是针对均匀半空间泊松体介质和单一CLVD源推导出的,因此在应用于实际地下爆炸时存在一定的局限性。
鉴于Rg波低谷点对当量估算的重要作用,国内外科研人员对影响低谷点频率的因素开展了相关研究。何永锋等(2005)分析了不同介质速度模型中低谷点频率随CLVD源埋深的变化;徐恒垒等(2011)分析了地表起伏对低谷点位置的影响;Baker等(2012a,b)指出在内华达的低速介质中,不同源都有可能产生低谷点。这些结果表明在接近真实的地表介质中,低谷点频率与CLVD源埋深关系与理论值存在一定偏差。另一方面,由于上述研究关注的是介质模型的影响,因此只考虑了CLVD源的作用,而地下爆炸中ISO源和CLVD源都会激发Rg波,并且两者源频谱也存在差异(Mueller,Murphy,1971;Denny,Johnson,1991;Patton,Taylor,2011)。本文通过理论计算和分析ISO与CLVD源共同激发的Rg波归一化位移谱,研究了两种震源相对强度、埋深及源频谱对低谷点频率的影响,进一步阐明了低谷点的特性,对之后的地下爆炸埋深估算具有重要意义。
1. Rg波低谷点形成机理及混合信号激发模型
根据Aki和Richards(1980)的定量地震学理论,埋深为hd、矩张量为
${\boldsymbol{M}}_{ij} $ 的震源激发的瑞雷波垂向上的位移可以表示为$$ \begin{split} {u_{{{\textit{z}}}}}{\text{(}}r{\text{,}}\omega {\text{)}} {\text{=}} & \sum\limits_n {\frac{{{r_2}{\text{(}}{k_{{n}}}{\text{,}}{\textit{z}}{\text{,}}\omega {\text{)}}}}{{8{c_{{n}}}{U_{{n}}}I_1^{\text{R}}}}} \sqrt {\frac{2}{{{\text{π }}{k_{{n}}}r}}} \exp \Bigg[{\text{i}}\Bigg({k_{{n}}}r {\text{+}} \frac{{\text{π }}}{4}\Bigg)\Bigg] \Bigg\{{k_{{n}}}{r_{\text{1}}}{\text{(}}{h_{\text{d}}}{{{\text{)}}[}}{M_{{{xx}}}}{\text{co}}{{\text{s}}^{\text{2}}}\phi {\text{+}}{M_{{{xy}}}}{\text{sin2}}\phi {\text{+}}\\&{M_{{{yy}}}}{\text{si}}{{{n}}^{\text{2}}}\phi] {\text{+}} {\text{i}}\left[ {{{\left. {\frac{{{\text{d}}{r_1}}}{{{\text{d}}{\textit{z}}}}} \right|}_{{h_{\text{d}}}}} {\text{-}} {k_{{n}}}{r_2}{\text{(}}{h_{\text{d}}}{\text{)}}} \right][{M_{{{x{\textit{z}}}}}}\cos \phi {\text{+}} {M_{{{y{\textit{z}}}}}}\sin \phi ] {\text{+}} {\left. {\frac{{{\text{d}}{r_2}}}{{{\text{d}}{\textit{z}}}}} \right|_{{h_{\text{d}}}}}{M_{{{{\textit{z}}{\textit{z}}}}}}\Biggr\} \end{split} {\text{,}} $$ (1) 式中,uz(r,ω)为瑞雷波垂向位移,n为振型阶数,kn为波数,r1和r2分别为水平和垂直方向的位移本征函数,cn和Un为相应的相速度和群速度,I1R为能量积分,ϕ为方位角。
根据式(1),不考虑格林函数时,深度为h的CLVD源激发的瑞雷波垂向幅值为
$$ {M_{{\text{CLVD}}}}{\text{(}}\omega {\text{)}}\left\{ { - \frac{1}{2}k{r_1}{\text{(}}h{\text{)}} {\text{+}} {{\left. {\frac{{{\text{d}}{r_2}}}{{{\text{d}}{\textit{z}}}}} \right|}_h}} \right\} {\text{,}} $$ (2) 式中,MCLVD(ω)为CLVD源地震矩。
在均匀半空间中,本征位移函数为
$$ \left\{\begin{array}{l}{r}_{1}{\text{(}}{\textit{z}}{\text{)}}{\text{=}}{\text{exp}} {\text{(}}{-\omega {\eta }_{{\alpha}}{\textit{z}}}{\text{)}}{\text{+}}\dfrac{1}{2}\left(\dfrac{{c}^{2}}{{\beta }^{2}}{\text{-}}2\right){\rm{exp}}{\text{(}}{-\omega {\eta }_{{\beta}}{\textit{z}}}{\text{)}}{\text{,}}\\ {r}_{2}{\text{(}}{\textit{z}}{\text{)}}{\text{=}}c{\eta }_{{\alpha}}{\text{exp}}{\text{(}}{-\omega {\eta }_{{\alpha}}{\textit{z}}}{\text{)}}{\text{+}}\dfrac{1}{2c{\eta }_{{\beta}}}\left(\dfrac{{c}^{2}}{{\beta }^{2}}{\text{-}}2\right){\rm{exp}}{\text{(}}{-\omega {\eta }_{{\beta}}{\textit{z}}}{\text{)}}{\text{,}}\end{array} \right. $$ (3) 式中,
${\eta _\alpha } {\text{=}} \sqrt { {\text{(}}{c^{ - 2}} {\text{-}}{\alpha ^{ - 2}}} {\text{)}} $ ,${\eta _\beta } {\text{=}} \sqrt { {\text{(}}{c^{ - 2}} {\text{-}}{\beta ^{ - 2}}} {\text{)}} $ ,c=U,α和β分别为纵波和横波波速。将式(3)代入式(2),则有
$$\begin{split} &{M_{{\text{CLVD}}}}{\text{(}} \omega {\text{)}}\left\{ { - \frac{1}{2}k{r_1}{\text{(}}h{\text{)}} {\text{+}} {{\left. {\frac{{{\text{d}}{r_2}}}{{{\text{d}}{\textit{z}}}}} \right|}_{{h}}}} \right\} {\text{=}} \\& - {M_{{\text{CLVD}}}}{\text{(}}\omega {\text{)}}k\Biggl[ {\left(\frac{3}{2} {\text{-}} \frac{{{c^2}}}{{{\alpha ^2}}}\right){{\text{exp}} {\text{(}}{ - \omega {\eta _{{\alpha }}}h}} {\text{)}} }{ {\text{-}} \frac{3}{4}\left(2 {\text{-}} \frac{{{c^2}}}{{{\beta ^2}}}\right){{\text{exp}} {\text{(}}{ - \omega {\eta _{{\beta }}}h}}} {\text{)}} \Biggl] {\text{,}} \end{split}$$ (4) 泊松条件下,c=0.919 4β,代入式(4),并令其等于0,即Rg波位移谱中出现幅值为0的低谷点,则低谷点对应频率与CLVD源埋深满足
$$ {f_{{\text{null}}}} \approx \frac{\alpha }{{16h}} {\text{,}} $$ (5) 式中,fnull表示位移谱中低谷点对应的频率。
纯爆炸源情况下,假设其埋深为he,地震矩为MISO(ω),则激发的瑞雷波垂向幅值为(忽略格林函数)
$$ {M_{{\text{ISO}}}}{\text{(}} \omega {\text{)}}{\left\{ {k{r_1}{\text{(}}{h_{\text{e}}}{\text{)}} {\text{+}} \left. {\frac{{{\text{d}}{r_2}}}{{{\text{d}}{\textit{z}}}}} \right|} _{{h_{\text{e}}}}\right\}} {\text{=}}{M_{{\text{ISO}}}}{\text{(}} \omega {\text{)}}k\frac{{{c^2}}}{{{\alpha ^2}}}{{\text{exp}}{\text{(}}{ - \omega {\eta _{{\alpha}}}{h_{\text{e}}}}}{\text{)}} {\text{,}} $$ (6) 显然不存在幅值为0的低谷点。
结合式(4),(6)和(1),可得ISO和CLVD源共同作用时激发的基阶Rg波混合信号垂向幅值为
$$\begin{split} {u_{{{\textit{z}}}}}{\text{(}}r{\text{,}}\omega {\text{)}} {\text{=}}& \frac{{r_2{\text{(}}k{\text{,}}{\textit{z}}{\text{,}}\omega {\text{)}}}}{{8cUI_1^{}}}\sqrt {\frac{2}{{{\text{π }}kr}}} \exp \Bigg[{\text{i}}\Bigg(kr {\text{+}} \frac{{\text{π }}}{4}\Bigg)\Bigg] \Bigg\{ -\Bigg[{{\Bigg(\frac{3}{2} {\text{-}} \frac{{{c^2}}}{{{\alpha ^2}}}\Bigg){{\text{exp}} {\text{(}}{ - \omega {\eta _{{\alpha }}}h}}{\text{)}} }}\\& {{{\text{-}} \frac{3}{4}\Bigg(2 {\text{-}} \frac{{{c^2}}}{{{\beta ^2}}}\Bigg){{\text{exp}} {\text{(}}{ - \omega {\eta _{{\beta }}}h}}}{\text{)}} \Bigg]{M_{{\text{CLVD}}}}{\text{(}}\omega {\text{)}} {\text{+}} {M_{{\text{ISO}}}}{\text{(}} \omega {\text{)}}k\frac{{{c^2}}}{{{\alpha ^2}}}{{\text{exp}} {\text{(}}{ - \omega {\eta _{{\alpha}}}{h_{{{\rm{e}}}}}}}} {\text{)}}\Bigg\} {\text{.}}\end{split} $$ (7) 式(7)表明混合信号幅值受两种源相对强度、相对埋深和源频谱等因素的影响,可能会与单一CLVD源激发的信号有很大差异。
2. ISO和CLVD源共同作用对Rg波低谷点的影响
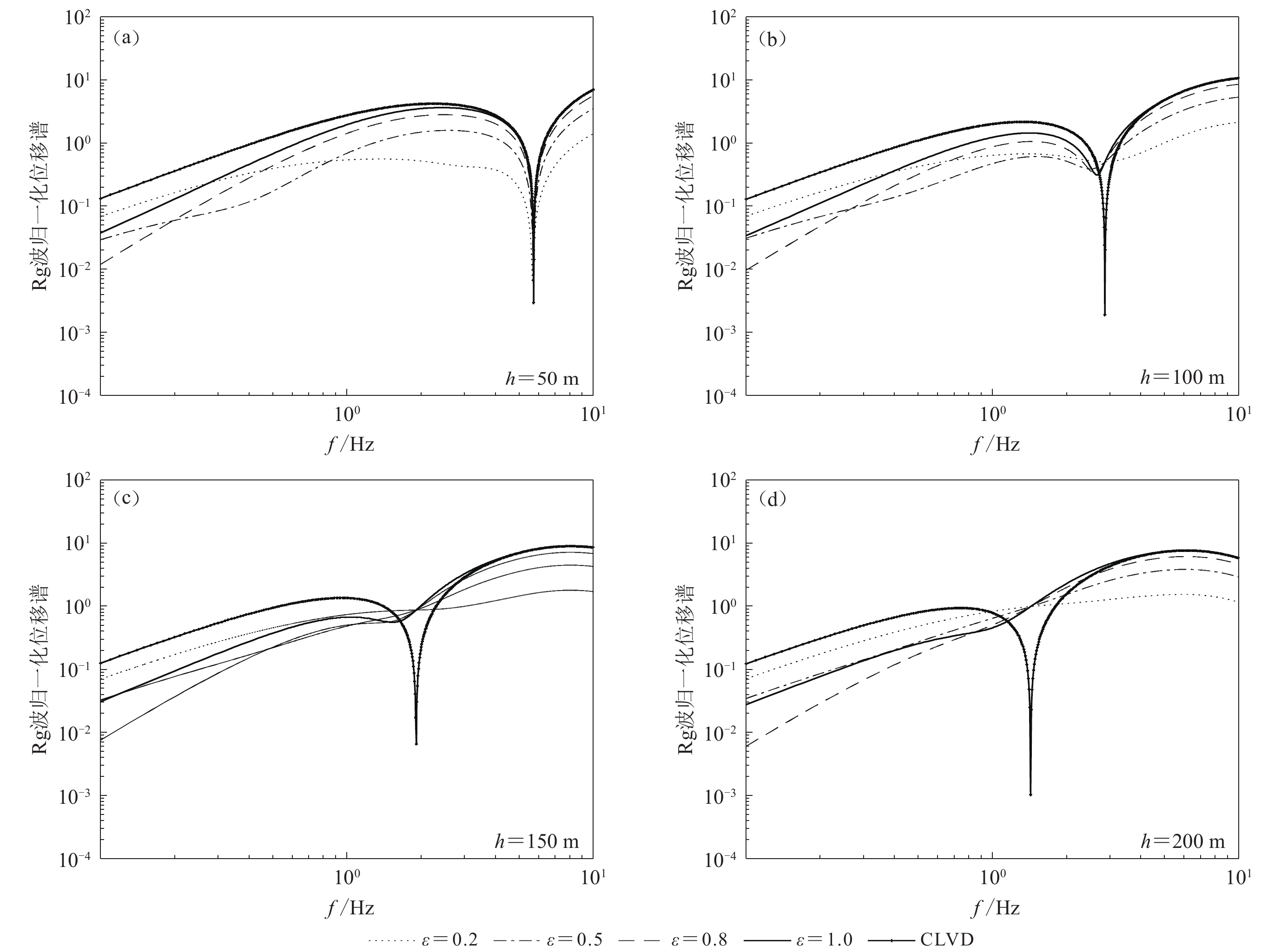
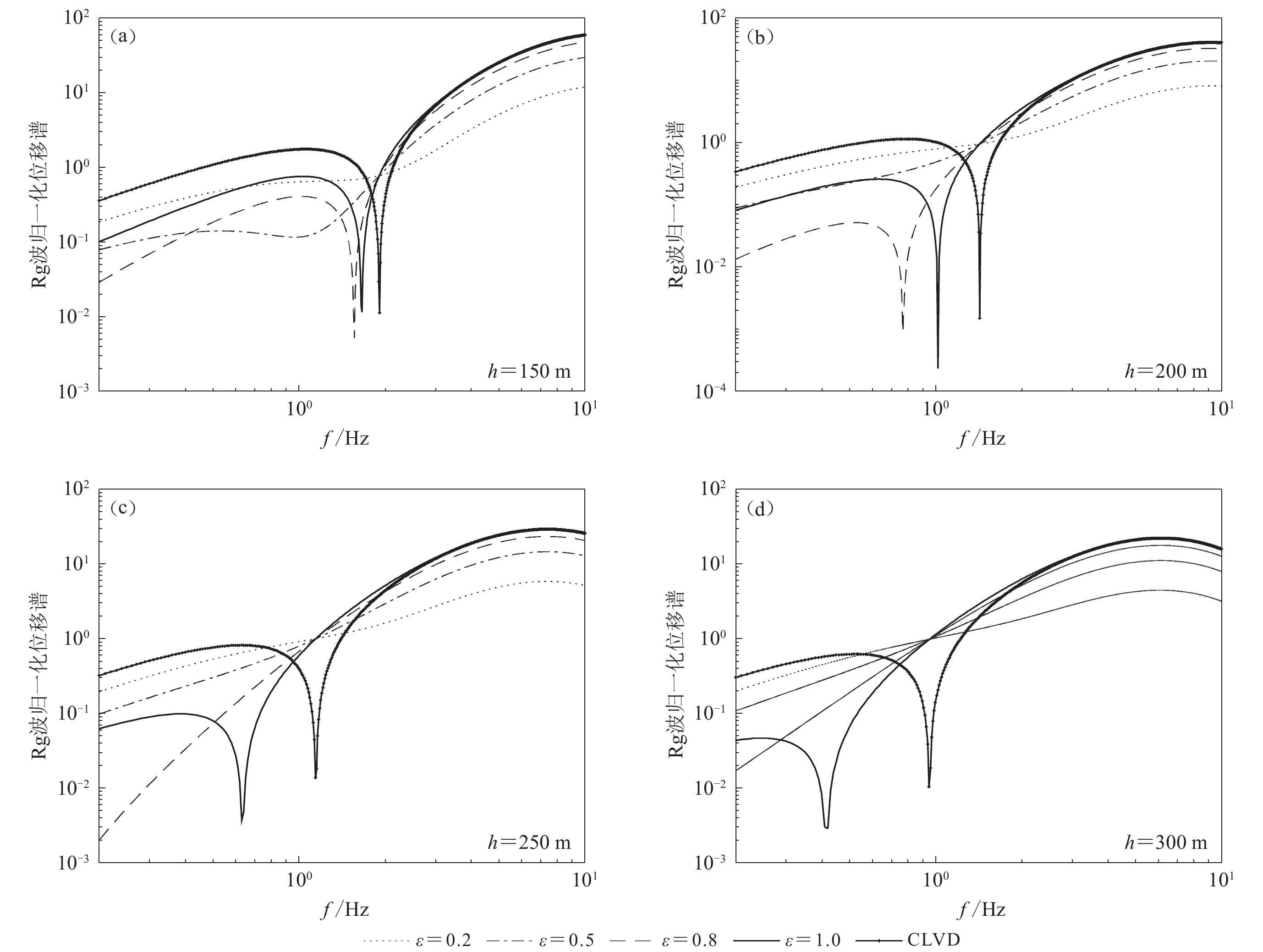
首先不考虑源频谱的差异,分析两种震源相对强度对低谷点的影响(假设两种源模型都为δ脉冲函数)。设ISO源埋深he为600 m (下同),CLVD源埋深h分别为100,150,200,300 m,P波波速为4.6 km/s,泊松比为0.25,记CLVD/ISO相对强度为ε,取值范围为0.2—1。利用式(7)得到震中距200 m处归一化的Rg波位移谱如图1所示(用纯ISO源激发的信号最大幅值归一化,下同),图中一并给出单一CLVD源激发的信号幅值谱。从图1中可以看出:两种震源共同作用时Rg波幅值整体降低,并非各自激发信号简单的叠加;CLVD源相对强度较小时混合信号没有低谷点,当低谷点存在时,低谷点频率fnull随相对强度ε的增大而增大,但是相对于单一CLVD源的情况,低谷点频率总体变小。
![]() 图 1 CLVD源埋深h为150 (a),200 (b),250 (c)和300 m (d)时不同相对强度下,ISO和CLVD源共同激发的Rg波归一化位移谱.ε为CLVD/ISO相对强度Figure 1. The normalized Rg spectra excited by conjunct sources of ISO and CLVD in different relative strengths at the CLVD source depths of 150 (a),200 (b),250 (c) and 300 m (d). ε is the relative strength of CLVD source to ISO source
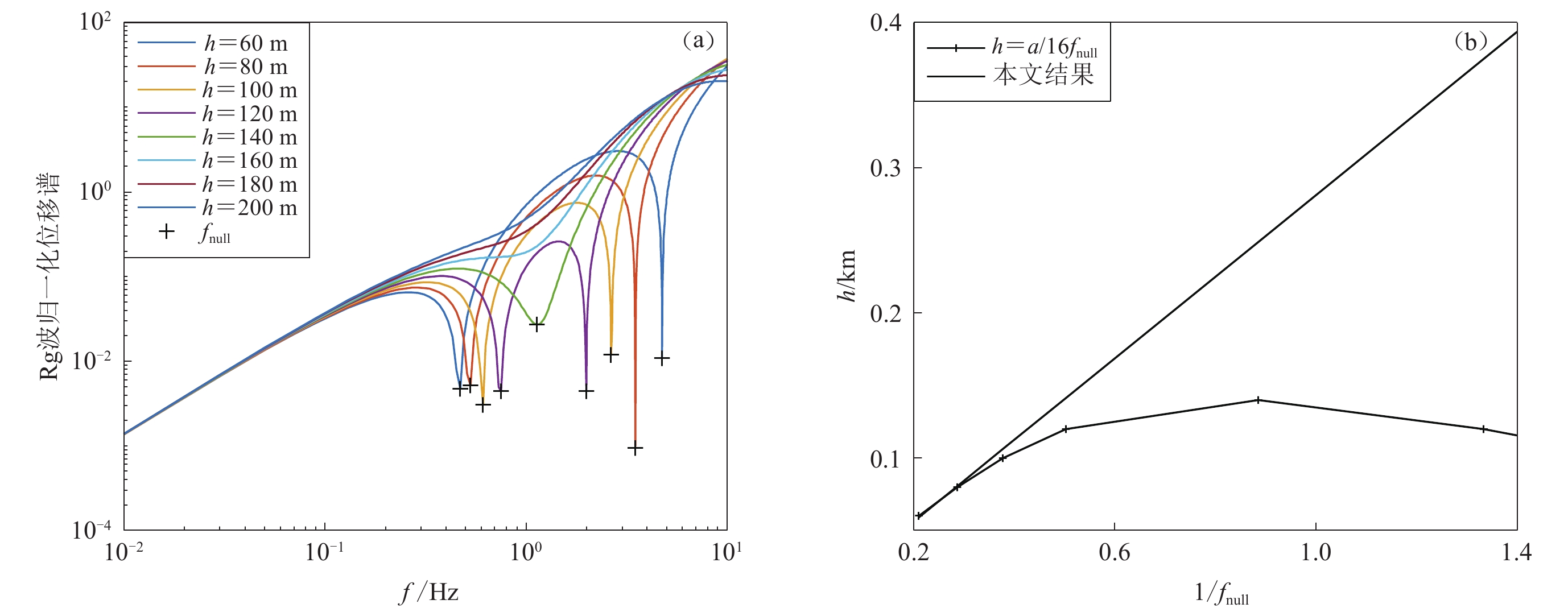
图 1 CLVD源埋深h为150 (a),200 (b),250 (c)和300 m (d)时不同相对强度下,ISO和CLVD源共同激发的Rg波归一化位移谱.ε为CLVD/ISO相对强度Figure 1. The normalized Rg spectra excited by conjunct sources of ISO and CLVD in different relative strengths at the CLVD source depths of 150 (a),200 (b),250 (c) and 300 m (d). ε is the relative strength of CLVD source to ISO source进一步分析给定CLVD源相对强度下,混合信号低谷点频率与CLVD源埋深的关系。考虑到地下爆炸中K指数通常为2 (Taylor,Patton,2013;Jin et al,2017),即CLVD/ISO相对强度为0.5,因此先计算该相对强度下不同CLVD源埋深时的Rg波位移谱,如图2a所示,图中一并给出了低谷点位置。可以看出,在CLVD源埋深较小时(小于140 m),混合信号位移谱中出现了两个低谷点,其中第一个低谷点频率与CLVD源埋深成正比,与式(4)的理论关系相反;当CLVD源埋深大于140 m时,低谷点已不明显直至消失。图2b给出了混合信号低谷点频率fnull与CLVD源埋深h的关系及与式(5)的比较,可以看出混合信号的fnull随h的增大先增大再减小,与理论式有很大差异,表明CLVD/ISO的相对强度为0.5时,CLVD源埋深较浅时混合信号会变得异常复杂。
![]() 图 2 低谷点频率与CLVD源埋深h的关系(a) CLVD/ISO相对强度为0.5时ISO和CLVD源共同激发的Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较Figure 2. The relationship between null frequency and the depth h of CLVD source(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.5; (b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)
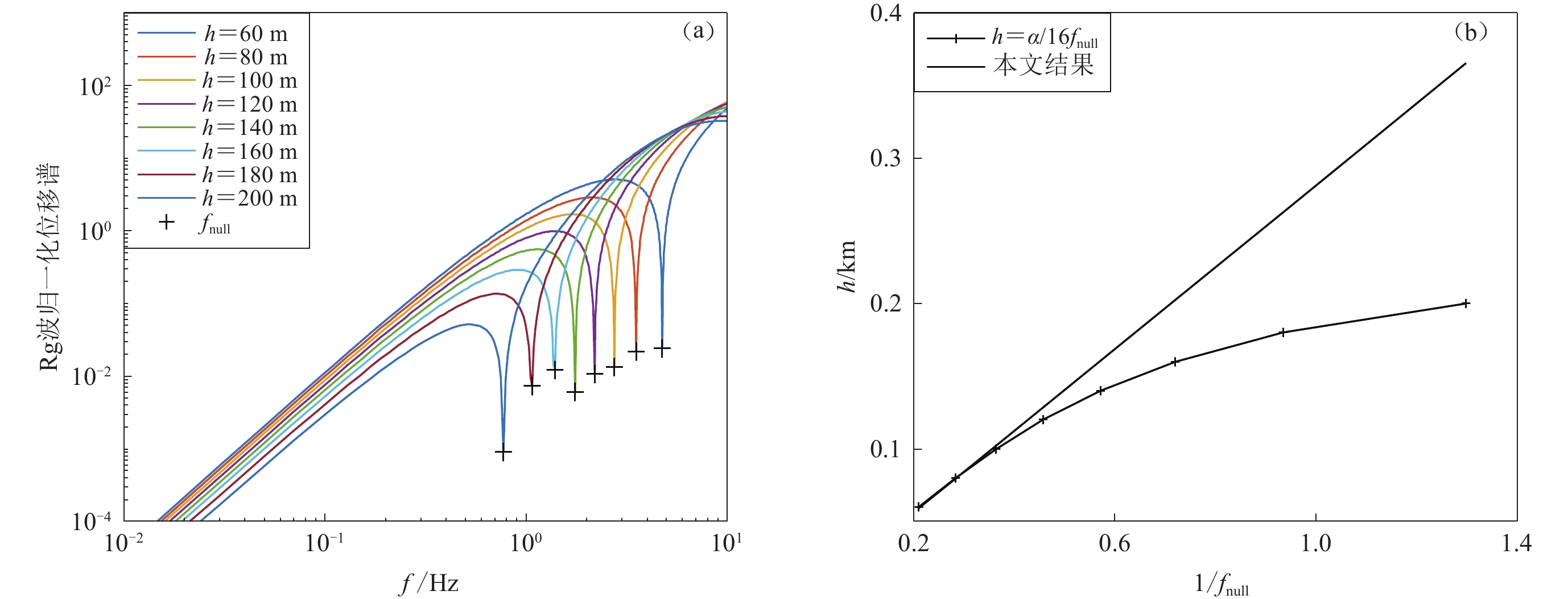
图 2 低谷点频率与CLVD源埋深h的关系(a) CLVD/ISO相对强度为0.5时ISO和CLVD源共同激发的Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较Figure 2. The relationship between null frequency and the depth h of CLVD source(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.5; (b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)CLVD/ISO相对强度为0.8时,不同CLVD源埋深下的Rg波位移谱如图3a所示,此时由于CLVD源相对强度较大,位移谱接近单一CLVD源作用的结果,即fnull随h的增大而减小。图3b定量给出了两者的比较,可以看出虽然混合信号的fnull与h成反比,但并非式(4)的线性关系,在CLVD源埋深较小时低谷点频率与理论预测一致,而埋深较大时则显著小于理论值。
![]() 图 3 低谷点频率与CLVD源埋深h的关系(a) CLVD/ISO相对强度为0.8时 ISO和CLVD 源共同激发的 Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较Figure 3. The relationship of null frequence to the depth h of CLVD source(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.8;(b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)
图 3 低谷点频率与CLVD源埋深h的关系(a) CLVD/ISO相对强度为0.8时 ISO和CLVD 源共同激发的 Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较Figure 3. The relationship of null frequence to the depth h of CLVD source(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.8;(b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)最后考虑两种震源源频谱差异对低谷点的影响,ISO源采用经典的MM71模型(Mueller,Murphy,1971),源频谱如式(8)所示,即
$$ S{\text{(}} \omega {\text{)}} {\text{=}} \frac{{{r_{\text{e}}}{P_{\text{p}}}\left( {{\text{i}}\omega {\text{+}} \dfrac{{P_0}}{{P_{\text{p}}}}{\omega _1}} \right)}}{{\rho {\text{(}} { - {\omega ^2} {\text{+}} 2{\text{i}}\omega {\omega _{\text{e}}}\dfrac\beta {\alpha } {\text{+}} \omega _{\text{e}}^2} {\text{)}}{\text{(}} {{\text{i}}\omega {\text{+}} {\omega _1}} {\text{)}}}} {\text{,}} $$ (8) 式中,re为弹性半径,Pp,P0分别为峰值压力和稳态压力,β和α分别为横波、纵波波速,ωe为源本征频率,ω1为衰减指数。
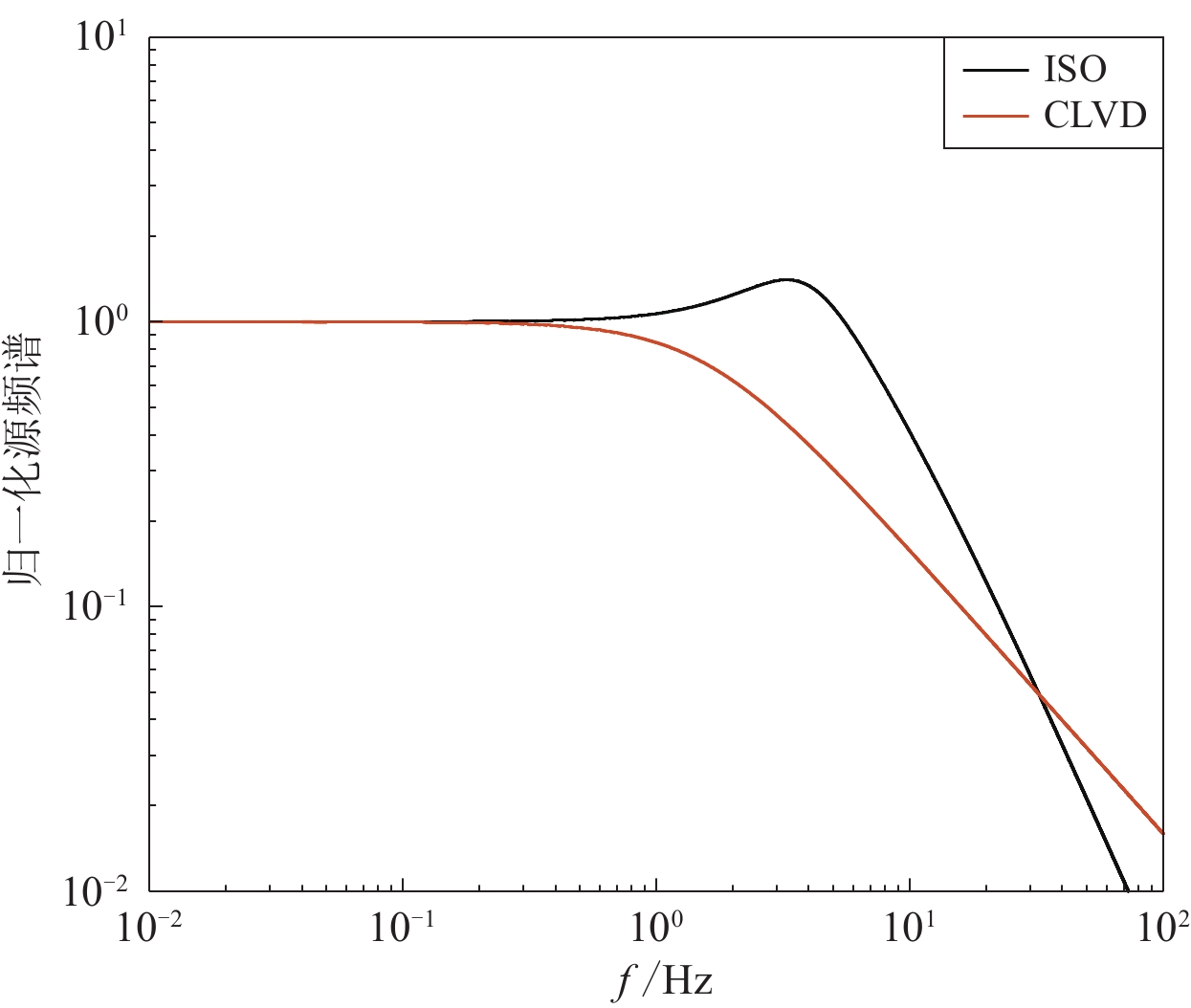
CLVD源时间函数采用Taylor和Patton (2013)给出的定义:S(t)=e−t/τ/τ,τ为特征时间常数。取α=4.5 km/s,β=2.6 km/s,ωe=8π,P0/Pp=0.3,ω1=20π,τ=0.1,两种源模型的比较如图4所示。可以看出,由于过冲的影响,在上文计算的低谷点频率(1 Hz)附近ISO源强度显著大于CLVD源。
引入源频谱后的Rg波位移谱如图5所示,其中CLVD源埋深从50 m开始。可以看出,h=50 m时(图5a),混合信号低谷点频率与单一CLVD源时的结果相当一致,并不随CLVD/ISO相对强度变化,h=100 m时的信号(图5b)似乎也有这样的特性,与图1中的结果呈现很大差别。同时相比于图1,在CLVD源埋深大于100 m时,低谷点已经不明显,即原先存在的低谷点已经消失(图5c,d)。
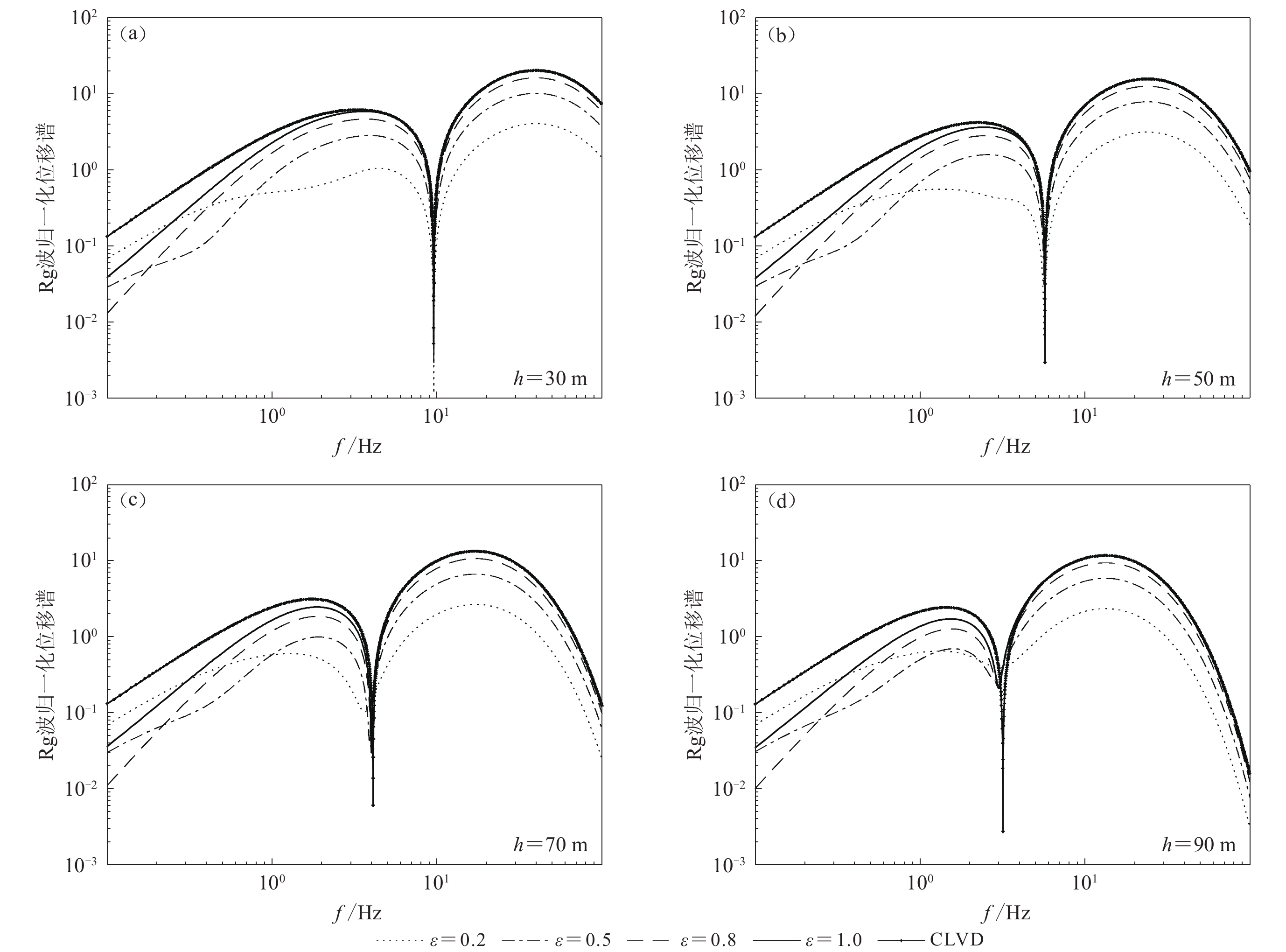
为探究这种现象是否普遍存在,我们计算了CLVD源埋深较浅时(30,50,70和90 m)的Rg波位移谱(图6)。可以看出,混合信号与图5a相同,出现了位置“稳定”的低谷点,其频率不随相对强度变化,表明此时CLVD源对低谷点起主导作用。
对于上述结果,可以进一步从理论上进行解释:根据式(2)和式(6),ISO和CLVD源激发的幅值中各自的位移本征函数r1相互抵消,因此会出现图1中混合信号幅值整体降低的现象;考虑源频谱差异时,图4表明在原先计算的低谷点频率附近ISO源频谱幅值更大,在计算混合信号位移谱时相当于增大了ISO源的相对强度,因此原先存在的低谷点会消失(图5);同时图4还表明ISO源在高频衰减相对更快,因此CLVD源埋深较浅时出现的频率较高的低谷点主要受CLVD源影响,其位置不再随CLVD/ISO相对强度变化(图6)。
3. 讨论与结论
本文研究了均匀半空间中,地下爆炸ISO源和CLVD源共同激发Rg波时,两种震源不同相对强度、埋深及源频谱对低谷点特性的影响。结果表明混合信号低谷点特性与单一CLVD源激发的信号有很大差异,CLVD/ISO源相对强度较小时低谷点不存在,低谷点存在时随CLVD源相对强度增大而增大,但小于单一CLVD源结果;CLVD源埋深较小时,低谷点频率与CLVD源埋深符合理论关系,埋深较大时低谷点频率则小于理论值;两种震源频谱的差异导致CLVD源埋深很小时混合信号才会出现低谷点,同时低谷点频率较高并不再随CLVD/ISO相对强度变化。综上所述,实际地下爆炸中,ISO源与CLVD源共同作用激发的Rg波信号低谷点频率与CLVD源埋深不符合理论的线性反比关系,因此不能直接利用理论式估算CLVD源埋深进而估算爆炸埋深。
根据本文研究结果,不考虑源频谱影响的情况下,当观测到的地下爆炸Rg波信号存在明显的低谷点时,表明CLVD/ISO相对强度较大(大于0.5)。此时混合信号受两种震源的共同作用,相比于单一CLVD源的情况,低谷点频率变小,则根据理论反比关系推算的CLVD源埋深会变大,进而导致估算的地下爆炸埋深偏大。
本文从震源角度分析了Rg波低谷点特性,在计算混合信号归一化位移谱时去除了格林函数的影响,而Baker等(2012a)和徐恒垒等(2011)的结果分别表明,介质的速度结构及地表起伏对低谷点的产生及位置都有一定影响。因此综合来看,Rg波低谷点同时受震源特性和介质模型两方面的影响,在利用低谷点频率估算地下爆炸埋深时,需要同时考虑这两种因素。
-
图 1 CLVD源埋深h为150 (a),200 (b),250 (c)和300 m (d)时不同相对强度下,ISO和CLVD源共同激发的Rg波归一化位移谱.ε为CLVD/ISO相对强度
Figure 1. The normalized Rg spectra excited by conjunct sources of ISO and CLVD in different relative strengths at the CLVD source depths of 150 (a),200 (b),250 (c) and 300 m (d). ε is the relative strength of CLVD source to ISO source
图 2 低谷点频率与CLVD源埋深h的关系
(a) CLVD/ISO相对强度为0.5时ISO和CLVD源共同激发的Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较
Figure 2. The relationship between null frequency and the depth h of CLVD source
(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.5; (b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)
图 3 低谷点频率与CLVD源埋深h的关系
(a) CLVD/ISO相对强度为0.8时 ISO和CLVD 源共同激发的 Rg波归一化位移谱;(b) fnull随h变化与理论式h=α/(16fnull)的比较
Figure 3. The relationship of null frequence to the depth h of CLVD source
(a) The normalized Rg spectra excited by conjunct sources of ISO and CLVD with the relative strength of CLVD/ISO 0.8;(b) Comparison between the relationship of fnull to h and the theoretical formula h=α/(16fnull)
-
何永锋,陈晓非,何耀峰,靳平. 2005. 地下爆炸Rg波低谷点激发机理[J]. 地球物理学报,48(3):643–648. doi: 10.3321/j.issn:0001-5733.2005.03.023 He Y F,Chen X F,He Y F,Jin P. 2005. Generation of null in Rg wave by underground explosions[J]. Chinese Journal of Geophysics,48(3):643–648 (in Chinese). doi: 10.1002/cjg2.697
徐恒垒,靳平,倪四道,刘文学,王红春,李欣. 2011. 谱元法数值模拟地表起伏对补偿线性矢量偶极源Rg波低谷点的影响[J]. 地球物理学报,54(11):2831–2837. doi: 10.3969/j.issn.0001-5733.2011.11.013 Xu H L,Jin P,Ni S D,Liu W X,Wang H C,Li X. 2011. Investigation of surface fluctuation effects on the spectral null of Rg waves generated by CLVD source with spectral element method simulation[J]. Chinese Journal of Geophysics,54(11):2831–2837 (in Chinese).
Aki K, Richards P G. 1980. Quantitative Seismology[M]. San Francisco: W. H. Freeman: 319–322.
Baker G E,Stevens J L,Xu H M. 2012a. Explosion shear-wave generation in high-velocity source media[J]. Bull Seismol Soc Am,102(4):1301–1319. doi: 10.1785/0120110119
Baker G E,Stevens J L,Xu H M. 2012b. Explosion shear-wave generation in low-velocity source media[J]. Bull Seismol Soc Am,102(4):1320–1334. doi: 10.1785/0120110165
Denny M D,Johnson L R. 1991. The explosion seismic source function:Models and scaling laws reviewed[J]. Explo Source Phenomenol,65:1–24.
Gupta I N,Chan W W,Wagner R A. 1992. A comparison of regional phases from underground nuclear explosions at east kazakh and nevada test sites[J]. Bull Seismol Soc Am,82(1):352–382.
Gupta I N,Zhang T R,Wagner R A. 1997. Low-frequency Lg from NTS and kazakh nuclear explosions:Observations and interpretation[J]. Bull Seismol Soc Am,87(5):1115–1125.
Jin P,Xu H L,Wang H C,Pan C Z,Xu X,Wang X L. 2017. Secondary seismic sources behind amplitude ratios between the first 2016 and 2013 North Korean nuclear tests[J]. Geophys J Int,211(1):322–334. doi: 10.1093/gji/ggx289
Massé R P. 1981. Review of seismic source models for underground nuclear explosions[J]. Bull Seismol Soc Am,71(4):1249–1268. doi: 10.1785/BSSA0710041249
Mueller R A,Murphy J R. 1971. Seismic characteristics of underground nuclear detonations:Part I. Seismic spectrum scaling[J]. Bull Seismol Soc Am,61(6):1675–1692. doi: 10.1785/BSSA0610061675
Patton H J,Taylor S R. 1995. Analysis of Lg spectral ratios from NTS explosions:Implications for the source mechanisms of spall and the generation of Lg waves[J]. Bull Seismol Soc Am,85(1):220–236.
Patton H J,Taylor S R. 2011. The apparent explosion moment:Inferences of volumetric moment due to source medium damage by underground nuclear explosions[J]. J Geophys Res,116(B3):B03310.
Taylor S R, Patton H J. 2013. Can teleseismic mb be affected by rock damage around explosions?[J] Geophys Res Lett, 40(1): 100–104.




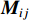
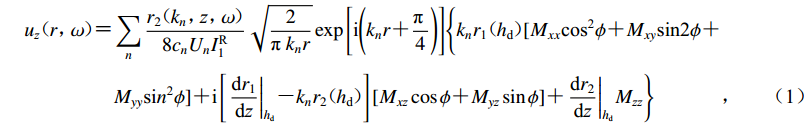
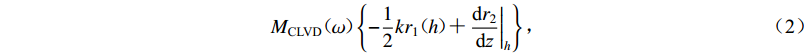
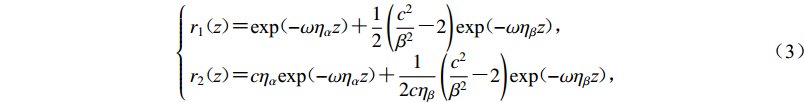


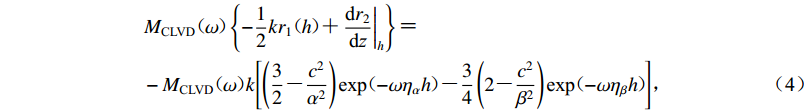
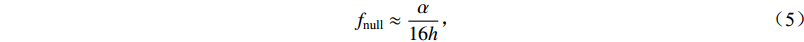
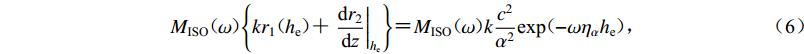
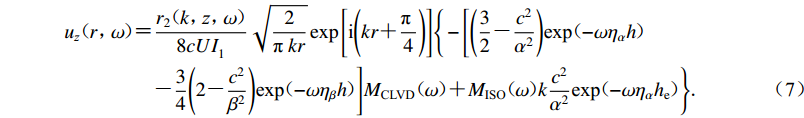
 下载:
下载: