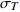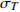高级搜索

俯冲带板内地震竖向加速度谱阻尼修正系数模型研究

陈心锋, 姜妍旭, 刘名吉

陈心锋，姜妍旭，刘名吉. 2022. 俯冲带板内地震竖向加速度谱阻尼修正系数模型研究. 地震学报，44（2）：339−355. DOI: 10.11939/jass.20200198
引用本文: 陈心锋，姜妍旭，刘名吉. 2022. 俯冲带板内地震竖向加速度谱阻尼修正系数模型研究. 地震学报，44（2）：339−355. DOI: 10.11939/jass.20200198
shu
Chen X F，Jiang Y X，Liu M J. 2022. A damping modification factor model for vertical acceleration spectrum from slab earthquakes in subduction zone. Acta Seismologica Sinica，44（2）：339−355. DOI: 10.11939/jass.20200198
Citation: Chen X F，Jiang Y X，Liu M J. 2022. A damping modification factor model for vertical acceleration spectrum from slab earthquakes in subduction zone. Acta Seismologica Sinica，44（2）：339−355. DOI: 10.11939/jass.20200198
shu

俯冲带板内地震竖向加速度谱阻尼修正系数模型研究

  • 中国济南 250000 山东建筑大学土木工程学院

基金项目: 国家自然科学基金（51878396）资助
详细信息
    通讯作者:

    陈心锋，硕士研究生，主要从事岩土地震工程方面的研究，e-mail：chenxf1996@126.com

  • 中图分类号: P315.9

A damping modification factor model for vertical acceleration spectrum from slab earthquakes in subduction zone

  • School of Civil Engineering，Shandong Jianzhu University，Ji’nan 250000，China

摘要

    摘要
  • 摘要: 基于日本K-NET和KiK-net台网的4 695条俯冲带板内地震记录，采用最小二乘法对阻尼修正系数（DMF）的几何均值进行关于阻尼比和谱周期的回归拟合，分场地类别建立了考虑阻尼比和谱周期的竖向加速度谱DMF模型。为探究震源、路径和场地效应对该模型残差分布的影响，采用随机效应模型将残差分离得到各类残差及相应的残差标准差，在此基础上进行DMF模型残差分析。研究结果表明，DMF可以采用阻尼比对数值的三次多项式、周期对数值的四次多项式来模拟。由于规范设计反应谱并非针对某一特定地震，规范提出的DMF模型并不包含震源和路径参数，但事件间和事件内残差关于矩震级、断层距离和断层深度的分布表明，在给定地震事件下，包含地震动参数的DMF模型将会改善模型的预测能力。
    Abstract: In this study, 4695 strong-motion records from subduction slab earthquakes in Japan obtained by the K-NET and KiK-net networks were used to develop a damping modification factor （DMF） model for the vertical acceleration spectrum. The DMF model considering the damping ratio and spectral period is established for four site classes, and the geometric mean values for DMF are used to perform regression fitting in respect to the damping ratio and spectral period by least squares method. To evaluate the influence of hypocenter, path, and site effects on the residual distribution of the model, the total model residuals and standard deviations were separated into between-event and within-event parts, and the within-event residuals were further divided into the between-site and within-site parts by using a random effects model. The results show that the effect of damping ratios on DMF can be modelled by the third-order polynomial of the logarithm of the damping ratios, a fourth-order polynomial of the logarithm of spectral periods can be used to model the effect of spectral periods for the DMF. The effects of source and path parameters were not modelled in this study because of DMF model is used to scale a design spectrum not associated with a given scenario earthquake. The distribution of the between- and within-event residual distributions with respect to moment magnitude, fault depth and source distance suggests that including these terms would improve prediction capability of the model when a DMF is designed for scaling a 5% acceleration spectrum associated with a scenario event for a give magnitude and source distance.
    • HTML全文

  • 图  1   地震数据分布图

    （a） 地震记录关于矩震级和断层距离的分布；（b） 地震事件关于矩震级和断层深度的分布

    Figure  1.   The distribution of earthquake dataset （a） The distribution of earthquake records with respect to moment magnitude and source distance；（b） The distribution of earthquakes with respect to moment magnitude and fault depth

    下载: 全尺寸图片 幻灯片

    图  2   四类场地阻尼修正系数DMF的几何均值分布情况

    Figure  2.   The geometric mean values of DMF for four site classes

    （a） ζ＝1%；（b） ζ＝3%；（c） ζ＝15% ；（d） ζ＝30%

    下载: 全尺寸图片 幻灯片

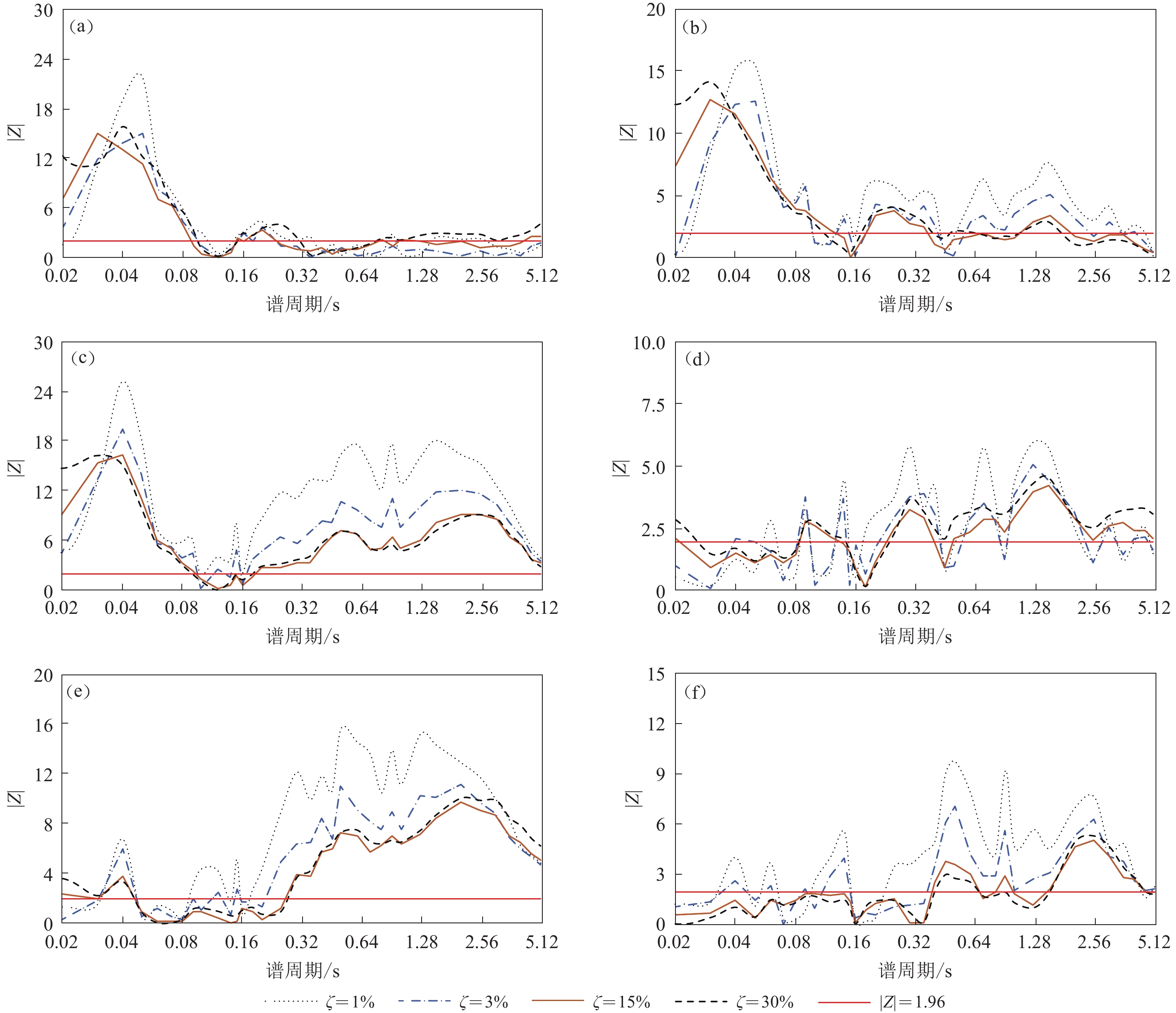
    图  3   四类场地间显著性检验统计值|Z|

    （a） Ⅰ类场地与Ⅱ类场地；（b） Ⅰ类场地与Ⅲ类场地；（c） Ⅰ类场地与Ⅳ类场地；（d） Ⅱ类场地与Ⅲ类场地；（e） Ⅱ类场地与Ⅳ类场地；（f） Ⅲ类场地与Ⅳ类场地

    Figure  3.   |Z| values for the statistical tests between each pair of four site classes

    （a） Site class Ⅰ vs site class Ⅱ；（b） Site class Ⅰ vs site class Ⅲ；（c） Site class Ⅰ vs site class Ⅳ； （d） Site class Ⅱ vs site class Ⅲ；（e） Site class Ⅱ vs site class Ⅳ；（f） Site class Ⅲ vs site class Ⅳ

    下载: 全尺寸图片 幻灯片

    图  4   四类场地不同阻尼比的阻尼修正系数DMF模型拟合曲线与数据几何均值的对比

    （a） Ⅰ类场地；（b） Ⅱ类场地；（c） Ⅲ类场地；（d） Ⅳ类场地

    Figure  4.   DMF model comparisons with the geometrical mean of the vertical components for eight damping ratios of four site classes

    （a） Site class Ⅰ；（b） Site class Ⅱ；（c） Site class Ⅲ；（d） Site class Ⅳ

    下载: 全尺寸图片 幻灯片

    图  5   阻尼修正系数DMF模型的残差标准差关于谱周期的分布图

    Figure  5.   The distribution of standard deviations of DMF models

    （a） ζ＝1%；（b） ζ＝3%；（c） ζ＝10%；（d） ζ＝30%

    下载: 全尺寸图片 幻灯片

    图  6   阻尼比为25%时四类场地的场地内标准差（a）和场地间标准差（b）分布图

    Figure  6.   Distribution of within-site （a） and between-site （b） standard deviation for four site classes for a damping ratio of 25%

    下载: 全尺寸图片 幻灯片

    图  7   T＝2.5 s时阻尼修正系数DMF模型标准差关于对数坐标系下阻尼比的变化图

    （a） Ⅰ类场地；（b） Ⅱ类场地；（c） Ⅲ类场地；（d） Ⅳ类场地

    Figure  7.   Variations of standard deviation of DMF model with damping ratio at logarithmic scale by T＝2.5 s

    （a） Site class Ⅰ；（b） Site class Ⅱ；（c） Site class Ⅲ；（d） Site class Ⅳ

    下载: 全尺寸图片 幻灯片

    图  8   阻尼比为25%时阻尼修正系数DMF模型事件间残差分布图

    （a） T＝0.1 s时残差关于断层深度的分布图；（b） T＝0.1 s时残差关于矩震级的分布图；（c） T＝3.0 s时残差关于断层深度的分布图；（d） T＝3.0 s时残差关于矩震级的分布图

    Figure  8.   The distributions of between-event residuals of DMF model for a damping ratio of 25%

    （a） The distribution of residuals with respect to fault depth at T＝0.1 s；（b） The distribution of residuals with respect to moment magnitude at T＝0.1 s；（c） The distribution of residuals with respect to fault depth at T＝3.0 s；（d） The distribution of residuals with respect to moment magnitude at T＝3.0 s

    下载: 全尺寸图片 幻灯片

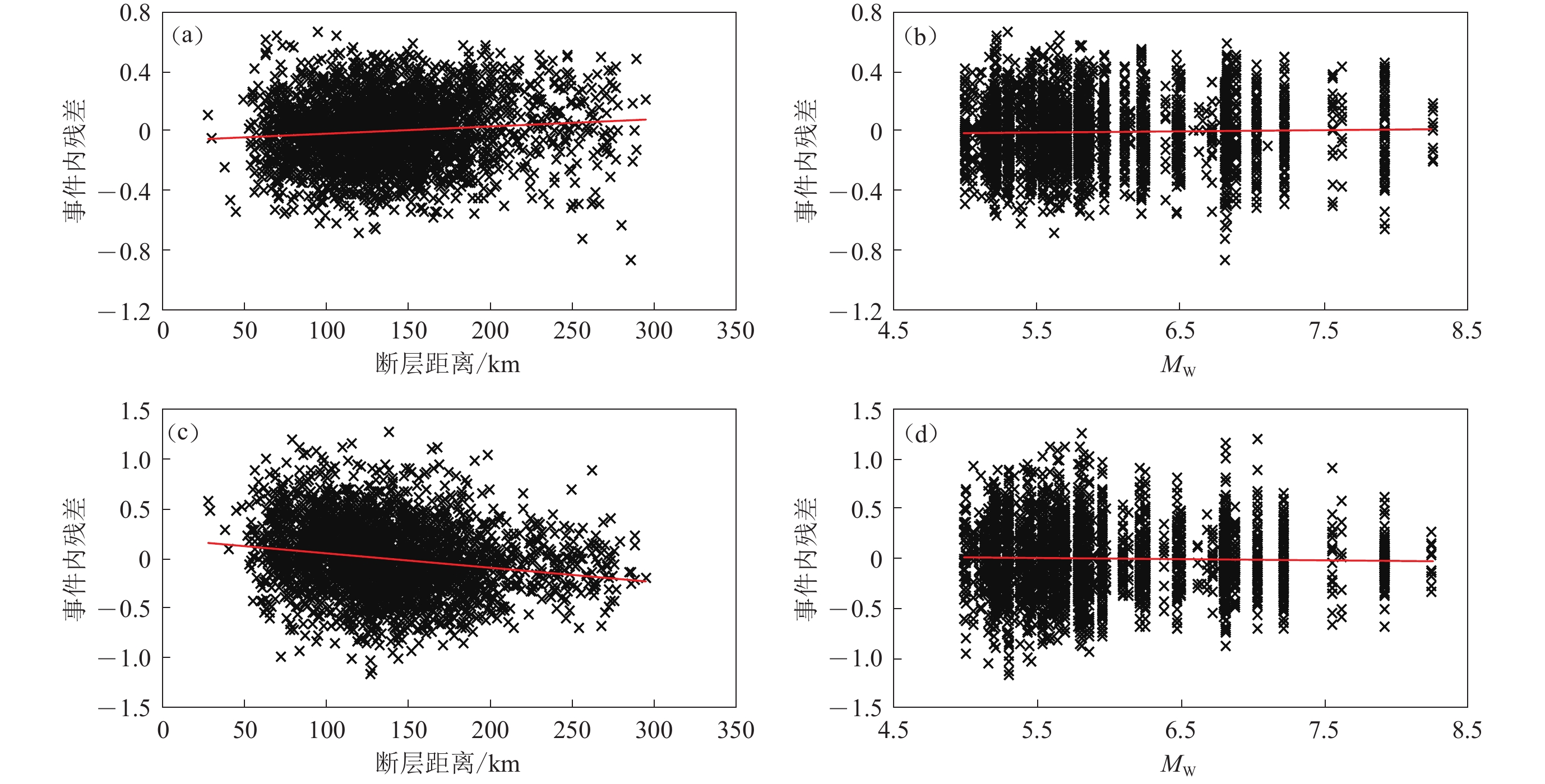
    图  9   阻尼比为25%时DMF模型事件内残差分布图

    （a） T＝0.1 s时残差关于断层距离的分布图；（b） T＝0.1 s时残差关于矩震级的分布图；（c） T＝3.0 s时残差关于断层距离的分布图；（d） T＝3.0 s时残差关于矩震级的分布图

    Figure  9.   The distributions of within-event residuals of DMF model for a damping ratio of 25%

    （a） The distribution of residuals with respect to fault distance at T＝0.1 s；（b） The distribution of residuals with respect to moment magnitude at T＝0.1 s；（c） The distribution of residuals with respect to fault distance at T＝3.0 s；（d） The distribution of residuals with respect to moment magnitude at T＝3.0 s

    下载: 全尺寸图片 幻灯片

    表  1   场地类别定义和各类场地记录数量

    Table  1   Site class definition and number of the records in each site class

    场地类别土质类型场地周期/s记录条数
    Ⅰ岩石Ts＜0.22 022
    Ⅱ硬土0.2≤Ts＜0.41 353
    Ⅲ中硬土0.4≤Ts＜0.6442
    Ⅳ软土Ts≥0.6878
    下载: 导出CSV

    表  2   四类场地下阻尼修正系数模型的系数值

    Table  2   Coefficients of DMF model for four site classes

    T/sⅠ类场地Ⅱ类场地Ⅲ类场地Ⅳ类场地
    $ {c}_{1} $$ {c}_{2} $$ {c}_{3} $$ {c}_{1} $$ {c}_{2} $$ {c}_{3} $$ {c}_{1} $$ {c}_{2} $$ {c}_{3} $$ {c}_{1} $$ {c}_{2} $$ {c}_{3} $
    0.03 −0.020 0 −0.011 3 −0.015 0 −0.020 0 −0.005 4 −0.008 0 −0.008 3 −0.004 8 −0.008 0 −0.007 1 −0.004 7 −0.010 0
    0.04 −0.234 3 0.012 9 0.001 0 −0.152 1 0.016 7 −0.005 0 −0.138 9 0.018 3 −0.004 0 −0.120 8 0.013 3 −0.004 0
    0.05 −0.294 9 0.005 7 0.000 1 −0.235 9 0.012 9 0.001 4 −0.213 8 0.012 3 −0.001 1 −0.220 4 0.013 0 0.002 4
    0.06 −0.322 8 0.001 8 0.002 6 −0.283 5 0.006 7 0.003 1 −0.262 1 0.009 1 0.001 9 −0.273 8 0.008 2 0.005 0
    0.07 −0.340 8 −0.001 1 0.004 4 −0.314 7 0.002 1 0.004 4 −0.294 4 0.006 1 0.003 8 −0.308 7 0.004 7 0.006 6
    0.08 −0.352 8 −0.003 2 0.005 9 −0.335 7 −0.001 4 0.005 4 −0.317 1 0.003 4 0.005 1 −0.332 4 0.002 0 0.007 7
    0.09 −0.361 1 −0.004 9 0.007 1 −0.350 3 −0.004 0 0.006 2 −0.333 4 0.001 0 0.006 1 −0.349 1 −0.000 1 0.008 5
    0.10 −0.366 8 −0.006 3 0.008 1 −0.360 5 −0.006 1 0.007 0 −0.345 4 −0.001 0 0.006 8 −0.361 1 −0.001 8 0.009 1
    0.12 −0.373 5 −0.008 2 0.009 7 −0.372 8 −0.008 9 0.008 2 −0.361 2 −0.004 4 0.007 9 −0.376 3 −0.004 3 0.009 9
    0.14 −0.376 5 −0.009 4 0.011 0 −0.378 8 −0.010 6 0.009 3 −0.370 3 −0.007 0 0.008 7 −0.384 6 −0.006 1 0.010 5
    0.15 −0.377 1 −0.009 8 0.011 5 −0.380 3 −0.011 2 0.009 9 −0.373 4 −0.008 1 0.009 0 −0.387 3 −0.006 7 0.010 8
    0.16 −0.377 4 −0.010 1 0.012 1 −0.381 2 −0.011 6 0.010 4 −0.375 7 −0.009 0 0.009 3 −0.389 3 −0.007 3 0.011 0
    0.18 −0.377 1 −0.010 5 0.013 0 −0.381 6 −0.012 0 0.011 3 −0.378 8 −0.010 5 0.009 9 −0.391 8 −0.008 2 0.011 4
    0.20 −0.376 2 −0.010 7 0.013 9 −0.380 8 −0.012 1 0.012 2 −0.380 4 −0.011 6 0.010 5 −0.393 1 −0.008 8 0.011 8
    0.25 −0.372 3 −0.010 4 0.015 7 −0.376 3 −0.011 3 0.014 2 −0.381 1 −0.013 1 0.011 8 −0.393 4 −0.009 6 0.012 9
    0.30 −0.367 6 −0.009 5 0.017 2 −0.370 3 −0.009 7 0.016 0 −0.379 3 −0.013 5 0.013 1 −0.392 2 −0.009 7 0.013 9
    0.35 −0.362 7 −0.008 3 0.018 6 −0.364 2 −0.007 7 0.017 6 −0.376 6 −0.013 1 0.014 4 −0.390 6 −0.009 5 0.014 9
    0.40 −0.357 9 −0.006 9 0.019 8 −0.358 2 −0.005 5 0.019 2 −0.373 5 −0.012 2 0.015 6 −0.388 9 −0.008 9 0.016 0
    0.45 −0.353 2 −0.005 4 0.020 8 −0.352 5 −0.003 1 0.020 5 −0.370 1 −0.011 0 0.016 8 −0.387 3 −0.008 2 0.017 0
    0.50 −0.348 6 −0.003 8 0.021 8 −0.347 1 −0.000 8 0.021 8 −0.366 7 −0.009 5 0.018 0 −0.385 7 −0.007 3 0.018 0
    0.60 −0.339 8 −0.000 5 0.023 6 −0.337 0 0.003 9 0.024 1 −0.359 9 −0.006 2 0.020 2 −0.382 5 −0.005 4 0.020 0
    0.70 −0.331 3 0.002 9 0.025 0 −0.327 7 0.008 4 0.026 0 −0.353 1 −0.002 6 0.022 2 −0.379 3 −0.003 1 0.021 8
    0.80 −0.323 0 0.006 2 0.026 3 −0.319 0 0.012 8 0.027 7 −0.346 2 0.001 1 0.024 1 −0.375 9 −0.000 8 0.023 5
    0.90 −0.314 9 0.009 4 0.027 5 −0.310 6 0.016 9 0.029 2 −0.339 2 0.004 8 0.025 8 −0.372 2 0.001 6 0.025 1
    1.00 −0.306 8 0.012 6 0.028 5 −0.302 4 0.020 9 0.030 5 −0.332 2 0.008 5 0.027 3 −0.368 1 0.004 1 0.026 6
    1.25 −0.286 8 0.020 2 0.030 6 −0.282 5 0.030 0 0.033 1 −0.314 2 0.017 4 0.030 5 −0.356 2 0.010 4 0.029 8
    1.50 −0.266 7 0.027 4 0.032 1 −0.262 7 0.038 1 0.034 9 −0.295 4 0.025 6 0.033 1 −0.342 1 0.016 7 0.032 4
    2.00 −0.226 4 0.040 4 0.034 2 −0.222 5 0.052 1 0.037 2 −0.256 0 0.040 4 0.036 5 −0.307 9 0.029 0 0.036 2
    2.50 −0.185 6 0.052 2 0.035 3 −0.181 3 0.063 7 0.038 1 −0.214 6 0.053 0 0.038 4 −0.267 9 0.040 9 0.038 7
    3.00 −0.144 7 0.062 9 0.035 8 −0.139 1 0.073 8 0.038 1 −0.171 9 0.064 0 0.039 1 −0.223 6 0.052 3 0.040 3
    3.50 −0.103 8 0.072 8 0.035 9 −0.096 2 0.082 6 0.037 6 −0.128 3 0.073 7 0.039 1 −0.176 3 0.063 2 0.041 1
    4.00 −0.063 1 0.082 0 0.035 6 −0.052 9 0.090 4 0.036 6 −0.084 1 0.082 2 0.038 4 −0.126 9 0.073 8 0.041 3
    4.50 −0.022 6 0.090 6 0.035 1 −0.009 2 0.097 4 0.035 2 −0.039 6 0.089 8 0.037 3 −0.075 9 0.084 0 0.041 1
    5.00 0.017 7 0.098 7 0.034 4 0.034 6 0.103 8 0.033 6 0.005 0 0.096 7 0.035 8 −0.023 8 0.093 9 0.040 6
    下载: 导出CSV

    表  3   阻尼修正系数模型的总残差标准差${\sigma _T} $

    Table  3   Total standard deviations ${\sigma _T} $ of DMF model

    T/sσT
    ζ＝1%ζ＝2%ζ＝3%ζ＝4%ζ＝6%ζ＝7%ζ＝8%ζ＝9%ζ＝10%ζ＝15%ζ＝20%ζ＝25%ζ＝30%
    0.030.056 00.014 70.011 60.005 70.000 00.005 40.010 40.015 20.019 80.024 30.046 00.066 50.086 4
    0.040.242 60.146 30.084 40.039 90.030 80.055 70.079 90.094 80.110 70.167 60.204 10.229 50.248 6
    0.050.238 60.148 70.087 90.042 50.033 00.060 10.082 90.102 70.120 20.184 10.225 50.255 40.277 7
    0.060.225 00.144 40.092 90.042 70.035 80.061 40.090 20.105 60.123 70.190 90.235 10.267 00.290 8
    0.070.215 50.139 60.090 00.041 50.034 60.059 80.088 00.103 00.120 70.187 60.232 00.263 60.287 1
    0.080.206 30.141 40.085 50.039 80.033 20.057 50.084 00.099 00.115 90.178 70.220 10.250 30.273 1
    0.090.200 40.136 40.082 70.038 50.030 80.056 20.082 30.096 20.112 70.174 60.215 70.245 10.266 9
    0.100.192 70.132 40.080 70.037 30.029 50.053 70.078 70.097 70.107 80.165 90.205 10.233 30.254 2
    0.120.188 50.122 90.077 80.034 50.030 50.055 60.076 60.094 80.105 70.160 90.197 30.223 80.243 6
    0.140.189 90.123 00.077 20.035 70.029 70.053 70.073 40.090 30.104 60.157 00.184 40.208 30.227 0
    0.150.188 80.122 10.076 80.033 10.029 40.053 40.069 30.090 80.105 90.159 40.194 30.208 60.227 8
    0.160.190 80.122 60.077 60.033 90.030 10.054 40.074 80.092 20.107 10.161 30.196 20.210 30.230 1
    0.180.191 80.123 90.074 00.035 20.029 00.052 60.072 00.088 50.102 90.155 70.190 80.207 50.228 1
    0.200.191 20.123 50.076 80.035 70.029 70.053 90.070 90.090 90.105 60.159 20.194 60.212 30.233 3
    0.250.191 70.124 30.077 00.035 50.029 50.053 30.069 80.085 90.104 50.150 00.184 40.211 70.235 5
    0.300.195 60.125 80.075 40.035 90.029 80.053 50.073 10.089 70.104 20.152 30.189 10.219 40.246 6
    0.350.191 20.129 80.077 50.034 00.029 50.053 40.070 00.090 90.106 40.163 80.195 20.227 40.256 7
    0.400.195 00.131 80.078 40.033 90.030 10.051 60.070 90.093 20.108 90.159 60.201 90.238 10.270 9
    0.450.198 70.128 20.077 90.035 80.029 80.054 40.072 80.089 90.108 60.163 80.208 50.247 50.283 4
    0.500.200 20.127 60.079 80.036 70.030 70.056 00.077 10.095 40.111 50.168 60.216 10.257 70.296 3
    0.600.199 60.128 40.077 50.037 70.030 10.054 90.076 10.097 80.111 40.177 90.231 70.278 70.321 8
    0.700.204 60.131 80.083 30.036 70.032 30.056 40.081 90.097 90.115 50.187 30.246 80.299 60.347 5
    0.800.208 80.133 90.084 60.037 00.033 20.058 00.084 90.100 90.119 30.196 40.260 30.316 30.367 4
    0.900.207 70.132 60.085 00.036 90.033 40.057 80.086 00.102 10.121 30.202 30.270 00.329 00.382 3
    1.000.211 50.134 70.086 10.039 80.031 80.058 90.083 20.104 90.125 00.210 30.281 60.343 50.398 6
    1.250.212 40.139 30.084 30.041 00.033 80.063 00.088 80.112 60.134 90.230 70.309 60.377 60.436 5
    1.500.216 50.143 50.087 80.041 00.036 10.067 90.096 30.122 60.147 10.252 20.340 20.413 00.475 9
    2.000.226 10.153 80.095 20.045 10.040 40.076 70.109 00.139 10.167 80.290 50.389 20.470 30.536 1
    2.500.231 10.160 70.100 60.048 00.043 90.083 50.119 70.153 30.185 10.321 30.426 20.510 20.576 5
    3.000.237 00.166 70.105 60.050 80.046 70.089 10.128 20.164 50.198 30.341 70.450 80.533 90.598 3
    3.500.245 70.175 60.112 10.054 30.050 20.096 00.137 50.176 20.212 80.363 00.473 30.556 30.619 1
    4.000.248 40.179 30.115 30.055 50.051 50.098 90.142 60.183 20.220 50.372 70.481 90.561 40.621 2
    4.500.258 30.187 30.120 40.058 40.054 00.103 50.149 10.191 10.229 90.385 10.495 00.573 20.630 5
    5.000.264 90.194 20.126 40.061 30.056 70.108 00.154 90.197 50.237 10.391 70.498 40.573 20.627 1
    下载: 导出CSV

    表  4   阻尼修正系数模型的事件内残差标准差σ

    Table  4   Within-event standard deviation σ of DMF model

    T/sσ
    ζ＝1%ζ＝2%ζ＝3%ζ＝4%ζ＝6%ζ＝7%ζ＝8%ζ＝9%ζ＝10%ζ＝15%ζ＝20%ζ＝25%ζ＝30%
    0.030.017 80.013 80.009 70.005 10.000 00.004 90.009 40.013 70.017 60.021 30.037 90.051 10.061 9
    0.040.221 00.134 70.078 60.035 30.028 80.051 80.071 20.088 00.102 60.154 90.188 30.211 50.228 8
    0.050.222 30.140 00.083 10.037 90.031 00.056 30.077 60.096 10.112 20.171 20.209 10.236 10.256 0
    0.060.213 50.137 80.083 20.038 40.032 30.058 50.080 80.100 10.117 00.178 80.218 80.247 10.268 1
    0.070.206 40.134 00.081 10.037 40.031 20.057 00.078 60.097 30.113 70.174 80.214 50.242 40.263 1
    0.080.199 10.129 50.078 40.036 40.030 40.055 00.075 80.093 80.109 30.165 90.202 60.229 20.249 4
    0.090.195 30.126 80.076 60.035 50.029 90.054 40.074 80.092 40.107 60.163 70.200 80.227 10.246 8
    0.100.186 10.121 20.073 60.034 10.028 50.051 80.071 40.088 40.103 10.157 00.193 10.218 90.238 2
    0.120.183 30.119 80.072 40.033 50.028 20.051 30.070 70.087 40.101 80.154 20.188 50.213 60.232 3
    0.140.182 70.119 00.071 60.033 20.027 60.050 00.068 70.084 60.098 20.147 60.179 50.202 20.219 6
    0.150.181 40.117 50.070 30.032 20.027 00.049 10.067 50.083 20.097 00.146 60.178 90.202 10.220 1
    0.160.184 50.118 70.071 90.033 20.027 60.050 00.068 80.084 80.098 50.148 40.180 60.204 10.222 8
    0.180.185 30.120 00.072 30.033 10.027 30.049 40.067 50.082 70.096 10.144 70.177 10.201 10.220 6
    0.200.184 50.119 50.071 50.033 20.027 8−0.050 50.069 20.085 10.098 80.148 50.181 40.206 00.225 5
    0.250.184 00.118 80.071 40.032 90.027 30.049 30.067 80.083 40.096 90.144 50.176 50.201 10.221 7
    0.300.188 10.120 80.072 90.033 50.027 9−0.050 20.068 80.084 70.098 30.147 60.181 70.208 70.231 9
    0.350.185 60.119 70.072 10.033 30.027 70.050 10.068 70.085 00.099 20.151 90.188 50.217 70.242 9
    0.400.188 70.120 70.072 30.033 20.027 9−0.050 60.069 50.085 80.100 10.154 80.194 00.226 40.254 2
    0.450.192 20.123 60.073 60.033 70.028 30.051 40.070 80.087 30.101 80.156 90.197 70.231 80.261 7
    0.500.193 40.123 40.074 50.034 30.028 60.052 20.071 90.088 80.103 60.160 30.202 00.237 10.268 4
    0.600.191 40.122 70.074 20.034 30.029 00.052 80.072 90.090 40.105 90.165 70.211 60.250 00.283 3
    0.700.195 40.125 90.075 50.035 10.029 50.053 80.074 50.092 40.108 50.171 50.220 60.262 20.297 4
    0.800.199 80.128 10.076 80.035 50.030 10.054 70.075 60.093 80.110 20.176 30.228 30.271 80.308 7
    0.900.198 20.127 10.076 40.035 40.029 90.054 90.076 50.095 70.113 00.182 00.236 10.280 80.318 7
    1.000.199 60.127 00.075 80.035 00.029 70.054 80.076 80.096 20.113 90.185 80.242 10.287 90.326 1
    1.250.201 30.130 10.078 40.036 50.031 30.058 00.081 20.102 10.121 50.199 90.259 80.307 20.346 0
    1.500.201 90.131 70.080 00.037 20.032 40.060 10.084 60.106 50.126 40.208 10.271 40.321 30.361 7
    2.000.196 50.130 10.080 40.038 10.033 70.063 10.088 90.112 20.133 50.219 60.284 90.336 00.376 7
    2.500.195 70.132 50.082 40.039 20.035 00.065 40.092 50.117 20.139 90.232 20.299 50.351 30.390 6
    3.000.190 20.130 30.082 10.039 50.035 40.066 60.094 40.119 60.142 40.234 60.302 10.352 00.390 3
    3.500.194 90.135 90.086 00.041 20.036 90.069 50.098 40.124 70.148 30.243 00.309 70.358 20.395 1
    4.000.187 00.132 20.084 80.040 80.037 00.069 80.099 20.125 70.149 50.242 60.307 10.353 00.387 1
    4.500.185 70.132 60.085 00.041 10.037 00.069 50.098 50.124 50.147 90.239 30.301 50.345 30.378 0
    5.000.189 10.135 90.087 40.042 10.037 90.070 50.099 40.125 20.148 30.237 20.296 40.337 80.368 3
    下载: 导出CSV

    表  5   阻尼修正系数模型的事件间残差标准差τ

    Table  5   Between-event standard deviation τ of DMF model

    T/sτ
    ζ＝1%ζ＝2%ζ＝3%ζ＝4%ζ＝6%ζ＝7%ζ＝8%ζ＝9%ζ＝10%ζ＝15%ζ＝20%ζ＝25%ζ＝30%
    0.030.053 10.004 90.006 30.002 50.000 00.002 20.004 40.006 70.009 10.011 70.026 10.042 60.060 3
    0.040.100 10.056 90.030 90.018 60.011 00.020 50.036 20.035 30.041 50.064 00.078 60.089 10.097 1
    0.050.086 70.050 10.028 40.019 40.011 30.020 90.029 10.036 40.043 00.067 70.084 40.097 40.107 6
    0.060.071 00.043 30.041 40.018 60.015 40.018 60.040 00.033 50.040 10.066 90.086 20.101 20.112 7
    0.070.062 10.039 30.039 00.017 80.014 80.018 00.039 70.033 90.040 60.068 00.088 30.103 50.114 9
    0.080.053 80.056 80.034 00.016 00.013 30.016 70.036 10.031 70.038 30.066 30.086 00.100 50.111 4
    0.090.044 70.050 50.031 20.014 90.007 40.014 30.034 30.027 00.033 70.060 60.078 90.092 20.101 7
    0.100.050 10.053 40.033 10.015 10.007 50.014 10.033 20.041 70.031 60.053 60.069 10.080 80.088 8
    0.120.044 00.027 60.028 50.008 10.011 60.021 30.029 40.036 70.028 20.046 10.058 30.066 90.073 3
    0.140.051 80.031 10.028 70.013 00.010 90.019 50.025 90.031 50.035 80.053 50.042 10.050 20.057 5
    0.150.052 30.033 30.031 00.007 90.011 70.021 10.015 70.036 40.042 60.062 50.075 90.051 70.058 7
    0.160.048 60.030 50.029 10.006 80.012 00.021 40.029 40.036 30.042 10.063 20.076 70.050 60.057 5
    0.180.049 50.030 70.028 50.011 90.010 00.018 20.025 30.031 50.036 80.057 40.071 00.051 00.057 7
    0.200.050 00.031 00.027 90.013 00.010 40.019 00.015 30.032 00.037 20.057 20.070 40.051 60.059 5
    0.250.053 60.036 40.028 70.013 50.011 20.020 10.016 70.020 70.039 00.040 40.053 60.066 10.079 4
    0.300.053 80.035 30.028 60.013 00.010 40.018 40.024 50.029 50.034 40.037 60.052 40.067 60.084 0
    0.350.045 90.050 10.028 50.006 80.010 10.018 30.013 40.032 40.038 40.061 40.050 70.065 60.083 0
    0.400.049 30.053 10.030 30.007 20.011 30.010 00.014 10.036 30.042 80.038 60.055 70.073 70.093 7
    0.450.050 50.034 20.025 40.012 20.009 40.017 80.017 00.021 60.037 80.047 10.066 30.086 90.108 7
    0.500.051 60.032 50.028 50.013 20.011 00.020 10.027 70.034 70.041 10.052 30.076 90.101 00.125 5
    0.600.056 40.037 70.031 90.015 40.008 00.015 20.021 70.037 20.034 70.064 80.094 30.123 30.152 8
    0.700.060 50.039 10.035 20.010 80.013 20.016 80.034 00.032 20.039 60.075 30.110 60.144 90.179 7
    0.800.060 80.038 90.035 50.010 70.014 10.019 20.038 60.037 00.045 70.086 30.125 10.161 90.199 3
    0.900.062 20.037 90.037 30.010 30.014 80.018 20.039 30.035 40.044 10.088 40.131 00.171 50.211 1
    1.000.069 70.044 80.040 70.019 00.011 30.021 60.031 90.041 80.051 70.098 60.143 80.187 30.229 1
    1.250.067 60.049 90.038 50.018 60.012 80.024 50.036 00.047 50.058 70.115 00.168 30.219 50.266 2
    1.500.078 10.057 10.044 70.017 10.016 00.031 50.046 00.060 70.075 30.142 60.205 20.259 50.309 3
    2.000.111 80.082 00.050 90.024 20.022 30.043 50.063 10.082 20.101 60.190 20.265 20.329 10.381 4
    2.500.123 00.091 00.057 70.027 80.026 50.051 90.076 00.098 90.121 20.222 10.303 30.370 00.423 9
    3.000.141 40.103 90.066 40.032 00.030 40.059 10.086 80.112 90.138 00.248 50.334 60.401 40.453 5
    3.500.149 60.111 20.071 80.035 30.034 10.066 20.096 00.124 50.152 60.269 60.357 90.425 60.476 6
    4.000.163 60.121 10.078 20.037 70.035 90.070 10.102 40.133 30.162 00.282 90.371 40.436 50.485 8
    4.500.179 50.132 30.085 30.041 40.039 30.076 70.111 90.145 00.176 00.301 70.392 60.457 50.504 5
    5.000.185 60.138 70.091 30.044 60.042 20.081 90.118 80.152 80.185 00.311 70.400 70.463 10.507 5
    下载: 导出CSV
    • 参考文献(25)
  • 郝安民,周德源,李亚明,张晖. 2012. 考虑震级影响的规范阻尼修正系数评估[J]. 同济大学学报(自然科学版),40(5):657–661.

    Hao A M,Zhou D Y,Li Y M,Zhang H. 2012. Evaluation of damping modification factors in codes with a consideration of effect of earthquake magnitude[J]. Journal of Tongji University (Natural Science),40(5):657–661 (in Chinese).
    蒋建,吕西林,周颖,蒋欢军. 2009. 考虑场地类别的阻尼比修正系数研究[J]. 地震工程与工程振动,29(1):153–161.

    Jiang J,Lü X L,Zhou Y,Jiang H J. 2009. Research on modification factors of damping ratios considering site conditions[J]. Journal of Earthquake Engineering and Engineering Vibration,29(1):153–161 (in Chinese).

    Abrahamson N A,Youngs R R. 1992. A stable algorithm for regression analyses using the random effects model[J]. Bull Seismol Soc Am,82(1):505–510. doi: 10.1785/BSSA0820010505

    Ambraseys N N,Douglas J. 2003. Near-field horizontal and vertical earthquake ground motions[J]. Soil Dyn Earthq Eng,23(1):1–18. doi: 10.1016/S0267-7261(02)00153-7

    Bozorgnia Y,Campbell K W. 2004. The vertical-to-horizontal response spectral ratio and tentative procedures for developing simplified V/H and vertical design spectra[J]. J Earthq Eng,8(2):175–207.

    Brillinger D R,Preisler H K. 1984. An exploratory analysis of the Joyner-Boore attenuation data[J]. Bull Seismol Soc Am,74(4):1441–1450.

    Japan Road Association. 1980. Specifications for Highway Bridges. Part V, Seismic Design[S]. Tokyo: Maruzen Company Limited: 24–25.

    Jiang F,Zhao J X. 2017. A ground‐motion prediction equation for vertical spectra of the strong‐motion records from the subduction slab events in Japan using site class as the site term[J]. Bull Seismol Soc Am,107(5):2328–2341. doi: 10.1785/0120160387

    Li H,Chen F. 2017. Damping modification factors for acceleration response spectra[J]. Geodesy Geodyn,8(5):361–370. doi: 10.1016/j.geog.2017.04.009

    Lin Y Y,Chang K C. 2003. Study on damping reduction factor for buildings under earthquake ground motions[J]. J Struct Eng,129(2):206–214. doi: 10.1061/(ASCE)0733-9445(2003)129:2(206)

    Lin Y Y,Chang K C. 2004. Effects of site classes on damping reduction factors[J]. J Struct Eng,130(11):1667–1675. doi: 10.1061/(ASCE)0733-9445(2004)130:11(1667)

    Newmark N M, Hall W J. 1982. Earthquake Spectra and Design[M]. Berkeley: Earthquake Engineering Research Institute: 1–103.

    Rezaeian S,Bozorgnia Y,Idriss I M,Abrahamson N,Campbell K,Silva W. 2014. Damping scaling factors for vertical elastic response spectra for shallow crustal earthquakes in active tectonic regions[J]. Earthq Spectra,30(3):1335–1358. doi: 10.1193/100512EQS298M

    Xiang Y,Huang Q L. 2019. Damping modification factor for the vertical seismic response spectrum:A study based on Japanese earthquake records[J]. Eng Struct,179:493–511. doi: 10.1016/j.engstruct.2018.11.021

    Zhao J X,Irikura K,Zhang J,Fukushima Y,Somerville P G,Asano A,Ohno Y,Oouchi T,Takahashi T,Ogawa H. 2006a. An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio[J]. Bull Seismol Soc Am,96(3):914–925. doi: 10.1785/0120050124

    Zhao J X,Zhang J,Asano A,Ohno Y,Oouchi T,Takahashi T,Ogawa H,Irikura K,Thio H K,Somerville P G,Fukushima Y,Fukushima Y. 2006b. Attenuation relations of strong ground motion in Japan using site classification based on predominant period[J]. Bull Seismol Soc Am,96(3):898–913. doi: 10.1785/0120050122

    Zhao J X,Zhou S L,Gao P J,Long T,Zhang Y B,Thio H K,Lu M,Rhoades D A. 2015. An earthquake classification scheme adapted for Japan determined by the goodness of fit for ground-motion prediction equations[J]. Bull Seismol Soc Am,105(5):2750–2763. doi: 10.1785/0120150013

    Zhao J X,Zhou S L,Zhou J,Zhao C,Zhang H,Zhang Y B,Gao P J,Lan X W,Rhoades D,Fukushima Y,Somerville P G,Irikura K. 2016a. Ground-motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bull Seismol Soc Am,106(4):1552–1569. doi: 10.1785/0120150063

    Zhao J X,Liang X,Jiang F,Xing H,Zhu M,Hou R B,Zhang Y B,Lan X W,Rhoades D A,Irikura K,Fukushima Y,Somerville P G. 2016b. Ground-motion prediction equations for subduction interface earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bull Seismol Soc Am,106(4):1518–1534. doi: 10.1785/0120150034

    Zhao J X,Jiang F,Shi P,Xing H,Huang H F,Hou R B,Zhang Y B,Yu P C,Lan X W,Rhoades D A,Somerville P G,Irikura K,Fukushima Y. 2016c. Ground-motion prediction equations for subduction slab earthquakes in Japan using site class and simple geometric attenuation functions[J]. Bull Seismol Soc Am,106(4):1535–1551. doi: 10.1785/0120150056

    Zhao J X,Jiang F,Ma Y,Zhou J,Cheng Y,Chang Z W. 2017. Ground‐motion prediction equations for the vertical component from shallow crustal and upper‐mantle earthquakes in Japan using site classes as the site term[J]. Bull Seismol Soc Am,107(5):2310–2327. doi: 10.1785/0120160376

    Zhao J X,Yang Q S,Su K W,Liang J G,Zhou J,Zhang H,Yang X G. 2019. Effects of earthquake source,path,and site conditions on damping modification factor for the response spectrum of the horizontal component from subduction earthquakes[J]. Bull Seismol Soc Am,109(6):2594–2613. doi: 10.1785/0120190105

    Zhou J,Zhao J X. 2020. A damping modification factor prediction model for horizontal displacement spectrum from subduction interface earthquakes in Japan accounting for site conditions[J]. Bull Seismol Soc Am,110(3):1231–1246. doi: 10.1785/0120190275
    • 相关文章
    • 施引文献
    • 资源附件(0)
图(9)  /  表(5)
计量
  • 文章访问数:  419
  • HTML全文浏览量:  162
  • PDF下载量:  21
  • 被引次数: 0
出版历程
  • 收稿日期:  2020-12-02
  • 修回日期:  2021-05-25
  • 网络出版日期:  2022-04-23
  • 发布日期:  2022-04-23

目录

摘要
HTML全文
    参考文献(25)
    相关文章
    施引文献
    资源附件(0)

    /

    返回文章
    返回

    本系统由 北京仁和汇智信息技术有限公司 开发  技术支持：info@rhhz.net 百度统计