S wave envelope synthesis based on different scattering patterns
-
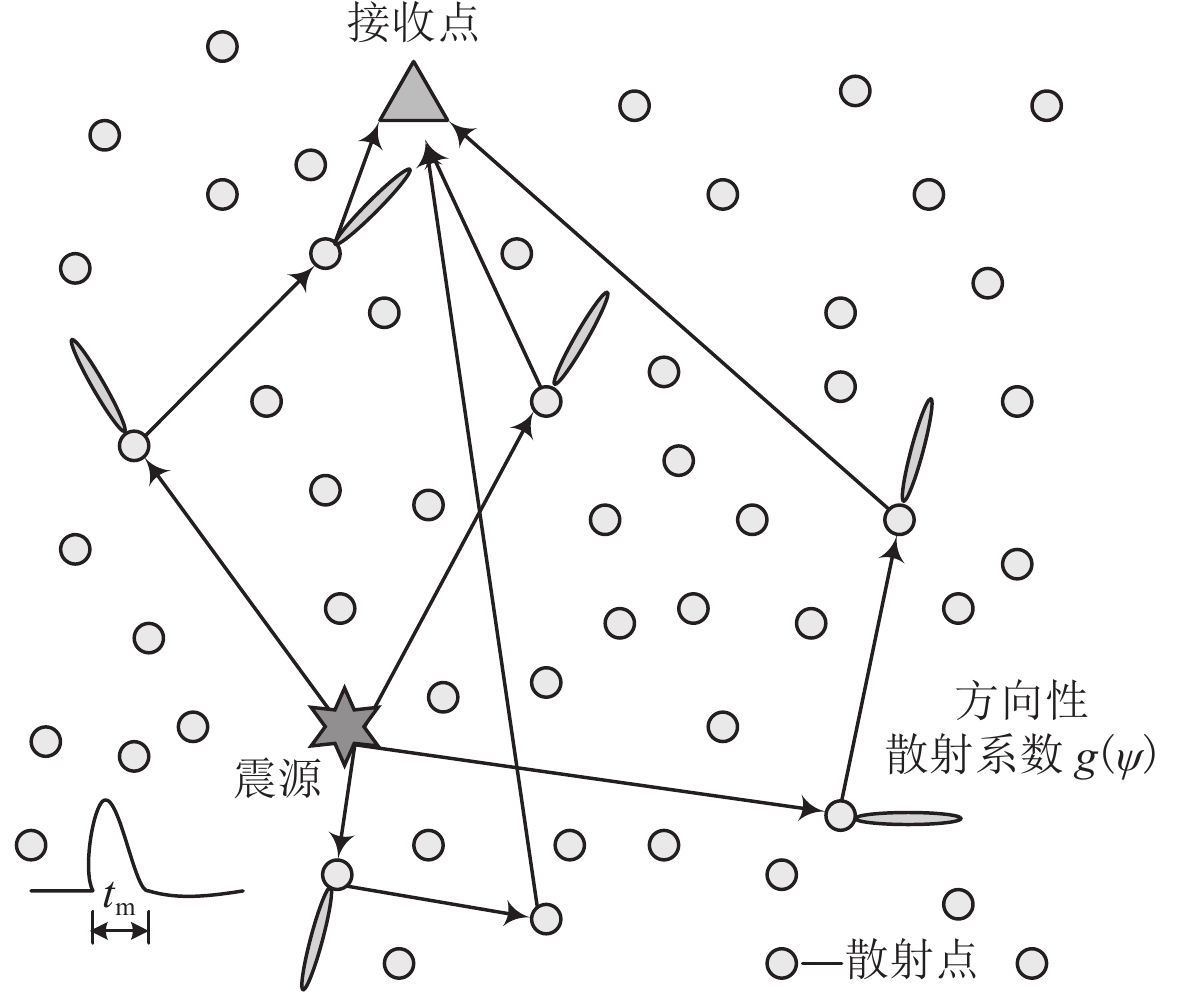
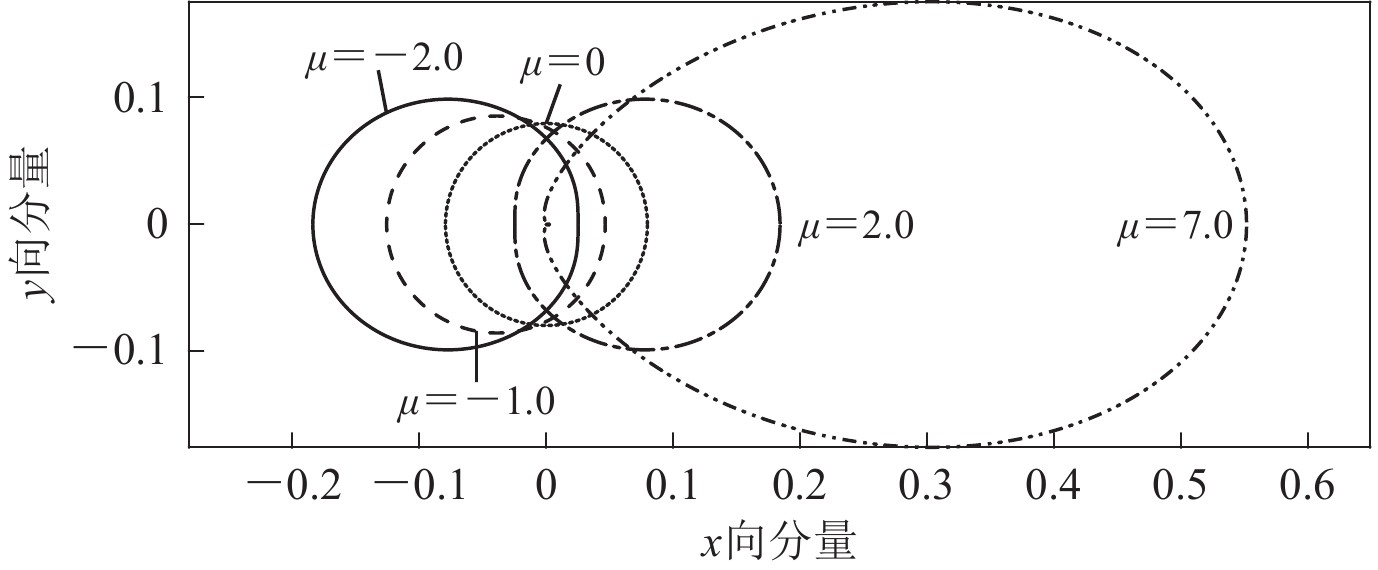
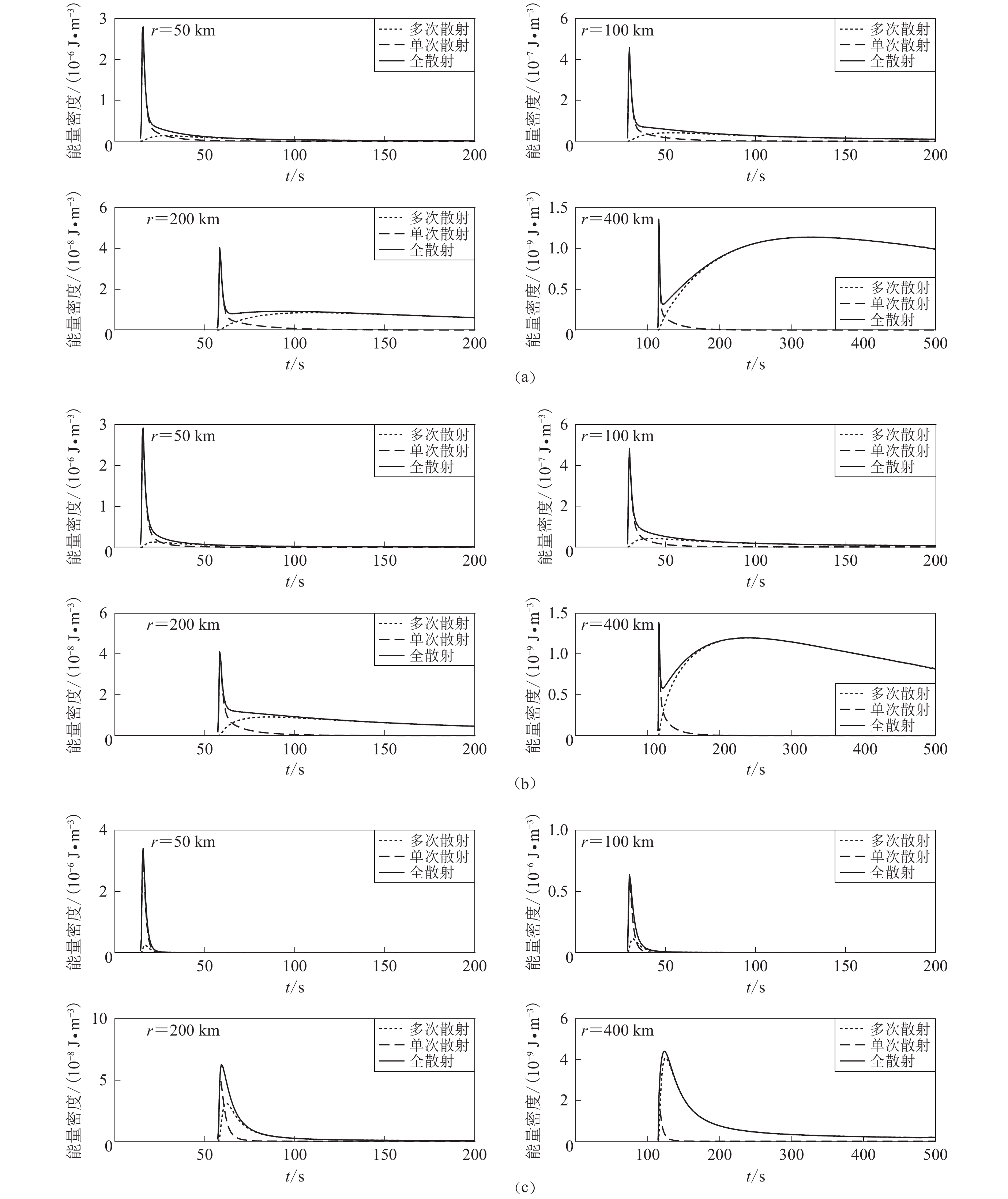
摘要: 为揭示地震波在地壳小尺度非均匀介质中的散射过程，更准确地描述地震波的包络展宽现象，本文基于多次各向异性散射理论，采用离散波数法求解能量密度积分方程，选取高斯型自相关函数表征的散射模式，得到S波能量密度包络。基于此，本文首先分析了单次散射和多次散射在形成S波能量密度包络中的贡献规律；然后探讨了吸收系数和总散射系数对合成S波能量密度包络的影响；最后对比了在不同散射模式下合成的S波能量密度包络的差异。结果显示：① 不同的散射模式下单次散射和多次散射对地震波散射过程的贡献规律是一致的，对于近震（震源距小于100 km），单次散射模型可以近似合成S波能量密度包络；随着震源距增大，多次前散射模型可以更快地接近总能量密度包络；② 吸收系数增大会降低直达S波和尾波幅值，总散射系数增大会降低直达S波幅值，但使得S波尾波幅值升高；③ 前散射模式下S波能量密度包络随震源距的增大会导致峰值延迟，包络展宽，尾波衰减一致性更快等现象产生。Abstract: In order to reveal the scattering process of seismic waves in the small scale inhomogeneous medium of the crust and to describe the envelopment broadening phenomenon of seismic waves more accurately, a discrete wave-number method is used to solve the improved seismic wave energy density integral equation based on the multiple anisotropic scattering theory, and the scattering pattern represented by Gaussian autocorrelation function is selected to obtain the S wave energy density envelope. Firstly, we analyzed the contribution of single scattering and multiple scattering to the energy density envelope of S wave. Then, we discussed the effects of absorption coefficient and total scattering coefficient on the synthesis of S wave energy density envelope. Finally, we compared the differences of the energy density envelope of S wave synthesized in different scattering patterns. The results show that: ① The contribution of single scattering and multiple scattering to the seismic wave scattering process is consistent, and for the near earthquakes （hypocentral distance is less than 100 km）, the single scattering model can be used to match the S-wave energy density envelope. As the hypocentral distance increases, the multiple forward scattering pattern can approach the total energy density envelope more quickly. ② As the absorption coefficient increases, the amplitude of the direct S wave and the coda wave will decrease. And when the total scattering coefficient increases, the amplitude of the direct S wave will decrease, while the coda wave amplitude of the S wave will increase. ③ In the forward scattering pattern, with the increase of hypocentral distance, the energy density envelope of S-wave appears the peak delay, the envelope is widened, and the attenuation consistency of the coda wave is accelerated.
-
Keywords:
- anisotropic /
- scattering theory /
- Gaussian medium /
- forward scattering pattern /
- the S wave envelope
-
引言
地震前的地电场异常变化是非常重要的地震前兆信号，这类地震前的异常变化在我国被称为震前地电场异常变化(赵玉林，钱复业，1981；钱复业等，1998；陈有发等，1999；毛桐恩等，1999；马钦忠, 2008a, b)，20世纪80年代初希腊科学家将其称之为地震电信号(Varotsos, Alexopoulos, 1984a, b；Varotsos et al, 1993, 2005; Park et al, 1996; Uyeda et al, 2000, 2009; Orihara et al, 2002; Tsutsui, 2002; Telesca et al, 2004; Varotsos, 2005; 马钦忠等, 2009, 2013).由于在我国地电场观测中存在大量的干扰信息，包括人类工业活动产生的噪声、雷电噪声、电极极化噪声等，因此在寻找地震电信号时往往由于噪声排除不彻底，使所获得的地震前的地电场异常变化或地震电信号的可信度降低，也因此在研究震前地电场前兆变化特征时难免将噪声信号作为研究对象，导致对地电场前兆变化特征的认识出现了偏差，例如用地电场长、短极距比值法研究震前地电场异常变化特征时就会出现这样的问题.为了避免类似问题，利用人工源强电流信号作为信号源来研究地电场变化特征，这是因为信号源和地电场观测台站的位置均是确定的.不同地区的震前地电场异常变化存在时空分布的差异，准确地认识这些差异性有赖于更加深入的研究.由于不同地震的震中区域往往属于不同的地震断裂构造带，因而孕震过程和介质条件也不同，地震电信号的特征也呈现出复杂性，要更加准确地认识地震前地电场前兆信号的远距离传播特征、选择性特征及“敏感点”等问题依然是目前面临的重要任务.不同地区地电场的空间变化特征差异很大，主要原因为不同地区的地质构造、断裂带的分布规模和走向及地下电性结构均相差很大，且不同区域地电场观测网中每个台站台址的电性结构也存在很大差异.为了更进一步深入地研究地电流在地下的传播特征和选择性等特征，对多个地区确定性的人工强电流源及其所在区域内分布的多个地电场观测台站的观测资料进行对比研究是非常有必要的.
本文拟通过陕甘宁晋地区、川滇地区等多个特高压输电换流站的接地极向地下注入大电流信号，观测研究各地区地电场的变化特征，对比山东地区和上海地区接地极大电流附加地电场信号的空间分布特征，揭示各地区的地电场变化的区域性差异，推进利用地震前的地震电信号进行地震短临预测和预报工作.
1. 人工源、地质条件及观测网
1) 人工源.在陕甘宁晋地区、川滇地区、山东地区及上海地区均有超、特高压直流输电换流站接地极，当电路不平衡时会向地下注入上千安培的巨大电流，最大电流可达约4700 A(马钦忠等，2016).由于同一特、高压直流输电换流站接地极的两端均相距上千千米，而本文研究区域内能够观测到信号的最大接地极距远未超过上述接地极距的一半，故本文在每个区域内只设置一个电流源.
2) 地质条件.陕甘宁晋地区存在环绕鄂尔多斯地块的断裂带，包括贺兰山断裂带、部分秦岭构造带、太行山断裂带等；云南地区主要为红河断裂带、澜沧江断裂带、怒江断裂带及小江断裂带；东部地区最大的地质断裂构造带为郯庐断裂带.
3) 地电场台站分布.本文研究区内所布设的地电场台站包括陕甘宁晋地区环绕鄂尔多斯地块边缘和川滇地区的31个地电场台站，山东半岛及其周边地区的16个地电场台站和上海及周边地区的8个地电场台站.目前我国地电场台站在建台时均采用多极距观测的方式，即在所观测的每个方向上均布设长、短极距电极，用于识别和排除噪声.常用的台站电极布设方式如图 1所示.
![]()
图 1 研究区电极布设方式示意图(a)银川、石嘴山、周至、乾陵、临汾、夏县、洱源、合阳台电极布设图; (b)罗茨、武都台电极布设图; (c)小庙、泸沽湖、祥云、盐源台电极布设图Figure 1. Electrodes layout diagram in studied area(a) The electrodes arrangement at the stations of Yinchuan, Shizuishan, Zhouzhi, Qianling, Linfen, Xiaxian, Eryuan and Heyang; (b) The electrodes arrangement at the stations of Luoci and Wudu; (c) The electrodes arrangement at the stations of Xiaomiao, Luguhu, Xiangyun and Yanyuan2. 人工源地电场变化的区域性特征分析
2.1 陕甘宁晋地区地电场变化特征
图 2为陕甘宁晋地区的人工电流源和鄂尔多斯地块边缘的地电场台站分布示意图.该研究区中人工电流源的强度为3600 A，当该电流源由接地极流入大地时，则在许多地电场台站可以观测到源自其的附加地电场信号, 且该附加地电场信号的强度和变化特征与本区地质构造密切相关.
![]()
图 2 陕甘宁晋地区地电场台站分布及大电流源位置图Figure 2. Scatter diagram of geoelectric field stations and location of a heavy current source in Shaanxi-Gansu-Ningxia-Shanxi region2016年9月18日2时16分至3时48分, 宁夏回族自治区高沙窝换流站的接地极向地下注入3600 A大电流，陕甘宁晋地区的10个地电场观测台站均记录到了此次事件. 图 3给出了陕甘宁晋地区部分地电场台站观测到的附加地电场波形图.每个台站在NS，EW，NE(NW)方向均有两个测道，即长、短极距观测.其中ENSL和ENSS分别表示NS方向地电场长、短极距电场分量，其它方向类同. 表 1给出了能够观测到该附加地电场的各台站每个分量最大幅值的观测数据.
![]()
图 3 2016年9月18日2时16分至3时48分陕甘宁晋地区部分台站观测到的附加地电场波形图Figure 3. Waveforms of the additional geoelectric field recorded at partial stations of Shaanxi-Gansu-Ningxia-Shanxi region from 02:16 to 03:48 on September 18, 2016表 1 2016年9月18日高沙窝接地极注入3600 A电流时观测到的地电场信号特征Table 1. The signal characteristics of the geoelectric field recorded at the stations when 3600 A current was injected into the underground from Gaoshawo grounding electrode on September 18, 2016台站 r/km ENSL/(mV·km-1) ENSS/(mV·km-1) EEWL/(mV·km-1) EEWS/(mV·km-1) ENWL/(mV·km-1) ENWS/(mV·km-1) 银川 90 12.0 12.6 -8.3 -8.2 14.0 14.8 石嘴山 150 4.5 4.2 -2.8 -2.7 4.8 4.2 固原 230 -2.1 -2.2 -0.5 -0.4 -1.7(ENEL) -1.8(ENES) 平凉 280 -4.5 -5.2 -10.1 -11.0 -4.0(ENEL) -4.0(ENES) 乾陵 392 -2.2 -1.9 2.4 2.1 -2.7 -2.2 凤翔 370 -2.2 -1.8 -0.4 -2.3 -1.9(ENEL) -2.7(ENES) 周至 380 0 0 0.4 0.5 -0.4 -0.4 合阳 420 0 0 1.5 1.8 0.9 2.2 临汾 440 -3.5 -1.0 3.4 0.8 -3.0 -5.7 夏县 490 -0.6 -0.5 1.5 1.5 -1.5 -1.4 注：r为信号源与观测台站间的距离. 由图 3和表 1可以看出，当高沙窝换流站接地极的大电流注入地下时，测区地电场的变化特征为：
1) 在距离信号源90—490 km范围内，随着距离信号源越远，附加地电场变化幅值衰减得越厉害，但存在远距离台站的观测幅值大于近距离台站的观测幅值的现象.距离信号源最近的银川台记录到的信号幅值最大；距离信号源150 km处的石嘴山台与距离信号源280 km处的平凉台观测到的NS和NE分量的幅值相当，但平凉台观测到的EW分量的幅值要比石嘴山台EW分量的幅值大将近5倍，也比最近的银川台观测到的EW分量大；距离信号源440 km处的山西临汾台观测到的信号幅值要比距离信号源230，370，380，392，420 km处的固原台、凤翔台、周至台、乾陵台及合阳台都要大.
2) 对于完整的方波而言，只在银川台和石嘴山台观测到了完整的方波，其它台站观测到的波形均发生了不同程度的畸变.
3) 在地电场均匀度，即长、短极距信号幅值比方面，临汾台最大可达4.2，凤翔台最大为0.17，其余台站附加地电场的均匀度均较好，即长、短极距信号幅值比约为1.
4) 能够观测到该大电流源信号的最远台站为距离信号源490 km外的山西夏县台，但在一些较近的台站却未观测到该信号，例如距离信号源150，360，390，420，480 km的中卫台、乌加河台、宝鸡台、天水台、太原台以及大电流源以西200—450 km范围内由7个台站组成的天祝地电场台阵均未观测到该信号.
2.2 西南地区地电场变化特征
图 4为川滇交界区域人工大电流源及该区地电场台站分布图.该研究区域中人工电流源的强度为4500 A，当该电流源由接地极流入大地时，该区域内许多地电场台站均可观测到该信号, 在川滇地区该信号的强度和变化特征与南北地震带南段地质构造带的分布密切相关.
![]()
图 4 川滇地区地电场台站分布及大电流源位置图Figure 4. Scatter diagram of geoelectric field stations and location of heavy current sources in Sichuan-Yunnan region图 5给出了2016年5月1日15时15分至16时45分丽江换流站接地极向大地注入3200 A的强大方波电流时川滇地区地电场观测台接收到的信号波形图. 图 6给出了元谋1台、嵩明台和曲江台记录到的该信号的脉冲波形，但脉冲波形仅在图 5所示的矩形方波开始和结束的时刻被记录到.
![]()
图 5 2016年5月1日15时15分至16时45分川滇地区台站观测到的附加地电场波形图Figure 5. Waveforms of the additional geoelectric field recorded at the stations of Sichuan-Yunnan region from 15:15 to 16:45 on May 1, 2016![]()
图 6 2016年5月1日15时15分至16时45分元谋1台、嵩明台和曲江台记录到的脉冲信号Figure 6. Pulsing signals recorded at the stations of Yuanmou one, Songming and Qujiang respectively at 15:15 and 16:45, May 1, 2016表 2给出了各台站记录到的矩形方波的相关参数，每个测道上均记录了两个数据，分别为大电流开始和结束时刻所观测到的脉冲信号幅值.
表 2 2016年5月1日丽江换流站接地极注入3200 A电流时地电场观测到的信号特征Table 2. The signal characteristics of the geoelectric field recorded at the stations when 3200 A current was injected into the underground from Lijiang grounding electrode on May 1, 2016台站 r/km ENSL/(mV·km-1) ENSS/(mV·km-1) EEWL/(mV·km-1) EEWS/(mV·km-1) ENEL/(mV·km-1) ENES/(mV·km-1) 洱源 95 48 95 44 90 60(ENWL) 128(ENWS) 祥云 122 6.0 6.1 1.4 1.5 4.1 4.0 元谋2 154 2.0 1.9 3.5 4.0 1.2 1.3 泸沽湖 125 9.1 * * * 8.0 9.3 弥渡 147 * * * * 1.9 1.9 元谋1 165 -3.4, 3.1 -3.6, 3.9 9.4, -10.4 8.9，-9.2 -9.8，9.9(ENWL) -8.8，9.1 曲江 412 -9.4, 11.6 -8.7, 14.4 9.1, -10.2 6.4，13.0 0.6，0.4 0.6，0.4 嵩明 277 -0.5, 0.5 -0.7, 0.5 -1.0, 0.8 -1.0，0.9 0.0，0.0 0.0，0.0 腾冲 270 0 0 0 0 0 0 注： *表示由于受到干扰而分辨不清附加地电场的最大幅值. 由图 5，6及表 2可以看出，当丽江换流站接地极的大电流注入地下时，测区地电场的变化特征为：
1) 在附加地电场幅值上，对于完整方波而言，距离信号源最近的洱源台记录到的信号幅值最大；距信号源125 km处的泸沽湖台在NE方向的长、短极距上记录到的信号幅值次之，虽然其在EW方向的长、短极距和NS方向短极距由于受噪声干扰而分辨不清信号；距信号源122 km处的祥云台记录到的最大信号幅值较前两个台的略小；距信号源157 km处的元谋2台的幅值最小；对于只在大电流开始和结束时刻被记录到的脉冲信号而言，距离信号源412 km的曲江台记录到的信号幅值最大，但距信号源165 km的元谋1台记录到的NW分量信号的幅值大于曲江台同向信号的幅值；而在距信号源227 km的嵩明台的信号幅值小于前两个台的脉冲信号幅值；距信号源270 km处的腾冲台未观测到该附加地电场的脉冲信号.
2) 在波形形态上，部分台站记录到了完整的方波，如表 1中的前5个台站；而有些台站只记录到了大电流开始和结束时的信息，且呈尖峰脉冲形态，如表 1中的合阳、临汾及夏县台.特别是分别位于元谋县南部和北部的元谋1台和元谋2台，两台相距虽在18 km之内，但两个台站记录到的大电流信号的波形形态相差甚远.
3) 在地电场均匀度方面，洱源台附加地电场在长极距上观测到的信号幅值要比短极距上观测到的信号幅值大一倍左右；而其余台站附加地电场的均匀度均较好，即长、短极距信号幅度比约为1.
4) 对于丽江大电流源的信号，有的台站能够记录到, 如表 1中的台站，但也存在记录不到的情况，如距离信号源分别为218，128，130 km的小庙台、红格台、盐源台均未观测到，这些台的源距r要比曲江台的小得多.
当大电流信号源的位置发生改变后，则在相同区域地电场观测网记录到的附加地电场的特征也会大不相同.例如，2012年11月26日8时20分至15时40分西昌接地极装置系统向地下注入电流强度为4500 A的电流时，在其NNE方向约10 km处的小庙台记录到了源自该接地极的附加地电场信号波形，且最大信号幅值为NS向短极距记录到的1222 mV/km，同时540 km处的重庆仙女山台也记录到了该信号开始和结束时的脉冲信号.通过多次观测与对比分析，可以得到这样的认识：对于西昌接地极的强大电流信号，川、滇、渝地区的地电观测网中(图 4)，只有距其10 km左右的小庙台和距其540 km处的仙女山台能记录到，而距其80 km以远的其它台站均未观测到(马钦忠等，2013).
2.3 其它地区大电流注入地下时测区地电场的变化特征
在本研究的前期工作中，对山东半岛地区和上海地区的人工电流源及其附加地电场的变化特征进行了研究(马钦忠等, 2014, 2016).山东半岛地区的青岛换流站接地极位于郯庐断裂带东侧，当2100 A的强大方波电流流入该地时，山东及其周边地区的11个地电场台站均接收到了该信号，且波形清晰.该区域的附加电场特征为：① 在同一台站，附加地电场幅值在不同方向存在不同程度的差异，存在符号相反的现象；② 沿着郯庐断裂带，距离信号源越远，信号强度越弱.在郯庐断裂带西侧SW方向100 km之外既已观测不到附加地电场，而在郯庐断裂带NW侧，跨断层之后在450 km处却仍可观测到附加地电场，且存在近台观测比远台观测效果差、幅值小的现象；③ 某些近台未观测到信号.上海及其周边地区有8个台站可以观测到源自江苏同里人工源大电流的附加地电场，其分布具有区域性特征：① 人工源电流强度大，为4516 A，最大观测距离偏小，为298 km；② 浦东台距人工源NE方向只有113 km，但未观测到信号；③ 在人工源NW方向，存在着远台观测(嘉山台298 km)比近台观测(海安台194 km)效果好、幅值大的现象.
3. 附加地电场空间变化的区域性差别
从上述分析可以看出, 不同地区大电流源的附加地电场的空间变化特征是不同的.
在陕甘宁晋地区，当宁夏高沙窝换流站接地极向地下注入3600 A的大电流时，在陕甘宁及山西南部地区490 km范围内的10个地电场观测台站均记录到了此次事件；沿着鄂尔多斯地块的南部边缘弧形地带分布的台站，如固原台、平凉台、凤翔台、周至台、合阳台、夏县台和临汾台均能够观测到该信号；鄂尔多斯地块的NW边缘，只有距信号源很近的银川台和石嘴山台观测到了该信号；在距离该信号源150 km的中卫台、360 km的乌加河台、390 km的宝鸡台、420 km天水台、480 km的太原台和550 km的武都台均未观测到该信号；在高沙窝大电流源以西200—450 km范围内由7个台站组成的甘肃天祝地电场台阵亦未观测到源自该大电流源的信号，这应该与贺兰山系的阻隔作用密切相关.
在川滇地区，对于源自丽江接地极的3200 A信号，在其南部和东南部观测到的附加地电场无论强度还是观测距离均远大于北部地区，例如在其SE方向，远在412 km处的曲江台站观测到了该信号；而对于西昌4500 A的大电流源信号，除了距其10 km处的小庙台和距其NE方向540 km处的仙女山台观测到了该信号外，其周围台站均未观测到该信号，包括距其仅约90 km处的盐源台.从波形上看，西南地区部分台站记录到了完整的矩形波，而也有部分台站只记录到了该矩形波开始和结束时刻的尖峰脉冲信号，特别是在元谋地区相距只有18 km的元谋1台和元谋2台，后者记录到了完整的矩形波，而前者只记录到了该矩形波在开始和结束时的尖峰脉冲.
在山东半岛及其周边地区，源自2100 A大电流的附加地电场的传播具有很强的方向性，能够记录到该信号的最远台站为距其NW方向450 km处的通州台，而在其正SW方向的台站未观测到该信号，距其南向250 km以远的台站亦未观测到此信号.可观测到信号的台站，其所观测到的信号波形均为矩形波，且波形畸变程度随着台站与信号源之间距离的增大而增大.
在上海及周边地区，对于江苏同里4516 A的大电流信号，可观测到该信号的最远台站为距其NW方向298 km处的嘉山台，但距其NE方向113 km处的浦东台站则观测不到该信号.
上述各地区均存在这一现象，即远台观测比近台观测效果好、幅值大，甚至某些近台观测不到源自人工源大电流的附加地电场.该现象与信号源至观测台站连线的方向关系密切，可将这种关系视为地电场观测中的“选择性”效应.不同地区“选择性”效应呈现的方式有所不同，其与地质构造特征密切相关，例如陕甘宁晋地区对于高沙窝大电流源而言，距其西部150 km以外的台站均未观测到信号，因在该地区横贯了NS走向的贺兰山系及大型断裂带，该山系和断裂带对地电场向西的传播起到了阻隔作用；在其南部鄂尔多斯地块的南缘边界之南是著名的近EW走向的秦岭造山系，而未观测到附加地电场信号的宝鸡台、天水台和武都台均位于秦岭构造系中，可见秦岭构造山系对地电场向南的传播也起到了阻隔作用；类似地，太原台可能由于太行山系的阻隔或其台址条件的限制而未观测到该信号.在西南地区对于丽江“源”而言，距“源”SW方向94 km处的洱源台观测到的信号幅值最大，远至其SE方向412 km的曲江台可以观测到其附加地电场信号，但在其NE方向128 km处的盐源台和218 km处的小庙台则未观测到，推测这与洱源台和曲江台均在红河断裂带附近有关；距离该信号源270 km处的腾冲台未观测到该附加地电场，这是由于在该“源”与腾冲台之间自东向西依次沿NW--SE展布红河断裂带、澜沧江断裂带及NS走向的怒江断裂带，这3条断裂带均为大型走滑断裂带，均对地电场信号有阻隔作用.在山东半岛地区由于大电流源在郯炉断裂带东侧，跨过郯炉断裂带位于“源”SW方向的台站均未观测到附加地电场信号，也呈现出大型断裂带对信号的阻隔作用.在上海及周边地区由于没有大的断裂带分布，只分布小的活动断层，因此大电流源的强度最大，但能够观测到附加地电场的最远距离却最小，可观测到同里“源”信号的最远距离为298 km.
另外，在同一地电场观测台网中，当人工电流源的位置发生改变后，各地电场台站观测到的附加地电场的变化特征随之发生改变，甚至是非常大的改变.例如在川滇地区，当大电流信号源由丽江“源”变为西昌“源”时，则大部分台站能够观测到信号的情形发生了很大改变，此时附加地电场只被距离信号源10 km处的小庙台及其NE方向540 km处的仙女山台观测到，而附近的大量台站均未观测到，且大电流的强度也由丽江“源”的3200 A增大为西昌“源”的4500 A.这一特征在上海地区南桥“源”、华新“源”、奉贤“源”及同里“源”的迁移及其附加地电场的特征变化中也很明显(马钦忠等，2016).山东地区应该也存在同样的现象，但本研究尚未找到该地区第二大电流源进行分析验证.
4. 装置系统和介质非均匀性影响
上述附加地电场的空间分布特征及其地区差异特征的主要影响因素为介质电性结构的复杂性.在同一台站，就地电场在各个方向上均匀度的影响而言，电流源与任意台站的测量极之间形成的一个特定的装置系统，这是需要考虑的因素.本文所述的大电流源向地下注入的大于2 000 A的大电流是地电场台站的测量极接收到附加电场信号的基本来源.
1) 场源实质及装置系统的影响.当点源A向地下供电的电流为I时，通常电流场在距离信号源r处的电场强度为(马钦忠等，2014)
(1) 式中：K(r)为由电流源与特定台站的特定测量极构成的装置系统参数；Q为电荷量，Q=Iρs/2π，ρs为视电阻率；在半无限均匀空间条件下，Q=Iρ/2π=2QA，ρ为电阻率, QA为电流I在接地极上积累的电荷量(曹昌祺，1961).
由此可见，当大电流源向地下注入大电流时在周围区域所产生的附加地电场实质上相当于源区电荷量为QA的点电荷在其周围地区建立的电场.从式(1) 可以看到，装置系统参数K(r)对地电场的观测影响是值得考虑的；计算表明同一台站在不同方位的电场存在差异，甚至很大的差异.
2) 区域介质结构非均匀性的影响.由上述各区域对源自人工大电流源附加地电场的空间分布特征和式(1) 可以看到，各区域存在复杂的非均匀性地下电性结构, 从而对地电场产生较大影响.在大范围区域中，ρs的差异是导致各台站之间甚至是同一个台站不同方位地电场分布特征存在差异性的重要因素之一.在局部区域, 台址地下浅层电性结构的非均匀性对地电场分布特征存在着重要影响.地电场多极距观测的目的是排除多种干扰噪声, 通常同一方向上长、短极距的地电场值基本相同，包括大小和极化方向或符号.但在实际观测中，不少台站的观测结果与此不符，主要是由于测区及附近介质电性结构的非均匀性所致，通过台站测区浅层高密度电法勘探以及对地下电性非均匀结构的数值模拟工作均可证明这种影响程度(Sarlis et al, 1999; Ma, 2002; 马钦忠，钱家栋，2003；黄清华，林玉峰，2010；马钦忠等, 2014, 2016).
陕甘宁晋地区的贺兰山断裂带、其南的秦岭断裂带、川滇地区红河断裂带、澜沧江断裂带、怒江断裂带及山东半岛的郯庐断裂带均属于大尺度范围的电性结构非均匀性地带.另外，台站测区下方的电性结构非均匀性也对附加地电场在某个方向上的均匀程度有很大影响，各台站地下电性结构的差异性是导致其观测到的电磁信号存在差异性的重要原因.基于上述原因，对于丽江接地极大电流信号，在154 km之外的元谋地区的两个相距18 km的地电场观测台站均观测到了其附加地电场，元谋2台观测到了完整的矩形波，而元谋1台只记录到该矩形波开始和结束时的尖峰脉冲，其主要原因不在于两个台站的几何参数K(r)，而在于物理参数，即视电阻率ρs，也就是说是由于这两个台站测区地下电性结构的差异性所致：元谋1台的电极埋入15 m深的基岩中，其上4—10 m为砾石层，0—4 m为黏土与沙土混合层；元谋2台的电极埋在约10 m深的黏土与沙土混合层中.
5. 讨论与结论
通过本文的研究可以看出，当在不同地区由大电流源处向地下注入3200—4600 A大电流时，在陕甘宁晋地区、川滇地区、山东半岛地区及长三角地区地电场观测网所观测到的附加地电场的空间变化特征差别很大，甚至在同一地区相同地电场观测网中当大电流源发生迁移时所观测到的附加地电场信号特征亦有很大不同.
1) 在陕甘宁晋地区，源自宁夏高沙窝3600 A大电流的信号被沿着鄂尔多斯地块南部边缘弧形地带分布的490 km范围内的10个台站观测到，在其NW边缘只有距信号源很近的银川台和石嘴山台观测到了该信号.由于贺兰山断裂带的阻隔，在距离该信号源150 km以西的中卫台和天祝地电场台阵均未观测到该信号.在秦岭构造带中分布的台站亦未观测到该信号.
2) 在川滇地区，对于丽江信号源，在其南部地区所观测到的信号强度远大于北部地区的强度，且该电场在南部地区传播的距离为412 km，也远大于其在北部地区125 km的传播距离.当信号源变为西昌大电流源时，该区只有源距10 km处的小庙台和540 km处的仙女山台观测到了信号，而在其它十几个台站均未观测到，虽然信号强度由丽江源的3200 A增大到4500 A.另外，在波形形态上，部分台站记录到了完整的方波，而部分台站只记录到了大电流开始和结束时的信息，且呈尖峰脉冲形态.
3) 在山东半岛地区，对于青岛2100 A大电流源，沿郯庐断裂SW方向250 km处的新沂台是能够观测到该信号的最远台站，而NE方向是渤海湾，没有观测资料, 且辽宁省布设的台站未观测到该信号.在郯庐断裂带NW侧，跨断层之后在450 km处的通州台还可观测到附加地电场，且存在近台观测比远台观测效果差、幅值小的现象.沿着信号源的SW方向，信号在跨过郯庐断裂带之后则无法观测到.
4) 在长三角地区，人工源电流为4516 A，强度大，最大观测距离偏小，为298 km；浦东台只距离人工源NE 113 km，但未观测到信号；在源的NW方向，存在着远台观测比近台观测效果好、幅值大的现象.在该地区，当源位置迁移后该地区地电场观测网中的信号特征发生了明显变化.
5) 对于上述地区，源自大电流源的信号波形均存在着随台站与信号源距离的增加而畸变程度增高的现象.
对于上述源自大电流源的信号在各个区域的变化特征，通过在电流源及装置系统、区域介质结构非均匀性因素对地电场观测的影响等方面进行解释，以期加深对地电场变化特征的认识，特别是为探索不同地区不同地电场的变化特征提供有益的参考，以推动地震电信号的研究.
-
![]()
图 6 不同散射模式下吸收系数ηi和总散射系数g0对S波能量密度包络合成的影响
Figure 6. Influence of absorption coefficient and total scattering coefficient on the synthesis of S wave energy density envelope under different scattering patterns
![]()
![]()
图 2 引入震源特征时间函数的辐射传输理论示意图
Figure 2. The schematic view of radiative transfer theory with the source characteristic time function
![]()
图 3 直达波 （a）、单次散射波 （b）、多次散射波 （c）的示意图
Figure 3. The schematic view of direct wave， single scattering wave and multiple scattering wave
![]()
图 5 高斯型散射模式表征系数μ取为−2.0 （a），0 （b）和7.0 （c）时不同震源距r的散射结果比较
Figure 5. Comparison of scattering results at different hypocentral distances r when the Gaussian scattering pattern characterization coefficient μ＝−2.0 （a），μ＝0 （b） and μ＝7.0 （c）
![]()
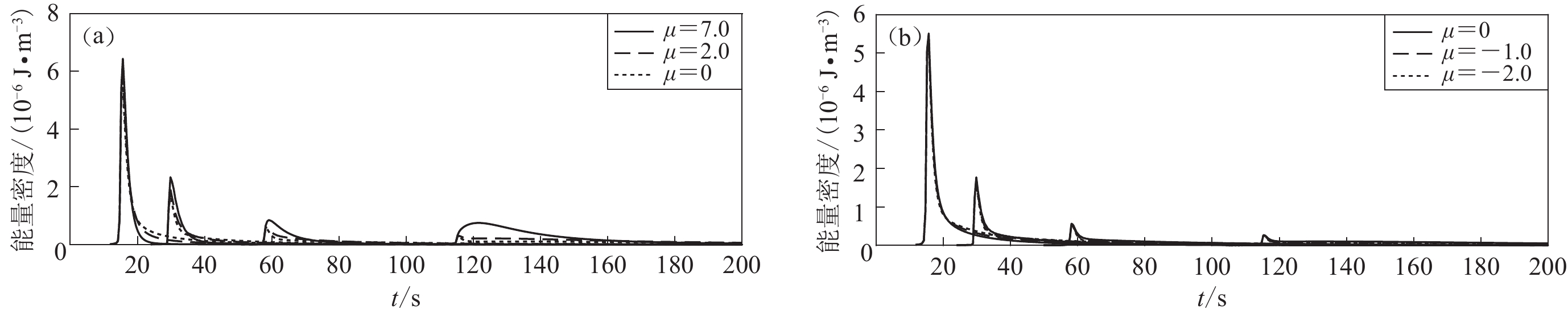
图 7 不同散射模式下合成的S波能量密度包络
（a） 前散射和各向同性散射模式；（b） 各向同性散射和后散射模式。图中纵坐标均为S波能量密度乘震源距系数exp （tS/15）后的结果
Figure 7. The energy density envelope of S wave synthesized in different scattering patterns
（a） The forward scattering and isotropic scattering patterns；（b） The isotropic scattering and back scattering patterns。The ordinates in the figure are the results of S-wave energy density multiplied by hypocentral distance coefficient exp （tS/15）
![]()
图 8 不同散射模式下合成的 S 波能量密度包络衰减一致性
（a） 各向同性散射模式； （b） 后散射模式；（c） 前散射模式
Figure 8. The consistance of the energy density envelope attenuation for the S wave synthesized in different scattering patterns
（a） The isotropic scattering pattern； （b） The back scattering pattern； （c） The forward scattering pattern
-
范小平,李清河,杨从杰,何海兵,金淑梅. 2009. 长白山天池火山区介质非均匀性[J]. 地球物理学报,52(10):2580–2587. doi: 10.3969/j.issn.0001-5733.2009.10.017 Fan X P,Li Q H,Yang C J,He H B,Jin S M. 2009. Medium inhomogeneity of crust in Changbaishan Tianchi volcano[J]. Chinese Journal of Geophysics,52(10):2580–2587 (in Chinese).
景月岭,Zeng Y H,林皋,Chen G D,李建波. 2012. 多次各向异性散射模式对S波能量密度包络曲线的影响[J]. 地球物理学报,55(6):1993–2003. doi: 10.6038/j.issn.0001-5733.2012.06.021 Jing Y L,Zeng Y H,Lin G,Chen G D,Li J B. 2012. The effect of multiple anisotropic scattering pattern on S wave energy density envelope[J]. Chinese Journal of Geophysics,55(6):1993–2003 (in Chinese).
聂永安,曾健,冯德益. 1995. 三维尾波散射问题的理论研究[J]. 地震学报,17(1):68–71. Nie Y A,Zeng J,Feng D Y. 1995. A theoretical study on the problem of 3-D wake scattering[J]. Acta Seismologica Sinica,17(1):68–71 (in Chinese).
邵婕,唐杰,孙成禹. 2016. 地震波散射理论及应用研究进展[J]. 地球物理学进展,31(1):334–343. doi: 10.6038/pg20160139 Shao J,Tang J,Sun C Y. 2016. Progress of seismic wave scattering theory and application[J]. Progress in Geophysics,31(1):334–343 (in Chinese).
曾健,聂永安. 1989. 单次与多次散射对地方震尾波的作用[J]. 地震学报,11(1):12–23. Zeng J,Nie Y A. 1989. The effects of single and multiple scattering on coda waves for local earthquakes[J]. Acta Seismologica Sinica,11(1):12–23 (in Chinese).
Aki K. 1969. Analysis of the seismic coda of local earthquakes as scattered waves[J]. J Geophys Res,74(2):615–631. doi: 10.1029/JB074i002p00615
Aki K,Chouet B. 1975. Origin of coda waves:Source,attenuation,and scattering effects[J]. J Geophys Res,80(23):3322–3342. doi: 10.1029/JB080i023p03322
Bouchon M. 1979. Discrete wave number representation of elastic wave fields in three-space dimensions[J]. J Geophys Res,84(B7):3609–3614. doi: 10.1029/JB084iB07p03609
Bouchon M. 2003. A review of the discrete wave number method[J]. Pure Appl Geophys,160(3):445–465. doi: 10.1007/PL00012545
Calvet M,Margerin L. 2013. Lapse-time dependence of coda Q:Anisotropic multiple-scattering models and application to the Pyrenees[J]. Bull Seismol Soc Am,103(3):1993–2010. doi: 10.1785/0120120239
Gusev A A,Abubakirov I R. 1987. Monte-Carlo simulation of record envelope of a near earthquake[J]. Phys Earth Planet Inter,49(1/2):30–36.
Gusev A A,Abubakirov I R. 1996. Simulated envelopes of non-isotropically scattered body waves as compared to observed ones:Another manifestation of fractal heterogeneity[J]. Geophys J Int,127(1):49–60. doi: 10.1111/j.1365-246X.1996.tb01534.x
Hoshiba M. 1991. Simulation of multiple-scattered coda wave excitation based on the energy conservation law[J]. Phys Earth Planet Inter,67:123–136. doi: 10.1016/0031-9201(91)90066-Q
Hoshiba M. 1995. Estimation of nonisotropic scattering in western Japan using coda wave envelopes:Application of a multiple nonisotropic scattering model[J]. J Geophys Res,100(B1):645–657. doi: 10.1029/94JB02064
Imperatori W,Mai P M. 2012. Sensitivity of broad-band ground-motion simulations to earthquake source and Earth structure variations:An application to the Messina Straits (Italy)[J]. Geophys J Int,188(3):1103–1116. doi: 10.1111/j.1365-246X.2011.05296.x
Imperatori W,Mai P M. 2013. Broad-band near-field ground motion simulations in 3-dimensional scattering media[J]. Geophys J Int,192(2):725–744. doi: 10.1093/gji/ggs041
Jing Y L,Zeng Y H,Lin G. 2014. High-frequency seismogram envelope inversion using a multiple nonisotropic scattering model:Application to aftershocks of the 2008 Wells earthquake[J]. Bull Seismol Soc Am,104(2):823–839. doi: 10.1785/0120120334
Margerin L. 2017. Computation of Green’s function of 3-D radiative transport equations for non-isotropic scattering of P and unpolarized S waves[J]. Pure Appl Geophys,174(11):4057–4075. doi: 10.1007/s00024-017-1621-z
Sato H. 1977. Energy propagation including scattering effects single isotropic scattering approximation[J]. J Phys Earth,25(1):27–41. doi: 10.4294/jpe1952.25.27
Sato H. 1994. Formulation of the multiple non-isotropic scattering process in 2-D space on the basis of energy-transport theory[J]. Geophys J Int,117(3):727–732. doi: 10.1111/j.1365-246X.1994.tb02465.x
Sato H. 1995. Formulation of the multiple non-isotropic scattering process in 3-D space on the basis of energy transport theory[J]. Geophys J Int,121(2):523–531. doi: 10.1111/j.1365-246X.1995.tb05730.x
Wegler U,Korn M,Przybilla J. 2006. Modeling full seismogram envelopes using radiative transfer theory with born scattering coefficients[J]. Pure Appl Geophys,163(2):503–531.
Wu R S. 1985. Multiple scattering and energy transfer of seismic waves–separation of scattering effect from intrinsic attenuation-I:Theoretical modelling[J]. Geophys J R Astr Soc,82(1):57–80. doi: 10.1111/j.1365-246X.1985.tb05128.x
Wu R S,Aki K. 1988. Multiple scattering and energy transfer of seismic waves-separation of scattering effect from intrinsic attenuation. II. Application of the theory to Hindu Kush region[J]. Pure Appl Geophys,128(1):49–80.
Zeng Y H,Su F,Aki K. 1991. Scattering wave energy propagation in a random isotropic scattering medium 1:Theory[J]. J Geophys Res,96(B1):607–619. doi: 10.1029/90JB02012
Zeng Y H. 1993. Theory of scattered P- and S-wave energy in a random isotropic scattering medium[J]. Bull Seismol Soc Am,83(4):1264–1276. doi: 10.1785/BSSA0830041264
Zeng Y H. 2017. Modeling of high frequency seismic wave scattering and propagation using radiative transfer theory[J]. Bull Seismol Soc Am,107(6):2948–2962. doi: 10.1785/0120160241
-
期刊类型引用(13)
1. 张宇，王兰炜，胡哲，张兴国，娄晓宇. 点源干扰源定位方法及其在地电场观测中的实际应用. 地震学报. 2024(01): 106-119 . 
本站查看
2. 李钟慧，王兰炜，张宇，张兴国，蒋延林，张秀霞. 高压直流输电对地电场观测影响特征分析. 高电压技术. 2024(03): 1244-1251 . 百度学术
3. 贾思超 ，赵文舟 ，吴珊珊 ，李伟 ，裴晓 ，方国庆 . 关于青浦金泽台地电场观测所受干扰的研究. 科技与创新. 2023(12): 1-7+10 . 百度学术
4. 何学秋，孙晓磊，殷山，宋大钊，邱黎明，童永军，王桥，李杰. 岩石破坏过程磁场效应实验研究及其对地震预报的意义. 地球物理学报. 2023(11): 4609-4624 . 百度学术
5. 赵文舟，马钦忠，李伟，周江南. 人工源地电场“选择性”现象研究. 地球物理学报. 2022(05): 1742-1752 . 百度学术
6. 赵文舟，李伟，温燕林，陈迁. 高压直流输电入地电流对地电场观测设施的腐蚀分析. 地震地磁观测与研究. 2022(02): 46-53 . 百度学术
7. Guoze ZHAO，Xuemin ZHANG，Juntao CAI，Yan ZHAN，Qinzhong MA，Ji TANG，Xuebin DU，Bing HAN，Lifeng WANG，Xiaobin CHEN，Qibin XIAO，Xiangyu SUN，Zeyi DONG，Jijun WANG，Jihong ZHANG，Ye FAN，Tao YE. A review of seismo-electromagnetic research in China. Science China(Earth Sciences). 2022(07): 1229-1246 . 必应学术
8. 赵国泽，张学民，蔡军涛，詹艳，马钦忠，汤吉，杜学彬，韩冰，王立凤，陈小斌，肖骑彬，孙翔宇，董泽义，王继军，张继红，范晔，叶涛. 中国地震电磁研究现状和发展趋势. 中国科学:地球科学. 2022(08): 1499-1515 . 百度学术
9. 章鑫，范晔，叶青，钱银苹. HVDC入地电流对地电场的影响规律及入地极定位. 地震地质. 2022(03): 718-735 . 百度学术
10. 罗词建. 宝德线高压直流输电附加电场变化特征. 华北地震科学. 2021(04): 95-103 . 百度学术
11. 张波，谭大诚，罗娜，尹小兵，吴鹤帅. 高压直流输电对大柏舍台地电场观测干扰的分析. 地震. 2020(01): 140-150 . 百度学术
12. 罗词建，王秋宁，李媛媛，王军儒，刘伟. 高压直流输电对陕西地电场观测的影响. 华北地震科学. 2019(03): 81-88 . 百度学术
13. 马钦忠. 与2008年汶川M_S8.0地震有关的成都台地电场异常信号. 地震学报. 2018(03): 351-363 . 本站查看
其他类型引用(2)
下载:
计量
- 文章访问数: 527
- HTML全文浏览量: 183
- PDF下载量: 62
- 被引次数: 15
