高级搜索

基于自适应噪声完全集合经验模态分解算法和Hurst指数的地震数据去噪方法

毛世榕, 史水平, 玉壮基, 苏梅艳, 李莎, 何嘉幸, 符衡, 张清

毛世榕，史水平，玉壮基，苏梅艳，李莎，何嘉幸，符衡，张清. 2023. 基于自适应噪声完全集合经验模态分解算法和Hurst指数的地震数据去噪方法. 地震学报，45（2）：258−270. DOI: 10.11939/jass.20210165
引用本文: 毛世榕，史水平，玉壮基，苏梅艳，李莎，何嘉幸，符衡，张清. 2023. 基于自适应噪声完全集合经验模态分解算法和Hurst指数的地震数据去噪方法. 地震学报，45（2）：258−270. DOI: 10.11939/jass.20210165
shu
Mao S R，Shi S P，Yu Z J，Su M Y，Li S，He J X，Fu H，Zhang Q. 2023. A seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise and Hurst exponent. Acta Seismologica Sinica，45（2）：258−270. DOI: 10.11939/jass.20210165
Citation: Mao S R，Shi S P，Yu Z J，Su M Y，Li S，He J X，Fu H，Zhang Q. 2023. A seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise and Hurst exponent. Acta Seismologica Sinica，45（2）：258−270. DOI: 10.11939/jass.20210165
shu

基于自适应噪声完全集合经验模态分解算法和Hurst指数的地震数据去噪方法

  • 中国南宁 530022 广西壮族自治区地震局

基金项目: 中国地震局监测、预备、科研三结合课题（3JH-2021036）资助
详细信息
    通讯作者:

    毛世榕，硕士，工程师，主要从事地震监测预报研究，e-mail：232529840@qq.com

  • 中图分类号: P315.61

A seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise and Hurst exponent

  • Earthquake Agency of Guangxi Zhuang Autonomous Region，Nanning 530022，China

摘要

    摘要
  • 摘要: 在地震观测中，地震数据中普遍包含有噪声信号。由于噪声信号的干扰，地震分析的效率会受到不同程度的影响。传统的去噪方法通常需要噪声的先验知识，并且滤波时会造成部分有效信号丢失。针对这一问题，本文提出一种将自适应噪声完全集合经验模态分解（CEEMDAN）算法与Hurst指数相结合的地震数据去噪方法。首先通过CEEMDAN方法将信号分解为一系列本征模函数（IMF），然后利用Hurst指数对滤波后的IMF分量进行识别，最后对地震数据IMF分量进行重构，从而实现数据去噪。与传统方法的去噪效果对比表明，本文方法可将低信噪比波形的去噪效果提高32%，将高信噪比波形的去噪效果提高6倍。同时对地磁数据的去噪结果表明，本文方法能够较完整地将地铁噪声从地磁信号波形中滤除。
    Abstract: In seismic observation, seismic data generally contain ambient noise, which reducesthe efficiency of seismic analysis. Traditional denoising methods usually need a priori knowledge of noise, and some effective data will be lost when filtering. To solve this problem, this paper proposes a seismic data denoising method based on complete ensemble empirical mode decomposition with adaptive noise （CEEMDAN） and Hurst exponent. Firstly, the signal is decomposed into a series intrinsic mode functions （IMF） by CEEMDAN method. Secondly, the Hurst exponent is used to identify the filtered IMF component. Finally, the IMF component of seismic data is reconstructed to realize data denoising. Compared with the denoising effect of traditional methods, the filtering ability of this method for low SNR waveforms is improved by 32%, and the filtering ability for high SNR waveforms is 6 times higher. At the same time, as shown in the denoising results of geomagnetic data, this method can completely filter subway noise from geomagnetic signal waveform.
    • HTML全文

  • 引言

    随着地震科技的不断发展，监测仪器的精度和广度不断提升，地震波形中包含的信号也愈加丰富。这使得一些弱震级的地震事件很容易被噪声淹没，难以提取地震信息和分析震源机制，限制了台站密度较小地区的弱震级地震分析。因此，借助数字信号处理技术和计算机技术，运用数学方法对低信噪比的地震数据进行去噪处理，从而提升信号质量，也是地震数据分析的重要的基础性工作之一。在日常地震观测中，地震记录中的背景噪声主要来自地脉动、仪器设备的自带噪声、台风、海浪潮汐等，传统的地震数据去噪方法在进行大量数据去噪时会面临两个问题，一是逐个事件进行噪声特征分析和去噪极大地增加了数据处理的工作量，二是设置统一参数进行去噪导致许多有效数据也被剔除。因此，研究一种设置简便且能够在较强噪声背景下保留波形特征的地震数据去噪方法，具有十分重要的科学意义和实用价值。

    地震数据去噪技术一直受到国内外各研究院所、专家学者的高度重视，许多不同领域的方法已经被应用到地震数据的去噪处理中，并在实际应用中取得了较好的效果。例如：f-k （频率-波数）分析法（万光南，2014；牛永效，2017）主要是利用傅里叶变换将原始波形信号从时间-空间域（t-x）转换到频率-波数域（f-k），再根据波形信号中地震数据与噪声信号的速度与频率差异，计算它们在频率-波数域的分布特征，并对噪声集中区域进行剔除，从而实现去噪；小波变换去噪技术（蔡剑华，肖晓，2015；Liu et al，2016；Lu et al，2019）则是利用小波变换将信号按照频率高低分解为不同频率的波形数据，通过去除噪声信号所在的频带，对地震数据进行重构，实现信号去噪；Ｓ变换去噪方法（陈学华等，2008；孙月，2012；Wang et al，2016）主要是同时结合傅里叶变换和小波变换的特点，通过在传统傅里叶变换的基础上加时间窗，计算地震数据与噪声信号的时间频率特征，进行构造阈值从而对地震数据去噪；基于深度学习的去噪方法（韩卫雪等，2018）利用数字图形处理、深度学习、神经网络等技术，分别计算地震数据与噪声信号的多种不同特征，利用特征参数对神经网络进行训练，优化神经网络节点，从而识别和去除噪声信号；基于模态分解技术（empirical mode decomposition，缩写为EMD）的去噪方法（杨凯，刘伟，2012；张杏莉等，2018）是利用EMD技术根据波形信号本身特点进行自适应分解，找出噪声所在本征模函数（intrinsic mode function，缩写为IMF）并予以剔除，从而实现去噪。

    上述方法在信号去噪中均取得了较好的效果，但是由于不同台站记录的噪声信号所在的频带、波数、振幅等特征存在差异，在处理不同类型事件时需要不停地调整各种特征参数才能达到较好的去噪效果。鉴于此，本文提出一种基于自适应噪声完全集合经验模态分解（complete ensemble empirical mode decomposition with adaptive noise，缩写为CEEMDAN）算法和Hurst指数（Hurst，1951）的地震数据去噪方法。该方法首先利用CEEMDAN算法的特点，根据地震数据自身频率，自适应地将地震数据分解为一系列IMF波形分量；然后，计算各IMF分量的Hurst指数，并以此作为识别地震数据和噪声信号的特征判据；最后，对地震数据所在的IMF进行重构实现去噪。

    1.   相关算法

    1.1   本文算法设计

    一般来说，一套完整的数据去噪算法主要由三套模块组成：① 波形分解模块，用于将目标数据分解成细小分量；② 成分判定模块，利用已提取出的特征参数对分量类型进行判定；③ 波形重构模块，将识别出的有效数据分量进行重构。本文在设计三个模块时重点关注了以下三点：① 由于不同类型地震事件具有不同的优势频率，简单地根据频段进行分解难以将全部有效数据分解出来；② 考虑到进行大批量数据处理时的便捷性，特征判据应能快速、有效地将地震数据与噪声信号区分开来，避免因事件类型不同需要反复调整参数的情况；③ 从现实应用角度出发，设置尽可能少的参数以确保应用更加便捷。

    鉴于此，本文采用CEEMDAN算法与Hurst指数相结合的方式进行数据去噪处理。CEEMDAN算法是在EMD算法基础上改进而来，该方法能够根据波形数据自身的频率特征，将事件按照频率高低逐步分解，从而确保数据分解的精确性和有效性。Hurst指数是一种用于描述信号长期持续性的重要指标（Zhang et al，2015），由于在地震观测中地震数据与噪声信号的持续性存在明显差异，因此使用该指数作为特征判据时不需要进行反复修改调整。图1给出了本文算法流程框图。

    图  1  本文算法流程框图
    Figure  1.  A flowchart of the method proposed in this paper
    下载: 全尺寸图片 幻灯片

    1.2   CEEMDAN算法

    由于传统的EMD分解方法存在模式混叠问题，即不同频段和长度的波形叠加共存于一段数据中，会造成分解后同一IMF分量中存在不同频率的波形混叠。该问题不仅降低了分解的效率，还降低了滤波性能。为了解决该问题并提高精度，本文采用由Torres等（2011）提出的CEEMDAN方法。CEEMDAN方法的计算过程如下：

    计算IMF1分量。在原始波形信号x（t）中分别加入正负成对的高斯白噪声$E_1 （ n^{ （ i ） } ） $ （i＝1，2，···，N）构成信号集合{x（t）＋E1（n（i））}，利用EMD分别对每一个信号进行分解，用分解得到的第一个IMF分量组成集合{$h_1^{ （ i ） }$}，对该集合求平均得到IMF1的分量h1 ［ 式（1） ］ ，并计算IMF1的残余r1 ［ 式（2） ］ 。

    $$ {h_1} ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^N {h_1^{ （ i ） }} $$ (1)
    $$ {r_1} ＝ x （ t ） － {h_1} $$ (2)

    同理计算IMF2分量，得到IMF2分量h2，并计算残余r2。

    $$ {h_2} ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^N {h_2^{ （ i ） }} \text{，} $$ (3)
    $$ {r_2} ＝ {r_1} － {h_2} {\text{.}} $$ (4)

    依次类推，可计算得到原始信号的IMFm分量hm和残余rm分别为

    $$ {h_m} ＝ \frac{1}{N}\sum\limits_{i ＝ 1}^N {h_m^{ （ i ） }} \text{，} $$ (5)
    $$ {r_m} ＝ {r_{m － 1}} － {h_m} {\text{.}} $$ (6)

    重复上述步骤，直到残余信号为单调函数，完成分解。此时原始信号x（t）的分解结果为

    $$ x （ t ） ＝ \sum\limits_{j ＝ 1}^m {{h_j}} ＋ {r_m} {\text{.}} $$ (7)

    1.3   Hurst指数

    本文使用聚合方差法计算Hurst指数。具体步骤为：对于原始信号序列x（t），t＝1，2，···，N，用长度为$ M $的时间窗，将x（t）划分为Xk（t）（k＝1，2，···，N/M）个区间，分别计算每个区间$ X_k （ t ） $的平均值。

    $$ {\overline X_k} （ t ） ＝ \frac{1}{M}\sum\limits_{i ＝ 1}^M {{X_i}} \qquad k ＝ 1， 2， \cdots， \frac{N}{M} \text{，} $$ (8)

    式中N/M不为整数时向上取整，各区间相互不重叠，最后一个时间窗的长度以实际的数据量为准。

    计算各区间$ X_k （ t ） $平均值的样本方差，即

    $$ {\rm{Va}}{{\rm{r}}_M （ t ） } ＝ \frac{1}{{N/M}}\sum\limits_{k ＝ 1}^{N/M} {{{[{{\overline X}_k} （ t ） － \overline X]}^2}}{\text{.}} $$ (9)

    分别计算M＝1，2，···，N/4时对应的${\rm{Var}}_M （ t ） $，并在双对数坐标系上用最小二乘法拟合$ ［ M， {\rm{Var}}_M （ t ） ］ $，即

    $$ \lg ［ {\rm{Var}}_M （ t ） ］ ＝ A\lg M ＋ b ，$$ (10)

    拟合后直线的斜率A即为Hurst指数$ h $。

    2.   波形去噪

    2.1   基于CEEMDAN的信号分解

    为了验证本文算法的有效性，从近年来广西地震台的地震记录中挑选四种不同类型且背景噪声较大的事件波形进行去噪处理，事件具体信息列于表1。四个事件的波形均由宽频带地震计记录，采样率为100 sps，事件长度为120 s。本文选择垂直向波形进行分析，图2给出了四个事件的垂直向波形。从图中可以看出，由于几个事件的震级小、距离远，而背景噪声又比较强，事件的震相较难识别。

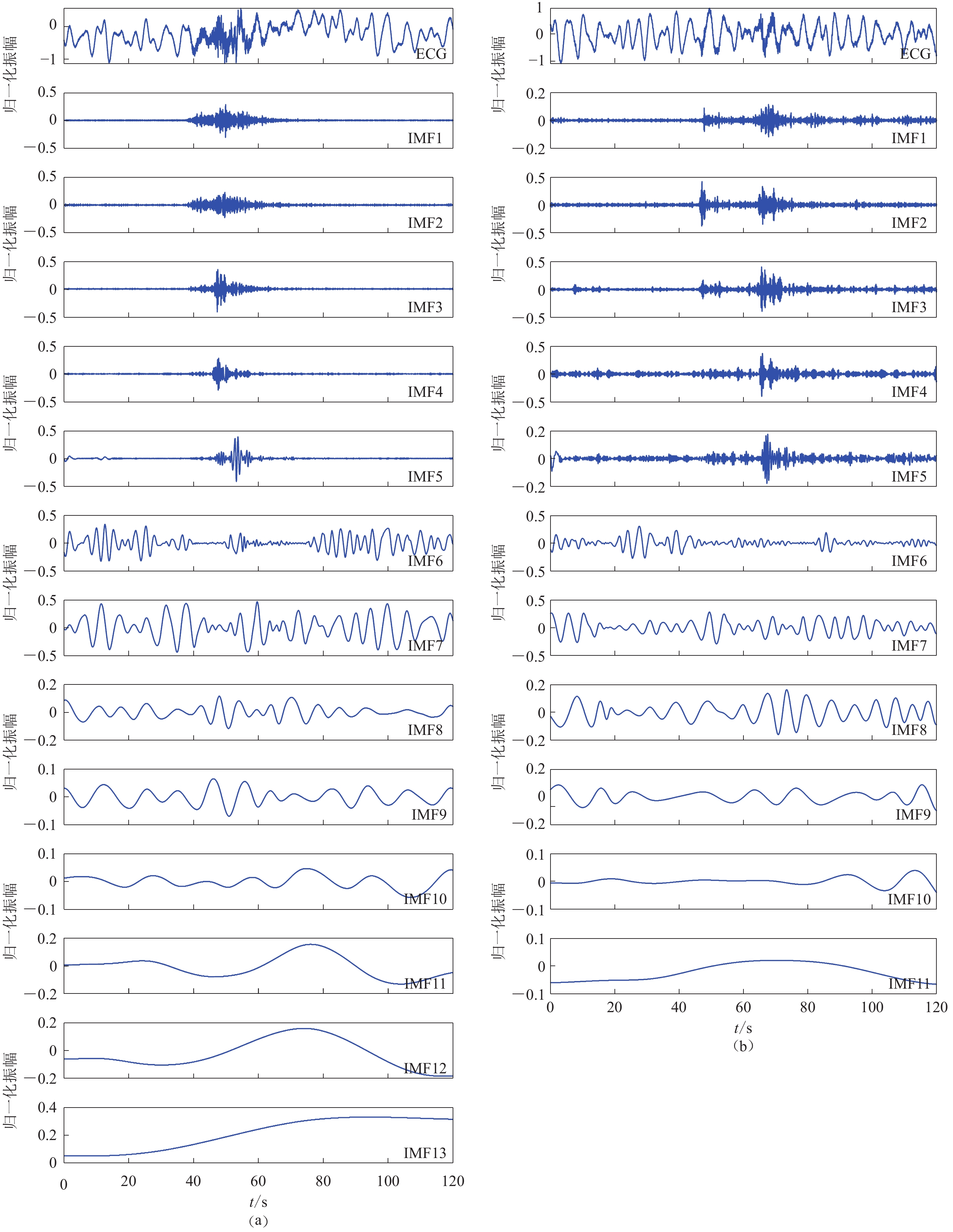
    表  1  本文所选事件的信息
    Table  1.  The information of events selected in this paper
    事件序号事件类型发震日期震中位置记录台站震中距/kmML
    a天然地震2021-04-28广西百色FUN731.3
    b天然地震 2017-11-25广西灵川YOF1481.9
    c人工爆破 2021-04-04广西南宁DAQ882.0
    d山体坍塌2020-06-23广西桂林GUL362.3
    下载: 导出CSV 
    | 显示表格
    图  2  事件垂直向原始波形
    Figure  2.  Vertical original waveforms of the events
    下载: 全尺寸图片 幻灯片

    在使用CEEMDAN算法时，为了避免添加过高的噪声对原始信号产生干扰，且过大的运算量会导致运行时间过长，将CEEMDAN算法的附加噪声振幅定为0.01，最大筛选迭代次数设为300。图3给出了四个事件的CEEMDAN分解结果，可以看出，地震波形主要集中在IMF1−IMF5，其余的则是背景噪声信号。

    图  3  CEEMDAN算法分解结果
    （a） 百色地震事件波形；（b） 灵川地震事件波形
    Figure  3.  Decomposition results of CEEMDAN
    （a） Baise earthquake waveform；（b） Lingchuan earthquake waveform
    下载: 全尺寸图片 幻灯片
    图  3  CEEMDAN算法分解结果
    （c） 南宁爆破事件波形；（d） 桂林坍塌事件波形
    Figure  3.  Decomposition results of CEEMDAN
    （c） Nanning blasting waveform；（d） Guilin collapse waveform
    下载: 全尺寸图片 幻灯片

    2.2   基于Hurst指数的IMF选择

    Hurst指数作为一种用于描绘时间序列波形长期记忆性的重要参数，可以反映事件波形震动的持续性特征。根据式（10）计算得到的$ h $值在表示波形的持续性方面具有以下特征：① 当h＝0.5时，说明该波形具有随机性，表现出随机震动；② 当h＜0.5时，说明该波形具有反持续性；③ 当h＞0.5时，说明该波形具有长期记忆性。

    在日常的地震监测中可以发现，地震记录的背景噪声是持续存在的，且占据了大部分的波形记录，表现出长期记忆性，而地震波相较于背景噪声则具有频域丰富、持续时间短的特点。因此，Hurst指数可以作为检验分解后的IMF分量是否为地震数据的重要指标。

    根据Hurst指数的定义，本文将h＜0.5的分量作为地震数据的IMF分量，将h≥0.5的分量作为噪声IMF分量。表2给出了四个事件IMF分量Hurst指数的计算结果。根据Hurst指数不同，将h＜0.5的IMF分量作为地震数据进行重构。图4展示了四个事件的去噪效果。结果表明，利用本文方法去噪后，波形震相更加清晰且保留了波形特征。

    表  2  表1中四个事件的IMF分量的Hurst指数
    Table  2.  The Hurst exponents of different IMF components for four events in Table 1
    分量序号事件a事件b事件c事件d
    IMF10.302 50.294 60.258 90.359 4
    IMF20.322 60.407 50.425 50.325 4
    IMF30.307 00.287 50.356 10.466 3
    IMF40.418 90.333 70.306 30.487 1
    IMF50.483 80.384 60.515 90.361 1
    IMF60.655 80.640 80.612 20.647 8
    IMF70.686 00.686 20.658 90.683 1
    IMF80.763 80.792 90.796 60.653 0
    IMF90.806 20.877 70.870 90.864 5
    IMF100.969 30.916 50.992 90.908 0
    IMF110.973 30.966 81.007 00.955 1
    IMF120.985 11.009 21.004 0
    IMF130.994 9
    下载: 导出CSV 
    | 显示表格
    图  4  使用本文方法所得四个事件的去噪结果
    左侧为原始波形，右侧为去噪后波形。（a） 百色地震波形；（b） 灵川地震波形；（c） 南宁爆破事件波形；（d） 桂林坍塌事件波形
    Figure  4.  Denoising results of the four events by the method proposed in this paper
    The left column stands for original waveforms and the right column stands for denoising waveforms. （a） Baise earthquake waveform；（b） Lingchuan earthquake waveform；（c） Nanning blasting waveform；（d） Guilin collapse waveform
    下载: 全尺寸图片 幻灯片

    3.   去噪效果分析

    为了验证本文去噪方法的有效性，将文本方法结果与传统的带通滤波器、小波包变换及EMD等去噪方法进行对比分析。

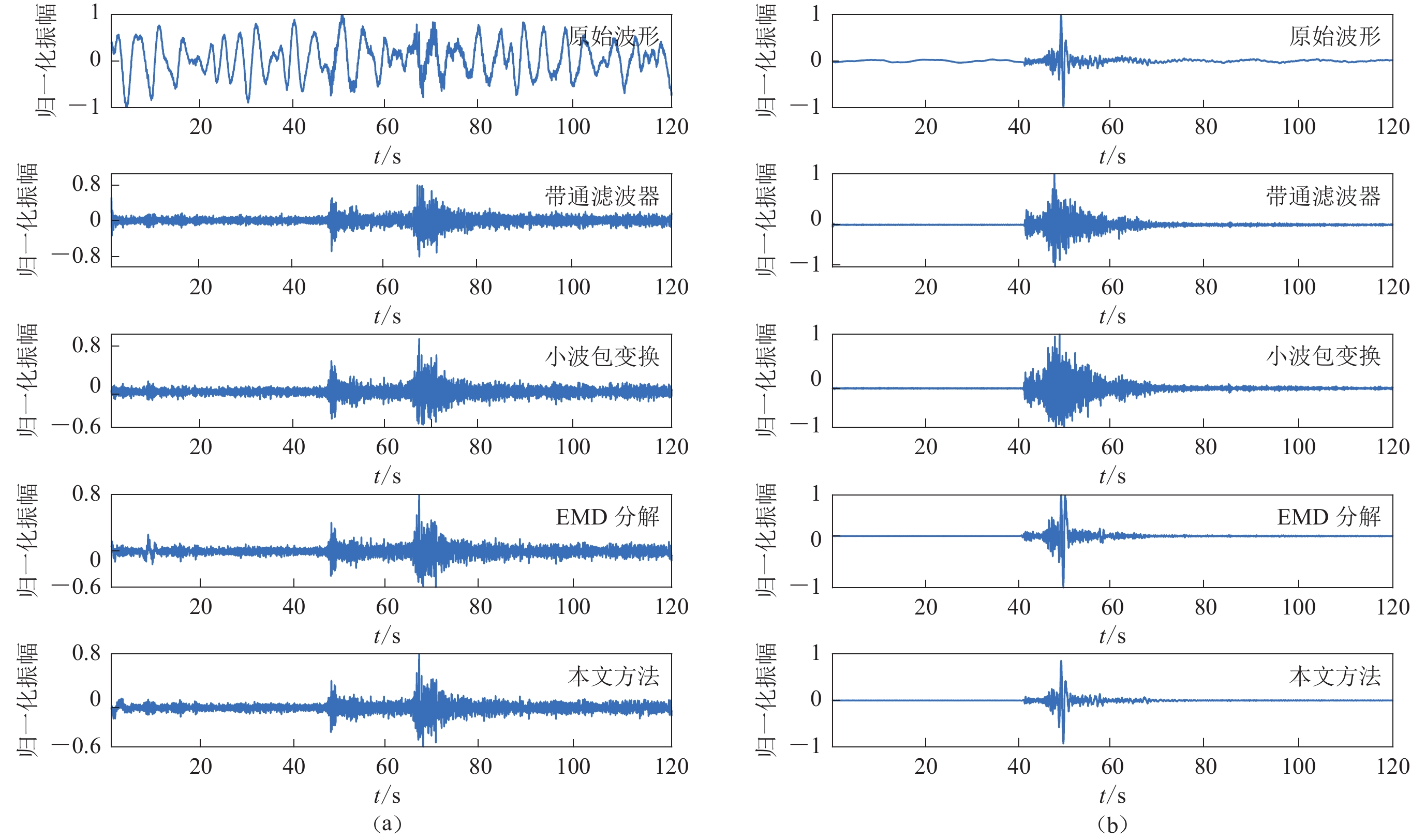
    图5为使用上述三种方法及本文方法分别对灵川地震事件和桂林坍塌事件进行去噪后的结果，其中带通滤波器去噪方法采用的是巴特沃斯（Butterworth）带通滤波器，小波包变换去噪方法采用db4基函数进行四层分解去噪。从图5可以看出：虽然传统的方法能够较好地滤除背景噪声，但是在去噪的同时也会降低该频段地震数据（如短周期面波）滤除，导致地震波产生变形；而本文的方法在去除噪声的同时，还能够较好地保存地震数据不同频段的波形特征。

    图  5  不同方法对灵川地震事件（a）和桂林坍塌事件（b）的去噪结果
    Figure  5.  Denoising results of Lingchuan earthquake （a） and Guilin collapse （b） by different methods
    下载: 全尺寸图片 幻灯片

    为了能够对几种方法的去噪效果进行量化评价，本文采用质量因子Q值（Chen，Sacchi，2015）和均方根误差（RMSE）作为评价去噪效果优劣的指标。

    $$ Q ＝ 10\sqrt {\lg \frac{{\displaystyle\sum\limits_{i ＝ 1}^n {s_{\rm{o}}^2 （ i ） } }}{{\displaystyle\sum\limits_{i ＝ 1}^n {{{[{s_{\rm{o}}} （ i ） － {s_{\rm{d}}} （ i ） ]}^2}} }}} \text{，} $$ (11)
    $$ {\rm{RMSE}} ＝ \sqrt {\frac{1}{n}\sum\limits_{i ＝ 1}^n {[{s_{\rm{o}}} （ i ） － } {s_{\rm{d}}} （ i ） {]^2}} \text{，} $$ (12)

    式中，so（i）为原始波形信号，sd（i）为去噪后的波形信号。Q值越高而RMSE越低，说明去噪的效果越好。表3给出了上述三种方法与本文方法去噪效果的质量因子Q值，可见：与带通滤波器和小波包变换等传统去噪方法相比，对于低信噪比的波形（表1事件b），本文方法的Q值比传统方法Q值高32%，而RMSE降低3%；对于高信噪比的波形（表1事件d），本文方法的Q值则高出648.3%，而RMSE降低33%。这表明相对于传统方法，本文方法的去噪性能更好。

    表  3  不同去噪方法的质量因子Q值和均方根误差RMSE
    Table  3.  Quality factor Q and root-mean-square error RMSE of different denoising methods
    去噪方法灵川地震事件桂林坍塌事件
    Q值RMSEQ值RMSE
    带通滤波器 0.723 9 0.380 1 1.360 1 0.076 1
    小波包变换 0.718 5 0.375 6 1.193 9 0.073 3
    EMD方法 0.854 9 0.374 7 7.344 2 0.040 0
    本文方法 0.955 9 0.373 9 9.606 9 0.025 7
    下载: 导出CSV 
    | 显示表格

    4.   本文方法在地磁观测数据去噪中的应用

    近年来，随着城市的快速扩张，特别是高铁、地铁、高压输电线路、高速公路的扩建，各地的地磁观测数据无可避免地经常受到各种类型的外加干扰，导致记录的数据量暴增，而有效信号的比率却不断下降，这对震前地磁异常特征提取的研究造成了较为严重的干扰。因此，地磁观测数据的去噪研究具有非常重要的意义。

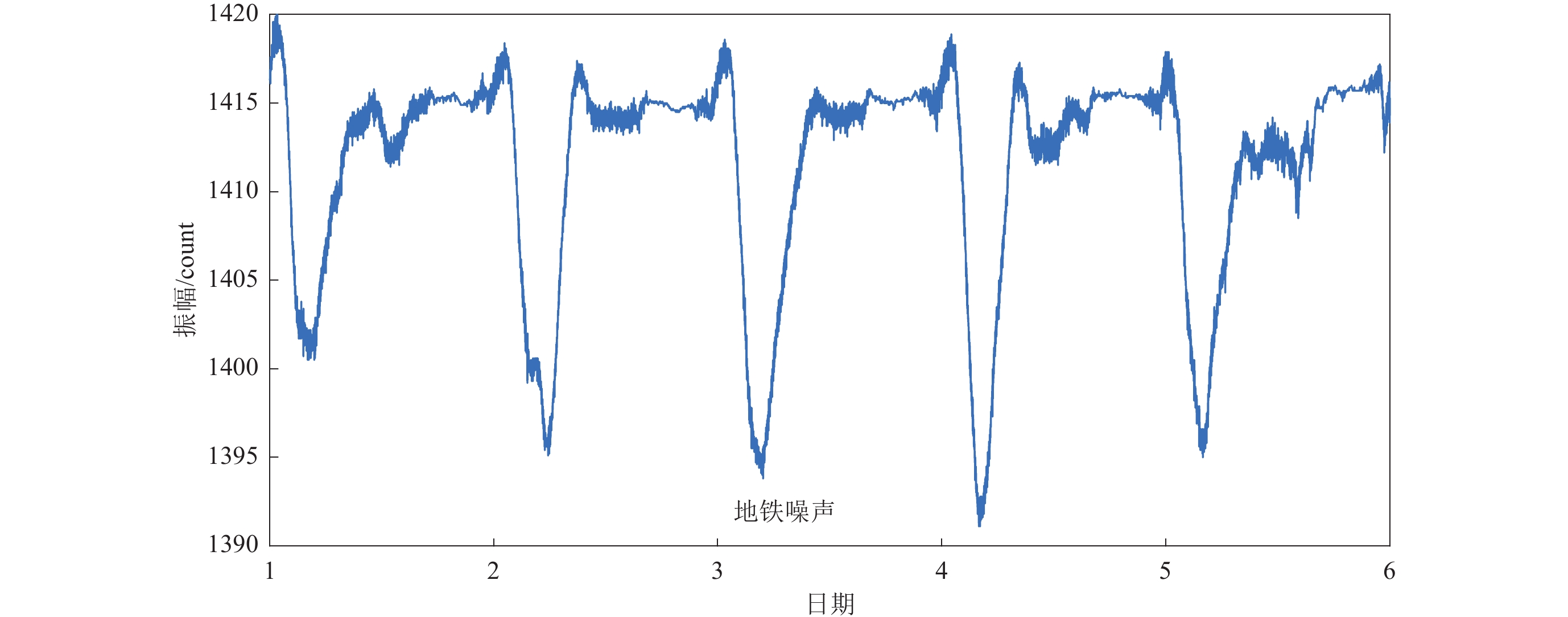
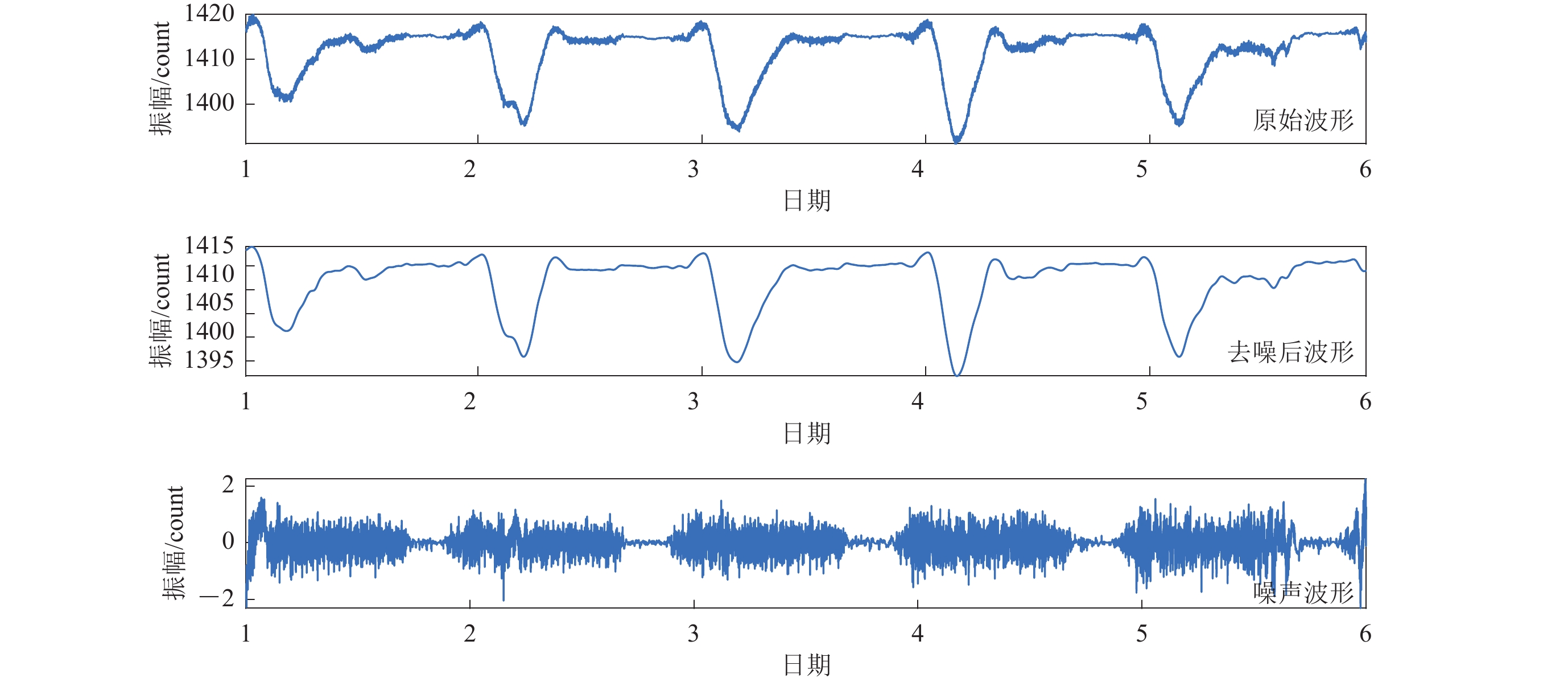
    由于定点地磁观测与地震观测都具有长期性、连续性的特征，因此，本文的方法同样可以应用于地磁观测数据的噪声去除。图6给出了邕宁地磁台2021年1月1日00时至2021年1月5日24时Z分向的地磁原始观测数据（分钟值）。可以看出，由于受到地铁干扰，波形中出现了大量高频噪声。

    图  6  邕宁地磁台2021年1月1日0时至5日24时观测数据波形
    Figure  6.  Observation waveform at Yongning geomagnetic station from 00:00 on January 1 to 24:00 on January 5，2021
    下载: 全尺寸图片 幻灯片

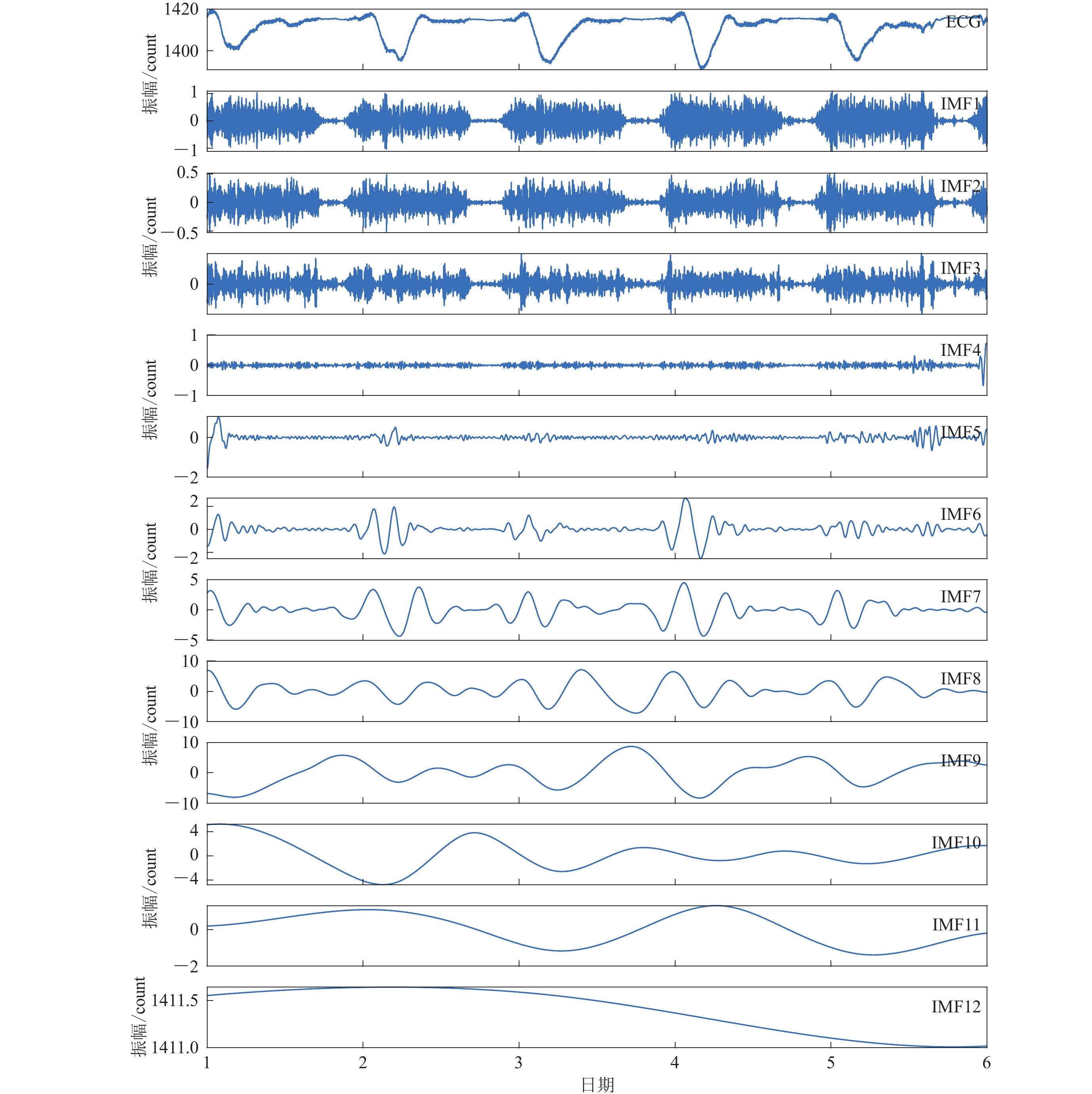
    图7和表4给出了使用本文方法对该段数据进行分解的结果以及各IMF分量的Hurst指数。可以看出，地铁的噪声信号主要集中在IMF1−IMF5分量，而IMF6之后的分量是地磁每日周期性变化数据。

    图  7  地磁数据CEEMDAN分解结果
    Figure  7.  Decomposition results of geomagnetic data by CEEMDAN
    下载: 全尺寸图片 幻灯片
    表  4  地磁数据IMF分量的Hurst指数
    Table  4.  The Hurst exponent of different IMFs from geomagnetic data
    序号Hurst指数序号Hurst指数序号Hurst指数
    IMF1 0.284 6 IMF5 0.497 9 IMF9 0.954 7
    IMF2 0.323 2 IMF6 0.583 0 IMF10 0.989 9
    IMF3 0.208 0 IMF7 0.702 9 IMF11 0.997 1
    IMF4 0.352 4 IMF8 0.861 3 IMF12 1.006 3
    下载: 导出CSV 
    | 显示表格

    地磁观测与地震观测不同，地磁观测主要是记录磁场的长期变化规律，而短时的干扰则是需要去除的噪声信号。因此，使用Hurst指数作为判据时，类型选择与地震数据相反，h＞0.5的分量是有效信号，而h≤0.5的分量则作为噪声信号。图8给出了去噪后的地磁波形和噪声波形，通过与原始波形的对比可以看出，地磁数据波形的周期性变化得到较完好的保留。由此可以得出，本文的方法在应用于地磁数据去噪时，可以有效地去除噪声数据，并能够较好地保留波形的变化特征。

    图  8  地磁数据去噪结果
    Figure  8.  Denoising results of geomagnetic data
    下载: 全尺寸图片 幻灯片

    5.   讨论与结论

    本文提出了一种基于CEEMDAN算法和hurst指数的地震信号去噪方法，该方法已在不同类型地震波形上进行了测试。相较于传统方法，本文方法对于低信噪比波形和高信噪比波形的去噪性能分别提高了33%和6倍。同时，本文方法能够根据信号数据自身频率和振幅变化的特点，自适应地进行噪声信号识别。这意味着在处理大量地震数据时，不再需要逐类型事件分析噪声特征，这将有效减少分析人员处理数据的工作量。而对于地磁信号的滤波结果表明，本文的方法同样能够较为完整地将地铁噪声从地磁数据中识别滤除。在未来的工作中，我们将收集更多类型的地震数据和地磁数据进行验证，同时还将把该方法推广应用于连续重力和形变等观测数据的噪声处理研究中。

  • 图  1   本文算法流程框图

    Figure  1.   A flowchart of the method proposed in this paper

    下载: 全尺寸图片 幻灯片

    图  2   事件垂直向原始波形

    Figure  2.   Vertical original waveforms of the events

    下载: 全尺寸图片 幻灯片

    图  3   CEEMDAN算法分解结果

    （a） 百色地震事件波形；（b） 灵川地震事件波形

    Figure  3.   Decomposition results of CEEMDAN

    （a） Baise earthquake waveform；（b） Lingchuan earthquake waveform

    下载: 全尺寸图片 幻灯片

    图  3   CEEMDAN算法分解结果

    （c） 南宁爆破事件波形；（d） 桂林坍塌事件波形

    Figure  3.   Decomposition results of CEEMDAN

    （c） Nanning blasting waveform；（d） Guilin collapse waveform

    下载: 全尺寸图片 幻灯片

    图  4   使用本文方法所得四个事件的去噪结果

    左侧为原始波形，右侧为去噪后波形。（a） 百色地震波形；（b） 灵川地震波形；（c） 南宁爆破事件波形；（d） 桂林坍塌事件波形

    Figure  4.   Denoising results of the four events by the method proposed in this paper

    The left column stands for original waveforms and the right column stands for denoising waveforms. （a） Baise earthquake waveform；（b） Lingchuan earthquake waveform；（c） Nanning blasting waveform；（d） Guilin collapse waveform

    下载: 全尺寸图片 幻灯片

    图  5   不同方法对灵川地震事件（a）和桂林坍塌事件（b）的去噪结果

    Figure  5.   Denoising results of Lingchuan earthquake （a） and Guilin collapse （b） by different methods

    下载: 全尺寸图片 幻灯片

    图  6   邕宁地磁台2021年1月1日0时至5日24时观测数据波形

    Figure  6.   Observation waveform at Yongning geomagnetic station from 00:00 on January 1 to 24:00 on January 5，2021

    下载: 全尺寸图片 幻灯片

    图  7   地磁数据CEEMDAN分解结果

    Figure  7.   Decomposition results of geomagnetic data by CEEMDAN

    下载: 全尺寸图片 幻灯片

    图  8   地磁数据去噪结果

    Figure  8.   Denoising results of geomagnetic data

    下载: 全尺寸图片 幻灯片

    表  1   本文所选事件的信息

    Table  1   The information of events selected in this paper

    事件序号事件类型发震日期震中位置记录台站震中距/kmML
    a天然地震2021-04-28广西百色FUN731.3
    b天然地震 2017-11-25广西灵川YOF1481.9
    c人工爆破 2021-04-04广西南宁DAQ882.0
    d山体坍塌2020-06-23广西桂林GUL362.3
    下载: 导出CSV

    表  2   表1中四个事件的IMF分量的Hurst指数

    Table  2   The Hurst exponents of different IMF components for four events in Table 1

    分量序号事件a事件b事件c事件d
    IMF10.302 50.294 60.258 90.359 4
    IMF20.322 60.407 50.425 50.325 4
    IMF30.307 00.287 50.356 10.466 3
    IMF40.418 90.333 70.306 30.487 1
    IMF50.483 80.384 60.515 90.361 1
    IMF60.655 80.640 80.612 20.647 8
    IMF70.686 00.686 20.658 90.683 1
    IMF80.763 80.792 90.796 60.653 0
    IMF90.806 20.877 70.870 90.864 5
    IMF100.969 30.916 50.992 90.908 0
    IMF110.973 30.966 81.007 00.955 1
    IMF120.985 11.009 21.004 0
    IMF130.994 9
    下载: 导出CSV

    表  3   不同去噪方法的质量因子Q值和均方根误差RMSE

    Table  3   Quality factor Q and root-mean-square error RMSE of different denoising methods

    去噪方法灵川地震事件桂林坍塌事件
    Q值RMSEQ值RMSE
    带通滤波器 0.723 9 0.380 1 1.360 1 0.076 1
    小波包变换 0.718 5 0.375 6 1.193 9 0.073 3
    EMD方法 0.854 9 0.374 7 7.344 2 0.040 0
    本文方法 0.955 9 0.373 9 9.606 9 0.025 7
    下载: 导出CSV

    表  4   地磁数据IMF分量的Hurst指数

    Table  4   The Hurst exponent of different IMFs from geomagnetic data

    序号Hurst指数序号Hurst指数序号Hurst指数
    IMF1 0.284 6 IMF5 0.497 9 IMF9 0.954 7
    IMF2 0.323 2 IMF6 0.583 0 IMF10 0.989 9
    IMF3 0.208 0 IMF7 0.702 9 IMF11 0.997 1
    IMF4 0.352 4 IMF8 0.861 3 IMF12 1.006 3
    下载: 导出CSV
    • 参考文献(23)
  • 蔡剑华,肖晓. 2015. 基于小波自适应阈值去噪的MT信号处理方法[J]. 地球物理学进展,30(6):2433–2439. doi: 10.6038/pg20150601

    Cai J H,Xiao X. 2015. Method of processing magnetotelluric signal based on the adaptive threshold wavelet[J]. Progress in Geophysics,30(6):2433–2439 (in Chinese).
    陈学华,贺振华,黄德济. 2008. 广义S变换及其时频滤波[J]. 信号处理,24(1):28–31. doi: 10.3969/j.issn.1003-0530.2008.01.007

    Chen X H,He Z H,Huang D J. 2008. Generalized S transform and its time-frequency filtering[J]. Signal Processing,24(1):28–31 (in Chinese).
    韩卫雪,周亚同,池越. 2018. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探,57(6):862–869. doi: 10.3969/j.issn.1000-1441.2018.06.008

    Han W X,Zhou Y T,Chi Y. 2018. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum,57(6):862–869 (in Chinese).
    牛永效. 2017. 基于频率及f-k域联合应用的地震波去噪技术研究[J]. 铁道标准设计,61(2):47–49.

    Niu Y X. 2017. Research on seismic data noise reduction based on combined application of frequency and f-k domain filter[J]. Railway Standard Design,61(2):47–49 (in Chinese).
    孙月. 2012. 基于广义S变换和阈值函数的地震信号去噪研究[D]. 长春: 吉林大学: 19–26.

    Sun Y. 2012. Seismic Signal Denoising Research Based on Generalized S Transformation and Threshold Function[D]. Changchun: Jilin University: 19–26 （in Chinese）.
    万光南. 2014. f-k滤波在压制面波噪声中的应用[J]. 中州煤炭,(2):99–101.

    Wan G N. 2014. Application of f-k filtering in noise suppression of surface wave[J]. Zhongzhou Coal,(2):99–101 (in Chinese).
    杨凯,刘伟. 2012. 基于改进EMD的地震信号去噪[J]. 西南石油大学学报(自然科学版),34(4):75–82.

    Yang K,Liu W. 2012. Random noise attenuation of seismic signal based on improved EMD[J]. Journal of Southwest Petroleum University (Science &Technology Edition),34(4):75–82 (in Chinese).
    张杏莉,卢新明,贾瑞生,阚淑婷. 2018. 基于变分模态分解及能量熵的微震信号降噪方法[J]. 煤炭学报,43(2):356–363. doi: 10.13225/j.cnki.jccs.2017.4153

    Zhang X L,Lu X M,Jia R S,Kan S T. 2018. Micro-seismic signal denoising method based on variational mode decomposition and energy entropy[J]. Journal of China Coal Society,43(2):356–363 (in Chinese).

    Chen K,Sacchi M D. 2015. Robust reduced-rank filtering for erratic seismic noise attenuation[J]. Geophysics,80(1):V1–V11.

    Hurst H E. 1951. Long-term storage capacity of reservoirs[J]. Trans Am Soc Civ Eng,116(1):770–799. doi: 10.1061/TACEAT.0006518

    Liu W,Cao S Y,Chen Y K. 2016. Seismic time-frequency analysis via empirical wavelet transform[J]. IEEE Geosci Remote Sens Lett,13(1):28–32. doi: 10.1109/LGRS.2015.2493198

    Lu Y,Huang Y M,Xue W,Zhang G B. 2019. Seismic data processing method based on wavelet transform for denoising[J]. Cluster Comput,22(3):6609–6620.

    Torres M E, Colominas M A, Schlotthauer G, Flandrin P. 2011. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing （ICASSP）. Prague: IEEE: 4144–4147.

    Wang Y Q, Peng Z M, He Y M. 2016. Time-frequency representation for seismic data using sparse S transform[C]//2016 2nd IEEE International Conference on Computer and Communications （ICCC）. Chengdu: IEEE: 1923–1926.

    Zhang C,Li Y,Lin H B,Yang B J. 2015. Signal preserving and seismic random noise attenuation by Hurst exponent based time-frequency peak filtering[J]. Geophys J Int,203(2):901–909. doi: 10.1093/gji/ggv340
    • 相关文章
    • 施引文献(8)

  • 期刊类型引用(5)

    1. 刘引鸽，罗紫薇，郭慧君，李丹丹，林茂琦，吕欣怡. 基于遥感数据的河谷地区气候水文变化特征及区域差异——以宝鸡地区为例. 水土保持研究. 2025(01): 181-194 . 百度学术
    2. 胡萍，廉哲. 改进粒计算算法下时序数据关联规则挖掘仿真. 计算机仿真. 2024(03): 448-452 . 百度学术
    3. 李汝嘉，贺壹婷，季荣彪，李亚东，孙晓海，陈娇娇，吴叶辉，王灿宇. 基于量子行为花朵授粉算法优化LSTM模型. 吉林大学学报(理学版). 2024(05): 1163-1178 . 百度学术
    4. 丁晓红，蒋雪峰. 通道奇异谱分析的绿色建筑能耗预测方法仿真. 计算机仿真. 2024(09): 351-355 . 百度学术
    5. 马迪迪，赵静，林亚龙，王婧雯. 一种轨旁设备可靠性度量方法的设计与实现. 环境技术. 2023(12): 24-30 . 百度学术

    其他类型引用(3)

    • 资源附件(0)
图(9)  /  表(4)
计量
  • 文章访问数:  390
  • HTML全文浏览量:  196
  • PDF下载量:  107
  • 被引次数: 8
出版历程
  • 收稿日期:  2021-10-25
  • 修回日期:  2022-03-24
  • 网络出版日期:  2022-12-12
  • 发布日期:  2023-03-14

目录

摘要
HTML全文

  • 引言

  • 1.   相关算法

  • 1.1   本文算法设计

  • 1.2   CEEMDAN算法

  • 1.3   Hurst指数

  • 2.   波形去噪

  • 2.1   基于CEEMDAN的信号分解

  • 2.2   基于Hurst指数的IMF选择

  • 3.   去噪效果分析

  • 4.   本文方法在地磁观测数据去噪中的应用

  • 5.   讨论与结论

参考文献(23)
相关文章
施引文献
资源附件(0)

/

返回文章
返回

本系统由 北京仁和汇智信息技术有限公司 开发  技术支持：info@rhhz.net 百度统计