Joint inversion of multi-station receiver functions and gravity data for imaging Moho variations and average crustal vP/vS ratios
-
摘要: 地壳厚度和波速比是研究地壳结构和组分的两个重要参数,可为区域构造研究提供重要约束。接收函数被广泛地用于确定地壳厚度和波速比,例如H-κ方法或H-κ-c方法,但是该方法只能确定台站下方的地壳厚度和速度比,当地震台站分布稀疏时,很难约束台站间的横向不均匀性。另一方面,重力数据也可用于莫霍面的起伏变化研究,它在横向上覆盖很好,有较高的分辨率,但在纵向上分辨率相对较低。为此,本研究提出了一种联合反演算法求解莫霍面深度和地壳波速比参数。联合反演算法综合考虑了接收函数在纵向上的较高分辨率和重力数据在横向上的较高分辨率,同时拟合区域内所有台站上的接收函数和区域重力数据。模型测试表明联合反演算法较单一的接收函数反演更精确,特别是对于地壳厚度的确定。Abstract: Crustal thickness and vP/vS ratio are two important parameters for understanding crustal structure and composition, which can help to study regional tectonics. Receiver function analysis has been widely used for determining crustal thickness and vP/vS ratio by the H-κ method or the H-κ-c method. However, it can only acquire average crustal thickness and vP/vS ratio beneath each seismic station, but cannot constrain their lateral variations among seisimic stations due to their sparse and irregular distribution. On the other hand, the gravity data has been widely used to derive the Moho variaitons, which has a good coverage and resolution laterally but poor resolution vertically. Therefore, in this study we have developed a new joint inversion method of receiver functions and gravity data to simultaneously invert for variations of Moho depths and average crustal vP/vS ratios in a region. The method takes advantage of complementary strengths of receiver functions and gravity data, and can simultaneously fit all receiver functions and gravity data in the region. The synthetic tests show that the proposed joint inversion method produces more reliable results than only receiver function analysis, especially for the crustal thickness.
-
Keywords:
- joint inversion /
- receiver function /
- gravity /
- Moho /
- vP/vS ratio
-
引言
对于区域构造研究来说,地壳厚度和波速比vP/vS是两个重要参数,可以用于揭示地壳属性和约束深部动力学过程(Owens,Zandt,1997;Tian,Zhang,2013)。自二十世纪七十年代以来,远震接收函数被广泛地用于研究地壳和地幔中的界面,如莫霍面、410 km和660 km界面。Zhu和Kanamori (2000)提出了H-κ叠加法获取台站下方的地壳厚度和速度比,该方法利用远震P波在莫霍面附近产生的Ps转换波和多次反射波,通过赋予不同类型的波一定的权重进行网格搜索,获取最佳的地壳厚度和速度比。由于该方法简洁且不需要人工挑选到时,近年来已经得到广泛的应用(Julià,Mejía,2004;Niu et al,2007;He et al,2014;Li et al,2014;宋婷等,2020)。
H-κ叠加法获取的是台站下方一定范围内综合的地壳厚度和速度比,然而当地震台站下方存在沉积层或者较大的各向异性介质差异时,很难获取比较准确的结果。为此,张洪双等(2009)发展了H-κ-θ估算倾斜地区的莫霍面和地壳波速比;Tao等 (2014)提出了H-β方法,该方法通过地震波场延拓来分离浅部沉积层多次波的干扰来获取更精确的地壳厚度和速度比;Li等(2019)提出了H-κ-c方法来校正台站下方地壳物质不均一和莫霍面倾斜带来的影响。然而由于地震台站分布稀疏且不规则,当利用单个台站反演结果进行内插时,忽略了地壳的横向不均一性,对台站间的横向变化缺乏约束。
重力数据近年来已经被广泛地用于研究莫霍面结构(Silva et al,2006;Aitken,2010;郭良辉等,2012;Aitken et al,2013;Feng et al,2014)。相对于地震数据而言,重力异常数据对地下结构的约束随着深度的递增而快速衰减,因此在纵向上的分辨率相对较低。但重力数据在横向上有较好的分辨率,同时重力数据一般分布得比较规则,尤其是卫星重力数据。
基于接收函数与重力数据二者之间的互补性,可以通过联合反演更好地约束地壳厚度和波速比。联合反演的优势在于综合不同地球物理数据对地下结构的互补性,进而减少单一数据反演的不确定性,从而获取更加准确的地下结构。例如,通过重力和地震体波走时数据的联合反演可以获取更加可靠的地下三维速度或密度结构(Maceira,Ammon,2009;Chai et al,2015;Syracuse et al,2016,2017;Zhao et al,2020)。为了减少台站下方求解地壳厚度和速度比的不确定性,一些学者引入重力数据进行额外约束(Lowry,Pérez-Gussinyé,2011;Shi et al,2018;Guo et al,2019)。在他们的研究中,利用最大似然概率函数构建重力数据与地壳参数(包含地壳厚度和波速比)的关系,而后对初始H-κ叠加方法获取的结果引入重力似然函数的约束,获取单台下方更加精确的地壳参数。但该方法的结果相对依赖于初始的H-κ结果,引入的重力似然函数仅约束单个台站,缺乏对台站间地壳参数横向变化的约束。
鉴于此,本研究拟提出一种新的接收函数和重力联合反演算法,反演研究区域的莫霍面起伏和地壳平均波速比变化。与现有的接收函数和重力联合反演算法(Lowry,Pérez-Gussinyé,2011;Shi et al,2018;Guo et al,2019)相比,本文方法是利用区域内所有台站的接收函数和重力数据,同时确定区域内莫霍面的起伏和地壳平均波速比,而不是仅确定单个台站下方的地壳参数。本文联合反演方法更有效地考虑了接收函数在纵向上较高的分辨率和重力数据在横向上较高的分辨率,同时拟合接收函数和重力数据。最后通过分别构建简单和复杂地壳模型进行测试,以验证本文联合反演算法的准确性。
1. 方法
对于接收函数和重力联合反演,首先分别介绍接收函数单独反演地壳参数和密度界面正演算法,然后介绍新提出的接收函数和重力联合反演方法。
1.1 接收函数
远震P波在经过台站下方的莫霍面时,由于波阻抗差的存在会产生转换波。接收函数包含直达P波、莫霍面的转换波Ps,以及多次反射波(主要包括PpPs和PsPs+PpSs)。其中,三个震相与初至P波的到时差可以表示为(Zhu,Kanamori,2000)
$$ {t}_{{\rm{Ps}}}=H\left(\sqrt{{\left(\frac{\kappa }{{\nu }_{{\rm{P}}}}\right)}^{2}-{p}^{2}}-\sqrt{\frac{1}{{\nu }_{{\rm{P}}}^{2}}-{p}^{2}}\right),$$ (1) $$ {t}_{{{\rm{Pp}}}{{\rm{Ps}}}}=H\left(\sqrt{{\left(\frac{\kappa }{{\nu }_{{\rm{P}}}}\right)}^{2}-{p}^{2}}+\sqrt{\frac{1}{{\nu }_{{\rm{P}}}^{2}}-{p}^{2}}\right),$$ (2) $$ {t}_{{{\rm{PsPs}}+{{\rm{PpSs}}}}}=H\left(2\sqrt{{\left(\frac{\kappa }{{\nu }_{{\rm{P}}}}\right)}^{2}-{p}^{2}}\right), $$ (3) 式中,${t}_{{{\rm{P}}}_{{\rm{S}}}}$,${t}_{{{\rm{PpPs}}}}$和${t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}$分别为转换波和多次波相对于直达P波的到时差,H为地壳厚度(其中$H={H}_{{\rm{Moho}}}+{H}_{{\rm{topo}}}$,HMoho为台站下方的莫霍面起伏,${H}_{{\rm{topo}}}$为台站相对于平均海平面的地形起伏),κ=vP/vS,p为射线参数。H-κ方法假定vP为定值(Zhu,Kanamori,2000),κ值随vS的变化而变化。根据式(1)至式(3)可以求解台站下方的地壳厚度和地壳平均波速比信息。
1.2 密度界面正演
密度界面的正反演主要用来研究地下的不连续界面,譬如盆地的沉积层基底、莫霍面的起伏等,主要有空间域和频率域两种方法。由于频率域方法计算快速精确,近年来得到了广泛的应用。二十世纪七十年代,Parker (1973,1974)首先提出了频率域重力位场的正演理论,而后Oldenburg (1974)给出了频率域重力密度界面的迭代反演理论。此后,基于Parker-Oldenburg方法,频率域密度界面正反演算法得到了快速的发展(冯锐,1986;Barbosa et al,1999;Silva et al,2006;Chakravarthi,Suncdararajan,2007;Feng et al,2014)。Feng等 (2014)基于前人的工作提出三维密度界面正演方程,其公式为
$$ \Delta g={{F}}^{-1}\left\{2\pi G{{\rm{e}}}^{-k{{\textit{z}}}_{0}}\sum\limits _{n=1}^{\infty }\frac{{ ( -k ) }^{n-1}}{n!}{F}\{\rho ( \xi , \eta ) \Delta {h}^{n}\}\right\}, $$ (4) 式中,$ \Delta g $为密度界面起伏引起的重力异常, ${F}\left\{\cdot\right\}$和$ {{F}}^{-1} \left\{\cdot \right\} $分别为傅里叶正变换和反变换,G为引力常数,k为波数, z0为参考界面的深度,$\; \rho ( \xi ,\eta ) $为界面上下的横向剩余密度差异,其中 $\xi \; 和 \; \eta$ 分别代表横向的正交方向,$ \Delta h $为界面深度相对于参考界面深度z0的差异。值得注意的是,在实际的密度界面正反演中,很难确定界面上下方剩余密度的横向差异,因此,如果把横向的剩余密度差异转换为常密度,式(4)与Parker (1973,1974)提出的常密度重力位场正演公式相同。
1.3 联合反演策略
接收函数和重力联合反演主要依赖于接收函数中的转换波(Ps)和莫霍面多次反射波(PpPs,PsPs+PpSs)相对于直达P波的到时信息和重力异常数据。联合反演的目标是找到一个最佳的莫霍面起伏和vP/vS模型来拟合接收函数不同震相的到时信息和重力异常数据。联合反演总的目标函数为
$$ \begin{split}&{M}_{{\rm{joint}}}=\frac{{\mu }_{1}}{2}{\Bigg(\frac{{T}_{\rm{{res}}}^{\rm{{Ps}}}-{T}_{\rm{{resMin}}}^{\rm{{Ps}}}}{{T}_{\rm{{resMax}}}^{\rm{{Ps}}}-{T}_{\rm{{resMin}}}^{\rm{{Ps}}}}\Bigg)}^{2}+\frac{{\mu }_{2}}{2}{\Bigg(\frac{{T}_{\rm{{res}}}^{{\rm{{PpPs}}}}-{T}_{\rm{{resMin}}}^{{\rm{{PpPs}}}}}{{T}_{\rm{{resMax}}}^{{\rm{{PpPs}}}}-{T}_{\rm{{resMin}}}^{{\rm{{PpPs}}}}}\Bigg)}^{2} +\\& \frac{{\mu }_{3}}{2}{\Bigg(\frac{{T}_{\rm{{res}}}^{{\rm{{PsPs}}}+{\rm{{PpSs}}}}-{T}_{\rm{{resMin}}}^{{\rm{{PsPs}}}+{\rm{{PpSs}}}}}{{T}_{\rm{{resMax}}}^{{\rm{{PsPs}}}+{\rm{{PpSs}}}}-{T}_{\rm{{resMin}}}^{{\rm{{PsPs}}}+{\rm{{PpSs}}}}}\Bigg)}^{2}+\frac{\gamma }{2}{\Bigg(\frac{{B}_{\rm{{res}}}-{B}_{\rm{{resMin}}}}{{B}_{\rm{{resMax}}}-{B}_{\rm{{resMin}}}}\Bigg)}^{2},\end{split} $$ (5) 式中:T和B代表接收函数和重力;T的上标表示转换波或多次波;T和B的下标中,resMax代表初始模型的最大剩余到时差或剩余重力异常,resMin代表当前模型下的最小剩余到时差或剩余重力异常,res为当前模型下的剩余到时或者剩余重力异常;$ \;{\mu }_{1} $,$ \;{\mu }_{2} $ 和$ \;{\mu }_{3} $分别为不同震相的权重系数;$ \gamma $为重力权重系数。我们把两种数据直接归并到一个反演系统中,将非线性反演简化为线性反演问题,反演策略与前人(Zhang et al,2014;Syracuse et al,2017)的联合反演研究类似。线性化的方程可表示为
$$ {{\boldsymbol{Gm}}}={{\boldsymbol{d}}},$$ (6) 式中,G为数据相对于模型的偏导数矩阵,m为当前模型矢量,d为数据的残差矢量。在实际的反演中加入正则化参数,联合反演的系统方程可以表示为
$$ \left[ {\begin{array}{*{20}{c}} {{\mu _1}G_{\rm{H}}^{{t_{{\rm{Ps}}}}}}&{{\mu _1}G_{\kappa}^{{t_{{\rm{Ps}}}}}}\\ {{\mu _1}G_{\rm{H}}^{{t_{{\rm{Ps}}}}}}&{{\mu _2}G_{\kappa}^{{t_{{{\rm{PpPs}}}}}}}\\ {{\mu _3}G_{\rm{H}}^{{t_{{{\rm{PsPs}}} + {{\rm{Pp}}}{{\rm{Ss}}}}}}}&{{\mu _3}G_{\kappa}^{{t_{{{\rm{PsPs}}} + {{\rm{Pp}}}{{\rm{Ss}}}}}}}\\ {\gamma G_{\rm{H}}^{\rm{B}}}&0\\ {{\varpi _{\rm{H}}}{{\boldsymbol{L}}_{\Delta H}}}&0\\ {{\lambda _{\rm{H}}}{\boldsymbol{I}}}&0\\ 0&{{\lambda _{{\rm{H}}}}{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta H}\\ {\Delta \kappa} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mu _1}{d^{{t_{{{\rm{Ps}}}}}}}}\\ {{\mu _2}{d^{{t_{{{\rm{PpPs}}}}}}}}\\ {{\mu _3}{d^{{t_{{{\rm{PsPs}}} + {{\rm{Pp}}}{{\rm{Ss}}}}}}}}\\ {\gamma {d^{\rm{B}}}}\\ 0\\ 0\\ 0 \end{array}} \right], $$ (7) 式中:联合反演系统的扰动模型m包含地壳(或莫霍面)的起伏扰动$ \Delta H $和波速比的扰动$ \Delta \kappa $;矩阵G的前三行代表了接收函数对于模型的扰动,上标${t}_{{{\rm{Ps}}}}$,${t}_{{{\rm{PpPs}}}}$和${t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}$分别代表转换波Ps和多次反射波PpPs,PsPs+PpSs,下标H为莫霍面模型,下标κ为波速比,其中,在实际的数据中,转换波Ps的波形质量一般高于多次反射波,因此反演方程中的权重为$\; {\mu }_{3}<{\mu }_{2} <{\mu }_{1} $;矩阵G的第四行包含了重力数据相对于莫霍面模型的偏导数,上标B代表布格重力数据,下标H代表莫霍面模型,γ为重力数据在联合反演中的权重,对于如何确定相关的权重系数,我们将在2.2节进行讨论;矩阵G的最后三行代表正则化参数,其中矩阵L表示一阶平滑约束,即在矩阵中的每一个点和不同方向的相邻点采用一阶差分平滑模型,$ {\varpi }_{H} $为求解莫霍面模型的平滑权重,通过对莫霍面平滑模型的约束可以间接地约束波速比κ,因此联合反演中没有对速度比κ进行平滑约束,I为单位矩阵,$ {\lambda }_{H} $和$ {\lambda }_{\kappa} $分别为莫霍面模型和波速比模型的阻尼权重参数。该联合反演系统可以通过阻尼最小二乘求解(Paige,Saunders,1982)。
在联合反演系统式(7)中,如何计算数据相对于模型的偏导数是解决问题的关键。对于接收函数转换波和多次反射波到时相对于模型的偏导数,依据式(1)至式(3)进行推导,可以得到:
$$ {G}_{{\rm{H}}}^{{t}_{{{\rm{Ps}}}}}=\frac{\partial {t}_{{{\rm{Ps}}}}}{\partial H}={M}_{1}-{M}_{2},$$ (8) $$ {G}_{\kappa}^{{t}_{{{\rm{Ps}}}}}=\frac{\partial {t}_{{{\rm{Ps}}}}}{\partial \kappa}=\frac{H\kappa}{{v}_{{\rm{P}}}^{2}{M}_{1}},$$ (9) $$ {G}_{{\rm{H}}}^{{t}_{{{\rm{PpPs}}}}}=\frac{\partial {t}_{{{\rm{PpPs}}}}}{\partial H}={M}_{1}+{M}_{2},$$ (10) $$ {G}_{\kappa}^{{t}_{{{\rm{PpPs}}}}}=\frac{\partial {t}_{{{\rm{PpPs}}}}}{\partial \kappa}=\frac{Hk}{{v}_{{\rm{P}}}^{2}{M}_{1}},$$ (11) $$ {G}_{{\rm{H}}}^{{t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}}=\frac{\partial {t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}}{\partial H}={2M}_{1},$$ (12) $$ {G}_{\kappa}^{{t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}}=\frac{\partial {t}_{{{\rm{PsPs}}}+{{\rm{PpSs}}}}}{\partial k}=\frac{2Hk}{{v}_{{\rm{P}}}^{2}{M}_{1}},$$ (13) $$ {M}_{1}=\sqrt{{\left(\frac{\kappa }{{\nu }_{{\rm{P}}}}\right)}^{2}-{p}^{2}},{M}_{2}=\sqrt{\frac{1}{{\nu }_{{\rm{P}}}^{2}}-{p}^{2}} {\text{.}} $$ (14) 对于重力数据而言,通过频率域的正演公式(4)无法直接求取重力数据相对于莫霍面模型的偏导数。为了简化问题,参考重力空间域迭代的算法(Cordell,Henderson,1968),假定重力异常的差异近似为地下无限平板状体引起。同时,重力异常随着深度急速衰减,为了平衡不同深度场源界面引起的重力异常,参考Li和Oldenburg (1998)重力三维反演中深度加权因子的概念和张盛和孟小红(2013)的界面起伏加权因子。重力数据相对于莫霍面的扰动可以近似表达为
$$ {G}_{{\rm{H}}}^{{\rm{B}}}=2\pi G\rho ( \xi ,\eta ) w ( {{\textit{z}}}_{0} ) ,$$ (15) 式中:G为万有引力常量;w (z0)= [ (z0+Δh)/z0 ] β为界面起伏加权项,z0为参考界面的深度,Δh为界面的起伏,β为界面起伏深度加权因子。当Δh为0时,w (z0)=1;当Δh大于0,位于参考界面上方时,w (z0)>1,压制浅部界面隆起;当Δh小于0,位于参考界面下方时,w (z0)<1,凸显深部界面。w (z0)作为界面起伏加权项,在反演过程中并无实际的物理意义,只是为了平衡参考界面上下方不同深度的界面权重。同时,在计算重力异常相对于莫霍面模型的偏导数矩阵时,也可以参考地球物理学联合反演成像领域的算法(Zhang et al,2014;Syracuse et al,2017;Han et al,2021),对待求解的模型进行扰动,通过差分方程获取近似解。
联合反演开始需要给定初始的莫霍面模型和速度比模型。初始模型可以给定一个大致的平均地壳参数模型,也可以利用传统的接收函数研究方法获得,如H-κ方法,H-β方法,H-κ-c方法。相对而言,给定的初始模型越靠近真实结果,迭代收敛越迅速(Zhang et al,2014;Syracuse et al,2017)。
2. 简单地壳模型测试
2.1 接收函数和重力正演
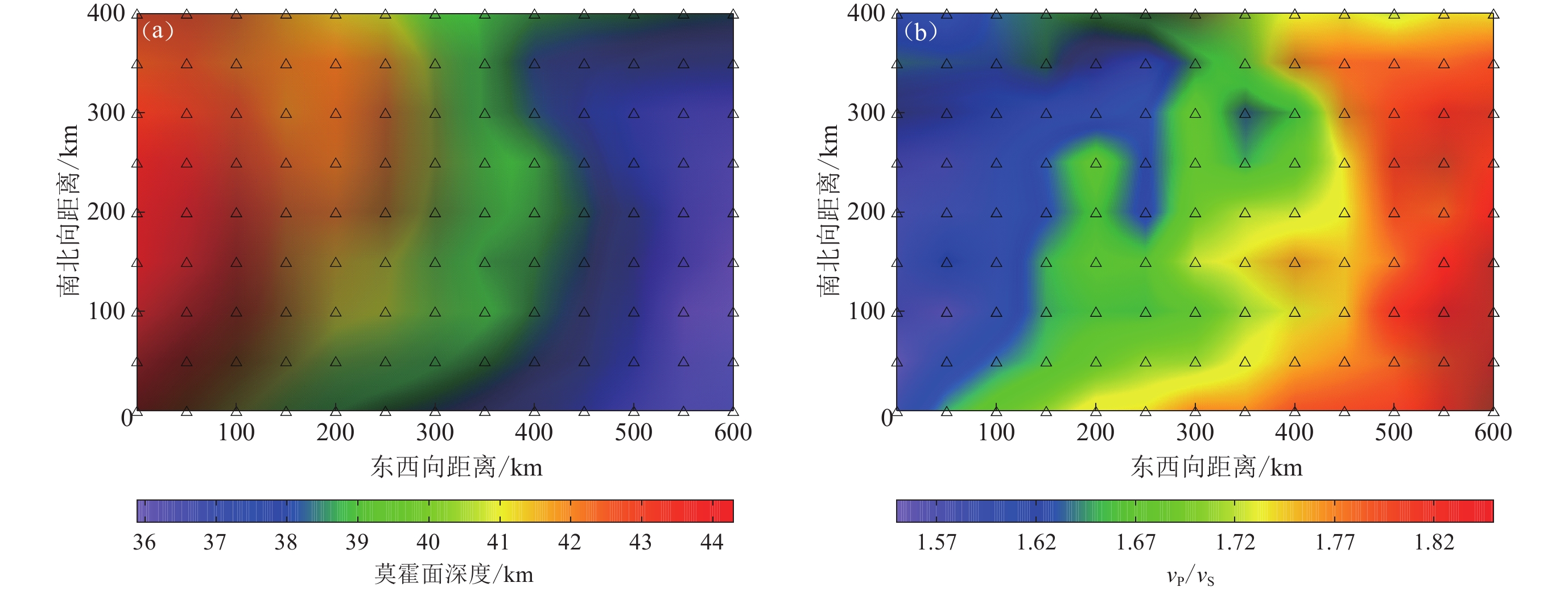
为了验证本文联合反演算法的有效性,首先建立简单的模型来进行测试。构建的莫霍面起伏模型和速度比模型分别见图1a和图1b,模型空间大小为600 km×400 km。虚拟台站在东西向和南北向的网格间距均为50 km。在实际的联合反演中,虚拟台站可以通过远震数据的波形重建来完成(Pavlis,2011;Zhang,Zheng,2015;Chai et al,2015;Song et al,2017;张雪敏等,2019;Hu et al,2019)。此外,在合成数据测试中,假定观测面为海平面,忽略地形的起伏。图1a中莫霍面变化的范围为45—35 km,平均值为40 km,其整体趋势为自西向东逐渐依次递减;图1b所示的地壳平均速度比自西向东依次递增,其变化范围为1.55—1.83,平均值为1.68。
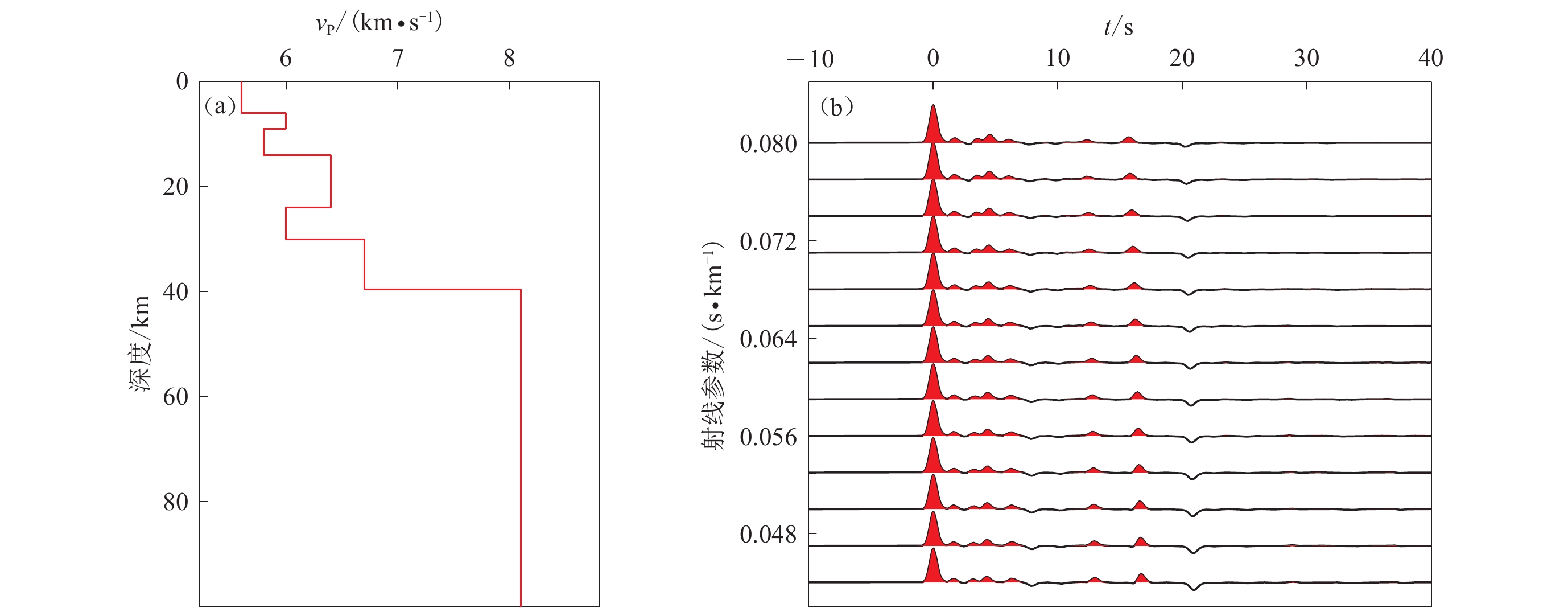
为了说明如何构建联合反演系统以及如何确定相关反演参数,我们通过建立的壳幔模型来演示整个反演流程。假定莫霍面上方的vP=6.3 km/s,莫霍面下方的vP=8.0 km/s。以图1中的一个台站(HMoho=39.6 km,κ=1.65)为例,其速度分布和合成的接收函数分别见图2,在纵向的时间轴上可以清晰地看到转换波Ps及其后续的多次波。每一个台站的转换波和多次波相对于直达P波的相对到时可以通过波形的叠加获取。对于莫霍面起伏引起的重力异常,可以通过正演公式(4)来计算。模型测试中假定参考界面的深度为40 km,上下界面的剩余密度为500 g/cm3。图1a中莫霍面起伏所引起的重力异常如图2c所示,可见重力异常的范围为−89.89×10−5 m/s2至86.12×10−5 m/s2,整体的变化趋势为自西向东递增。
![]() 图 2 虚拟台站(东向坐标x=350 km,北向坐标y=250 km)下方的简单P波速度结构(a)和根据该模型正演出的对应不同射线参数的理论接收函数(b),以及图1a中莫霍面起伏所引起的重力异常(c)Figure 2. The simple crustal P-wave velocity structure beneath one virtual seismic station at x=350 km in the east direction and y=250 km in the north direction (a),and the theoretical receiver functions for different ray parameters (b),and gravity anomalies caused by Moho variations in Fig.1a (c)
图 2 虚拟台站(东向坐标x=350 km,北向坐标y=250 km)下方的简单P波速度结构(a)和根据该模型正演出的对应不同射线参数的理论接收函数(b),以及图1a中莫霍面起伏所引起的重力异常(c)Figure 2. The simple crustal P-wave velocity structure beneath one virtual seismic station at x=350 km in the east direction and y=250 km in the north direction (a),and the theoretical receiver functions for different ray parameters (b),and gravity anomalies caused by Moho variations in Fig.1a (c)2.2 反演过程
在实际的台站获取的数据中,由于地壳内部介质不均一或浅部沉积层的存在,很难得到图2中的高质量接收函数数据和重力异常数据,为此我们分别为提取到的理论转换波、多次波的到时信息和重力异常加入一定幅度的随机噪声干扰。对于转换波Ps和多次反射波PpPs,PsPs+PpSs分别加入5%,7%和10%幅值的高斯噪声,为重力数据加入了10%的高斯噪声。此外,在反演过程中,选取vP为6.3 km/s,剩余密度为500 g/cm3,重力的界面参考深度为平均深度40 km。
2.2.1 参数确定
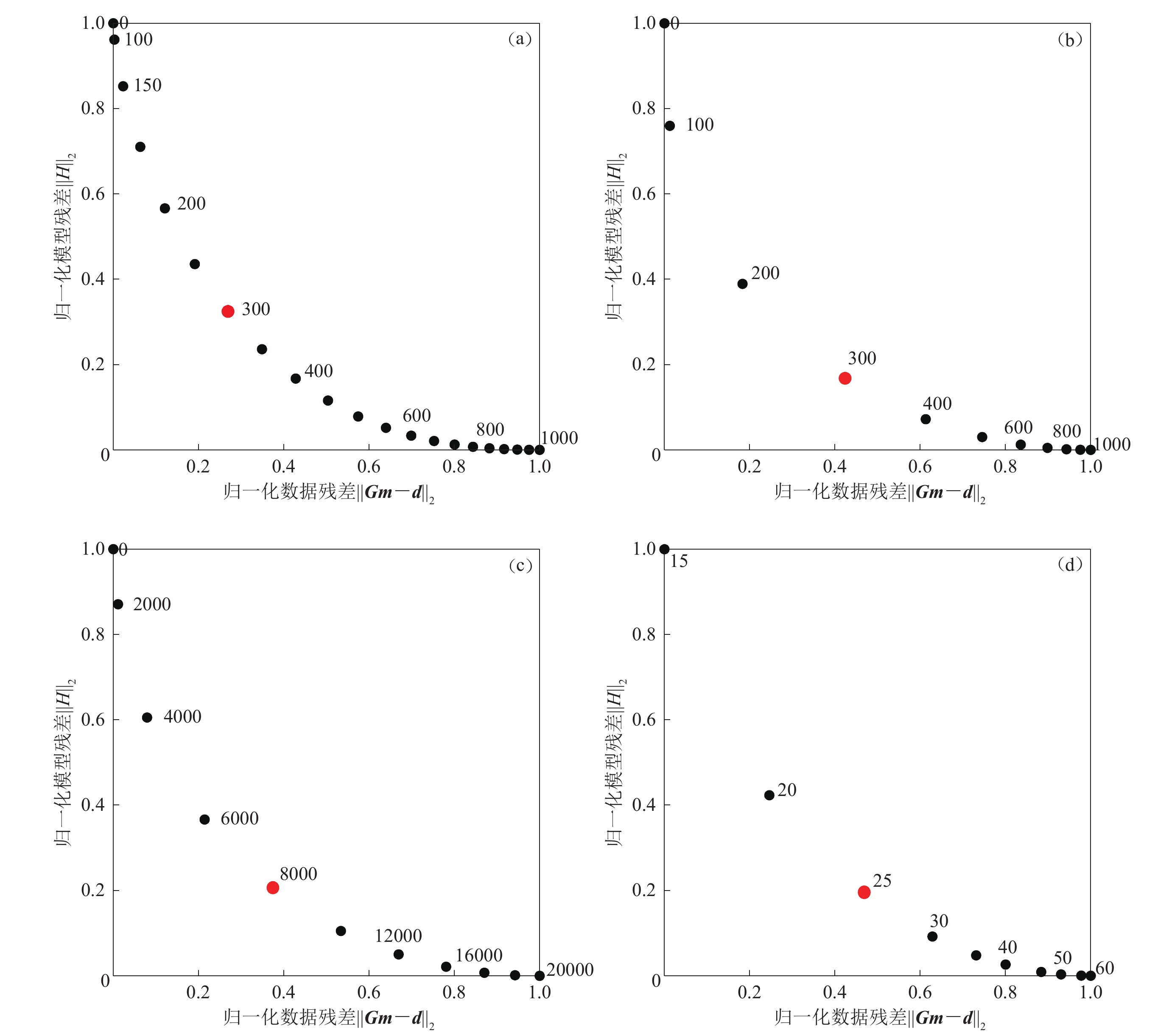
在进行联合反演之前,需要确定相关的正则化参数和不同数据的权重,通常选用L-曲线分析方法来选择参数的最优值(Aster et al,2013)。为了能够更加高效地确定平滑参数$ {\varpi }_{{\rm{M}}} $和阻尼参数(${\lambda }_{{\rm{M}}},{\lambda }_{\kappa}$),首先只利用接收函数的到时数据来反演(此时$ \;{\mu }_{1}=1 $,$ \;{\mu }_{2}=0.5 $,$ {\mu }_{3}=0.2 $,$ \gamma =0 $),接收函数权重系数的选取参考H-κ方法中不同震相的权重(Zhu,Kanamori,2000),以确保前面相对清晰的震相权重约为后续震相的两倍左右,其结果见图3。图3a,b,c中仅通过接收函数方法确定L-曲线的最佳选择点,其中平滑参数和阻尼参数的最佳点分别为${\varpi }_{{\rm{M}}}=300$,${\lambda }_{{\rm{M}}}=300$,$ {\lambda }_{\kappa}=8\;000 $ ;而后,我们利用接收函数和重力两种不同数据的L-曲线确定重力的最优权重$ \gamma =25 $。
![]() 图 3 联合反演L-曲线分析(a,b,c)通过接收函数确定的不同平滑参数和阻尼参数下的归一化模型与数据残差的关系,最优参数$ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,$ {\lambda }_{k}=8\;000 $;(d) 接收函数与重力之间权重关系曲线,重力的最优参数$ \gamma =25 $Figure 3. L-curve analysis for the joint inversion(a,b,c) Trade-off between the normalized model residuals and data residuals for different smoothing or damping parameters used in receiver function inversion ($ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,${\lambda }_{\kappa}=8\;000$); (d) Tradeoff analysis between the normalized model residuals and data residuals for different weights between receiver function and gravity data,and the optimal weight $ \gamma =25 $
图 3 联合反演L-曲线分析(a,b,c)通过接收函数确定的不同平滑参数和阻尼参数下的归一化模型与数据残差的关系,最优参数$ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,$ {\lambda }_{k}=8\;000 $;(d) 接收函数与重力之间权重关系曲线,重力的最优参数$ \gamma =25 $Figure 3. L-curve analysis for the joint inversion(a,b,c) Trade-off between the normalized model residuals and data residuals for different smoothing or damping parameters used in receiver function inversion ($ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,${\lambda }_{\kappa}=8\;000$); (d) Tradeoff analysis between the normalized model residuals and data residuals for different weights between receiver function and gravity data,and the optimal weight $ \gamma =25 $2.2.2 联合反演结果
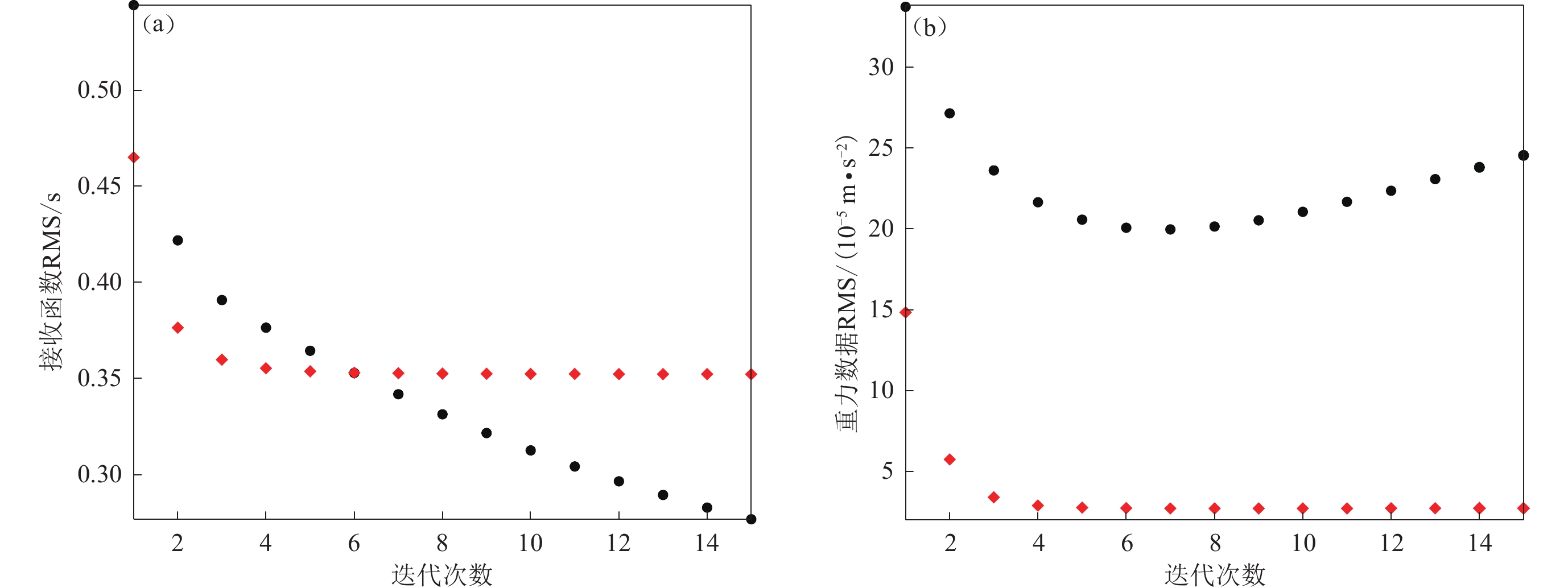
根据上节确定的反演参数进行阻尼最小二乘法的迭代反演,其反演过程需给出初始模型。选择所有台站的平均值作为初始模型,即假定所有台站下的莫霍面深度均为40 km,vP/vS=1.68。反演的目标是拟合接收函数到时信息和重力异常数据。图4中分别给出了只采用接收函数反演和采用联合反演对接收函数到时和重力异常数据的拟合情况。如果我们只进行接收函数反演,对于接收函数不同震相到时可以拟合得很好(图4a中的黑色圆点),但不能有效地拟合重力数据(图4b中的黑色圆点)。如果采用联合反演,可以同时拟合接收函数和重力异常两种数据(图4中的红色方块),同时提高反演的迭代效率,本次测试在迭代四次之后基本稳定。
![]() 图 4 (a) 接收函数的RMS迭代收敛曲线;(b) 重力异常的RMS迭代收敛曲线图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果Figure 4. (a) The RMS residuals of receiver function;(b) The RMS residuals of gravity dataThe black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion
图 4 (a) 接收函数的RMS迭代收敛曲线;(b) 重力异常的RMS迭代收敛曲线图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果Figure 4. (a) The RMS residuals of receiver function;(b) The RMS residuals of gravity dataThe black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion以图4中迭代15次之后的结果为例来分析相关结果的差异。莫霍面的结果见图5a-5d,其中图5a和图5b分别为接收函数反演和联合反演得到的莫霍面起伏结果,其界面的起伏形态基本一致。但与理论模型相比,接收函数反演结果与理论模型的误差最大可达2.7 km (所有台站的标准差为1.15 km),而联合反演模型的误差最大只有0.52 km (所有台站的标准差为0.22 km)。因此联合反演结果明显优于只采用单一接收函数反演结果,可以更好地恢复莫霍面的模型。
![]() 图 5 (a,b) 仅采用接收函数数据反演和联合反演获取的莫霍面;(c,d) 采用接收函数反演和联合反演所获取的莫霍面结果与理论模型的残差分布;(e,f) 采用接收函数和联合反演得到的地壳平均波速比;(g,h) 反演的平均地壳波速比结果与理论模型之间的残差Figure 5. (a,b) The Moho results determined by receiver function analysis and joint inversion,respectively; (c,d) The deviations of inverted Moho models in Figs.(a) and (b) from theoretical Moho model in Fig. 1a,respectively;(e,f) The average crustal vP/vS ratios by receiver function analysis and joint inversion,respectively; (g,h) The deviations of inverted vP/vS models in Figs. (e) and (f) from the theoretical vP/vS model in Fig. 1b,respectively
图 5 (a,b) 仅采用接收函数数据反演和联合反演获取的莫霍面;(c,d) 采用接收函数反演和联合反演所获取的莫霍面结果与理论模型的残差分布;(e,f) 采用接收函数和联合反演得到的地壳平均波速比;(g,h) 反演的平均地壳波速比结果与理论模型之间的残差Figure 5. (a,b) The Moho results determined by receiver function analysis and joint inversion,respectively; (c,d) The deviations of inverted Moho models in Figs.(a) and (b) from theoretical Moho model in Fig. 1a,respectively;(e,f) The average crustal vP/vS ratios by receiver function analysis and joint inversion,respectively; (g,h) The deviations of inverted vP/vS models in Figs. (e) and (f) from the theoretical vP/vS model in Fig. 1b,respectively图5e-5h为速度比vP/vS的反演结果,接收函数反演(图5e)和联合反演(图5f)都较好地恢复了理论模型,整体的形态差异不大。接收函数单一反演和联合反演所获取的速度比模型与理论模型(图1b)之间的残差分布分别见图5g (最大差异为0.06,平均标准差为0.026)和图5h (最大差异为0.04,标准差为0.023),可见联合反演较好地恢复了vP/vS模型。
3. 复杂地壳模型测试
这一节进一步测试复杂地壳结构情况下的重力和接收函数联合反演算法。在新的模型中,莫霍面的起伏变化与图1a中所显示的一致,但是地壳P波速度不是均匀的,而是分为六层,速度在5.6 km/s至6.8 km/s之间变化,其中包含两个低速层。当地壳中包含低速层时,远震P波在莫霍面的转换波和莫霍面引起的多次波会受到较大干扰,特别是对于转换波Ps (图6b)。此时采用传统方法,譬如H-κ方法,很难有效地获取地壳厚度和速度比参数(Tao et al,2014;Shi et al,2018;Guo et al,2019)。
我们同样对上述接收函数的转换波到时数据Ps和多次波PpPs,PSPs+PpSs分别加入5%,7%和10%的随机噪声,对于重力数据同样加入10%幅值的高斯随机噪声,反演的参数与简单地壳参数相同。在接收函数和重力数据的双重约束下,联合反演可以快速达到收敛,同时尽可能避免拟合更多的噪声(图7)。反演后迭代稳定的结果与原始的莫霍面和速度比的残差见图8,可见:只采用接收函数到时信息反演得到的莫霍面模型与原始模型差异的最大值为3.9 km,所有台站的平均均方差为1.51 km (图8a),而采用联合反演获取的莫霍面模型与原始模型残差的最大值为0.53 km,所有台站的平均标准差为0.25 km (图8b)。对比图8a与图8b可知,在复杂地壳结构模型下,联合反演可以有效地提高莫霍面深度的计算精度。对于只采用接收函数反演的速度比模型结果见图8c,其残差的最大值为0.16,所有台站的平均标准差为0.041。比较而言,联合反演的残差最大值为0.14,所有台站的平均标准差为0.035 8,这说明采用联合反演方案对于速度比模型有一定的提升。
![]() 图 7 复杂速度模型情况下接收函数(a)和重力异常(b)的RMS迭代收敛曲线图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果Figure 7. The RMS residuals of receiver function data (a) and gravity data (b) with iterations for the complex velocity modelThe black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion
图 7 复杂速度模型情况下接收函数(a)和重力异常(b)的RMS迭代收敛曲线图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果Figure 7. The RMS residuals of receiver function data (a) and gravity data (b) with iterations for the complex velocity modelThe black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion![]() 图 8 只采用接收函数反演(a)和联合反演(b)得到的莫霍面结果与原始模型的残差以及只采用接收函数反演(c)和联合反演(d)获取的速度比结果与原始模型的残差Figure 8. Deviations between theoretical Moho model in Fig. 1a and the inverted Moho models from only receiver functions (a) and joint inversion (b),and deviations between theoretical vP/vS model in Fig. 1b and the inverted vP/vS models from only receiver functions (c) and joint inversion (d),respectively
图 8 只采用接收函数反演(a)和联合反演(b)得到的莫霍面结果与原始模型的残差以及只采用接收函数反演(c)和联合反演(d)获取的速度比结果与原始模型的残差Figure 8. Deviations between theoretical Moho model in Fig. 1a and the inverted Moho models from only receiver functions (a) and joint inversion (b),and deviations between theoretical vP/vS model in Fig. 1b and the inverted vP/vS models from only receiver functions (c) and joint inversion (d),respectively综上,采用联合反演方法可以很好地拟合接收函数到时数据和重力异常数据,测试中引起的误差主要是我们对接收函数到时和重力数据加入的高斯随机误差。本文提出的联合反演算法相对于单独接收函数到时反演而言,莫霍面的计算精度有较大的提升,同时引入重力数据的约束也可以间接地约束波速比,使反演结果更加准确。
4. 联合反演相关参数敏感度测试
在均匀地壳模型和复杂地壳模型测试中,验证了本文提出的联合反演方法的有效性。在上述的联合反演中,我们选取的反演参数vP为6.3 km/s,壳幔的密度差为500 kg/m3,重力数据正演的参考界面深度为40 km。以复杂地壳模型为例(图6a),分别采用控制单一变量的方法来测试不同反演参数对反演结果的影响。
4.1 地壳平均vP
在复杂地壳结构模型中,vP的变化范围为5.6—6.8 km/s。在联合反演中,我们将vP从6.0 km/s变化至6.6 km/s,得到的结果详见表1。由于重力数据的横向约束,不同的vP对莫霍面的反演精度影响较小,引起的莫霍面最大误差在0.526—0.664 km之间,所有台站的标准差在0.249—0.286 km之间。对于波速比而言,采用不同的vP对反演结果的影响较大,不同vP参数下误差范围处于0.123—0.177之间。但是,由于重力数据的引入,联合反演所得波速比整体误差较小。
表 1 不同P波速度对联合反演的影响Table 1. The effect of different P-wave velocities on joint inversionvP
/(km·s−1)联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 6.0 0.362 2.905 0.664 0.285 0.177 0.041 6.1 0.361 2.842 0.607 0.263 0.164 0.033 6.2 0.363 2.794 0.554 0.251 0.152 0.033 6.3 0.363 2.743 0.526 0.249 0.139 0.041 6.4 0.363 2.695 0.569 0.256 0.126 0.054 6.5 0.362 2.649 0.612 0.268 0.123 0.062 6.6 0.364 2.602 0.653 0.286 0.142 0.068 4.2 壳幔剩余密度
壳幔剩余密度的选择对联合反演系统也会产生影响,此处选择350—650 kg/m3范围内的剩余密度参数进行测试。对于重力界面反演而言,剩余密度相对于真实密度差过小会加大界面的起伏,过大则会使结果过于平滑。相对于传统的密度界面重力反演,引入接收函数可以减少莫霍面反演的不确定性。由表2可见:不同剩余密度下的台站下方莫霍面反演的误差最大值处于0.529—1.41 km之间,标准差处于0.249—0.794 km之间;台站下方波速比最大误差处于0.121—0.168之间,但波速比的整体误差比较稳定,其标准差在0.040—0.055之间。
表 2 不同剩余密度参数对联合反演结果的影响Table 2. Effect of different contrast densities on joint inversion剩余密度
/(kg·m−3)联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 350 0.375 6.550 1.410 0.794 0.168 0.055 400 0.371 3.560 1.150 0.638 0.156 0.048 450 0.364 3.070 0.940 0.372 0.147 0.044 500 0.363 2.740 0.529 0.249 0.139 0.041 550 0.365 2.510 0.710 0.318 0.132 0.040 600 0.368 2.330 0.990 0.456 0.126 0.040 650 0.372 2.190 1.250 0.595 0.121 0.041 4.3 重力界面参考深度
在联合反演中,需要给定参考界面的深度作为已知信息。在前期的测试中我们选用地壳平均深度为40 km,这里我们改变参考界面深度来测试其对反演结果的影响。深度变化范围设置为38.5—41.5 km,结果详见表3。因为实际的地壳深度参数接近平均深度40 km,因此设定参考界面的深度为40 km时,得到的莫霍面误差相对越小。参考界面的选择对莫霍面的影响相对较大,而对速度比的影响相对较小。
表 3 不同参考界面深度对联合反演影响Table 3. Effect of different reference interfaces on joint inversion参考深度/km 联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 38.5 0.363 2.745 1.908 1.410 0.136 0.076 39.0 0.363 2.745 1.439 0.953 0.121 0.063 39.5 0.363 2.745 0.971 0.515 0.130 0.051 40.0 0.363 2.743 0.529 0.249 0.139 0.041 40.5 0.363 2.742 0.994 0.545 0.148 0.034 41.0 0.363 2.742 1.463 0.986 0.156 0.032 41.5 0.363 2.743 1.931 1.444 0.165 0.034 5. 讨论与结论
本文提出了一种接收函数和重力联合反演算法,通过同时拟合多个台站的接收函数和重力数据来获取区域的莫霍面起伏和地壳平均波速比变化,简单地壳模型和复杂地壳模型的测试均表明了联合反演算法的有效性,主要结论如下:
1) 重力数据的约束可以提高单一接收函数反演的不确定性,有效地提高莫霍面反演的可靠性和反演系统的稳定性。
2) 联合反演系统相关参数敏感度测试显示,当这些参数选择在合理值区间时,联合反演的结果对这些参数的依赖性较低。整体而言,在联合反演系统中,地壳平均vP的选择对波速比反演结果更敏感,而壳幔剩余密度和重力参考界面参数的选择对莫霍面反演结果更敏感。
3) 本文提出的接收函数和重力联合反演算法,依赖于规则的虚拟地震台阵,在实际应用中,需要考虑地震台站的空间位置、台站间距和波形质量等信息重建规则的虚拟台站。
4) 对于波形重建后的接收函数不同震相到时的拾取,可以通过参考模型先计算出理论到时,然后在附近搜索最大幅值对应的到时即可自动实现。
本文更多关注的是联合反演算法的理论测试,在后续的研究中,我们将对实际数据进行处理和讨论,进一步发展本文提出的联合反演算法。
-
图 5 (a,b) 仅采用接收函数数据反演和联合反演获取的莫霍面;(c,d) 采用接收函数反演和联合反演所获取的莫霍面结果与理论模型的残差分布;(e,f) 采用接收函数和联合反演得到的地壳平均波速比;(g,h) 反演的平均地壳波速比结果与理论模型之间的残差
Figure 5. (a,b) The Moho results determined by receiver function analysis and joint inversion,respectively; (c,d) The deviations of inverted Moho models in Figs.(a) and (b) from theoretical Moho model in Fig. 1a,respectively;(e,f) The average crustal vP/vS ratios by receiver function analysis and joint inversion,respectively; (g,h) The deviations of inverted vP/vS models in Figs. (e) and (f) from the theoretical vP/vS model in Fig. 1b,respectively
图 2 虚拟台站(东向坐标x=350 km,北向坐标y=250 km)下方的简单P波速度结构(a)和根据该模型正演出的对应不同射线参数的理论接收函数(b),以及图1a中莫霍面起伏所引起的重力异常(c)
Figure 2. The simple crustal P-wave velocity structure beneath one virtual seismic station at x=350 km in the east direction and y=250 km in the north direction (a),and the theoretical receiver functions for different ray parameters (b),and gravity anomalies caused by Moho variations in Fig.1a (c)
图 3 联合反演L-曲线分析
(a,b,c)通过接收函数确定的不同平滑参数和阻尼参数下的归一化模型与数据残差的关系,最优参数$ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,$ {\lambda }_{k}=8\;000 $;(d) 接收函数与重力之间权重关系曲线,重力的最优参数$ \gamma =25 $
Figure 3. L-curve analysis for the joint inversion
(a,b,c) Trade-off between the normalized model residuals and data residuals for different smoothing or damping parameters used in receiver function inversion ($ {\varpi }_{H}=300 $,$ {\lambda }_{H}=300 $,${\lambda }_{\kappa}=8\;000$); (d) Tradeoff analysis between the normalized model residuals and data residuals for different weights between receiver function and gravity data,and the optimal weight $ \gamma =25 $
图 4 (a) 接收函数的RMS迭代收敛曲线;(b) 重力异常的RMS迭代收敛曲线
图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果
Figure 4. (a) The RMS residuals of receiver function;(b) The RMS residuals of gravity data
The black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion
图 7 复杂速度模型情况下接收函数(a)和重力异常(b)的RMS迭代收敛曲线
图中黑色圆点为只采用接收函数到时数据,红色方块为采用接收函数和重力异常两种数据联合反演的结果
Figure 7. The RMS residuals of receiver function data (a) and gravity data (b) with iterations for the complex velocity model
The black dots denote the results only by receiver function data,and the red diamonds denote the results by joint inversion
图 8 只采用接收函数反演(a)和联合反演(b)得到的莫霍面结果与原始模型的残差以及只采用接收函数反演(c)和联合反演(d)获取的速度比结果与原始模型的残差
Figure 8. Deviations between theoretical Moho model in Fig. 1a and the inverted Moho models from only receiver functions (a) and joint inversion (b),and deviations between theoretical vP/vS model in Fig. 1b and the inverted vP/vS models from only receiver functions (c) and joint inversion (d),respectively
表 1 不同P波速度对联合反演的影响
Table 1 The effect of different P-wave velocities on joint inversion
vP
/(km·s−1)联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 6.0 0.362 2.905 0.664 0.285 0.177 0.041 6.1 0.361 2.842 0.607 0.263 0.164 0.033 6.2 0.363 2.794 0.554 0.251 0.152 0.033 6.3 0.363 2.743 0.526 0.249 0.139 0.041 6.4 0.363 2.695 0.569 0.256 0.126 0.054 6.5 0.362 2.649 0.612 0.268 0.123 0.062 6.6 0.364 2.602 0.653 0.286 0.142 0.068 表 2 不同剩余密度参数对联合反演结果的影响
Table 2 Effect of different contrast densities on joint inversion
剩余密度
/(kg·m−3)联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 350 0.375 6.550 1.410 0.794 0.168 0.055 400 0.371 3.560 1.150 0.638 0.156 0.048 450 0.364 3.070 0.940 0.372 0.147 0.044 500 0.363 2.740 0.529 0.249 0.139 0.041 550 0.365 2.510 0.710 0.318 0.132 0.040 600 0.368 2.330 0.990 0.456 0.126 0.040 650 0.372 2.190 1.250 0.595 0.121 0.041 表 3 不同参考界面深度对联合反演影响
Table 3 Effect of different reference interfaces on joint inversion
参考深度/km 联合反演RMS拟合 联合反演残差 莫霍面深度/km vP/vS 接收函数/s 重力异常/(10−5 m·s−2) 最大残差 标准差 最大残差 标准差 38.5 0.363 2.745 1.908 1.410 0.136 0.076 39.0 0.363 2.745 1.439 0.953 0.121 0.063 39.5 0.363 2.745 0.971 0.515 0.130 0.051 40.0 0.363 2.743 0.529 0.249 0.139 0.041 40.5 0.363 2.742 0.994 0.545 0.148 0.034 41.0 0.363 2.742 1.463 0.986 0.156 0.032 41.5 0.363 2.743 1.931 1.444 0.165 0.034 -
冯锐. 1986. 三维物性分布的位场计算[J]. 地球物理学报,29(4):399–406. doi: 10.3321/j.issn:0001-5733.1986.04.010 Feng R. 1986. A computation method of potential field with three-dimensional density and magnetization distributions[J]. Acta Geophysica Sinica,29(4):399–406 (in Chinese).
郭良辉,孟小红,石磊,陈召曦. 2012. 优化滤波方法及其在中国大陆布格重力异常数据处理中的应用[J]. 地球物理学报,55(12):4078–4088. doi: 10.6038/j.issn.0001-5733.2012.12.020 Guo L H,Meng X H,Shi L,Chen Z X. 2012. Preferential filtering method and its application to Bouguer gravity anomaly of Chinese continent[J]. Chinese Journal of Geophysics,55(12):4078–4088 (in Chinese).
宋婷,沈旭章,梅秀苹. 2020. 利用接收函数频率特征研究莫霍面形态及应用[J]. 地震学报,42(2):135–150. doi: 10.11939/jass.20190149 Song T,Shen X Z,Mei X P. 2020. Constraining Moho characteristics with frequency-dependence of receiver function and its application[J]. Acta Seismologica Sinica,42(2):135–150 (in Chinese).
张洪双,田小波,滕吉文. 2009. 接收函数方法估计Moho倾斜地区的地壳速度比[J]. 地球物理学报,52(5):1243–1252. doi: 10.3969/j.issn.0001-5733.2009.05.013 Zhang H S,Tian X B,Teng J W. 2009. Estimation of crustal vP/vS with dipping Moho from receiver functions[J]. Chinese Journal of Geophysics,52(5):1243–1252 (in Chinese).
张盛,孟小红. 2013. 约束变密度界面反演方法[J]. 地球物理学进展,28(4):1714–1720. doi: 10.6038/pg20130411 Zhang S,Meng X H. 2013. Constraint interface inversion with variable density model[J]. Progress in Geophysics,28(4):1714–1720 (in Chinese).
张雪敏,付丽华,张海江,彭佳明. 2019. 基于正交秩-1矩阵追踪的天然地震数据重建研究:以加州San Jacinto断层密集地震台阵为例[J]. 地球物理学报,62(4):1427–1439. doi: 10.6038/cjg2019M0352 Zhang X M,Fu L H,Zhang H J,Peng J M. 2019. Reconstruction of natural earthquake data based on Orthogonal Rank-one Matrix Pursuit and its application to dense seismic array around the San Jacinto fault zone in California[J]. Chinese Journal of Geophysics,62(4):1427–1439 (in Chinese).
Aitken A R A. 2010. Moho geometry gravity inversion experiment (MoGGIE):A refined model of the Australian Moho,and its tectonic and isostatic implications[J]. Earth Planet Sci Lett,297(1/2):71–83.
Aitken A R A,Salmon M L,Kennett B L N. 2013. Australia’s Moho:A test of the usefulness of gravity modelling for the determination of Moho depth[J]. Tectonophysics,609:468–479. doi: 10.1016/j.tecto.2012.06.049
Aster R C, Borchers B, Thurber C H. 2013. Parameter Estimation and Inverse Problems[M]. 2nd ed. Burlington, MA, USA: Academic Press: 93–95.
Barbosa V C F,Silva J B C,Medeiros W E. 1999. Stable inversion of gravity anomalies of sedimentary basins with nonsmooth basement reliefs and arbitrary density contrast variations[J]. Geophysics,64(3):754–764. doi: 10.1190/1.1444585
Chai C P,Ammon C J,Maceira M,Herrmann R B. 2015. Inverting interpolated receiver functions with surface wave dispersion and gravity:Application to the western U.S. and adjacent Canada and Mexico[J]. Geophys Res Lett,42(11):4359–4366. doi: 10.1002/2015GL063733
Chakravarthi V,Sundararajan N. 2007. 3D gravity inversion of basement relief:A depth-dependent density approach[J]. Geophysics,72(2):I23–I32. doi: 10.1190/1.2431634
Cordell L,Henderson R G. 1968. Iterative three-dimensional solution of gravity anomaly data using a digital computer[J]. Geophysics,33(4):596–601. doi: 10.1190/1.1439955
Feng J,Meng X H,Chen Z X,Zhang S. 2014. Three-dimensional density interface inversion of gravity anomalies in the spectral domain[J]. J Geophys Eng,11(3):035001. doi: 10.1088/1742-2132/11/3/035001
Guo L H,Gao R,Shi L,Huang Z R,Ma Y W. 2019. Crustal thickness and Poisson’s ratios of South China revealed from joint inversion of receiver function and gravity data[J]. Earth Planet Sci Lett,510:142–152. doi: 10.1016/j.jpgl.2018.12.039
Han S C,Zhang H J,Xin H L,Shen W S,Yao H J. 2021. USTClitho2.0:Updated unified seismic tomography models for continental China lithosphere from joint inversion of body-wave arrival times and surface-wave dispersion data[J]. Seismol Res Lett,93(1):201–215.
He R Z,Shang X F,Yu C Q,Zhang H J,van der Hilst R D. 2014. Detailed Moho depth mapping of continental China by receiver function analysis[J]. Geophys J Int,199:1910–1918. doi: 10.1093/gji/ggu365
Hu S Q,Jiang X H,Zhu L P,Yao H J. 2019. Wavefield reconstruction of teleseismic receiver function with the stretching-and-squeezing interpolation method[J]. Seismol Res Lett,90(2A):716–726. doi: 10.1785/0220180197
Julià J,Mejía J. 2004. Thickness and vP/vS ratio variation in the Iberian crust[J]. Geophys J Int,156(1):59–72. doi: 10.1111/j.1365-246X.2004.02127.x
Li J T,Song X D,Wang P,Zhu L P. 2019. A generalized H-κ method with harmonic corrections on Ps and its crustal multiples in receiver functions[J]. J Geophys Res:Solid Earth,124(4):3782–3801. doi: 10.1029/2018JB016356
Li Y G,Oldenburg D W. 1998. 3-D inversion of gravity data[J]. Geophysics,63(1):109–119. doi: 10.1190/1.1444302
Li Y H,Gao M T,Wu Q J. 2014. Crustal thickness map of the Chinese mainland from teleseismic receiver functions[J]. Tectonophysics,611:51–60. doi: 10.1016/j.tecto.2013.11.019
Lowry A R,Pérez-Gussinyé M. 2011. The role of crustal quartz in controlling Cordilleran deformation[J]. Nature,471(7338):353–357. doi: 10.1038/nature09912
Maceira M,Ammon C J. 2009. Joint inversion of surface wave velocity and gravity observations and its application to central Asian basins shear velocity structure[J]. J Geophys Res:Solid Earth,114(B2):B02314.
Niu F L,Bravo T,Pavlis G,Vernon F,Rendon H,Bezada M,Levander A. 2007. Receiver function study of the crustal structure of the southeastern Caribbean plate boundary and Venezuela[J]. J Geophys Res:Solid Earth,112(B11):B11308. doi: 10.1029/2006JB004802
Oldenburg D W. 1974. The inversion and interpretation of gravity anomalies[J]. Geophysics,39(4):526–536. doi: 10.1190/1.1440444
Owens T J,Zandt G. 1997. Implications of crustal property variations for models of Tibetan Plateau evolution[J]. Nature,387(6628):37–43. doi: 10.1038/387037a0
Paige C C,Saunders M A. 1982. LSQR:An algorithm for sparse linear equations and sparse least squares[J]. CAM Trans Math Softw,8(1):43–71. doi: 10.1145/355984.355989
Parker R L. 1973. The rapid calculation of potential anomalies[J]. Geophys J R astr Soc,31(4):447–455. doi: 10.1111/j.1365-246X.1973.tb06513.x
Parker R L. 1974. Best bounds on density and depth from gravity data[J]. Geophysics,39(5):644–649. doi: 10.1190/1.1440454
Pavlis G L. 2011. Three-dimensional,wavefield imaging of broadband seismic array data[J]. Comput Geosci,37(8):1054–1066. doi: 10.1016/j.cageo.2010.11.015
Shi L,Guo L H,Ma Y W,Li Y H,Wang W L. 2018. Estimating crustal thickness and vP/vS ratio with joint constraints of receiver function and gravity data[J]. Geophys J Int,213(2):1334–1344. doi: 10.1093/gji/ggy062
Silva J B,Costa D C,Barbosa V C. 2006. Gravity inversion of basement relief and estimation of density contrast variation with depth[J]. Geophysics,71(5):J51–J58. doi: 10.1190/1.2236383
Song P H,Zhang X M,Liu Y S,Teng J W. 2017. Moho imaging based on receiver function analysis with teleseismic wavefield reconstruction:Application to South China[J]. Tectonophysics,718:118–131. doi: 10.1016/j.tecto.2017.05.031
Syracuse E M,Maceira M,Prieto G A,Zhang H J,Ammon C J. 2016. Multiple plates subducting beneath Colombia,as illuminated by seismicity and velocity from the joint inversion of seismic and gravity data[J]. Earth Planet Sci Lett,444:139–149. doi: 10.1016/j.jpgl.2016.03.050
Syracuse E M,Zhang H J,Maceira M. 2017. Joint inversion of seismic and gravity data for imaging seismic velocity structure of the crust and upper mantle beneath Utah,United States[J]. Tectonophysics,718:105–117. doi: 10.1016/j.tecto.2017.07.005
Tao K,Liu T Z,Ning J Y,Niu F L. 2014. Estimating sedimentary and crustal structure using wavefield continuation:Theory,techniques and applications[J]. Geophys J Int,197(1):443–457. doi: 10.1093/gji/ggt515
Tian X B,Zhang Z J. 2013. Bulk crustal properties in NE Tibet and their implications for deformation model[J]. Gondwana Res,24(2):548–559. doi: 10.1016/j.gr.2012.12.024
Zhang H J,Maceira M,Roux P,Thurber C. 2014. Joint inversion of body-wave arrival times and surface-wave dispersion for three-dimensional seismic structure around SAFOD[J]. Pure Appl Geophys,171(11):3013–3022. doi: 10.1007/s00024-014-0806-y
Zhang J H,Zheng T Y. 2015. Receiver function imaging with reconstructed wavefields from sparsely scattered stations[J]. Seismol Res Lett,86(1):165–172. doi: 10.1785/0220140028
Zhao Y,Guo L H,Guo Z,Chen Y J,Shi L,Li Y H. 2020. High resolution crustal model of SE Tibet from joint inversion of seismic P-wave travel-times and Bouguer gravity anomalies and its implication for the crustal channel flow[J]. Tectonophysics,792:228580. doi: 10.1016/j.tecto.2020.228580
Zhu L P,Kanamori H. 2000. Moho depth variation in southern California from teleseismic receiver functions[J]. J Geophys Res:Solid Earth,105(B2):2969–2980. doi: 10.1029/1999JB900322
-
期刊类型引用(3)
1. 高凯,刘宇实,师黎静. 基于近场记录的强震台站场地波速结构反演. 震灾防御技术. 2024(03): 436-445 .  百度学术
百度学术
2. Aowei HAO,Haijiang ZHANG,Shoucheng HAN,Wenliang XU. High-resolution Moho depth and V_p/V_s ratio distributions in northeast China from joint inversion of receiver functions and gravity data and their geological implications. Science China(Earth Sciences). 2023(07): 1569-1582 .  必应学术
必应学术
3. 郝奥伟,张海江,韩守诚,许文良. 接收函数和重力联合反演中国东北地区高精度莫霍面和波速比分布及地质意义. 中国科学:地球科学. 2023(07): 1586-1599 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: