Spatial autocorrelation method based on dense short-period seismic array and its application in the Guangdong-Hong Kong-Macao Greater Bay
-
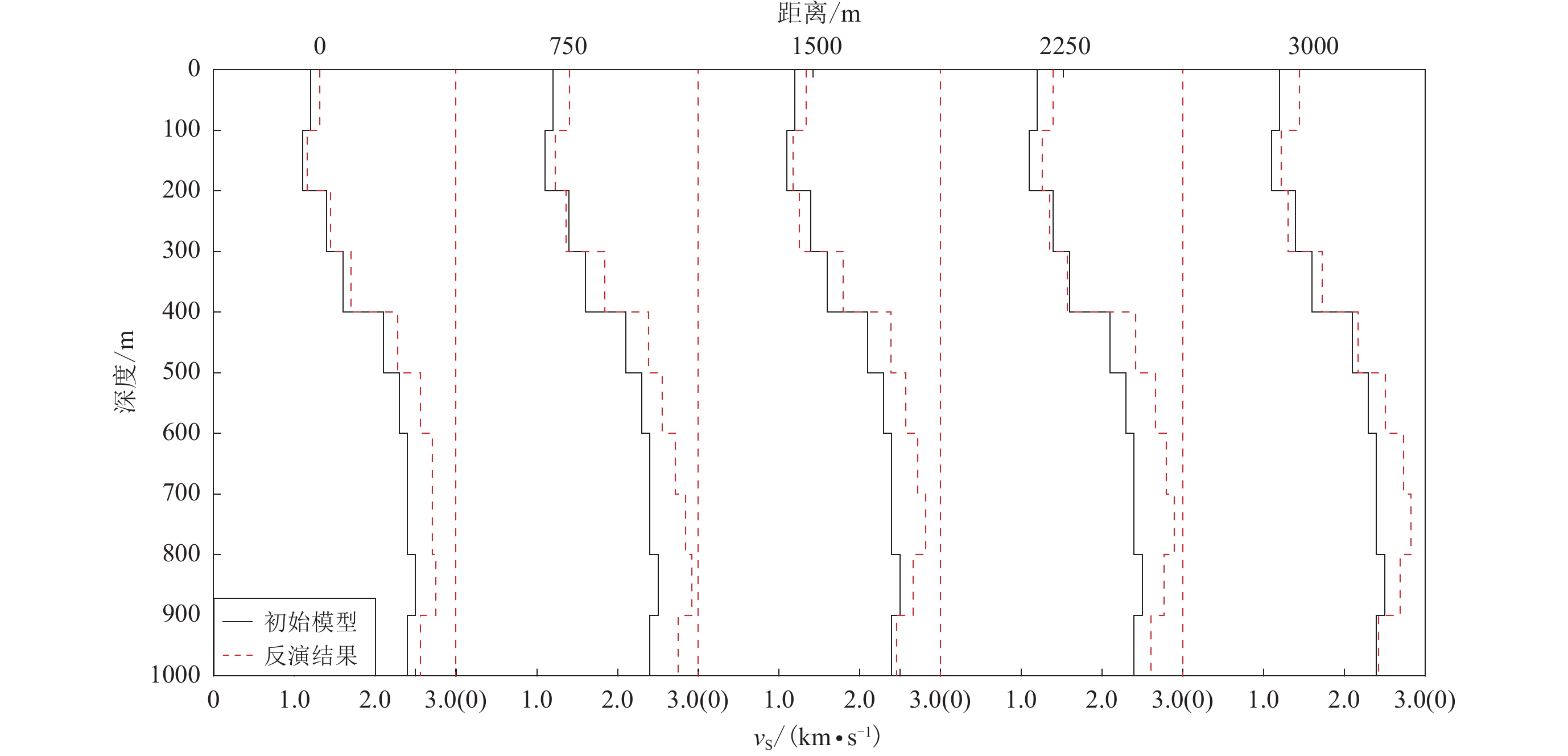
摘要: 基于空间自相关法从粤港澳大湾区短周期密集台阵的21个观测点记录的微动信号中提取了瑞雷波频散曲线，并反演得到了广州市番禺区内布设的台阵下方1 km深度范围内的浅层S波速度结构。结果显示：台阵下方0.25 km深度以内的速度明显偏低，介于1.17 km/s到1.59 km/s之间；0.25—1 km深度之间的速度平稳增加至2.88 km/s，表明通过空间自相关法可以有效地获取观测台阵下方稳定可靠的浅层速度结构。因此短周期密集台阵技术与空间自相关法结合是在人口稠密的城市群地区进行地下浅层的精细结构探测的一种有效、经济、环保的手段，将在未来城市地区的浅层结构探测中发挥重要作用。
-
关键词:
- 短周期密集台阵 /
- 空间自相关（SPAC）法 /
- 频散曲线 /
- S波速度结构
Abstract: Based on spatial autocorrelation （SPAC） method, the dispersion curves of Rayleigh wave have been extracted from the microtremor recorded by 21 stations belong to the dense short-period array deployed in Guangdong-Hong Kong-Macao Greater Bay area, and then the inversion for shallow S-wave velocity structures within a depth of 1 km beneath the Panyu district, Guangzhou city, have been performed. The results show that the velocity beneath the array is obviously low within 0.25 km depth, ranging from 1.17 km/s to 1.59 km/s, while the velocity increases steadily to 2.88 km/s between 0.25 km to 1 km depth. This indicates that the stability and the reliability of the method, which also implies that the SPAC is an effective, economical and environmental method for detecting the shallow fine structures in densely populated urban areas, and it will play an increasingly important role in the exploration of shallow structure in urban areas in the future. -
引言
地电场是地球固有的物理场，是地球电磁场的重要组成部分。地电场根据场源的不同分为大地电场和自然电场。大地电场与地球变化磁场及日月潮汐密切相关（傅承义等，1985；谭大诚等，2010）。自然电场主要分为过滤电场和扩散电场等，过滤电场是水在岩石孔隙中流动而形成的，扩散电场是由两种电荷浓度不同的溶液相接触而产生的（李金铭，2005）。在不同岩层接触面或岩石与溶液的接触面会形成双电层也会产生扩散电场（孙正江，王俊华，1984）。地电场在资源勘探、地质调查（李金铭，2005）、地震地质灾害事件的监测预测（Varotsos，Alexopoulos，1984；刘盛东等，2009；范莹莹等，2010；Uyeda，1998；安张辉等，2015；谭大诚等，2019）和地球电磁环境研究（Lanzerotti et al，2000；Pirjola，2005；汤吉等，2010； Ren et al，2015）方面得到了广泛应用。
我国从2000年开始进行规范化、规模化的地电场定点连续观测，在地电场的观测技术（王兰炜等，2011；席继楼等，2013）、变化特征（叶青等，2007；谭大诚等，2010；崔腾发等，2013）、形成机理（黄清华，刘涛，2006；张学民等，2007；谭大诚等，2010，2011）等方面作了大量研究，丰富了对地电场的认识。规范化、规模化的地电场连续观测，积累了大量观测数据，其中部分地电场具有气压非周期变化的形态。通过对气压的研究认为气压具有周期性的日变化特征以及周期几天至十几天不等的非周期变化特征，而后者则是气压变化能量分布的主要频段（罗少聪，2003）。本文利用宁夏地震局的四个地电台记录的地电场数据，在研究其变化特征、频谱特征、与区域气压变化关系及测量方向与附近断裂走向关系等的基础上，分析地电场气压非周期变化形态产生的机制。
1. 研究区域地质概况及观测概况
1.1 研究区域地质概况
固原、海原地电台坐落于海原断裂附近，海原断裂位于青藏高原东北缘，是中国大陆重要的活动地块边界断裂带之一（庞亚瑾等，2019），其西起甘肃景泰，经宁夏海原，东至固原，宽1—3 km，长240 km，由11条次级剪切断层组成。断裂走向在海原以西为280°—290°，海原以东为320° （国家地震局地质研究所，宁夏回族自治区地震局，1990）。根据断裂几何形态、地貌和活动习性，将海原断裂带分为西、中、东三段（Zhang et al，2005）。对海原断裂破碎带宽度的研究显示，海原断裂中段海原县西安州附近断裂破碎带宽度约为250 m （刘明军等，2004）。基于GPS和InSAR观测的研究结果认为海原断裂带西、中、东段闭锁深度各异，闭锁深度在数千米至数十千米不等（崔笃信等，2009；乔鑫等，2019）。海原地电台观测场地为干旱农田，周围地势开阔，距离海原断裂8 km；固原地电台观测场地为灌溉农田，周围地势开阔，距离海原断裂9 km；石嘴山地电台观测场地东边为北北东走向的贺兰山东麓断裂带（杜鹏，2010）；银川地电台东边为平罗—银川隐伏断裂，地表无出露，勘探结果显示平罗—银川隐伏断裂南段断层上断点埋深为11.8 m左右（柴炽章等，2011），银川地电台观测场地地下水位在地表以下3 m左右。
1.2 观测系统及观测方法
海原地电台有北南和东西两个正交测向，固原、银川地电台有北南、东西及北东三个测向，石嘴山地电台有北南、东西及北西三个测向，观测电极均为铅电极，海原、固原、银川地电台电极埋深为15 m，石嘴山地电台电极埋深为3 m，接地电阻均小于50 Ω。四个台站观测仪器为ZD8M地电阻率仪，电位测量分辨率为0.1 mV，测量频段为DC频段。图1为海原、固原地电台分布及布极图，A，B为供电电极，M，N为测量电极，供电电极A，B相距1 km，测量电极M，N相距200 m。本文研究的地电场由ZD8M测量的自然电位差除以测量极距得到。对观测电极的研究表明，同一观测场地相同测向，基于铅电极观测的地电场与基于固体不极化电极观测的地电场日变化形态相同，变化幅度接近，部分场地基于铅电极观测的地电场月变化呈现非周期变化现象（李学波，2022）。
![]()
图 1 海原、固原地电台站分布及布极图Figure 1. Distribution and electrodes layout of Haiyuan and Guyuan geoelectric station2. 固原、海原地电场的特征
2.1 固原、海原地电场的波形特征
图2左侧为2019年8月1日—10月30日海原和固原各测向的地电场整点值，右侧为2018年5月1—4日海原和固原各测向的地电场整点值。地电场日变幅度和稳定性受外界环境影响而变化，2019年8—10月、2018年5月1—4日地电场变化相对稳定。从图2可以看出，两个台站各测向地电场变化有以下特点：① 两个台站各测向地电场均有日变化特征，波峰波谷同步出现，且出现在午前午后，各测向地电场日变化大小有差异，日变幅在1—5 mV/km之间；② 两个台站各测向地电场没有月变化特征，月曲线形态有明显差异，其中海原北南向、固原北东向地电场为无序变化形态且变化幅度较大，海原北南向地电场月变化幅值接近15 mV/km，固原北东向地电场月变化幅值接近20 mV/km，两个台站其余测向月变化相对平稳，全月变化幅值明显较小。
![]()
图 2 海原（a）、固原（b）地电场变化特征左侧为月变化；右侧为日变化Figure 2. Variation characteristics of geoelectric field in Haiyuan （a） and Guyuan （b）Left column stands for monthly variations and right column stands for diurnal variations2.2 固原、海原地电场和气压的相关性
对海原北南向、固原北东向地电场的月曲线无序变化进行分析，结果表明两者形态相反，变化趋势相反，对两者一个月的数据进行相关性分析，无灌溉干扰的月份负相关系数达0.9 （观测现场测试两者负相关原因为仪器内部不同测量方向正、负向定义不同）。
将2019年10月海原北南向地电场、小山台钻孔应变北南向分量、气压及附近气温进行对比，结果如图3a所示，小山台与海原地电台相距11 km。将2019年10月固原北东向地电场、海子峡台体应变、气压及附近气温数据进行对比，结果如图3b所示，海子峡台与固原地电台相距13 km。从图中可以看出，海原北南向地电场变化形态与气压变化形态相反，固原北东向地电场变化形态与气压变化形态相似，海原北南向地电场和固原北东向地电场变化形态与气温变化形态不同，没有钻孔应变记录到的固体潮及趋势性变化特征。图4a，b分别为2019年10月海原和固原各测向地电场及气压整点值曲线。计算2018，2019年海原、固原地电场与气压整点值的月相关系数，结果列于表1；计算2018，2019年海原、固原地电场与气温整点值的月相关系数，结果列于表2。海原北南向、固原北东向地电场与气压的相关性较高（固原北东向地电场个别月份受灌溉影响，相关性较差），固原北南向、东西向地电场与气压相关性差，海原东西向地电场与气压不具有相关性。
![]()
图 3 2019年10月海原（a）和固原（b）北南向/北东向地电场、气压、钻孔应变及温度曲线Figure 3. Haiyuan （a） and Guyuan （b） north-south or north-east or geoelectric field，borehole strain，atmospheric pressure and temperature curves in October 2019![]()
图 4 2019年10月海原（a）、固原（b）地电场与气压整点值Figure 4. Hourly value of geoelectric field and atmospheric pressure in Haiyuan （a） and Guyuan （b） in October 2019表 1 海原和固原各测向地电场与气压的月相关系数Table 1. Monthly correlation coefficient between geoelectric field and atmospheric pressure in Haiyuan and Guyuan年-月 相关系数 年-月 相关系数 海原 固原 海原 固原 北南 东西 北南 东西 北东 北南 东西 北南 东西 北东 2018-01 −0.66 0.00 −0.36 −0.52 0.67 2019-01 −0.83 −0.11 −0.42 −0.63 0.75 2018-02 −0.77 0.12 −0.29 −0.07 0.64 2019-02 −0.76 −0.04 −0.22 −0.26 0.62 2018-03 −0.75 −0.21 −0.21 −0.62 0.52 2019-03 −0.73 −0.02 −0.27 −0.38 0.26 2018-04 −0.86 −0.16 −0.31 −0.56 0.19 2019-04 −0.71 −0.03 −0.25 −0.06 0.34 2018-05 −0.77 −0.19 −0.32 −0.59 0.57 2019-05 −0.83 0.23 −0.41 −0.54 0.42 2018-06 −0.76 0.10 −0.08 −0.46 −0.01 2019-06 −0.73 −0.07 −0.22 −0.21 0.46 2018-07 −0.58 −0.06 −0.30 −0.19 0.6 2019-07 −0.45 0.02 −0.06 −0.03 0.47 2018-08 −0.89 0.00 −0.35 −0.55 0.82 2019-08 −0.69 0.13 −0.02 −0.39 0.44 2018-09 −0.54 −0.05 −0.18 −0.65 −0.06 2019-09 −0.61 0.26 −0.14 −0.66 0.57 2018-10 −0.75 0.09 −0.24 −0.78 0.3 2019-10 −0.82 0.25 −0.33 −0.43 0.74 2018-11 −0.81 0.17 −0.41 −0.58 0.7 2019-11 −0.83 0.35 −0.61 −0.36 0.81 2018-12 −0.65 0.17 −0.43 −0.72 0.81 2019-12 −0.76 0.63 −0.50 −0.78 0.83 表 2 海原和固原各测向地电场与气温的月相关系数Table 2. Monthly correlation coefficient between geoelectric field and temperature in Haiyuan and Guyuan年-月 相关系数 年-月 相关系数 海原 固原 海原 固原 北南 东西 北南 东西 北东 北南 东西 北南 东西 北东 2018-01 0.46 0.15 0.20 0.39 −0.47 2019-01 0.35 0.25 0.30 0.27 −0.42 2018-02 0.48 −0.22 0.08 −0.28 −0.48 2019-02 0.35 −0.01 0.14 0.20 −0.24 2018-03 0.33 −0.21 0.11 −0.15 −0.33 2019-03 0.33 −0.17 −0.06 −0.27 −0.45 2018-04 0.50 −0.07 0.10 0.27 −0.06 2019-04 0.34 −0.06 0.00 −0.13 −0.46 2018-05 0.38 −0.15 −0.02 0.16 −0.42 2019-05 0.28 −0.01 0.03 0.05 −0.47 2018-06 0.09 −0.30 −0.22 0.20 −0.04 2019-06 0.12 −0.17 −0.25 −0.02 −0.48 2018-07 0.00 −0.27 0.09 −0.16 −0.23 2019-07 0.00 −0.23 0.13 0.27 −0.49 2018-08 0.17 −0.08 −0.22 0.25 −0.41 2019-08 0.34 −0.25 0.01 0.25 −0.50 2018-09 0.20 −0.01 −0.18 0.47 0.07 2019-09 0.32 −0.22 0.08 0.28 −0.51 2018-10 0.20 −0.04 0.03 0.01 −0.30 2019-10 0.23 −0.07 0.10 0.14 −0.52 2018-11 0.36 0.01 0.26 0.08 −0.50 2019-11 0.40 −0.07 0.22 0.47 −0.53 2018-12 0.52 −0.11 0.32 0.29 −0.57 2019-12 0.40 −0.10 0.29 0.06 −0.54 2.3 固原北东向、海原北南向地电场的年变化特征
图5为2018—2020年固原北东向和海原北南向地电场数据曲线，从图中可以看出，每年7—10月变化幅度较大。图6为2018—2020年海原北南向地电场、北南向浅层视电阻率、气压及温度曲线，从图中可以看出，海原北南向地电场7—10月变化与北南向视电阻率变化具有同步性，而气压在每年6—9月变化明显较小，与温度的变化具有同步性。可以看出在气压变化幅度较小的月份，地电场变化反而较大，可见这类地电场的年变化不是气压的年变化引起的。对2018—2020年海原北南向地电场的小时值作谱分析，如图7所示，可以看出其具有周期为365天的年变化特征和周期为半日的日变化特征。
![]()
图 5 2018—2020年海原北南向（左）和固原北东向（右）地电场Figure 5. Geoelectric field of Haiyuan north-south （left） and Guyuan north-east （right） from 2018 to 2020![]()
图 6 2018—2020年海原北南向地电场（a）、北南向浅层视电阻率（b）、温度（c）及气压（d）Figure 6. The north-south geoelectric field （a），north-south shallow apparent resistivity （b），temperature （c） and pressure （d） in Haiyuan from 2018 to 20203. 具有气压非周期变化形态的地电场产生机理分析
3.1 具有气压非周期变化形态的地电场变化与附近断裂的关系
由图4及表1可以看出海原北南向、固原北东向地电场有明显的气压非周期变化形态，与气压相关性较好，固原北南向、东西向地电场也与气压具有一定相关性。图8给出了石嘴山地电台和银川地电台的位置和布极图，以及两个地电台2019年10月各测向地电场及气压的整点值。此外本文还计算了2019年7月—12月石嘴山和银川地电台各测向地电场与气压的相关性，表3列出了2019年7—12月海原、固原、银川及石嘴山地电台各测向地电场与气压的月相关系数及各测向与附近断裂走向的夹角。
![]()
图 8 石嘴山地电台和银川地电台的分布（a）及其2019年10月各测向地电场与气压整点值（b）Figure 8. Distribution of Shizuishan and Yinchuan geoelectric station （a） and their hourly values of geoelectric field and atmospheric pressure in October 2019 （b）表 3 2019年7—12月海原、固原、银川和石嘴山电台各测向地电场与气压相关系数以及各测向与附近断裂走向的夹角Table 3. Correlation coefficients between geoelectric field and atmospheric pressure in Haiyuan，Guyuan，Shizuishan and Yinchuan geoelectric stations from July to December in 2019 and the angles between each measuring direction and the strike of nearby faults台站 测向 相关系数 夹角/° 7月 8月 9月 10月 11月 12月 平均值 海原 NS 0.45 0.69 0.61 0.82 0.83 0.76 0.69 70 EW 0.02 0.13 0.26 0.25 0.35 0.63 0.27 20 固原 NS 0.06 0.02 0.14 0.34 0.61 0.50 0.28 40 EW 0.03 0.39 0.66 0.44 0.36 0.78 0.44 50 NE 0.47 0.44 0.57 0.75 0.81 0.83 0.65 85 银川 NS 0.11 0.32 0.01 0.03 0.02 0.50 0.17 0 EW 0.13 0.37 0.67 0.21 0.19 0.47 0.34 90 NE 0.01 0.40 0.31 0.06 0.20 0.04 0.17 45 石嘴山 NS 0.25 0.25 0.51 0.10 0.30 0.43 0.31 15 EW 0.19 0.27 0.70 0.56 0.28 0.56 0.43 75 NW 0.12 0.68 0.66 0.43 0.53 0.61 0.51 60 分析海原、固原、银川、石嘴山四个地电台观测场地的主压应力方向（赵知军，刘秀景，1990；曾宪伟等，2015）、裂隙优势方位角及各测向与附近断裂的夹角（表4，图9）。可以看出在场地裂隙优势方位与附近断裂带方位呈近垂直或较大夹角时，与附近断裂走向近垂直测向的地电场与气压相关性较高，如海原北南向、固原北东向地电场；在场地裂隙优势方位与附近断裂带方位近平行时，各测向地电场与气压相关性不显著，如银川、石嘴山地电场。
表 4 各台站主压应力方向、裂隙优势方位角及各测向与附近断裂走向的夹角Table 4. Principal compressive stress direction and dominant fracture azimuth of each station and the angle between each measuring direction and the strike of nearby faults主压应力方向/° 裂隙优势方位角/° 附近断裂走向/° 地电场测向与附近断裂走向夹角/° NS EW NE 海原 60 71 290 70 20 固原 60 12 320 40 50 85 银川 42 16 0 0 90 45 石嘴山 26 28 15 15 75 60 （NW） ![]()
图 9 地电场测量方向、场地裂隙优势方位及附近断裂走向示意图Figure 9. Schematic diagram of geoelectric field measurement direction，dominant orientation of site fissures and nearby fault strike3.2 具有气压非周期变化形态的地电场形成的地球物理基础
断裂及两边渗透率不一致。Mizoguchi等（2008）对1995年日本神户地震野岛断层区出露的断层岩及周围岩石在180 MPa的各项同性围压条件下的渗透率进行了测量，结果显示野岛断层由低渗的断层泥（10−20—10−19 m2）、高渗的角砾岩破碎带（10−17—10−14 m2）及含裂隙的原岩（10−18—10−16 m2）组成。陈建业等（2011）对2008年汶川地震断层带进行了跨断层的渗透率测量，显示汶川地震断层由低渗的核部（10−19—10−16 m2）、高渗的破碎带（10−16—10−15 m2）以及含裂隙的原岩（10−18 m2）组成（有效压力40 MPa）。断层泥和两侧原岩由于渗透率低，阻碍流体跨断层带流动，破碎带则起到了流体通道的作用。这一结果与断层岩显微结构和粒度分布特征很好地吻合（来贵娟，2014）。
孙正江和王俊华（1984）计算了压力差导致裂隙水渗流产生的过滤电势差
$ \mathrm{\Delta }V $ ：$$ \mathrm{\Delta }V＝\frac{{\varepsilon }_{0}\varepsilon \rho \mathrm{\Delta }u}{\mu }\mathrm{\Delta }P \text{，} $$ (1) 式中，
$ \varepsilon $ 为水的介电常数，$ \;\rho $ 为水电阻率，$ \mathrm{\Delta }u $ 为水渗流的电偶极层电位跃变值，$ \mathrm{\Delta }P $ 为引起水渗流的压力梯度，$ \;\mu $ 为水的黏滞系数。地面上观测到的过滤电场与水渗流层的上下岩层性质有关。以层状介质为例，设上层介质电阻率为
$\; {\rho }_{1} $ ，厚度为$ {h}_{1} $ ；水渗流层的电阻率为$\; {\rho }_{2} $ ，厚度为$ {h}_{2} $ ；下层是不导电介质。在地面上观测到的电场强度E为（谭大诚等，2011）：$$ E＝\frac{\dfrac{{h}_{2}}{{\rho }_{2}}}{\dfrac{{h}_{2}}{{\rho }_{2}}＋\dfrac{{h}_{1}}{{\rho }_{1}}}\frac{{\varepsilon }_{0}\varepsilon \rho \mathrm{\Delta }u}{\mu }\mathrm{\Delta }P {\text{.}} $$ (2) 具有裂缝和孔隙双重储集空间和流动通道的介质称为双重介质。由于两种介质储集性能和渗透性能的不同，使得压力传播的速度不同，在空间的任意点同时引进两个压力，即裂缝中的压力和岩块的压力，和两个渗流速度，即裂缝的渗流速度和岩块的渗流速度，这样就形成了两个平行的渗流场，并且两个渗流场之间存在着流体交换，这种流体交换的物理现象称为“窜流”。
设裂缝系统和岩块系统的渗流均服从达西渗流定律，运动方程为（程林松，2011）：
$$ {v}_{{\rm{f}}}＝-\frac{{K}_{{\rm{f}}}}{\mu }\mathrm{\Delta }{P}_{{\rm{f}}} \text{，} $$ (3) $$ {v}_{{\rm{m}}}＝-\frac{{K}_{{\rm{m}}}}{\mu }\mathrm{\Delta }{P}_{{\rm{m}}} \text{，} $$ (4) 式中，
$ {v}_{{\rm{f}}}{\mathrm{和}v}_{{\rm{m}}} $ 分别为裂缝系统和岩块系统的渗流速度$ ，{K}_{{\rm{f}}} $ 和$ {K}_{{\rm{m}}} $ 分别为裂缝系统和岩块系统的渗透率，$ \mu $ 表示地下流体黏度，$ \mathrm{\Delta }{P}_{{\rm{f}}} $ 和$ \mathrm{\Delta }{P}_{{\rm{m}}} $ 分别为裂缝系统和岩块系统的压力梯度。3.3 具有气压非周期变化形态的地电场产生机理
将观测场地地下基岩和附近的断裂作为双重介质（图10）。在裂缝系统中，渗流速度与
$ \mathrm{\Delta }{P}_{{\rm{f}}} $ 直接关联，而$ \mathrm{\Delta }{P}_{{\rm{f}}} $ 值受大气压变化影响。式（5）表明在构成双重介质条件的观测场地上大气压变化会引起窜流速度$ {v}_{q} $ 的变化。![]()
图 10 含裂缝和孔隙的双重介质示意图（a）、剖面图（b）及地电场测量方向与断裂走向关系示意图（c）Figure 10. Schematic diagram of dual medium with fractures and pores （a），profile （b） and relationship between geoelectric field measuring direction and fault （c）$$ {v}_{{\rm{q}}}＝\frac{{K}_{{\rm{m}}}}{\mu }\mathrm{\Delta }{P}_{{\rm{m}}}－\frac{{K}_{{\rm{f}}}}{\mu }\mathrm{\Delta }{P}_{{\rm{f}}} {\text{.}} $$ (5) 地电场每日周期性变化的物理基础及机理比较清楚（徐文耀，李卫东，1993；黄清华，刘涛，2006；赵旭东等，2008；谭大诚等，2010，2011）。谭大诚等（2011）分析认为Sq电流在地表的感应电场导致的裂隙水电荷移动，其结果类似裂隙水的渗流。以层状介质为例，地表电场类似孙正江和王华俊（1984）计算的过滤电场。设上层介质电阻率为
$\; {\rho }_{1} $ ，厚度为$ {h}_{1} $ ；水渗流层的电阻率为$ \;{\rho }_{2} $ ，厚度为$ {h}_{2} $ ；下层是不导电介质。在地面上观测到的电场强度$ {E}_{2} $ 为（谭大诚，2011）：$$ {E}_{2}＝\frac{\dfrac{{h}_{2}}{{\rho }_{2}}}{\dfrac{{h}_{2}}{{\rho }_{2}}＋\dfrac{{h}_{1}}{{\rho }_{1}}}C\sum\limits _{i＝0}^{n}{v}_{{\rm{e}}i} \text{，} $$ (6) 式中，
${v}_{{\rm{e}}i}$ 为裂隙水的第i种电荷渗流速度，C为与流体电导率、介电常数及电荷体密度等相关的常数。所以，在构成双重介质条件观测场地上，有两个渗流场，一个为气压系统变化引起的渗流场，另外一个为空间Sq电流地面感应场引起的渗流场。在不同测量方向上渗流的驱动类型不同，地表观测到的电场也不一样。海原北南向、固原北东向观测到的电场主要是气压系统变化引起渗流而产生，空间Sq电流地面感应场引起渗流而产生的电场较弱；海原东西向观测到的电场是空间Sq电流地面感应场引起渗流而产生的；固原北南向、东西向观测到的电场主要是空间Sq电流地面感应场引起渗流而产生，气压系统变化引起渗流而产生的电场较弱。现场观测结果（空间Sq电流地面感应场产生的电场日变化幅度1—5 mV/km，气压系统变化引起渗流产生的电场变化幅度大于10 mV/km）与谭大诚等（2011）对中国大陆100多个台站地电场日变化研究的结论（感应电场使裂隙水渗流形成的大地电场峰-峰值多在5 mV/km，裂隙水周期性渗流产生的过滤电场峰-峰值多大于10 mV/km）相符合。
图8中银川、石嘴山台场地裂隙优势方位与附近断裂带方位近平行，各测向地电场与气压相关性不显著。而图6中在气压变化幅度较小的月份，地电场变化反而比其它月份大，并且地电场和相同测向视电阻率的变化具有同步性，说明这种现象与气压变化有关外，还与观测位置地下介质的电性有关，地下介质电阻率的年变化引起地电场的年变化。
综合上述讨论，认为具有气压非周期变化形态的地电场产生机理为：在构成双重介质条件观测场地上，在场地裂隙优势方位与附近断裂带方位呈近垂直或较大夹角时，与断裂走向近垂直测量方向上有两个不同驱动方式的渗流场，其中，空间Sq电流地面感应场引起的渗流是地表观测电场具有日变化形态的原因。气压系统变化引起的渗流是地表观测电场具有气压非周期变化形态的原因，变化大小与观测场地地下基岩孔隙渗透率、观测位置与断裂距离、测量方向与断裂走向夹角及观测位置地下介质的电性有关。
4. 结论
本文通过对宁夏四个地电台站基于铅电极观测的地电场进行研究，得出以下结论：
1） 气压是导致部分地电场变化的一种因素，部分地电场受气压影响具有气压非周期变化特征。
2） 具有气压非周期变化特征的地电场与气压非周期性变化为负相关，其相关程度与测量方向和附近断裂走向的夹角有关，在场地裂隙优势方位与附近断裂带方位呈近垂直或较大夹角时，与附近断裂走向近垂直测向的地电场与气压相关性较高；在场地裂隙优势方位与附近断裂带方位近平行时，各测向地电场与气压相关性不显著。
3） 研究认为地电场具有气压非周期变化特征与观测位置地下基岩的特性及附近断裂有关，是因为测量位置基岩孔隙的渗透率与附近断裂裂缝的渗透率不同，流体渗流过程中气压系统变化引起“窜流”而产生。
-
![]()
图 1 研究区短周期地震台站（倒三角形）分布示意图
Figure 1. Distribution of stations （denoted by inverse triangles） in the studied region
![]()
图 2 空间自相关法台阵（a）及不同台间距（b−f）下的台站对组合示意图
Figure 2. Schematic diagram of the SPAC subarray （a） and the combinations of stations with different station spacing （b−f）
![]()
图 3 原始微动记录（a）和预处理后的微动记录（b）
Figure 3. Raw records of the microtremors （a） and records of the microtremors after preprocessing （b）
![]()
图 4 五种台间距下的台站对的实测空间自相关系数ρ （a）以及平滑后的空间自相关系数ρ （b）
Figure 4. The SPAC coefficients ρ of the station-pairs with five different station distance （a） and corresponding coefficient ρ after smoothing （b）
![]()
图 5 根据空间自相关系数零极点计算得到的观测频散点及拟合频散曲线
Figure 5. The observed dispersion points calculated according to the zero-pole of SPAC coefficients and their polynomial fitting curve
![]()
图 6 初始模型和反演所得的S波速度结构（a）及观测频散点和反演的频散曲线（b）
Figure 6. Initial model and S-wave velocity structure from inversion （a） as well as the observed points and predicted dispersion curve （b）
![]()
图 7 按照台间距排列的S波速度结构（以第一个速度结构作为剖面线的起始点）
Figure 7. S-wave velocity structure sorted by station interval （Taking the first velocity structure as the initial point of the profile line）
![]()
图 8 S波速度结构（a）和标准差（b）（图中D为速度结构的距离）
Figure 8. Vertical sections of S-wave velocity obtained from different observation time periods （a） and standard deviation （b）（D represents the distance of the velocity structure）
表 1 研究区所用地震仪的主要性能指标
Table 1 Main parameters of the seismometers used in the studied region
地震仪 记录道数 ADC分辨率/bits 采样频率/ms 动态范围/dB 时间精度/μs SmartSolo IGU-16HR 3C 3 24 0.25，0.5，1，2，4，8，10，20 125 ±10，GPS驯服 Zland 3C 3 24 0.5，1，2，4 127 ±10，GPS驯服 
下载: 导出CSV
-
雷华,潘素珍,田晓峰,刘巧霞. 2019. 短周期密集台阵探测的应用进展[J]. 地质论评,65(增刊1):287–288. doi: 10.16509/j.georeview.2019.s1.135 Lei H,Pan S Z,Tian X F,Liu Q X. 2019. Recent application progress of short-period seismic dense array[J]. Geological Review,65(S1):287–288 (in Chinese).
刘庆华,鲁来玉,何正勤,胡刚,王凯明,龚艳. 2016. 地脉动空间自相关方法反演浅层S波速度结构[J]. 地震学报,38(1):86–95. doi: 10.11939/jass.2016.01.008 Liu Q H,Lu L Y,He Z Q,Hu G,Wang K M,Gong Y. 2016. Inversion of S-wave velocity structure near the surface by spatial autocorrelation technique of microtremors[J]. Acta Seismologica Sinica,38(1):86–95 (in Chinese).
裴文. 2011. 广州亚运城场区地层土性相关关系研究[D]. 广州: 华南理工大学: 35–37. Pei W. 2011. A Study of the Correlations Between Different Characteristic Index of Strata Soils in the Area of Asia Game Town, Guangzhou[D]. Guangzhou: South China University of Technology: 35–37 （in Chinese）.
任彦宗,卢占武,张新彦,薛帅,刘子龙,程永志,蔡玉国. 2021. 便携式节点地震仪数据采集和处理技术进展[J]. 地球物理学进展,36(2):779–791. doi: 10.6038/pg2021EE0097 Ren Y Z,Lu Z W,Zhang X Y,Xue S,Liu Z L,Cheng Y Z,Cai Y G. 2021. Progress in data acquisition and processing technology of portable node seismographs[J]. Progress in Geophysics,36(2):779–791 (in Chinese).
孙勇军,徐佩芬,凌甦群,李传金. 2009. 微动勘查方法及其研究进展[J]. 地球物理学进展,24(1):326–334. Sun Y J,Xu P F,Ling S Q,Li C J. 2009. Microtremor survey method and its progress[J]. Progress in Geophysics,24(1):326–334 (in Chinese).
王振东. 1990. 微动应用技术讲座(第一讲)[J]. 国外地质勘探技术,(4):12–16. Wang Z D. 1990. The lecture on microtremor application technology (chapter one)[J]. Foreign Geoexploration Technology,(4):12–16 (in Chinese).
徐佩芬,李传金,凌甦群,张胤彬,侯超,孙勇军. 2009. 利用微动勘察方法探测煤矿陷落柱[J]. 地球物理学报,52(7):1923–1930. doi: 10.3969/j.issn.0001-5733.2009.07.028 Xu P F,Li C J,Ling S Q,Zhang Y B,Hou C,Sun Y J. 2009. Mapping collapsed columns in coal mines utilizing microtremor survey methods[J]. Chinese Journal of Geophysics,52(7):1923–1930 (in Chinese).
徐佩芬,侍文,凌甦群,郭慧丽,李志华. 2012. 二维微动剖面探测“孤石”:以深圳地铁7号线为例[J]. 地球物理学报,55(6):2120–2128. doi: 10.6038/j.issn.0001-5733.2012.06.034 Xu P F,Shi W,Ling S Q,Guo H L,Li Z H. 2012. Mapping spherically weathered ‘Boulders’ using 2D microtremor profiling method:A case study along subway line 7 in Shenzhen[J]. Chinese Journal of Geophysics,55(6):2120–2128 (in Chinese).
Aki K. 1957. Space and time spectra of stationary stochastic waves,with special reference to microtremors[J]. Bull Earthq Res Inst,35(3):415–456.
Asten M W. 2006. On bias and noise in passive seismic data from finite circular array data processed using SPAC methods[J]. Geophysics,71(6):V153–V162. doi: 10.1190/1.2345054
Asten M W,Stephenson W J,Hartzell S. 2019. Spatially averaged coherencies (krSPAC) and Rayleigh effective-mode modeling of microtremor data from asymmetric arrays[J]. Geophysics,84(3):EN47–EN56. doi: 10.1190/geo2018-0524.1
Capon J. 1969. High-resolution frequency-wavenumber spectrum analysis[J]. Proc IEEE,57(8):1408–1418. doi: 10.1109/PROC.1969.7278
Herrmann R B, Ammon C J. 2002. Computer programs in seismology: Surface waves, receiver functions and crustal structure[CP/OL]. [2015-02-18]. http://www.eas.slu.edu/eqc/eqccps.html.
Li Z W,Ni S D,Zhang B L,Bao F,Zhang S Q,Deng Y,Yuen D A. 2016. Shallow magma chamber under the Wudalianchi Volcanic Field unveiled by seismic imaging with dense array[J]. Geophys Res Lett,43(10):4954–4961. doi: 10.1002/2016GL068895
Li Z W,Ni S D,Roecker S,Bao F,Wei X,Yuen D A. 2018. Seismic imaging of source region in the 1976 MS7.8 Tangshan earthquake sequence and its implications for the seismogenesis of intraplate earthquakes[J]. Bull Seismol Soc Am,108(3A):1302–1313. doi: 10.1785/0120170389
Lin F C,Li D Z,Clayton R W,Hollis D. 2013. High-resolution 3D shallow crustal structure in Long Beach,California:Application of ambient noise tomography on a dense seismic array[J]. Geophysics,78(4):Q45–Q56. doi: 10.1190/geo2012-0453.1
Okada H, Suto K. 2003. The Microtremor Survey Method[M]. Tulsa: Society of Exploration Geophysicists with the cooperation of Society of Exploration Geophysicists of Japan and Australian Society of Exploration Geophysicists: 40–45.
Okada H. 2006. Theory of efficient array observations of microtremors with special reference to the SPAC method[J]. Explor Geophys,37(1):73–85. doi: 10.1071/EG06073
Roux P,Moreau L,Lecointre A,Hillers G,Campillo M,Ben-Zion Y,Zigone D,Vernon F. 2016. A methodological approach towards high-resolution surface wave imaging of the San Jacinto fault zone using ambient-noise recordings at a spatially dense array[J]. Geophys J Int,206(2):980–992. doi: 10.1093/gji/ggw193
Savitzky A,Golay M J E. 1964. Smoothing and differentiation of data by simplified least squares procedures[J]. Anal Chem,36(8):1627–1639. doi: 10.1021/ac60214a047
Wei Y H,Tian X B,Duan Y H,Tian X F. 2018. Imaging the topography of crust-mantle boundary from a high-density seismic array beneath the middle-lower Yangtze River,eastern China[J]. Seismol Res Lett,89(5):1690–1697. doi: 10.1785/0220180045
Wessel P, Luis J F, Uieda L, Scharroo R, Wobbe F, Smith W H F, Tian D. 2019. The Generic Mapping Tools version 6[J]. Geochem Geophys Geosyst, 20（11）: 5556–5564.
Xia J H,Miller R D,Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics,64(3):691–700. doi: 10.1190/1.1444578
计量
- 文章访问数: 577
- HTML全文浏览量: 239
- PDF下载量: 154
