Dynamic adaptability of digital fringe processing for the laser interference absolute gravimeter and its shipboard applications evaluation
-
摘要: 激光干涉绝对重力仪干涉信号处理算法的动态适应性研究是进行动态绝对重力测量的基本前提。本文基于希尔伯特变换、直接正交法、过零点法三种瞬时相位处理算法，提出了基于背景振动物理量的合理动态约束条件，即反向的振动速度不能超过落体的下落速度。构建的单频振动信号仿真实验表明：在满足约束条件时，采样频率为60 MHz，希尔伯特变换算法的精度优于10−13 m/s2，过零点算法的精度优于10−9 m/s2，直接正交算法的精度为（−7.9±2.0）×10−8 m/s2。基于海浪模拟平台的实测试验表明：满足约束条件时，这三类瞬时相位处理算法均适用于动态环境，并获得了标准差为4.6×10−5 m/s2的绝对重力测量值。更进一步，基于本文动态适应性结论对系泊和海面船载动态环境进行评估，结果表明：测量船在3级以下海况可以进行10−5 m/s2量级绝对重力的测量；在3—4级海况下，需根据振动信号对测量结果进行筛选以获得10−5 m/s2量级绝对重力测量结果；4级以上海况则不适宜进行动态绝对重力测量。Abstract: The dynamic adaptability of digital fringe processing is a fundamental prerequisite for dynamic absolute gravity measurements. We have developed a dynamic restriction based on physical parameters of the background vibration according to the instantaneous phase methods, i.e., the reverse vibration velocity cannot exceed the falling velocity of the falling drop. This method involves the Hilbert transform, the direct quadrature, and the zero-crossing method. We have conducted simulation experiments with different vibration intensities and frequencies. The results show that this dynamic restriction is reasonable. The precision of the Hilbert transform method is better than 10−13 m/s2, the precision of the zero-crossing method is better than 10−9 m/s2, and the precision of the direct quadrature method is approximately （−7.9±2.0）×10−8 m/s2 at a 60 MHz sampling rate when the dynamic restriction is satisfied. Furthermore, we conducted absolute gravity measurements on a wave simulator, and obtained results with a standard deviation of 4.6×10−5 m/s2 . This verifies that the instantaneous phase methods apply to the dynamic environment when the restriction is satisfied. Based on the dynamic adaptability conclusion, we further evaluated the mooring system and the sea surface shipboard dynamic environment on the vessel. The evaluation revealed that the measurement vessel can conduct absolute gravity measurements with an accuracy of 10−5 m/s2 under sea conditions of grade 3 or below. Under sea conditions of grade 3−4, the measurement results need to be screened based on vibration signals to obtain absolute gravity measurements at the 10−5 m/s2 level. However, conducting dynamic absolute gravity measurements is not recommended under sea conditions above grade 4.
-
-
![]()
图 1 干涉信号、瞬时相位求解误差和瞬时频率的计算值的对应情况
Figure 1. The fringe signal and the phase’s instantaneous value error compared with the calculated instantaneous frequency
![]()
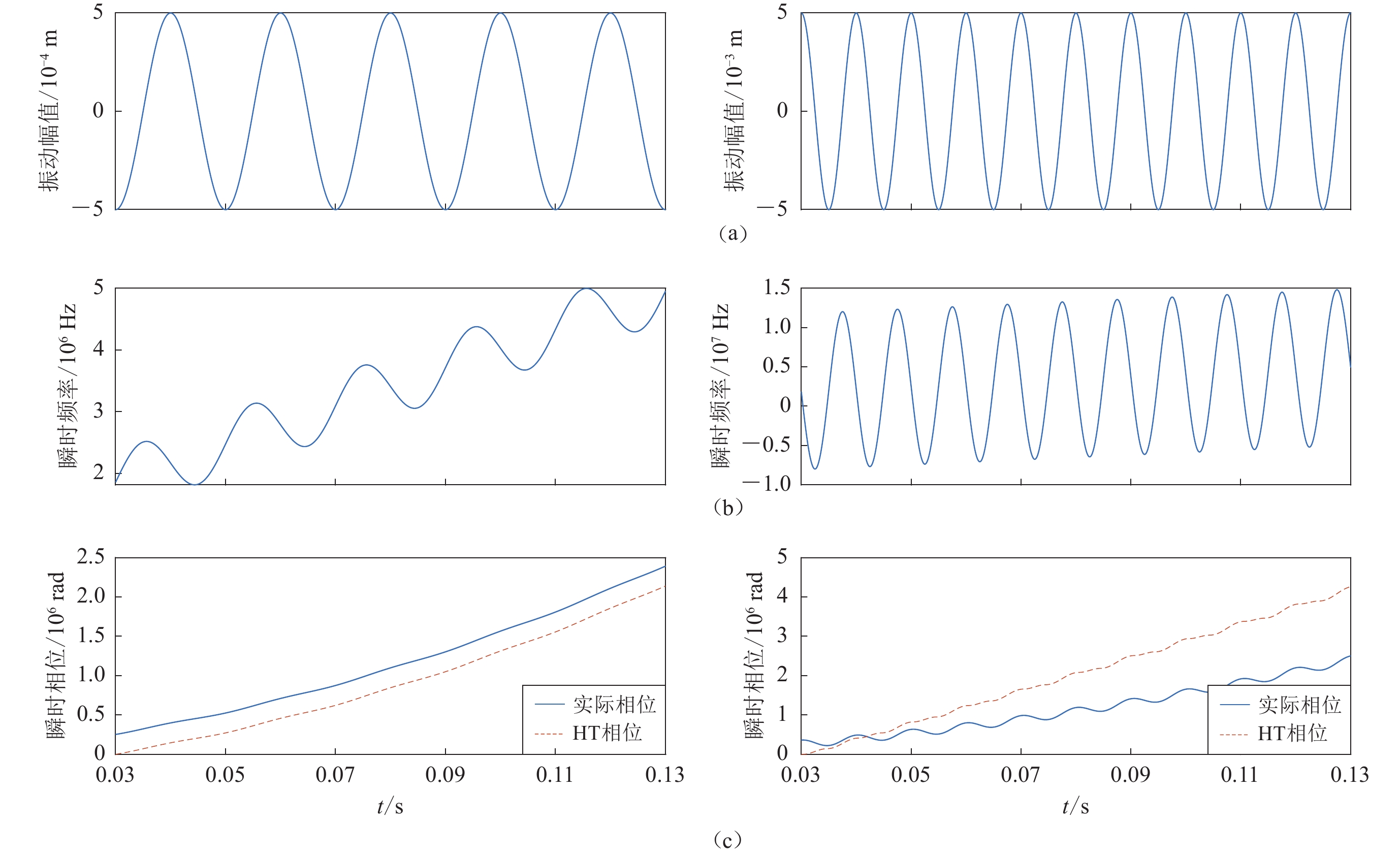
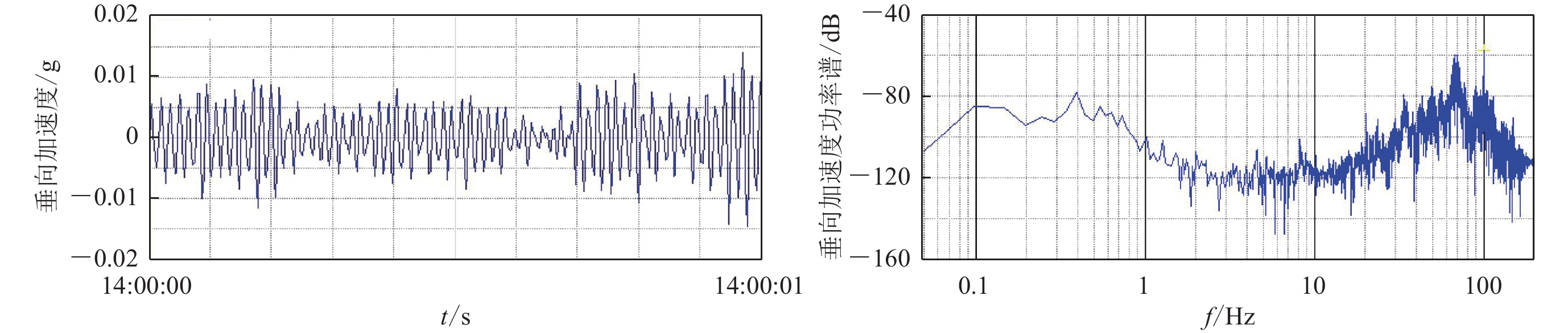
图 2 满足（左）和不满足（右）εω≤v0条件的振动信号对瞬时相位求解的影响
（a） 振动信号；（b） 计算出的干涉信号的瞬时频率；（c） 通过HT方法求解的瞬时相位与干涉信号的实际相位对比
Figure 2. The effect of whether the vibration signal satisfies the restrictions
（a）Vibration signal ；（b） Instantaneous frequency of the calculated interference signal；（c） Comparison of the instantaneous phase solved by the HT method with the actual phase of the interference signal
![]()
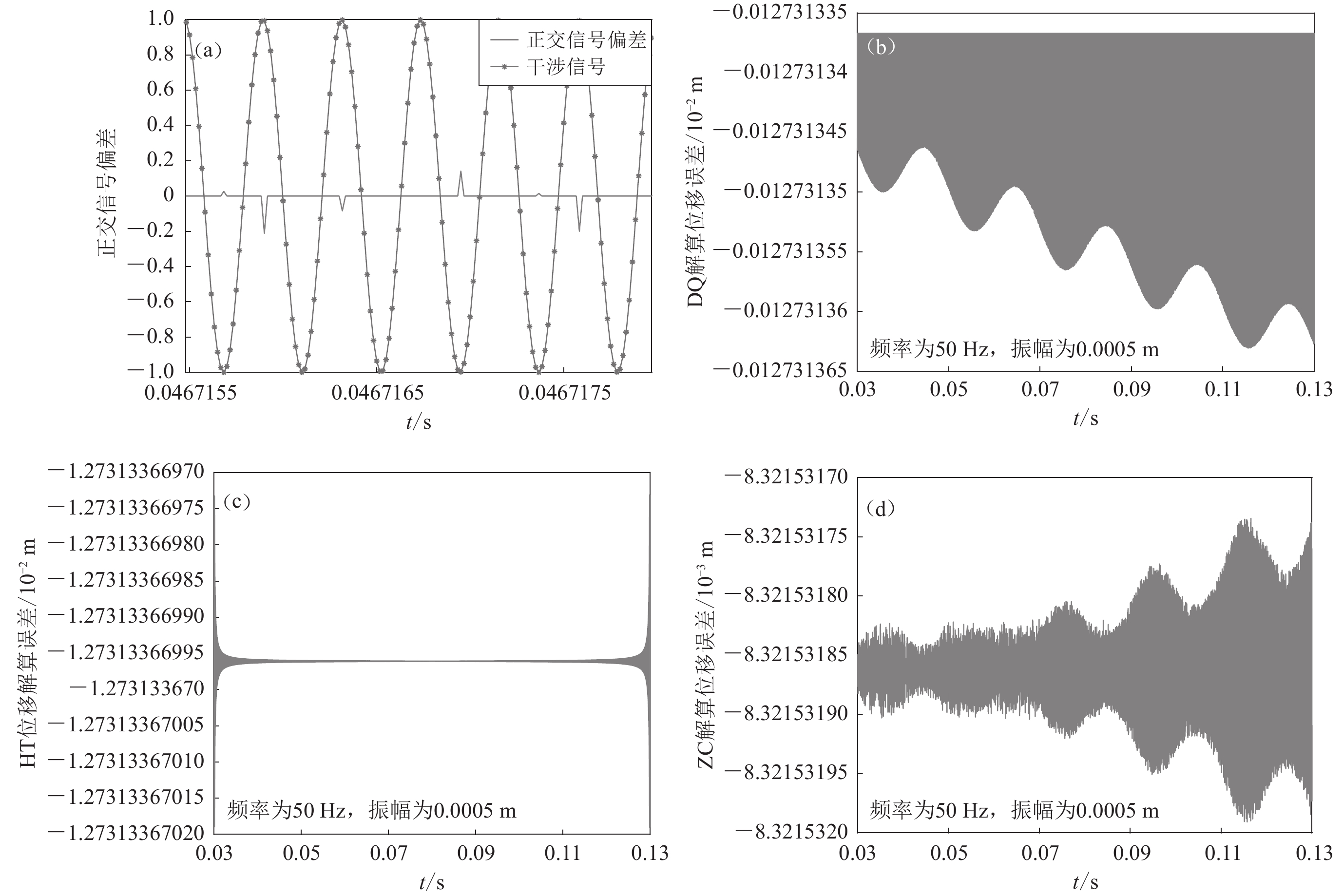
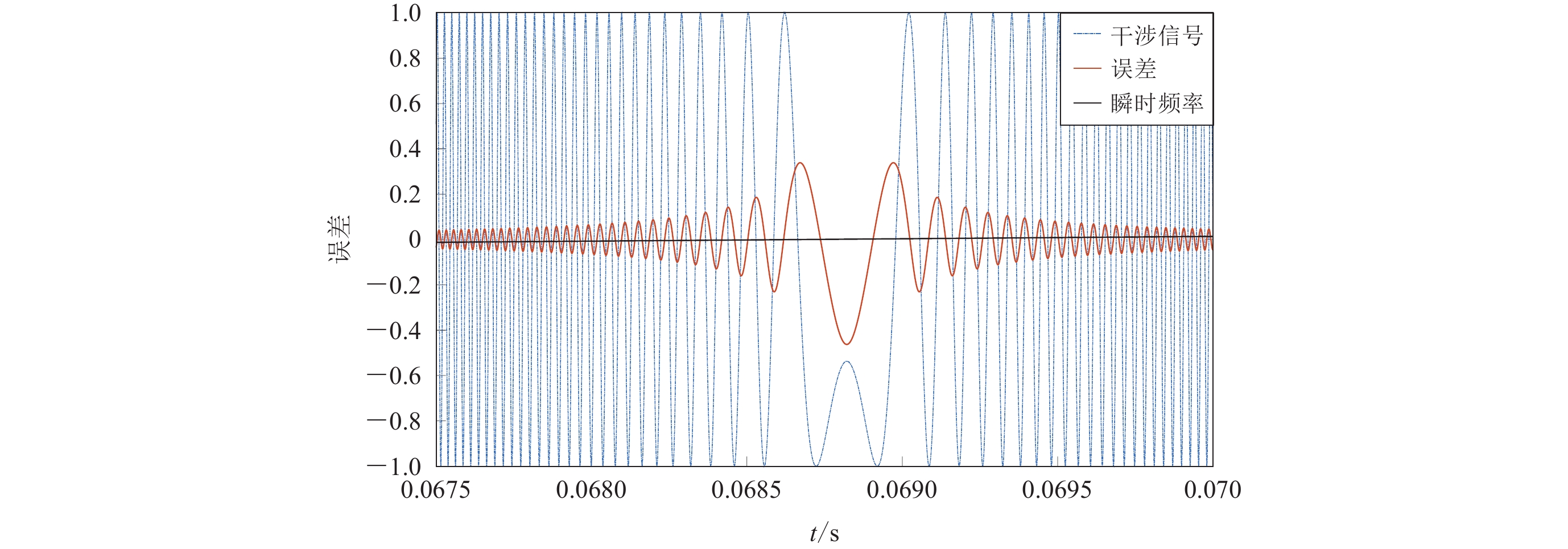
图 3 瞬时相位算法的误差分析
（a） DQ算法正交信号和仿真信号的正交信号之差与干涉信号的对比关系；（b—d）分别为单次下落中，DQ （b），HT （c）和ZC （d）算法位移与仿真信号的位移之差随时间的变化
Figure 3. Error analysis of the instantaneous phase methods
（a） the difference between the quadrature signal obtained by the DQ method and the ideal quadrature signal comparing with the fringe signal；（b）−（d） The deviation of the DQ， HT， ZC calculated displacement from the actual value
![]()
图 4 HT （a），DQ （b）和ZC （c）算法在不同采样频率下g的误差
Figure 4. g errors of HT （a），DQ （b） and ZC （c） methods at different sampling rates
![]()
图 5 单频振动信号实验
（a） 幅值和频率的乘积εω的归一化量级；（b—d） HT，DQ和ZC方法得到的重力值误差与振动信号的εω的对应关系
Figure 5. Single frequency vibration signal experiments
（a） εω，the product of amplitude and frequency of the vibration signal；（b−d） Errors of HT，DQ and ZC methods related to the εω of the vibration signal
![]()
图 6 海浪模拟平台试验装置（a）和模拟平台运动状态（b）（周期为17 s）
Figure 6. Sea wave simulator devices （a） and wave simulator movement （b） （the period is 17 s）
![]()
图 7 周期为17 s的海浪模拟平台试验结果
（a） 80个测量结果的直方图分布；（b） 以每组10个进行的分组测量的结果与均值间的偏差
Figure 7. Results of 17 s period wave simulator experiment
（a） Histogram distribution of 80 measurements，satisfies normal distribution；（b） Deviation of group measurements from the mean value for 10 units/group
![]()
图 8 船系泊时船体垂向加速度（a）及加速度信号功率谱（b）
Figure 8. The vertical acceleration （a） of the vessel during mooring，and the power spectrum （b） of the acceleration signal
![]()
图 9 船航行在时段1 （a）和时段2 （b）的垂荡位移
Figure 9. Raw ship heave data on sailing at the period 1 （a） and period 2 （b）
![]()
图 10 3—4级海况下连续100次测量的HT，DQ和ZC瞬时相位算法误差及船的垂荡速度
Figure 10. Errors of HT，DQ and ZC methods for 100 consecutive measurements at level 3−4 sea state and the vertical velocity of the vessel
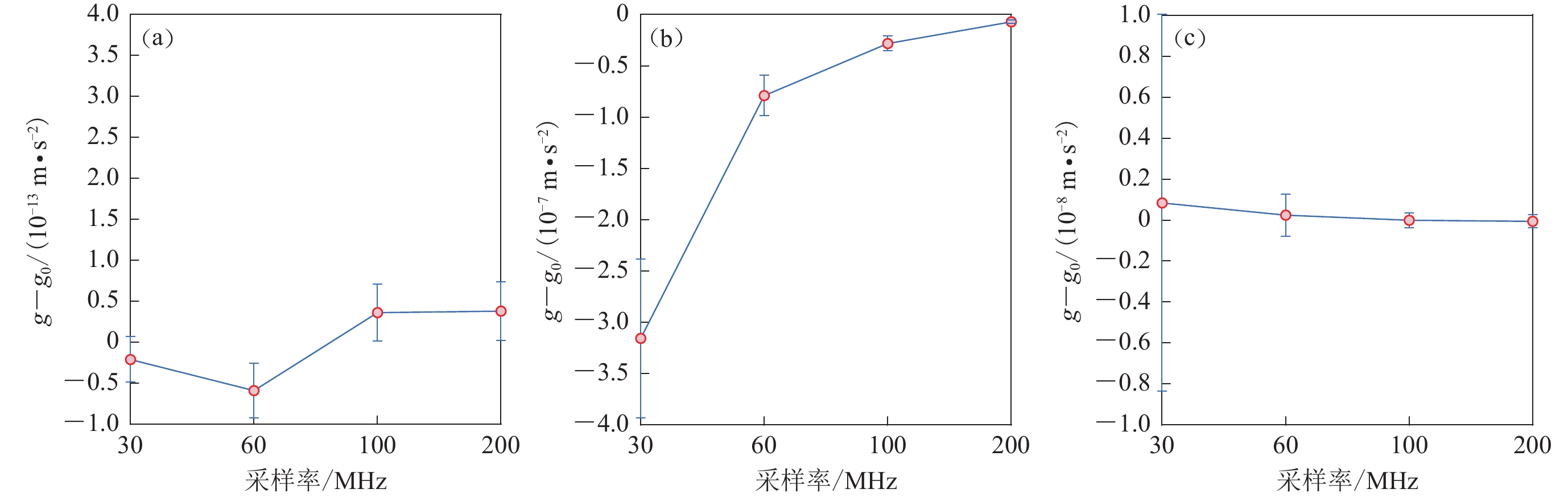
表 1 不同方法的瞬时相位误差
Table 1 Errors in the instantaneous phase methods
方法 g－g0 误差/ m·s−2 εω≤v0 εω$\gg $v0 HT （−5.9±3.3）×10−14 绝对值＞1 DQ （−7.9±2.0）×10−8 绝对值＞1 ZC （2.4±1.0）×10−10 绝对值＞1 
下载: 导出CSV
表 2 船系泊状态下g值的偏差和标准差
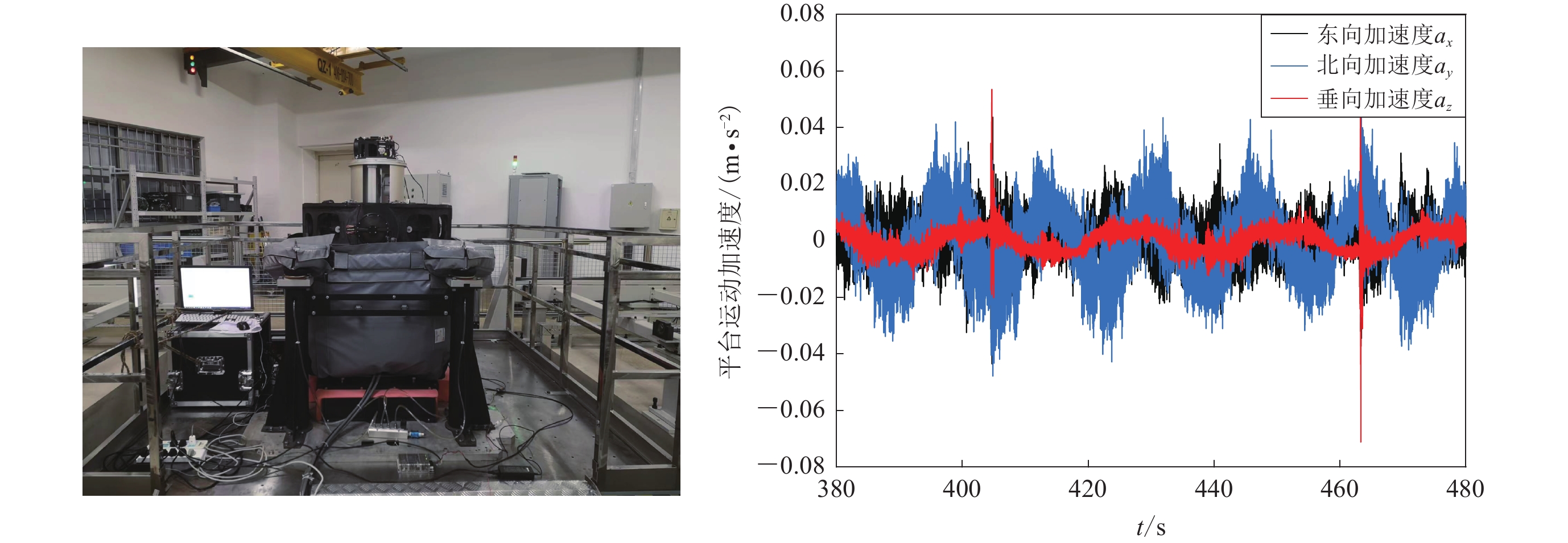
Table 2 The bias of the average g and the standard deviations of g at vessel mooring
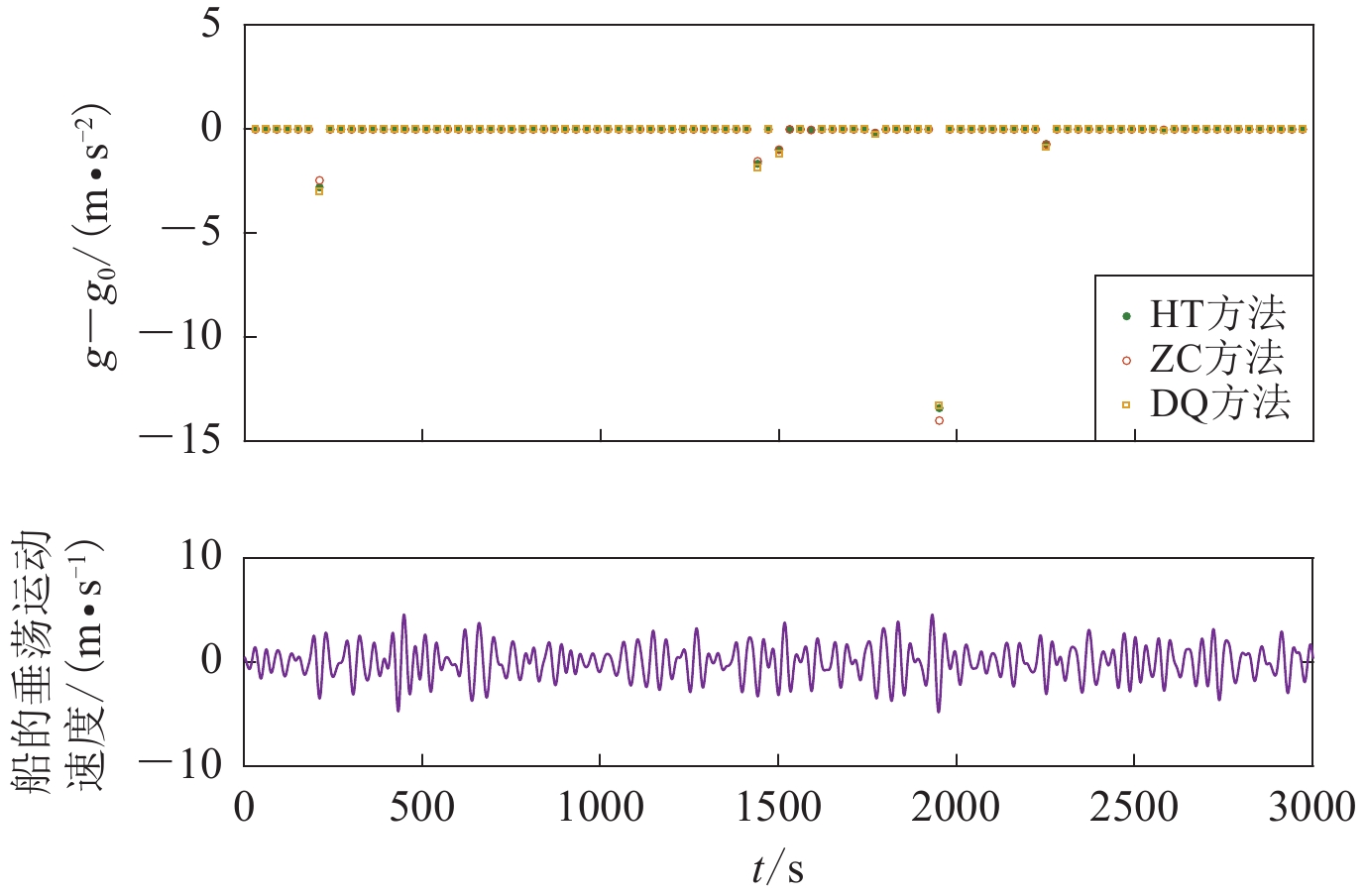
方法 g与g0 偏差/（m·s−2） 标准差/（m·s−2） HT −8.2×10−15 3.1×10−13 DQ −8.4×10−8 2.7×10−7 ZC 1.5×10−10 1.2×10−7
下载: 导出CSV
表 3 船航行状态下g值的偏差和标准差（单位：10−8 m·s−2）
Table 3 The bias of the average g and the standard deviations of g on ship sailing state （unit：10−8 m·s−2）
HT方法 DQ方法 ZC方法 g－g0 误差 标准差 g－g0误差 标准差 g－g0 误差 标准差 时段1 −9.0×10−7 3.5×10−6 −8.4 0.24 1.1×10−2 9.4×10−2 时段2（全） ＞ 108 ＞ 108 ＞ 108 时段2（筛选） −1.5×10−6 4.2×10−6 −8.4 0.27 1.8×10−2 0.18
下载: 导出CSV
-
高景龙. 1993. NIM-3型新的轻小高精度可移式绝对重力仪[J]. 测绘学报,22(3):223–229. Gao J L. 1993. A new type NIM-3 transportable absolute gravimeter of small size and light weight[J]. Acta Geodaetica et Cartographica Sinica,22(3):223–229 (in Chinese).
胡华,伍康,申磊,李刚,王力军. 2012. 新型高精度绝对重力仪[J]. 物理学报,61(9):099101. Hu H,Wu K,Shen L,Li G,Wang L J. 2012. A new high precision absolute gravimeter[J]. Acta Physica Sinica,61(9):099101 (in Chinese). doi: 10.7498/aps.61.099101
刘敏,黄谟涛,欧阳永忠,邓凯亮,翟国君,陆秀平,吴太旗,陈欣. 2017a. 海空重力测量及应用技术研究进展与展望(一):目的意义与技术体系[J]. 海洋测绘,37(2):1–5. Liu M,Huang M T,Ouyang Y Z,Deng K L,Zhai G J,Lu X P,Wu T Q,Chen X. 2017a. Development and prospect of air-sea gravity survey and its applications,part Ⅰ:Objective,significance and technical system[J]. Hydrographic Surveying and Charting,37(2):1–5 (in Chinese).
刘敏,黄谟涛,欧阳永忠,邓凯亮,翟国君,陆秀平,吴太旗,陈欣. 2017b. 海空重力测量及应用技术研究进展与展望(二):传感器与测量规划设计技术[J]. 海洋测绘,37(3):1–11. Liu M,Huang M T,Ouyang Y Z,Deng K L,Zhai G J,Lu X P,Wu T Q,Chen X. 2017b. Development and prospect of air-sea gravity survey and its applications,part Ⅱ:Sensor,plan and design of survey[J]. Hydrographic Surveying and Charting,37(3):1–11 (in Chinese).
孙和平,孙文科,申文斌,申重阳,祝意青,付广裕,吴书清,崔小明,陈晓东. 2021. 地球重力场及其地学应用研究进展:2020中国地球科学联合学术年会专题综述[J]. 地球科学进展,36(5):445–460. Sun H P,Sun W K,Shen W B,Shen C Y,Zhu Y Q,Fu G Y,Wu S Q,Cui X M,Chen X D. 2021. Research progress of Earth's gravity field and its application in geosciences:A summary of Annual Meeting of Chinese Geoscience Union in 2020[J]. Advances in Earth Science,36(5):445–460 (in Chinese).
滕云田,吴琼,郭有光,张兵,张涛. 2013. 基于激光干涉的新型高精度绝对重力仪[J]. 地球物理学进展,28(4):2141–2147. doi: 10.6038/pg20130459 Teng Y T,Wu Q,Guo Y G,Zhang B,Zhang T. 2013. New type of high-precision absolute gravimeter base on laser interference[J]. Progress in Geophysics,28(4):2141–2147 (in Chinese).
吴彬,周寅,程冰,朱栋,王凯楠,朱欣欣,陈佩军,翁堪兴,杨秋海,林佳宏,张凯军,王河林,林强. 2020. 基于原子重力仪的车载静态绝对重力测量[J]. 物理学报,69(6):060302. doi: 10.7498/aps.69.20191765 Wu B,Zhou Y,Cheng B,Zhu D,Wang K N,Zhu X X,Chen P J,Weng K X,Yang Q H,Lin J H,Zhang K J,Wang H L,Lin Q. 2020. Static measurement of absolute gravity in truck based on atomic gravimeter[J]. Acta Physica Sinica,69(6):060302 (in Chinese).
吴琼. 2011. 高精度绝对重力仪关键技术研究[D]. 北京: 中国地震局地球物理研究所: 82–92. Wu Q. 2011. The Study of the Key Technology in High-Precision Absolute Gravimeter[D]. Beijing: Institute of Geophysics, China Earthquake Administration: 82–92 （in Chinese）.
吴燕雄,滕云田,吴琼,徐行,张兵. 2022. 船载绝对重力仪测量系统的误差修正模型及不确定度分析[J]. 武汉大学学报•信息科学版,47(4):492–500. Wu Y X,Teng Y T,Wu Q,Xu X,Zhang B. 2022. Error correction model and uncertainty analysis of the shipborne absolute gravity measurement system[J]. Geomatics and Information Science of Wuhan University,47(4):492–500 (in Chinese).
肖凡. 2012. FG5高精度绝对重力测量影响因素研究[D]. 郑州: 中国人民解放军信息工程大学: 25–28. Xiao F. 2012. Research on the Effect Factors for the High Precision Absolute Gravity Surveying Using FG5[D]. Zhengzhou: PLA Information Engineering University: 25–28 （in Chinese）.
Baumann H,Klingelé E E,Marson I. 2012. Absolute airborne gravimetry:A feasibility study[J]. Geophys Prospect,60(2):361–372. doi: 10.1111/j.1365-2478.2011.00987.x
Bedrosian E. 1963. A product theorem for Hilbert transforms[J]. Proc IEEE,51(5):868–869.
Bidel Y,Zahzam N,Blanchard C,Bonnin A,Cadoret M,Bresson A,Rouxel D,Lequentrec-Lalancette M F. 2018. Absolute marine gravimetry with matter-wave interferometry[J]. Nat Commun,9(1):627. doi: 10.1038/s41467-018-03040-2
Bidel Y,Zahzam N,Bresson A,Blanchard C,Cadoret M,Olesen A V,Forsberg R. 2020. Absolute airborne gravimetry with a cold atom sensor[J]. J Geod,94:20. doi: 10.1007/s00190-020-01350-2
Brown J M, Niebauer T M, Klingele E. 2001. Towards a dynamic absolute gravity system[C]//Gravity, Geoid and Geodynamics 2000. Banff, Alberta, Canada: Springer: 223–228.
Huang N E,Shen Z,Long S R,Wu M C,Shih H H,Zheng Q A,Yen N C,Tung C C,Liu H H. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc Roy Soc A:Math Phys Eng Sci,454(1971):903–995. doi: 10.1098/rspa.1998.0193
Huang N E,Wu Z H,Long S R,Arnold K C,Chen X Y,Blank K. 2009. On instantaneous frequency[J]. Adv Adapt Data Anal,1(2):177–229. doi: 10.1142/S1793536909000096
Merlet S, Le Gouët J, Bodart Q, Clairon A, Landragin A, Dos Santos F P, Rouchon P. 2010. Vibration rejection on atomic gravimeter signal using a seismometer[C]//Gravity, Geoid and Earth Observation. Chania, Crete, Greece: Springer: 115–121.
Niebauer T M,Sasagawa G S,Faller J E,Hilt R,Klopping F. 1995. A new generation of absolute gravimeters[J]. Metrologia,32(3):159–180. doi: 10.1088/0026-1394/32/3/004
Nuttall A H,Bedrosian E. 1966. On the quadrature approximation to the Hilbert transform of modulated signals[J]. Proc IEEE,54(10):1458–1459. doi: 10.1109/PROC.1966.5138
Sandwell D T,Müller R D,Smith W H F,Garcia E,Francis R. 2014. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure[J]. Science,346(6205):65–67. doi: 10.1126/science.1258213
Sokolov A V,Krasnov A A,Konovalov A B. 2016. Measurements of the acceleration of gravity on board of various kinds of aircraft[J]. Meas Tech,59(6):565–570. doi: 10.1007/s11018-016-1009-y
Svitlov S,Rothleitner C,Wang L J. 2012. Accuracy assessment of the two-sample zero-crossing detection in a sinusoidal signal[J]. Metrologia,49(4):413–424. doi: 10.1088/0026-1394/49/4/413
Svitlov S,Araya A. 2014. Homodyne interferometry with quadrature fringe detection for absolute gravimeter[J]. Appl Opt,53(16):3548–3555. doi: 10.1364/AO.53.003548
Verdun J,Bayer R,Klingelé E E,Cocard M,Geiger A,Halliday M E. 2002. Airborne gravity measurements over mountainous areas by using a LaCoste & Romberg air-sea gravity meter[J]. Geophysics,67(3):807–816. doi: 10.1190/1.1484525
计量
- 文章访问数: 130
- HTML全文浏览量: 68
- PDF下载量: 37
