The magnitude of the Sanhe-Pinggu earthquake based on the multi-rupture method
-
摘要:
在前人对三河—平谷地震研究的基础上,本文采用多震级、多破裂方式对三河—平谷地区进行地震动模拟,以开展三河—平谷地震的震级研究。首先,我们将研究区域的历史烈度曲线转化为峰值加速度(PGA)和峰值速度(PGV),随后将其与多震级、多破裂方式下的模拟结果进行对比。通过分析差异值,初步确定最贴近三河—平谷地震震级的三个可能值,分别为MW7.8,MW7.9和MW8.0。进一步比较这三个震级下的180种破裂模式及其产生的烈度空间分布形态与历史烈度形态的相似度,筛选出四种最相符的破裂模式。将这四种模式生成的烈度曲线与历史烈度进行对比,最终得出夏垫断裂在三河—平谷地区巨震的实际震级。研究结果显示,该震级小于人们通常认知的MW8.0,更趋近于MW7.9−或MW7.8++。
Abstract:The 1679 Sanhe-Pinggu earthquake is the largest earthquake ever recorded in the history of the Beijing-Tianjin-Hebei region, causing severe damage. But the surface rupture length and related deformation characteristics from a series of studies do not match the defined MW8.0. Therefore, this article, building upon previous research, simulates the strong ground motion of the Sanhe-Pinggu earthquake using the multi-rupture and multi-focal set method, aiming to study its magnitude and ultimately determine the true magnitude of the Sanhe-Pinggu earthquake. The method employed in this paper is the NNSIM (non-negative source-specific impulse modeling) random finite fault method, drawing inspiration from traditional random finite fault methods. It divides the main fault into N sub-faults that can be considered as point sources. Under the influence of rupture delay and propagation delay, the simulation results for each sub-fault are superimposed to obtain the seismic effects of the entire fault. The paper also provides a detailed explanation of the role of time window functions in the low-frequency domain. In this approach, we use this method to make the low-frequency component of the simulated seismic effects closer to the actual records, thereby enhancing the reliability of the simulation results across the entire frequency spectrum. The Sanhe-Pinggu earthquake occurred on the Xiaodian fault. Building upon previous research, we selected the middle section of the Xiadian Fault as the study area, with a total length of approximately 80 km and a width of 25 km. We divided the magnitude range from MW7.5 to MW8.0 into six magnitude levels with an increment of 0.1, and each magnitude level was simulated using multiple source and multiple rupture scenarios.Considering that the Sanhe-Pinggu earthquake is a historically significant event in the North China region, we incorporated two fault asperities in our simulation. According to our setup criteria and the distribution of slip for each rupture mode, we calculated corresponding stress drop distributions, rupture velocity distributions, rise time distributions, and different source functions, which can generate complex earthquake source models. Our calculations revealed that there are primarily two rupture points along the fault, one at around 20 km and the other at around 60 km, with the rupture at 20 km being more intense. The initial rupture times for the fault are concentrated between 0.02 s and 0.05 s, with a maximum duration of up to 22 s. The resulting seismic moment is approximately 7×1025 N·m, and the maximum stress drop occurs near 8 MPa. These four distributions represent the seismic source parameters required for the NNSIM simulation method used in this study. Based on these seismic source parameters, we conducted simulations of strong ground motions under multiple rupture scenarios. In order to determine the magnitude of the Sanhe-Pinggu earthquake, we first converted the historical intensity curves Ⅸ, Ⅹ, and Ⅺ into peak ground acceleration (PGA) and peak ground velocity (PGV) values according to GB/T 17742−2020 (Chinese Seismic Intensity Scale). Specifically, intensity Ⅸ corresponds to 402 cm/s2, intensity Ⅹ corresponds to 831 cm/s2, and intensity Ⅺ corresponds to 1730 cm/s2. Each intensity curve was sampled at approximately 50 points. Based on the principle that the maximum fault asperity is located southwest of the macroscopic epicenter, we constrained the position of the maximum fault asperity to be in the southwest of the macroscopic epicenter. Through calculations in the seismic source setup section, we identified a total of 180 rupture scenarios that satisfied this constraint. We then used the NNSIM method to compute the acceleration, velocity, PGA, and PGV values at comparison reference points. By evaluating the differences between the simulated and converted PGA and PGV values, we defined two parameters, R and S, to reflect the disparities between the acceleration, velocity, PGA, and PGV at reference points and historical intensity values.From these differences, it was determined that the simulated PGA and PGV values for MW7.8 exhibited the smallest discrepancies with historical intensity values, followed by MW7.9, while MW8.0 showed relatively larger discrepancies. For the purpose of conducting a detailed comparative analysis of the spatial distribution of simulated ground motion for earthquakes with magnitudes MW7.8, MW7.9, and MW8.0, we utilized 180 different rupture scenarios corresponding to these three magnitudes. We simulated strong ground motions for each of these scenarios and plotted intensity curves corresponding to intensities Ⅸ, Ⅹ, and Ⅺ.From the four intensity curves for MW7.8, it can be observed that the Ⅸ and Ⅹ intensity curves closely matched historical intensity curves. However, the MW7.8 scenarios almost did not generate Ⅺ intensity, indicating that within the seismogenic area, MW7.8 is insufficient to produce ground motions with a PGA exceeding 1730 cm/s2. For the MW7.9 earthquake, the Ⅸ and Ⅹ intensity ranges exceeded the corresponding historical intensity circles, while the spatial range of the Ⅺ intensity circle closely resembled that of the historical intensity circle, but it was slightly shifted to the south.In the case of the MW8.0 earthquake, the intensity ranges for all three intensities were much larger than the historical intensity circles. The Ⅺ and Ⅹ intensities were similar in size to historical Ⅹ and Ⅸ intensities, but the Ⅸ intensity extended far beyond the historical Ⅸ intensity range. This suggests that the rupture generated by the MW8.0 earthquake is significantly more powerful than what historical records indicate. In conclusion, the magnitude of the Sanhe-Pinggu earthquake should be less than MW8.0, greater than MW7.8, and close to MW7.9. It is likely to be an earthquake with a magnitude around MW7.8+ + or even MW7.9−.
-
Keywords:
- magnitude research /
- multi-rupture method /
- multi-focal set /
- Sanhe-Pinggu earthquake
-
引言
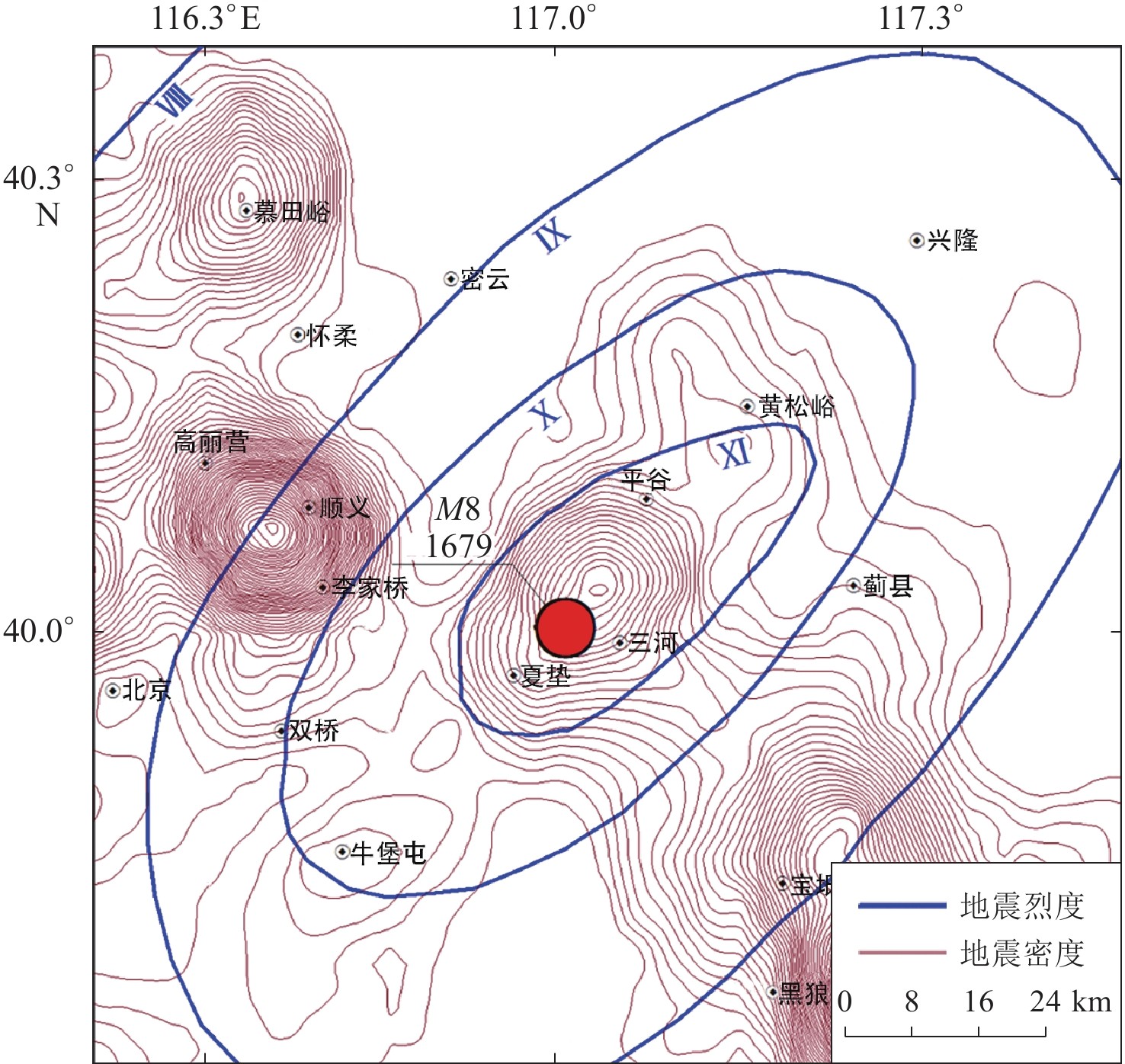
1679年发生的三河平谷M8大地震是目前首都圈有记录的震级最大的地表破裂型地振动,地震震中烈度高达Ⅺ级。其震中位置位于河北省夏垫镇,震源方位为38.23°,倾角为82.54°,滑动角为−156.08°,地震产生的断裂断层从东流河屯附近开始,向东蔓延穿过夏垫镇北部,一直到东兴庄附近,地震极震区面积达1 800 km2,影响到整个华北地区,造成了巨大的人民生命与财产损失。其中破坏最严重的是三河、平谷地区,余震也波及到房山、延庆、昌黎、定县、新城、天津等20余县市(彭一民等,1981;向宏发等,1988;徐锡伟等,2000;刘保金等,2009;Wang et al,2014)。
地震区的地质构造情况也是构建地震模型的重要部分(Borcherdt,1991),近年来,三河—平谷的地震构造也成为许多研究的主题。地质结构研究表明,三河—平谷地震发生在北京东部的华北俯冲带与燕山隆起带交会的平原,存在断裂带的复合,地质构造和沉积形态复杂,呈现出强烈的新构造运动,并且在此地区附近小震活动频繁,地震震中呈带状分布,震源深度通常比较浅(田优平等,2014)。三河—平谷地震的发震断层上因有新生代沉积覆盖,不能完全在地表出露,这可能是造成此次地震震级较大的原因之一(彭菲等,2020)。震区上地壳存在部分不连续,倾斜不一致的反射叠层,展示出了此处地质构造的复杂性。从剖面表现出的特征来看,此处断裂构造体系存在有规律的脆-韧转换,容易积累应变,从而导致地震发生(刘保金等,2009)。
前人对京津唐地区地壳结构与强震发生关系的研究表明,三河—平谷地震与唐山地震有着非常相似的构造背景,均发生在速度变化较快的位置(孙若昧等,1993;张先康等,2002;于湘伟等,2010)。Huang等(2021)提出的拟波形地震层析方法基于北京及周边地区的多个高精度宽频数字地震台站所积累的丰富的高精度地震资料,利用数值求解波动方程反演了首都圈地区地壳的三维纵波、横波速度和泊松比结构,得出这两次大地震的震源区域有很大的相似性,为上述结论提供了新的证据。张先康等(2002)的研究表明,三河—平谷震区位于一个横波速度高、低速的过渡带,其速度结构与附近区域有着明显差异,在水平和垂直方向都表现出较强的非均匀性,于是推断其存在由上地幔物质上涌随后冷却而形成的岩脉或岩体,岩浆活动引起的局部应力分布差异可能导致了地壳深部断裂的形成,造成了三河—平谷大地震的发生。Huang等(2021)也持同样观点,其发现高速区域可能与三河—平谷地震震源下方发现的局部强反射能量群相对应。由此也可看出,地壳非均匀性是影响地震发生的重要因素。大地震的发生不仅是一个简单的力学问题,与地壳的物理化学性质也密切相关。
对历史地震震级的确定方法因地震发生年代及地震记录条件的不同而不同。对有台站记录的近代地震,依然存在地震参数不准确的问题。为了修正这些地震参数,确定地震震级,有些学者提出了相关衰减方程(张方浩等,2016;Lin,Wang,2020;Fu et al,2022)、回归公式(陈培善,刘家森,1975)、地震密度计算(王健,2001)、经验地震动预测方程(Peng et al,2014)和高频GPS重建地震波(Elósegui et al,2006;Wang et al,2007;Shi et al,2010;Yin et al,2010;Bock et al,2011;Zhang et al,2012;方荣新等,2013;Hung,Rau,2013)等方法。而年代久远的历史地震只能靠当时的文字记录来推断地震强度,进而估算历史地震震级。按前人的研究方法主要从四个方面估算历史地震震级,即震中区烈度、等烈度线面积、地表破裂长度和地震影响面积。1679年三河—平谷地震震级就是依据 《乾隆三河县志》 、 《民国23年平谷县志》 等相关史料记载,利用地震烈度对照方法进行评估的(李善邦,1957)。
之后也不断有学者进行过三河—平谷地震震级相关的研究(秦四清等,2016;殷娜等,2021),发现依据现有的史料记载来评估其所处的地震区烈度,进而估算的震级,尚存有一定的争议。其次,由于存在第四系强覆盖等的影响,对于此次地震的同震破裂长度以及端部变形特征尚未有确切定义,大都估计可确认地表断裂长度在10余千米(向宏发等,1988;徐锡伟等,2000;殷娜等,2021),通过研究极震区地表断裂长度等相关参数可以看出,这显然与全球范围内震级和破裂长度之间的传统统计关系不符(Wells,Coppersmith,1994),即并不能与MW8.0震级有较好的对应,并小于震级与断层破裂长度的统计关系给出的长度,这点说明三河—平谷地震在震级与断层破裂长度统计关系的散点端,这是三河—平谷地震的一个特殊性,仅该点就足以说明该地震非常值得研究。杨百存等(2017)通过对获取的地震数据进行部分校正,认为三河—平谷地震为MW7.8。由此可见,其发震构造和机制仍需深入研究,因此本文拟在前人研究的基础上,用多震级、多破裂方式模拟三河—平谷地震的强地面运动,开展对其震级的研究,以期达到确定三河—平谷地震真实震级的目的。
1. 方法
随机有限断层法是一种很常用的地震动模拟方法,在模拟过程中可以将研究的有限断层划分为多个子断层,每个子断层可看作一个点源,考虑时间延迟后叠加每个小点源的模拟结果便可以得到整个断层的地震动模拟结果(Beresnev,Atkinson,1997)。但是传统的随机有限断层法模拟结果大多在高频段地震动可靠,基于此,Zhou和Chang (2019)提出的随机有限断层法(non-uniform stress and non-uniform window function simulation method,缩写为NNSIM)主要作了两个修改:一是将每个点源的特定时间函数替换为不同源时间函数,以提高低频结果的可靠性;二是引入非均匀的应力降,来降低模拟结果对单个应力降的依赖性,使得最终结果与实际记录更加贴合。
NNSIM随机有限断层法也沿用了传统随机有限断层法的累积思想,将大断层分为N个可视为点源的子断层,在破裂延迟和传播延迟的作用下,将每个子断层的模拟结果叠加得到整个断层的地震动效应,即
$$ a ( t ) =\sum _{i=1}^{n{\rm{l}}}\sum _{j=1}^{n{\rm{w}}}{a}_{ij} ( t+\Delta {t}_{ij} ) , $$ (1) 式中,nl和nw分别表示整个断层长度和宽度范围内分出的子断层的个数,Δtij为第ij个子断层点源到观测点的相对延时,aij(t)为在第$ ij $个子断层上用随机点源法计算得到的地震加速度,a(t)为大断层在观测点的模拟加速度。Zhou和Chang (2019)详细说明了时窗函数在低频中的作用,在此我们使用这种方法,使模拟的地震动效应中的低频部分与实际记录更加接近,从而提高全频段模拟结果的可靠性。此处的拐角频率我们使用非均匀拐角频率(Zhou,Chang,2019),则第ij个子块的角频率为
$$ {f}_{ij}=4.9 {\text{×}} {10}^{6}\beta \sqrt[{\scriptstyle3\atop {\scriptstyle\atop \scriptstyle}}]{{\frac{{\Delta {\sigma _{ij}}}}{{{M_{0ij}}}}}}, $$ (2) 式中Δσij和M0ij分别表示第ij个子断层的应力降和地震矩。Δσij由Andrews (1980)推导出的位错与应力降之间的数学关系式计算得到。
传统的随机有限断层法不断得到优化,其中一个创新就是引入了动拐角频率(Motazedian,Atkinson,2005),它是对静拐角频率乘以不同时刻破裂子断层的个数开三次方而得到,由此使得构成各子单元的震源谱的拐角频率不再相同。式(2)的物理意义明显与动拐角频率不同,但同样使得每个子断层有不同的拐角频率,且对于断层划分尺度无依赖性。关于NNSIM随机有限断层法的具体公式、变量定义等详细内容,可见之前相关研究(周红,2018;Zhou,Chang,2019;周红等,2021),作者在这三篇文章中分别用该方法对2017年九寨沟MS7.0地震、2013年芦山MS7.0地震和2021年云南漾濞MS6.4地震进行了地震动模拟,且模拟结果与实际结果重合度高,说明了此方法的有效性。现将此方法应用于1679年三河—平谷古地震的研究中。
2. 多震源的设定
通常大家都认为三河—平谷地震是一次MW8.0巨震,但是否真的如此,本文将采用多震级多破裂震源模型地震动模拟的结果对比历史烈度,达到确定真实地震震源的目标。
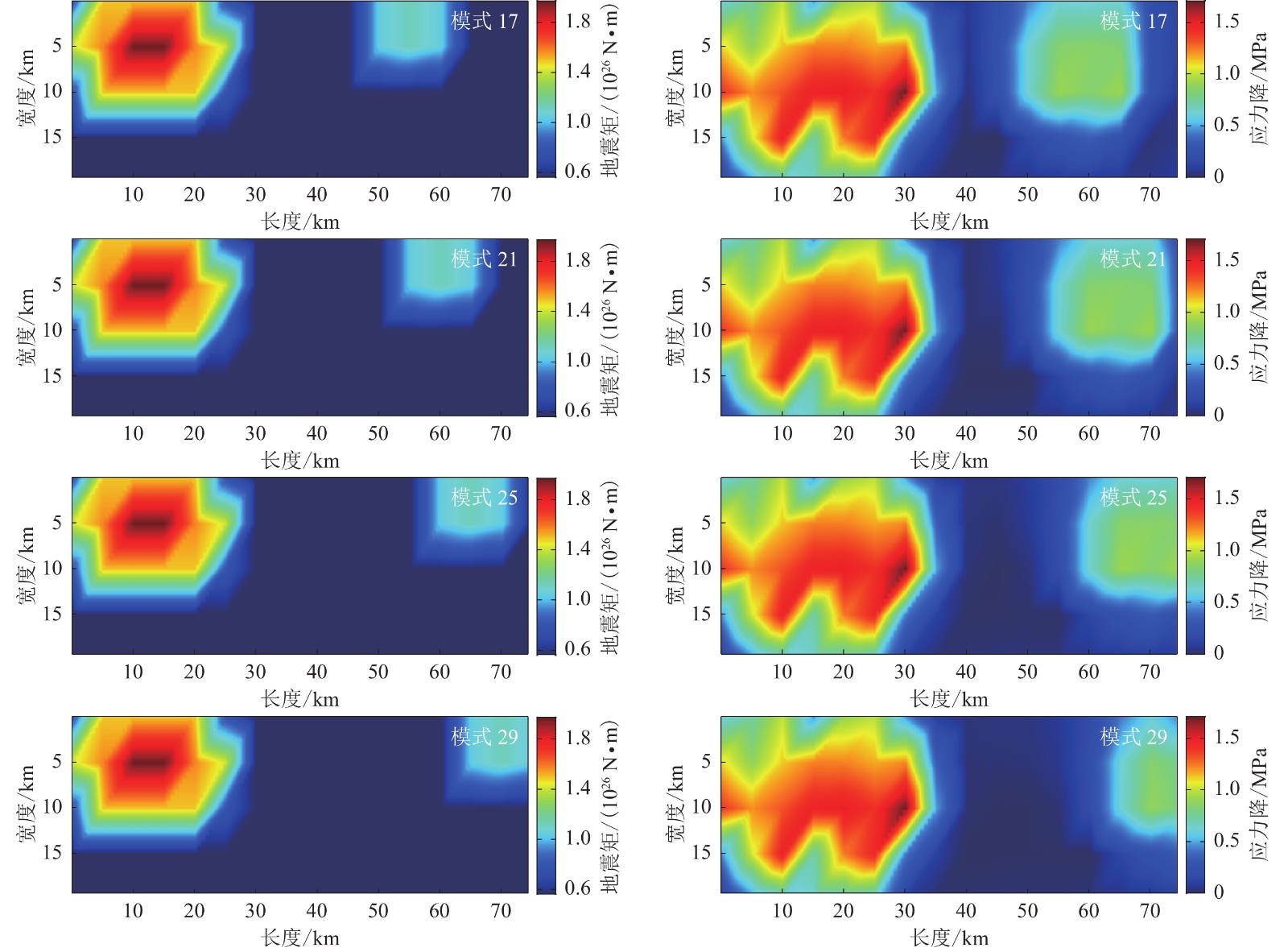
三河—平谷地震发震断层为夏垫断裂。从震级与断层长度的经验公式我们可以看出,若三河—平谷地震的震级为M8,则其断层长度应具有一个比较大的规模(董瑞树等,1993;孙银涛等,2016),但是在诸多研究中计算得到的或借鉴采用的三河—平谷地震的断层长度多数小于震级与断层长度的统计关系,也体现出三河—平谷地震的实际震级应当小于M8。Wang等(2014)结合模拟退火算法和高斯—牛顿算法,反演得出三河—平谷地震断层长度约为80 km,在其它研究中三河—平谷的研究断层长度取63—200 km不等,且在60—90 km居多(向宏发等,1988;高孟潭等,2002;潘波等,2006,2009;刘博研等,2007;付长华等,2012,2015;何付兵等,2013;朱耿尚,2014;巴振宁等,2022)。同时有研究指出,震级并不一定与断层长度完全呈正比关系,更多取决于锁固段体积、剪切弹性模量与应力降或应变增量(秦四清等,2010;杨百存等,2020;靳天伟等,2021)。于是我们在前人研究的基础上,将此次研究区域取为夏垫断裂中间部分,总长度约为80 km,宽度为25 km。震级的选择我们按0.1级增加量,将MW7.5至MW8.0分成6个震级,每个震级都按照多震源、多破裂方式进行模拟。Somerville等(1999)研究中指出M7.5以上地震进行模拟时应采用两个凹凸体,我们考虑到三河—平谷地震虽然是历史地震,但依然是华北地区著名的大地震,所以在此次研究中我们设置了两个凹凸体进行模拟。每个震级的破裂模式的确定,按照Somerville等(1999)获得的震源设定方式给定。设定方式原则如下:凹凸体个数2.6个;凹凸体面积占总破裂面积的22%;凹凸体破裂地震矩占总破裂地震矩的44%;宏观震中在主凹凸体之外;主凹凸体面积占总破裂面积的17.5%。依据如上原则,我们把夏垫断层分成80个5 km×5 km的子断层,其中沿走向为16个,沿倾向为5个。主凹凸体大小为350 km2,占14个子断层,次凹凸体大小为90 km2,占4个子断层,凹凸体位错为平均位错的两倍,剩下的62个子断层为背景位错。主凹凸体和次凹凸体在80个子断层上充分排列组合,其中主凹凸体占14个,次凹凸体占4个,且主、次凹凸体不能重合,也不能在计算区域边缘,按照这种分布形式,借助排列组合的计算方法,得到满足条件的破裂模式共180个。基于每种破裂方式的位错分布,计算出相应的应力降分布、破裂速度分布、上升时间分布及不同的震源函数,即每种位错分布可以导出复杂性地震震源。先前探槽研究显示三河—平谷地震为倾滑型地震,且走滑分量不可忽略(向宏发等,1988;张先康等,2002),所以本研究中凹凸体模型兼顾走滑与倾滑的性质,取其两个分量的平均,即45°滑动方向。图1给出了随机选择的四个震源的破裂参数分布,其中地震矩分布(图1a)可由式(3)计算得到,即
![]() 图 1 震源1,73,102和180的破裂模式所对应的强地面运动模拟结果图(c),(d)分别为为断层破裂面每个破裂子元的破裂延时和破裂初时Figure 1. Simulation results of strong ground motion corresponding to rupture modes of seismic sources 1,73,102 and 180Fig.(c) and Fig.(d) are the rupture delay and rupture initiation time for each rupture subelement of the fault rupture surface
图 1 震源1,73,102和180的破裂模式所对应的强地面运动模拟结果图(c),(d)分别为为断层破裂面每个破裂子元的破裂延时和破裂初时Figure 1. Simulation results of strong ground motion corresponding to rupture modes of seismic sources 1,73,102 and 180Fig.(c) and Fig.(d) are the rupture delay and rupture initiation time for each rupture subelement of the fault rupture surface$$ {M}_{ij}=\mu A{D}_{ij}, $$ (3) 式中,$\mu $为介质剪切模量,A为破裂面面积,$ {D}_{ij}$表示每个单元的位错。应力降分布(图1b)按Ripperger和Mai (2004)给定的式(4)计算,即
$$ \left\{\begin{array}{l}\Delta {\sigma }_{// } ( \boldsymbol{k} ) ={K}_{// } ( \boldsymbol{k} ) D ( \boldsymbol{k} ) ,\\ \Delta {\sigma }_{\perp } ( \boldsymbol{k} ) ={K}_{\perp } ( \boldsymbol{k} ) D ( \boldsymbol{k} ) ,\end{array}\right. $$ (4) 式中,${\boldsymbol{k}} $为空间波数矢量,D为波数域位错,Δσ∥和Δσ⊥分别为沿走向和倾向的应力降,K∥和K⊥分别为走向和倾向的刚度函数。图1c为断层破裂面每个破裂子元的破裂延时,它由方程Tij=1/f0ij得到。图1d为断层破裂面每个破裂子元的初始破裂时间,由tij=rij/v计算得到,这里rij为子单元到破裂起始点的距离,v为破裂速度。从四幅图中可以看出,此断层主要有两个破裂点,分别在长度约20 km处和约60 km处,其中20 km处的震源破裂更加剧烈。断层的初始破裂时间集中在0.02—0.05 s之间,最大持续时长可达22 s,产生的地震矩有7×1025 N·m,最大应力降在8 MPa附近。这四个分布是本文所使用的NNSIM模拟方法需要的震源参数。基于以上震源参数的设定开展多破裂模式下强地面运动模拟。
3. 历史烈度的对比
三河—平谷地震有详细的史料记载,可据此进行烈度评定。本文进行的历史地震烈度对比采用的是中国地震烈度标度,烈度级别共有12个,分别用罗马数字Ⅰ到Ⅻ表示。Bakun和Wentworth (1999)提出了一种直接利用烈度数据点来确定历史地震震级和震中的方法,并且得到了一些应用(Parsons et al,2000;Hinzen,Oemisch,2001;Bakun et al,2002,2003;Quadros et al,2019)。图2蓝线为近震源历史地震烈度分布曲线,棕红线为夏垫断裂带现今地震活动的地震密度,红点为三河—平谷地震的宏观震中,其位于夏垫潘各庄一带(孟宪梁等,1983)。地震活动密集分布空间展布显示夏垫断裂走向约为N50°E,从密集程度可以看出,该断裂现今地震活动仍较频繁。“地震密集值”是王健(2001)提出的参量,其全称为“震中分布分震级网格点密集值”。对于给定的震级和时间段,其能够合理地反映出地震震中的相对密集和稀疏所形成的图案,从而体现出地震的数量和震中位置的空间集中程度,在划定的研究区域内,计算出所有网格点的密集值并绘制等值线,就可以得到给定时间段内特定震级的地震活动性图像。具体计算方法在其研究(王健,2001)中有详细介绍。
为了确定三河—平谷地震的震级,首先我们把历史地震烈度曲线Ⅸ,Ⅹ,Ⅺ依据中国地震烈度表GB/T 17742−2020 (中国地震局,2020)转化成PGA和PGV峰值,即Ⅸ对应402 cm/s2,Ⅹ对应831 cm/s2,Ⅺ对应1730 cm/s2,每条曲线取约50个点。Somerville等(1999)认为最大凹凸体中心在宏观震中之外,为此我们限定最大凹凸体在宏观震中的西南。由震源设定部分的计算得出满足该限制条件的设定破裂模式共180个,利用NNSIM方法(Zhou,Chang,2019)计算比较参考场点的加速度、速度以及PGA和PGV。模拟及转化PGA和PGV的差为:
$$ \left\{\begin{array}{l}S=\displaystyle\sum _{i=1}^{150} ( \left|{\rm{PG}}{{\rm{A}}}_{{\rm{s}}i}-{\rm{PG}}{{\rm{A}}}_{{\rm{h}}i}\right|+\left|{\rm{PG}}{{\rm{V}}}_{{\rm{s}}i}-{\rm{PG}}{{\rm{V}}}_{{\rm{h}}i}\right| ) ,\\ R=\dfrac{S}{{S}_{{\rm{max}}}},\end{array}\right.$$ (5) 式中,si为模拟数据,hi为从历史事件中获得的数据。由式(5)可以看出,R和S同样反映参考场点的加速度、速度的PGA和PGV与历史烈度的差异。图3表示MW7.5到MW8.0五个震级下,每个震级的180种破裂模式对应的R值,其中R值越小,代表其模拟的PGA,PGV与历史烈度差异越小。图3显示MW7.8模拟PGA,PGV与历史烈度相差最小,其次是MW7.9,而MW8.0相差较大。其中R最小值在MW7.8的模式26。
S与R值仅表明参考场点上模拟结果与转化PGA和PGV总的差异,并不能全面反映设定地震的空间分布特征,哪个R值对应的震源激发的地震动空间分布与历史烈度一致或相近,仍需要对MW7.8,MW7.9和MW8.0模拟地震动进行空间展布并作详细对比分析。
针对MW7.8,MW7.9和MW8.0各自对应的80种破裂方式作强地面运动模拟,分别绘制Ⅸ, Ⅹ和Ⅺ烈度曲线,分析发现其中四种破裂模式(图4)产生的烈度空间分布形态与史料烈度形态接近(图5):图5a绿线为MW7.8地震四种破裂模式下的模拟烈度,其中Ⅸ, Ⅹ烈度曲线与历史烈度曲线最接近,但是MW7.8地震四种破裂模式几乎不产生Ⅺ烈度,这说明MW7.8地震在集震区不足以激发PGA大于1730 cm/s2的地震动;而MW7.9地震Ⅸ, Ⅹ烈度范围超过历史烈度圈相应范围,Ⅺ烈度圈的空间范围接近历史烈度圈的大小,但中心偏南(图5b);而MW8.0地震激发的地震烈度的范围都远大于历史烈度圈,Ⅺ, Ⅹ烈度与历史Ⅹ,Ⅸ烈度大小相似,Ⅸ烈度远大于历史Ⅸ烈度的范围(图5c),这点说明MW8.0地震产生的破裂远强于历史资料的记载。图5的对比结果显示,历史上的三河—平谷地震应该小于MW8.0,大于MW7.8,接近MW7.9,应该是一个MW7.9−或MW7.8+ +的一次强巨震。
4. 讨论与结论
本文根据多震源设定方式建立起基于地震距、应力降、断层破裂面每个破裂子元的初始破裂时间和破裂初始持时的震源破裂模型,对1679年三河—平谷大地震进行强地面运动模拟,分析其地震动破裂特征。其次,为了确定其具体震级,我们把历史地震烈度曲线依据中国地震烈度表进行转化,得到该地区烈度曲线对应的PGA和PGV峰值。利用NNSIM方法对参考场点的相关参数进行计算比较,确定MW7.8,MW7.9和MW8.0地震对应的参考场点的模拟结果与转化的PGA,PGV差异较小。基于以上结果,再用多震级多破裂方式对三个震级进行地震动模拟,并作详细对比分析,认为三河—平谷地震震级达不到MW8.0,但大于MW7.8,是一次MW7.9−或MW7.8+ +的强巨震。
本次研究有以下几个特点:
1) 多震级、多破裂方式的地震动模拟,可提供震区各场点的地震动变化范围,较一次地震的模拟结果更可信;
2) 通过对比三个震级模拟产生的地震动烈度分布,并与历史烈度对比,确定MW7.9与其一致性最高,也证明模拟中所使用的模拟方法是合适的。
研究中建立的三河—平谷地震动模拟,主要特征有以下几点:
1) 三河—平谷地震时主要有两个破裂点,并且呈现一大一小的趋势;
2) 该地震破裂面破裂持时在15—25 s内,说明破裂迅速,符合大地震的特征;
3) 主要震源破裂点在长度35 km,宽度15 km的研究区域附近,位于(117°E,40°N),此处的受灾也最为严重。
以上分析可以看出三河—平谷大地震的震级达不到MW8.0,应为MW7.9−或MW7.8+ +,这可为后续三河—平谷相关的研究提供地震动强度方面的参考。
审稿专家在本文撰写过程中提出了宝贵的意见和建议,作者在此表示感谢。
-
图 1 震源1,73,102和180的破裂模式所对应的强地面运动模拟结果
图(c),(d)分别为为断层破裂面每个破裂子元的破裂延时和破裂初时
Figure 1. Simulation results of strong ground motion corresponding to rupture modes of seismic sources 1,73,102 and 180
Fig.(c) and Fig.(d) are the rupture delay and rupture initiation time for each rupture subelement of the fault rupture surface
-
巴振宁,赵靖轩,吴孟桃,梁建文. 2022. 基于CPU-GPU异构并行的复杂场地近断层地震动谱元法模拟[J]. 地震学报,44(1):182–193. Ba Z N,Zhao J X,Wu M T,Liang J W. 2022. Simulation of near-fault ground motions in complex sites based on CPU-GPU heterogeneous parallelism by spectral element method[J]. Acta Seismologica Sinica,44(1):182–193 (in Chinese).
陈培善,刘家森. 1975. 用位错模型研究震级与烈度的关系[J]. 地球物理学报,18(3):183–195. Chen P S,Liu J S. 1975. A study of the relation between seismic magnitude and intensity by using the dislocation model[J]. Chinese Journal of Geophysics,18(3):183–195 (in Chinese).
董瑞树,冉洪流,高铮. 1993. 中国大陆地震震级和地震活动断层长度的关系讨论[J]. 地震地质,15(4):395–400. Dong R S,Ran H L,Gao Z. 1993. The relationship between earthquake magnitude and length of active fault in China[J]. Seismology and Geology,15(4):395–400 (in Chinese).
方荣新,施闯,宋伟伟,牛小骥,张全,陈克杰,刘经南. 2013. 实时GNSS地震仪系统实现及精度分析[J]. 地球物理学报,56(2):450–458. Fang R X,Shi C,Song W W,Niu X J,Zhang Q,Chen K J,Liu J N. 2013. Real-time GNSS seismometer and its accuracy[J]. Chinese Journal of Geophysics,56(2):450–458 (in Chinese).
付长华,高孟潭,陈鲲. 2012. 北京盆地结构对长周期地震动反应谱的影响[J]. 地震学报,34(3):374–382. Fu C H,Gao M T,Chen K. 2012. A study on long-period response spectrum of ground motion affected by basin structure of Beijing[J]. Acta Seismologica Sinica,34(3):374–382 (in Chinese).
付长华,高孟潭,俞言祥. 2015. 用数值模拟方法研究北京盆地对3—10 s地震动的放大效应[J]. 地震研究,38(3):448–460. doi: 10.3969/j.issn.1000-0666.2015.03.016 Fu C H,Gao M T,Yu Y X. 2015. Studying on amplification effect of Beijing basin on 3−10 s ground motion by numerical simulation method[J]. Journal of Seismological Research,38(3):448–460 (in Chinese).
高孟潭,俞言祥,张晓梅,吴健,胡平,丁彦慧. 2002. 北京地区地震动的三维有限差分模拟[J]. 中国地震,18(4):356–364. Gao M T,Yu Y X,Zhang X M,Wu J,Hu P,Ding Y H. 2002. Three-dimensional finite-difference simulations of ground motions in the Beijing area[J]. Earthquake Research in China,18(4):356–364 (in Chinese).
何付兵,白凌燕,王继明,刘予,蔡向民,孙永华,张磊,方同明,郭高轩. 2013. 夏垫断裂带深部构造特征与第四纪活动性讨论[J]. 地震地质,35(3):490–505. He F B,Bai L Y,Wang J M,Liu Y,Cai X M,Sun Y H,Zhang L,Fang T M,Guo G X. 2013. Deep structure and quaternary activities of the Xiadian fault zone[J]. Seismology and Geology,35(3):490–505 (in Chinese).
靳天伟,戚承志,陈昊祥,段秋宇,李惊涛. 2021. 锁固段对红砂岩锯齿节理面剪切特性影响因素研究[J]. 水利水电技术(中英文),52(7):175–183. Jin T W,Qi C Z,Chen H X,Duan Q Y,Li J T. 2021. Study on influencing factors of locked segment on shear characteristics of red sandstone dentate joint plane[J]. Water Resources and Hydropower Engineering,52(7):175–183 (in Chinese).
李善邦. 1957. 中国地震区域划分圖及其說明Ⅰ. 总的說明[J]. 地球物理学报,6(2):127–158. Lee S P. 1957. The map of seismicity of China[J]. Chinese Journal of Geophysics,6(2):127–158 (in Chinese).
刘保金,胡平,孟勇奇,酆少英,石金虎,姬计法. 2009. 北京地区地壳精细结构的深地震反射剖面探测研究[J]. 地球物理学报,52(9):2264–2272. Liu B J,Hu P,Meng Y Q,Feng S Y,Shi J H,Ji J F. 2009. Research on fine crustal structure using deep seismic reflection profile in Beijing region[J]. Chinese Journal of Geophysics,52(9):2264–2272 (in Chinese).
刘博研,史保平,张健. 2007. 复合地震源模拟强地面运动:以1679年三河—平谷MS8.0地震为例[J]. 地震学报,29(3):302–313. Liu B Y,Shi B P,Zhang J. 2007. Strong motion simulation by the composite source modeling:A case study of 1679 M8.0 Sanhe-Pinggu earthquake[J]. Acta Seismologica Sinica,29(3):302–313 (in Chinese).
孟宪梁,杜春涛,王瑞,刘士平. 1983. 1679年三河—平谷大震的地震断裂带[J]. 地震,(3):18–23. Meng X L,Du C T,Wang R,Liu S P. 1983. The seismic fault zone of the 1679 Sanhe-Pinggu earthquake[J]. Earthquake,(3):18–23 (in Chinese).
潘波,许建东,关口春子,何宏林. 2006. 北京地区近断层强地震动模拟[J]. 地震地质,28(4):623–634. Pan B,Xu J D,Sekigguchi H,He H L. 2006. Simulation of the near-fault strong ground motion in Beijing region[J]. Seismology and Geology,28(4):623–634 (in Chinese).
潘波,许建东,刘启方. 2009. 1679年三河—平谷8级地震近断层强地震动的有限元模拟[J]. 地震地质,31(1):69–83. Pan B,Xu J D,Liu Q F. 2009. Simulations of the near-fault strong ground motion of the 1679 Sanhe-Pinggu M8.0 earthquake[J]. Seismology and Geology,31(1):69–83 (in Chinese).
彭菲,王伟君,寇华东. 2020. 三河—平谷地区地脉动H/V谱比法探测:场地响应、浅层沉积结构及其反映的断层活动[J]. 地球物理学报,63(10):3775–3790. Peng F,Wang W J,Kou H D. 2020. Microtremer H/V spectral ratio investigation in the Sanhe-Pinggu area:Site responses,shallow sedimentary structure,and fault activity revealed[J]. Chinese Journal of Geophysics,63(10):3775–3790 (in Chinese).
彭一民,李鼎容,谢振钊,王安德,刘清泗. 1981. 北京平原区同生断裂的某些特征及其研究意义[J]. 地震地质,3(2):57–64. Peng Y M,Li D R,Xie Z Z,Wang A D,Liu Q S. 1981. Some features of contemporaneous faults in Beijing plain and their significance[J]. Seismology and Geology,3(2):57–64 (in Chinese).
秦四清,徐锡伟,胡平,王媛媛,黄鑫,泮晓华. 2010. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索[J]. 地球物理学报,53(4):1001–1014. Qin S Q,Xu X W,Hu P,Wang Y Y,Huang X,Pan X H. 2010. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction[J]. Chinese Journal of Geophysics,53(4):1001–1014 (in Chinese).
秦四清,杨百存,吴晓娲,薛雷,李培. 2016. 中国大陆某些地震区主震事件判识(Ⅱ)[J]. 地球物理学进展,31(1):115–142. Qin S Q,Yang B C,Wu X W,Xue L,Li P. 2016. The identification of mainshock events for some seismic zones in mainland China(Ⅱ)[J]. Progress in Geophysics,31(1):115–142 (in Chinese).
孙若昧,赵燕来,梅世蓉. 1993. 渤海及其邻区的地震层析成像[J]. 地球物理学报,36(1):44–54. Sun R M,Zhao Y L,Mei S R. 1993. Seismic tomographic image in Bohai Sea and its adjacent area[J]. Chinese Journal of Geophysics,36(1):44–54 (in Chinese).
孙银涛,徐国栋,龙海云,许立红. 2016. 震级与破裂长度统计关系研究[J]. 地震学报,38(5):803–806. Sun Y T,Xu G D,Long H Y,Xu L H. 2016. Relationship between magnitude and rupture length[J]. Acta Seismologica Sinica,38(5):803–806 (in Chinese).
田优平,余达远,万永革,支玲,高尔根. 2014. 三河—平谷地震区地球物理特征研究[J]. 地球物理学进展,29(4):1563–1572. Tian Y P,Yu D Y,Wan Y G,Zhi L,Gao E G. 2014. Research on the geophysical characteristics of Sanhe-Pinggu earthquake region[J]. Progress in Geophysics,29(4):1563–1572 (in Chinese).
王健. 2001. 地震活动性图象处理的网格点密集值计算方法[J]. 地震学报,23(3):262–267. Wang J. 2001. Seismic pattern treatment method through calculation of seismic density at grid nodes[J]. Acta Seismologica Sinica,23(3):262–267 (in Chinese).
向宏发,方仲景,徐杰,李如成,贾三发,郝书俭,王景钵,张晚霞. 1988. 三河—平谷8级地震区的构造背景与大震重复性研究[J]. 地震地质,10(1):15–28. Xiang H F,Fang Z J,Xu J,Li R C,Jia S F,Hao S J,Wang J B,Zhang W X. 1988. Research on the geophysical characteristics of Sanhe-Pinggu earthquake region[J]. Seismology and Geology,10(1):15–28 (in Chinese).
徐锡伟,计凤桔,于贵华,陈文彬,王峰,江娃利. 2000. 用钻孔地层剖面记录恢复古地震序列:河北夏垫断裂古地震研究[J]. 地震地质,22(1):9–19. Xu X W,Ji F J,Yu G H,Chen W B,Wang F,Jiang W L. 2000. Reconstruction of paleoearthquake sequence using stratigraphic records from drill logs:A study at the Xiadian fault,Beijing[J]. Seismology and Geology,22(1):9–19 (in Chinese).
杨百存,秦四清,薛雷,吴晓娲,张珂. 2017. 雄安新区地震危险性评估[J]. 地球物理学报,60(12):4644–4654. Yang B C,Qin S Q,Xue L,Wu X W,Zhang K. 2017. Seismic hazard assessment in the Xiong’an New Area[J]. Chinese Journal of Geophysics,60(12):4644–4654 (in Chinese).
杨百存,秦四清,薛雷,陈竑然. 2020. 锁固段损伤过程中的能量转化与分配原理[J]. 东北大学学报(自然科学版),41(7):975–981. Yang B C,Qin S Q,Xue L,Chen H R. 2020. Energy conversion and allocation principle during the damage process of locked segment[J]. Journal of Northeastern University (Natural Science),41(7):975–981 (in Chinese).
殷娜,李莹甄,纪同娟,余中元,万飞,王艳萍,贾建鹏. 2021. 1679年三河—平谷8级地震地表破裂端部特征及其地质意义[J]. 地震工程学报,43(6):1288–1293. Yin N,Li Y Z,Ji T J,Yu Z Y,Wan F,Wang Y P,Jia J P. 2021. Characteristics of the surface rupture end of the 1679 Sanhe-Pinggu M8.0 earthquake and its geological significance[J]. China Earthquake Engineering Journal,43(6):1288–1293 (in Chinese).
于湘伟,陈运泰,张怀. 2010. 京津唐地区地壳三维P波速度结构与地震活动性分析[J]. 地球物理学报,53(8):1817–1828. Yu X W,Chen Y T,Zhang H. 2010. Three-dimensional crustal P-wave velocity structure and seismicity analysis in Beijing-Tianjin-Tangshan region[J]. Chinese Journal of Geophysics,53(8):1817–1828 (in Chinese).
张方浩,蒋飞蕊,李永强,白仙富,余庆坤. 2016. 云南地区地震烈度评估模型研究[J]. 中国地震,32(3):511–521. doi: 10.3969/j.issn.1001-4683.2016.03.008 Zhang F H,Jiang F R,Li Y Q,Bai X F,Yu Q K. 2016. Study of the evaluation model of the earthquake influence in Yunnan[J]. Earthquake Research in China,32(3):511–521 (in Chinese).
张先康,赵金仁,刘国华,宋文荣,刘保金,赵成斌,成双喜,刘建达,顾梦林,孙振国. 2002. 三河—平谷8.0级大震区震源细结构的深地震反射探测研究[J]. 中国地震,18(4):326–336. Zhang X K,Zhao J R,Liu G H,Song W R,Liu B J,Zhao C B,Cheng S X,Liu J D,Gu M L,Sun Z G. 2002. Study on fine crustal structure of the Sanhe-Pinggu earthquake (M8.0) region by deep seismic reflection profiling[J]. Earthquake Research in China,18(4):326–336 (in Chinese).
周红. 2018. 基于NNSIM随机有限断层法的7.0级九寨沟地震强地面运动场重建[J]. 地球物理学报,61(5):2111–2121. Zhou H. 2018. Reconstruction of strong ground motion of Jiuzhaigou M7.0 earthquake based on NNSIM stochastic finite fault method[J]. Chinese Journal of Geophysics,61(5):2111–2121 (in Chinese).
周红,李亚南,常莹. 2021. 云南漾濞6.4级地震强地面运动的模拟和空间分布特征分析[J]. 地球物理学报,64(12):4526–4537. doi: 10.6038/cjg2021P0421 Zhou H,Li Y N,Chang Y. 2021. Simulation and analysis of spatial distribution characteristics of strong ground motions by the 2021 Yangbi,Yunnan Province MS6.4 earthquake[J]. Chinese Journal of Geophysics,64(12):4526–4537 (in Chinese).
朱耿尚. 2014. 有限差分方法在强地面运动模拟中的应用[D]. 合肥: 中国科学技术大学: 72–101. Zhu G S. 2014. Strong Ground Motion Simulation by Finite Difference Method[D]. Hefei: University of Science and Technology of China: 72–101 (in Chinese).
中国地震局. 2020. GB/T 17742−2020. 中国地震烈度表[S]. 北京: 中国国家标准化管理委员会: 9. China Earthquake Administration. 2020. GB/T 17742−2020. The Chinese Seismic Intensity Scale[S]. Beijing: Standardization Administration: 9.
Andrews D J. 1980. A stochastic fault model:1. Static case[J]. J Geophys Res:Solid Earth,85(B7):3867–3877. doi: 10.1029/JB085iB07p03867
Bakun W H,Wentworth C M. 1999. Estimating earthquake location and magnitude from seismic intensty data[J]. Bull Seismol Soc Am,89(2):557. doi: 10.1785/BSSA0890020557
Bakun W H,Haugerud R A,Hopper M G,Ludwin R S. 2002. The December 1872 Washington State earthquake[J]. Bull Seismol Soc Am,92(8):3239–3258. doi: 10.1785/0120010274
Bakun W H,Johnston A C,Hopper M G. 2003. Estimating locations and magnitudes of earthquakes in eastern North America from Modified Mercalli intensities[J]. Bull Seismol Soc Am,93(1):190–202. doi: 10.1785/0120020087
Beresnev I A,Atkinson G M. 1997. Modeling finite-fault radiation from the ω n spectrum[J]. Bull Seismol Soc Am,87(1):67–84. doi: 10.1785/BSSA0870010067
Bock Y,Melgar D,Crowell B W. 2011. Real-time strong-motion broadband displacements from collocated GPS and accelerometers[J]. Bull Seismol Soc Am,101(6):2904–2925. doi: 10.1785/0120110007
Borcherdt R D. 1991. On the observation,characterisation,and predictive GIS mapping of strong ground shaking for seismic zonation:A case study in the San Francisco Bay region,California[J]. Bull New Zealand Soc Earthquake Eng,24(4):287–305. doi: 10.5459/bnzsee.24.4.287-305
Elósegui P,Davis J L,Oberlander D,Baena R,Ekström G. 2006. Accuracy of high-rate GPS for seismology[J]. Geophys Res Lett,33(11):L11308.
Fu G, Wang Z, Liu J, Wang Y. 2022. Lithospheric equilibrium and anisotropy around the 2021 Yangbi MS6.4 earthquake in Yunnan, China[J]. Journal of Earth Science: 1–25.
Hinzen K G,Oemisch M. 2001. Location and magnitude from seismic intensity data of recent and historic earthquakes in the Northern Rhine area,Central Europe[J]. Bull Seismol Soc Am,91(1):40–56. doi: 10.1785/0120000036
Huang X Y,Yang D H,Tong P,Gao Y,Shi Y T,Wu H. 2021. Quasi-waveform seismic tomography of crustal structures in the Capital Circle region of China[J]. Science China Earth Sciences,64(1):110–126. doi: 10.1007/s11430-019-9663-4
Hung H K,Rau R J. 2013. Surface waves of the 2011 Tohoku earthquake:Observations of Taiwan's dense high-rate GPS network[J]. J Geophys Res:Solid Earth,118(1):332–345. doi: 10.1029/2012JB009689
Lin G L,Wang J. 2020. Estimation of the parameters of historical earthquakes with a new attenuation equation in Yunnan Province,China[J]. Seismol Res Lett,91(5):2651–2661. doi: 10.1785/0220200070
Motazedian D,Atkinson G M. 2005. Stochastic finite-fault modeling based on a dynamic corner frequency[J]. Bull Seismol Soc Am,95(3):995–1010. doi: 10.1785/0120030207
Parsons T,Toda S,Stein R S,Barka A,Dieterich J H. 2000. Heightened odds of large earthquakes near Istanbul:An interaction-based probability calculation[J]. Science,288(5466):661–665. doi: 10.1126/science.288.5466.661
Peng C Y,Yang J S,Xue B,Zhu X Y,Chen Y. 2014. Exploring the feasibility of earthquake early warning using records of the 2008 Wenchuan earthquake and its aftershocks[J]. Soil Dyn Earthqu Eng,57:86–93. doi: 10.1016/j.soildyn.2013.11.005
Quadros L,Assumpção M,de Souza A P T. 2019. Seismic intensity attenuation for intraplate earthquakes in Brazil with the re-evaluation of historical seismicity[J]. Seismol Res Lett,90(6):2217–2226. doi: 10.1785/0220190120
Ripperger J,Mai P M. 2004. Fast computation of static stress changes on 2D faults from final slip distributions[J]. Geophys Res Lett,31(18):L18610. doi: 10.1029/2004GL020594
Shi C,Lou Y,Zhang H,Zhao Q,Geng J,Wang R,Fang R,Liu J. 2010. Seismic deformation of the MW8.0 Wenchuan earthquake from high-rate GPS observations[J]. Adv Space Res,46(2):228–235. doi: 10.1016/j.asr.2010.03.006
Somerville P,Irikura K,Graves R,Sawada S,Wald D,Abrahamson N,Iwasaki Y,Kagawa T,Smith N,Kowada A. 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J]. Seismol Res Lett,70(1):59–80. doi: 10.1785/gssrl.70.1.59
Wang G Q,Boore D M,Tang G Q,Zhou X Y. 2007. Comparisons of ground motions from colocated and closely spaced one-sample-per-second global positioning system and accelerograph recordings of the 2003 M6.5 San Simeon,California,earthquake in the Parkfield region[J]. Bull Seismol Soc Am,97(1B):76–90. doi: 10.1785/0120060053
Wang X S,Feng X D,Xu X W,Diao G L,Wan Y G,Wang L B,Ma G Q. 2014. Fault plane parameters of Sanhe-Pinggu M8.0 earthquake in 1679 determined using present-day small earthquakes[J]. Earthquake Science,27(6):607–614. doi: 10.1007/s11589-014-0099-3
Wells D L,Coppersmith K J. 1994. New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J]. Bull Seismol Soc Am,84(4):974–1002.
Yin H T,Zhang P Z,Gan W J,Wang M,Liao H,Li X J,Li J,Xiao G R. 2010. Near-field surface movement during the Wenchuan MS8.0 earthquake measured by high-rate GPS[J]. Chinese Science Bulletin,55(23):2529–2534. doi: 10.1007/s11434-010-4026-2
Zhang X H,Guo F,Guo B F,Lü C X. 2012. Coseismic displacement monitoring and wave picking with high-frequency GPS[J]. Chinese Journal of Geophysics,55(6):1912–1918.
Zhou H,Chang Y. 2019. Stochastic finite-fault method controlled by the fault rupture process and its application to the MS7.0 Lushan earthquake[J]. Soil Dyn Earthq Eng,126:105782. doi: 10.1016/j.soildyn.2019.105782
-
期刊类型引用(1)
1. 刘长生,刘学谦,周晨,李娇,高峰. 绥化地震台视电阻率数据跟踪分析. 地震地磁观测与研究. 2024(06): 72-82 .  百度学术
百度学术
其他类型引用(0)





 下载:
下载: