Vulnerability analyses of masonry structure under induced earthquake
-
摘要:
为揭示诱发地震和天然地震对建筑结构影响及其破坏概率分布的影响，本文以我国典型砌体结构为研究对象，开展了考虑诱发地震影响的易损性研究。首先建立了典型三层和六层砌体结构分析模型，然后以40条震级和震中距都接近的天然地震地震动和诱发地震地震动为输入开展Pushover分析，分别建立基于峰值加速度PGA和结构基本周期加速度反应谱值Sa的易损性曲线，最后采用循环往复加载方法对两次诱发地震作用下的结构倒塌易损性进行了分析讨论。结果表明：当以PGA作为易损性输入地震动参数时，天然地震地震动作用下的易损性显著高于诱发地震地震动；当以Sa作为易损性输入地震动参数时，三层砌体结构由于以基本振型为主导，在两类地震动作用下其易损性曲线比较接近，而六层砌体结构高阶振型由于对结构地震响应具有一定影响，且诱发地震地震动的高频成分较天然地震地震动丰富，因此六层砌体结构在诱发地震地震动作用下的易损性高于天然地震。此外，对两次诱发地震作用下的砌体结构易损性分析结果表明两次地震作用下结构的损伤概率明显增加。
-
关键词:
- 诱发地震 /
- 天然地震 /
- 砌体结构 /
- Pushover分析 /
- 地震易损性分析
Abstract:The impact of earthquake induced by shale gas mining has attracted the attention of the government, academia and the public. It is of scientific significance and application value for the prevention and control of earthquake disaster risk to carry out seismic vulnerability research of induced earthquakes. There are significant differences between induced earthquakes and natural earthquakes in ground motion characteristics, and their seismic responses to engineering structures are also very different. In order to reveal the influence of induced earthquake and natural earthquake on the seismic effects of building structure and the distribution of failure probability of masonry structure, this paper takes typical masonry structure as the research object and develops the vulnerability study considering the effects of induced earthquake. At first, analysis models of typical three-story and six-story masonry structures are established, and then 40 natural ground motions and induced seismic ground motion with similar magnitude and epicenter distances are selected as inputs to the Pushover analysis. Finally vulnerability curves based on peak ground acceleration （PGA） and basic periodic acceleration response spectrum value Sa of the structure are established respectively. The cyclic loading method is used to analyze and discuss the structural collapse vulnerability under two induced earthquakes. The analysis shows that the induced seismic ground motion contains more high frequency components, while the natural ground motion has more low frequency components, when PGA is used as the vulnerability parameter, the vulnerability of natural ground motion is significantly higher than that of induced seismic ground motion. When Sa is used as the vulnerability parameter to input ground motion, the vulnerability curves of the three-story masonry structure are close to each other under the action of two kinds of ground motions because the basic mode is dominant. However, the high-order mode of six-story masonry structure has some influence on the seismic response of the structure, and the high-frequency components of induced seismic ground motion are more abundant than those of natural ground motion, so the vulnerability of six-story masonry structure under induced seismic ground motion is higher than that of natural ground motion. In addition, the cyclic loading method is used to analyze the vulnerability of masonry structures under the two induced earthquakes. The results show that the damage probability of structures increases obviously under the action of two induced earthquakes.
-
引言
随着页岩气大量开采，诱发地震数量急剧增加，引起了全球的广泛关注。美国俄克拉荷马州（Oklahoma）页岩气田和荷兰格罗宁根（Groningen）天然气田规模化开采后，地震频次明显增加，开采区的房屋遭受严重的损坏（Walsh，Zoback，2015；Mulder，Perey，2018）；我国2014年后对四川长宁、威远和重庆涪陵焦石坝等区域进行了规模化页岩气开采，原本地震活动性较低的地区地震频次大幅上升，造成了重大经济损失和严重后果（何登发等，2019；Yang et al，2020）。为了对诱发地震灾害进行有效防控，须定量地分析诱发地震对我国一般房屋建筑的影响。
房屋建筑地震易损性分析是开展地震灾害风险评估的关键环节。国外对于房屋结构的诱发地震影响已有一些研究，例如：Crowley等（2017，2019）建立了荷兰格罗宁根区域的建筑群模型，给出了当地不同砖砌体结构与非结构构件的倒塌和损伤易损性函数，并对诱发地震导致人员伤亡风险进行了评估；Kurkowski （2018）研究了诱发地震作用下砌体饰面的易损性；Chase等（2019）采用Pushover分析方法，建立了美国俄克拉荷马州轻型木框架建筑考虑诱发地震影响的易损性函数，并研究了诱发地震作用下的结构累积损伤效应；Kallioras等（2019）对不同结构进行了振动台试验，研究了无筋砌体结构的动力性能，建立了诱发地震作用下的无筋砌体结构易损性模型；Silva等（2021）基于Pushover分析方法建立了巴西典型结构和非结构构件考虑诱发地震影响的易损性函数。
鉴于我国页岩气开采时间较晚，有关考虑诱发地震影响的建筑结构易损性分析目前尚未见相关报道，还缺少考虑诱发地震地震动作用的结构易损性模型。尽管国外学者已对砌体及木框架结构的诱发地震易损性展开了研究，但仍然没有关于天然地震和诱发地震作用下的易损性模型对比研究，未能揭示天然地震地震动与诱发地震地震动影响的差异。此外，在开展考虑诱发地震地震动作用的结构易损性分析时，如未考虑多次诱发地震地震动作用引起的累积损伤效应，可能会低估多次诱发地震地震动作用下的结构破坏概率。鉴于此，本文以天然地震地震动及诱发地震地震动作为输入，对比研究两类地震动对砌体结构影响的差异，并采用循环往复分析方法研究多次诱发地震地震动作用下的累计损伤效应，以分析诱发地震对我国一般房屋建筑的影响。
1. 基于Pushover能力谱法的地震易损性分析方法
1.1 地震易损性概率模型
结构的地震易损性是指在给定强度水平的地震动作用下结构超越一定破坏状态的条件概率，即：
$$ {P_{\text{f}}} ＝ P ［ D {\text{≥}} C\,|\, IM{{ ＝ }}x] ］ \text{，} $$ (1) 式中：Pf为地震动强度为x时结构超越某破坏状态的条件概率；D为结构需求参数；C为结构能力参数；IM为地震动强度指标。
一般认为，对数正态分布是比较理想的易损性概率模型，即结构需求参数D和结构能力参数C均服从对数正态分布，则易损性可以表示为
$$ {P_{\text{f}}} ＝ \varPhi \left(\frac{{\ln {DM_{IM ＝ x}} － \ln {\mu _C}}}{{\sqrt {{\beta _C^2} ＋ {\beta _D^2}} }}\right) \text{，} $$ (2) 式中：Φ（x）为标准正态分布函数；DMIM＝x为地震动强度为x时的结构需求中值；μC为对应于不同破坏状态的结构能力参数中值；βD和βC分别为结构需求参数和破坏状态对应结构能力参数的对数标准差。
1.2 易损性分析方法
根据易损性概率模型，易损性分析的关键是确定在给定强度水平地震动作用下结构需求参数的统计特征，以及破坏状态对应的结构能力参数的统计特征。一方面，可以基于结构地震响应分析建立结构地震需求与地震动强度指标之间的统计关系，即结构概率地震需求模型；另一方面，可基于理论分析及试验数据确定结构不同破坏状态对应的结构能力参数统计特征，即破坏准则。
本文采用Pushover能力谱法建立结构的概率地震需求模型。Pushover分析是对结构进行静力单调加载下的弹塑性分析方法。该方法将地震荷载等效成水平分布的侧向力施加在结构上，并逐渐增大水平力或水平位移，直至结构的控制点达到目标位移或结构倾覆。Pushover分析方法模型简单，且分析结果与时程分析结果相近，是可行的弹塑性分析方法（张勇，2013；Murat et al，2019）。对于总高度较低且弹塑性地震响应主要取决于第一振型的结构，Pushover分析方法所得结果的误差较小（缪志伟等，2008）。
基于Pushover分析得到大量结构需求参数及其对应的地震动参数后，可通过下式确定结构需求参数中值DM与地震动强度参数IM之间的关系，以及结构需求参数的对数标准差βD （Shome，1999；Cornell et al，2002）：
$$ \ln D{M_{IM ＝ x}} ＝ a ＋ {{b}}\ln x \text{，} $$ (3) 式中a和b为回归系数，根据结构地震响应与地震动参数之间的对数线性回归确定，对数线性回归的标准差即为βD。
砌体结构破坏等级通常可分为 “基本完好” 、 “轻微破坏” 、 “中等破坏” 、 “严重破坏” 、 “毁坏”等五类。由于砌体结构自重大，抗剪切能力差，一般将延性系数作为指标来表示砌体结构在地震动作用下的需求参数，本文中的延性系数是指砌体结构在地震动作用下极限位移与屈服位移之比。参考郝敏等（2007）对砌体结构延性系数与破坏等级关系的研究，采用延性系数作为变形指标进行划分，延性系数与破坏等级的关系如表1所示。根据延性系数与破坏等级的关系可确定各破坏状态所对应结构能力参数限值（表1中第三列），本文不考虑结构能力参数的不确定性，即βC＝0。
表 1 砌体结构延性系数与破坏等级之间的关系（郝敏等，2007）Table 1. Relationship between ductility coefficient and damage grade of masonry structure （Hao et al，2007）破坏等级 延性系数μ 能力参数限值 基本完好 μ≤0.68 轻微破坏 0.68＜μ≤1.3 0.68 中等破坏 1.3＜μ≤3.5 1.3 严重破坏 3.5＜μ≤6.5 3.5 毁坏 μ＞6.5 6.5 最后，给定强度水平x的地震动作用下的结构易损性可采用下式计算：
$$ {P_{\text{f}}} ＝ \varPhi \left(\frac{{a ＋ {{b}}\ln x － \ln {\mu _{\rm{C}}}}}{{{\beta _{\rm{D}}}}}\right) {\text{.}} $$ (4) 2. 砌体结构分析模型及地震动选择
2.1 砌体结构模型
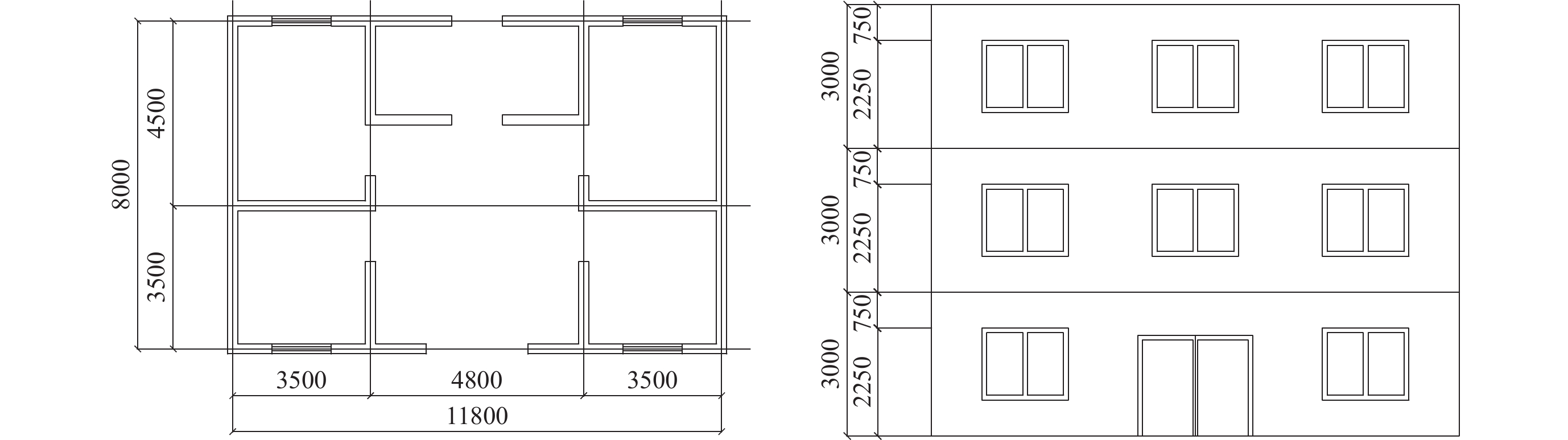
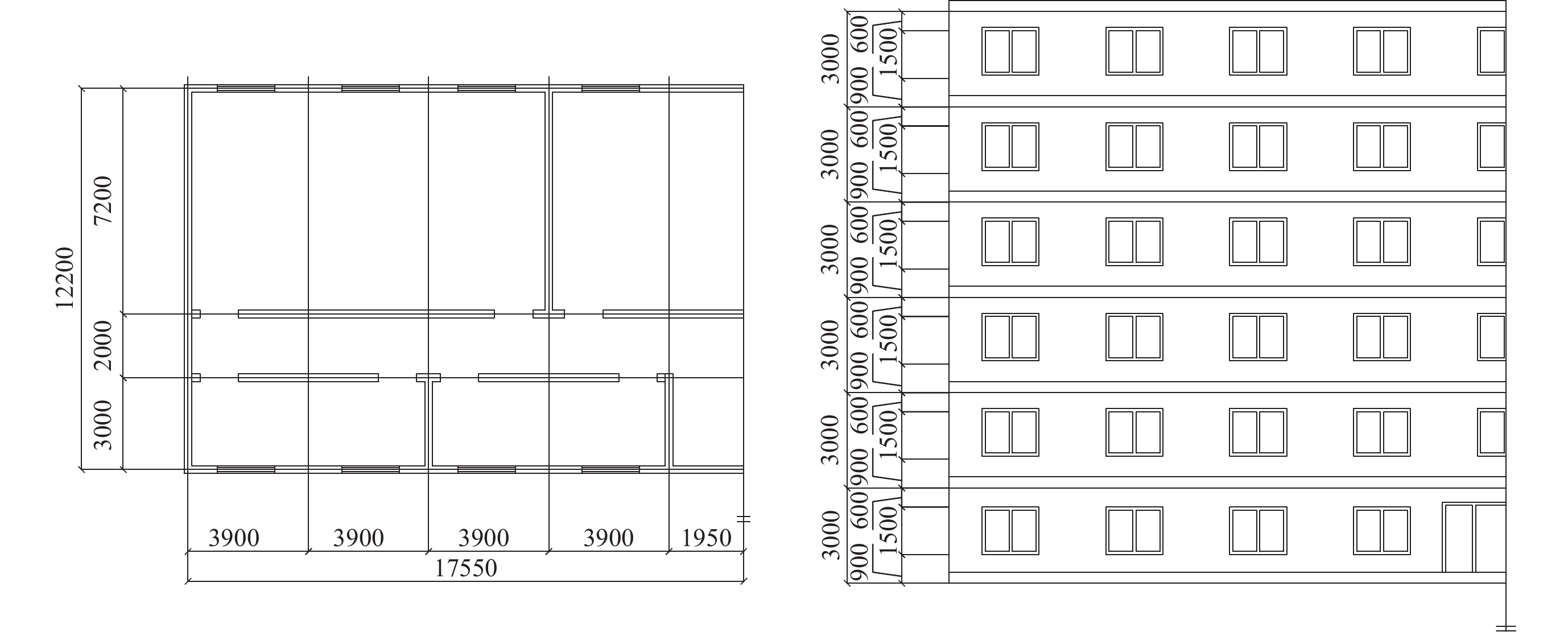
选取我国西南页岩气开采地区典型的三层、六层砌体结构为研究对象，承重墙采用烧结黏土砖，等级为MU15，砂浆强度等级为M5。三层结构长11.8 m，宽7 m；六层结构长35.1 m，宽12.2 m。两种结构层高均为3 m，纵横墙承重，墙厚均为240 mm。楼面和屋面均采用120 mm厚钢筋混凝土楼板，选用C20混凝土。楼面活荷载为3 500 N/m2，屋面活荷载为4 500 N/m2，三层、六层结构的基本周期为0.15 s和0.34 s，相应的结构布置图分别见图1和图2。
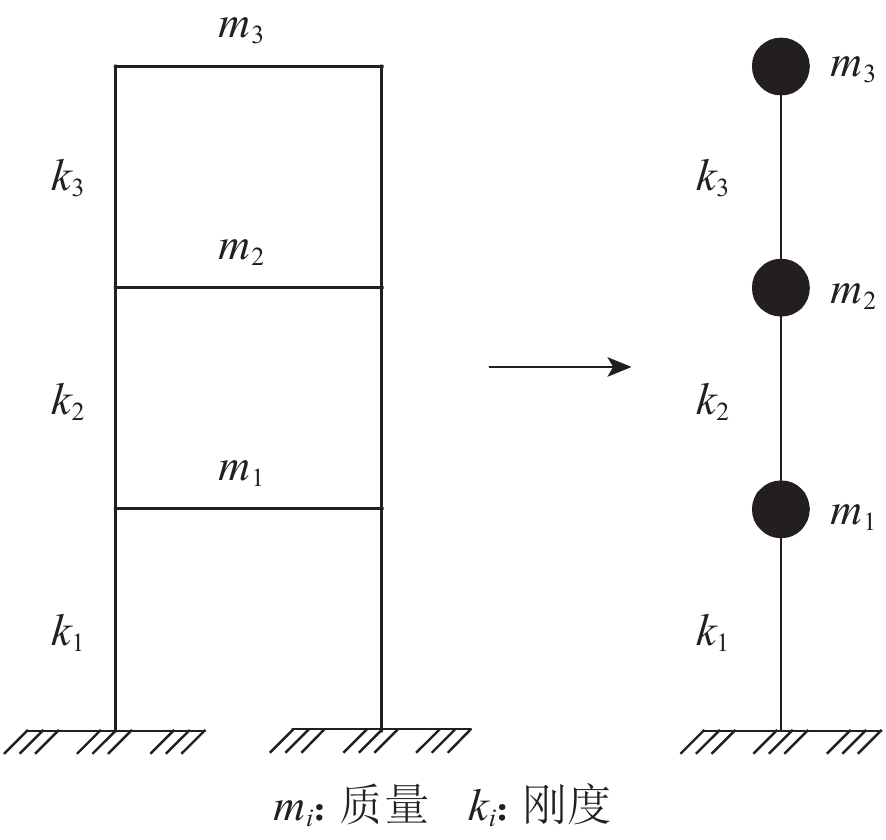
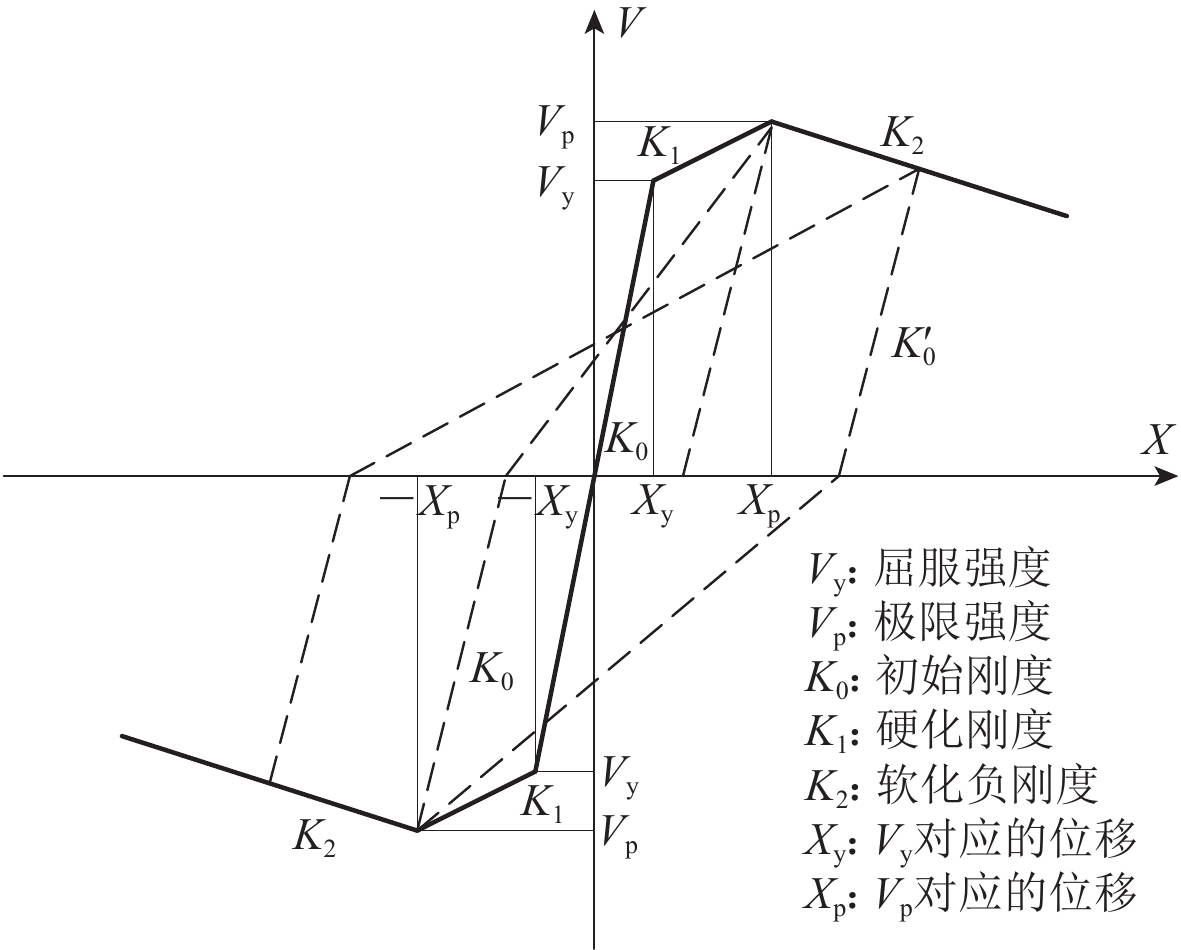
砌体结构高和宽较小，地震中以剪切破坏为主，一般使用层间剪切模型（图3）对结构进行非线性地震反应分析，其中ki为第i层刚度，mi为第i层质量。假定建筑物各层楼板平面内刚度无限大，水平地震动作用下各楼层竖向构件的侧向位移相同。国内外学者对砌体恢复力模型进行了大量研究，得到了基于数学表达式的理想化结构恢复力曲线，本文选用张令心等（2002）总结大量有无构造柱的砖墙体试验数据得到的考虑构造柱影响的恢复力模型，如图4所示。该模型为三线性刚度退化模型，不仅考虑了墙体正反向加载时软化段的特性，还结合了卸载段刚度退化的规则，该模型有五个独立参数，即屈服强度（Vy）、极限强度（Vp）、初始刚度（K0）、硬化刚度（K1）和软化负刚度（K2）。选用张令心等（2002）提出的砌体墙段抗侧移刚度计算方法对砌体墙段及构造柱刚度进行计算，计算方法如下所述，结构层间刚度为砌体各墙段的刚度值之和。
![]()
图 3 砌体结构层间剪切模型示意图Figure 3. Schematic diagram of interlayer shearing model of masonry structure![]()
图 4 三线性恢复力模型示意图（张令心等，2002）Figure 4. Schematic diagram of trilinear restoring of masonry structure force model （after Zhang et al，2002）2.1.1 砌体墙段刚度
1） 初始刚度K0。
① 对于无孔洞、无构造柱墙段，
$$ \begin{split} \\ {K_0} ＝ \left\{ \begin{array}{l} \dfrac{{G{A_{\rm{t}}}}}{{\xi h}} \qquad \quad \qquad \,\,\,\,\,\,\,\, h/b＜1 \text{，} \\ \dfrac{{G{A_{\rm{t}}}}}{{1.2h\left(1 ＋ \dfrac{{{h^2}}}{{3{b^2}}}\right)}} \qquad 1 {\text{≤}} h/b {\text{≤}} 4 \text{，} \end{array} \right. \end{split} $$ (5) 式中：At为墙段水平截面总面积；h为砌体墙段层间计算高度；b为墙段水平截面宽度；G为砌体剪切模量，是砌体弹性模量的2/5；ξ为砌体剪应力不均匀影响系数，矩形截面取1.2。当h/b＞4时不考虑其刚度。
② 对于设有构造柱或有开洞的墙段，
$$ {K_0} ＝ {\lambda _0}\frac{{G{A_{\rm{t}}}}}{{\xi h}} \text{，} $$ (6) 式中，$ {\lambda }_{0} $为砌体墙段考虑弯曲和开洞影响的刚度修正系数，计算公式如下：
$$ {\lambda _0} ＝ \left\{ \begin{array}{l} \dfrac{{{\varphi _0}{A_{\text{z}}}}}{{{A_{\rm{t}}}}}\qquad \quad \qquad \,\,\,\,\,\,\,\, h/b＜1 \text{，} \\ \dfrac{{{\varphi _0}}}{{1 ＋ \dfrac{{G{A_{\text{z}}}}}{\xi } \dfrac{{{h^2}}}{{12E{\boldsymbol{I}}}}}} \qquad 1 {\text{≤}} h/b {\text{≤}} 4 \text{，} \end{array} \right. $$ (7) 式中：φ0为砌体墙段开洞影响系数，按照墙体开洞率A/At来取值，具体取值列于表2，其中A为不考虑洞口的墙体水平截面积；Az为砌体墙段水平截面折算面积，计算公式为
表 2 砌体墙段开洞影响系数Table 2. Influence coefficient of masonry wall with opening开洞率 影响系数φ0 开洞率 影响系数φ0 0.9 0.98 0.6 0.76 0.8 0.94 0.5 0.68 0.7 0.88 0.4 0.56 $$ {A_{\text{z}}} ＝ {A_{{\rm{j}}{\text{z}}}} ＋ {\eta _{\rm{g}}}\frac{{{E_{\rm{c}}}}}{E}{A_{\rm{c}}}\text{，} $$ (8) 式中：Ac为墙段扣除开洞及构造柱的水平截面积；Ec为混凝土构造柱弹性模量；Ajz为墙体扣除开洞与构造柱水平截面积之后的墙体水平净截面积；ηg为考虑构造柱钢筋参与墙体工作的工作系数，当h/b≥0.5时，ηg＝0.30，当h/b＜0.5时，ηg＝0.26；I为墙体构造柱水平截面积之和按其混凝土弹性模量与砖砌体弹性模量的比值折算后，与墙体水平净截面积一起按照“I”字型截面计算的惯性矩。
2） 硬化刚度K1和软化负刚度K2。计算公式为：
$$ {K_1} ＝ {\alpha _1}{K_0}\text{，} \,\,\, {K_2} ＝ {\alpha _2}{K_0}\text{，} $$ (9) 式中，α1为硬化比，α2为软化系数。当不考虑构造柱作用时，α1＝0.18，α2＝−0.166；当考虑构造柱作用时，α1＝0.075，α2＝−0.056。
3） 卸载刚度Ku。计算公式为：
$$ {K_{\rm{u}}} ＝ {\left(\frac{X}{{{X_{\rm{c}}}}}\right)^{{\alpha _3}}}{K_0} $$ (10) 式中：X为墙体卸载时的层间位移，Xc为墙体开裂时的层间位移；α3为卸载系数，当不考虑构造柱作用时，α3＝−0.60；当考虑构造柱作用时，α3＝−0.53。
2.1.2 砌体墙段强度截面强度
屈服强度Vy的计算公式为：
$$ {V_{\rm{y}}} ＝\left\{ \begin{array}{l} \dfrac{{A{\tau _{{\rm{k}}， x}}}}{\xi }\sqrt {1 ＋ \dfrac{{{\sigma _0}}}{{{\tau _{{\rm{k}}， x}}}}} \qquad \,\,\, 不考虑构造柱\text{，} \\ \dfrac{{{A_{\text{z}}}{\tau _{{\rm{k}}， x}}}}{\xi }\sqrt {1 ＋ \dfrac{{{\sigma _0}}}{{{\tau _{{\rm{k}}， x}}}}} \qquad 考虑构造柱 \text{，} \end{array} \right.$$ (11) 极限强度Vp的计算公式为：
$${V_{\rm{p}}} ＝ {\alpha _{\rm{y}}}{V_{\rm{y}}}\text{，} \quad \,\,\,\,\, \, 不考虑构造柱时\,{\alpha _{\rm{y}}} = 1.192 \text{，} 考虑构造柱时\, {\alpha _{\rm{y}}} = 1.110 \text{，} $$ (12) 式中：τk， x为砌体沿灰缝的抗剪强度，σ0为首层墙段中间高度平均压应力，A为墙段净截面面积。
2.2 地震动的选取
为减少诱发地震地震动的不确定性对分析结果的影响，从Assatourians和Atkinson （2019）开发的诱发地震数据库中随机选取40条原始水平地震动加速度记录，震级的分布范围为4.1—5.7，震中距的分布范围为2.00—31.40 km，场地类型均为Ⅱ类；此外，从美国太平洋地震工程研究中心（Pacific Earthquake Engineering Research Center，缩写为PEER）强震数据库中选取震中距及震级相近、场地类型相同的40条原始水平地震动加速度记录。所选取的地震动记录基本信息列于表3。
表 3 天然地震地震动与诱发地震地震动记录的基本信息Table 3. Basic information of ground motion records of natural and induced earthquakes诱发地震 天然地震 诱发地震 天然地震 M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
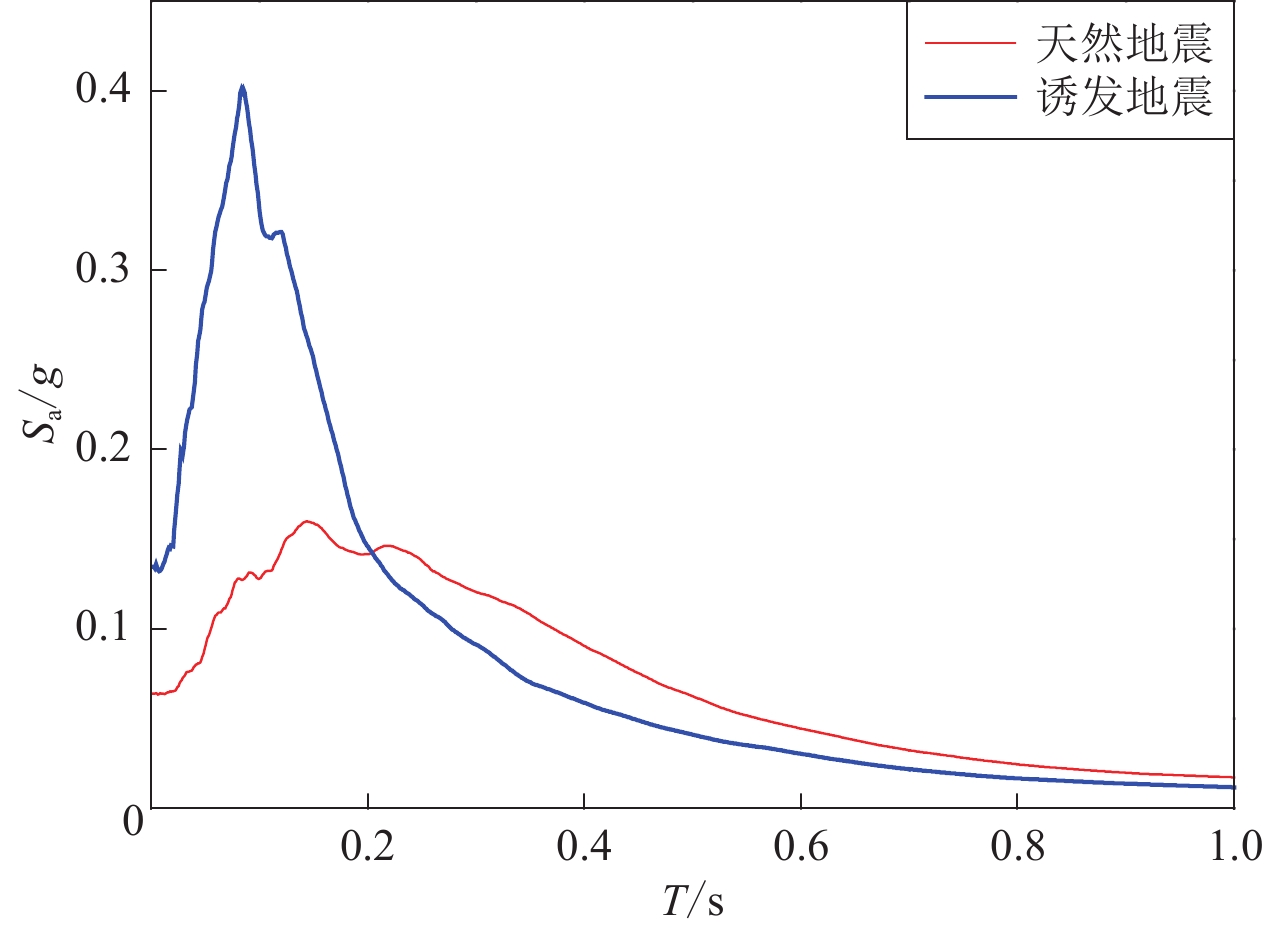
/（cm·s−2）4.7 12.95 14.04 4.79 13.55 38.97 4.9 31.4 27.71 4.92 31.71 30.24 4.7 2.71 63.94 4.7 2.84 158.0 4.9 15.02 69.84 4.92 14.94 38.79 5.7 27.29 62.39 5.7 27.78 36.42 4.3 3.95 197.5 4.27 3.69 20.02 4.8 27.63 63.60 4.88 27.89 103.6 4.4 6.02 231.6 4.45 6.46 33.72 4.5 5.17 36.20 4.6 5.2 184.5 4.5 7.28 43.7 4.45 7.46 63.36 4.5 10.04 19.55 4.6 10.16 12.10 4.1 2.0 261.5 4.12 1.42 167.51 4.5 4.47 367.8 4.45 4.7 29.43 4.1 4.23 97.21 4.1 4.41 99.87 4.3 2.47 215.5 4.27 2.67 48.83 4.4 6.71 114.9 4.37 6.48 6.004 4.3 5.66 267.6 4.3 5.28 37.54 4.4 4.9 162.1 4.45 4.7 29.44 4.1 2.76 284.6 4.05 2.93 21.93 4.4 1.7 341.5 4.45 1.0 159.68 4.1 5.42 380.0 4.1 5.39 84.58 4.4 4.53 116.1 4.5 4.62 57.93 4.4 2.88 152.7 4.45 2.38 216.77 4.7 27.22 49.30 4.77 26.39 8.036 4.3 8.57 154.4 4.2 8.32 54.57 4.4 6.9 38.51 4.5 6.35 26.75 4.3 8.55 144.4 4.3 8.76 68.84 4.7 23.32 30.87 4.7 23.47 15.42 4.3 2.48 666.5 4.3 2.67 48.83 4.7 16.2 51.80 4.7 16.05 16.94 4.3 6.96 51.38 4.26 7.34 14.54 4.3 3.39 255.1 4.26 3.45 44.97 4.9 17.91 72.05 4.9 18.46 26.19 4.2 3.68 284.8 4.2 3.34 71.14 4.9 24.25 47.49 4.92 24.5 36.80 4.2 7.92 33.5 4.2 7.98 120.56 4.9 28.69 37.40 4.92 29 59.15 4.2 5.52 19.80 4.3 5.14 24.57 4.9 21.21 37.72 4.9 21.48 28.98 4.2 5.84 413.7 4.2 5.31 245.06 所选取的诱发地震与天然地震的地震动加速度反应谱及其平均谱如图5所示。将诱发地震与天然地震记录的平均加速度反应谱进行对比，结果如图6所示。由图5和图6可以看出：在震级和震中距都接近的条件下，诱发地震加速度反应谱Sa值在5 Hz以上的高频段大于天然地震，且平均加速度反应谱峰值远大于天然地震；诱发地震平均加速度反应谱在达到峰值后迅速衰减，在5 Hz以下频段小于天然地震平均加速度反应谱值。可见，诱发地震的地震动以高频成分为主，低频成分较少，主要影响基本自振周期为0.1 s左右的低矮建筑。
![]()
图 5 诱发地震（a）和天然地震（b）的地震动加速度反应谱Figure 5. Ground motion acceleration response spectra of induced earthquake （a） and natural earthquake （b）![]()
图 6 诱发地震与天然地震的平均地震动加速度反应谱Figure 6. Mean ground motion acceleration response spectra of induced and natural earthquakes3. 结构地震易损性分析
3.1 结构概率地震需求模型
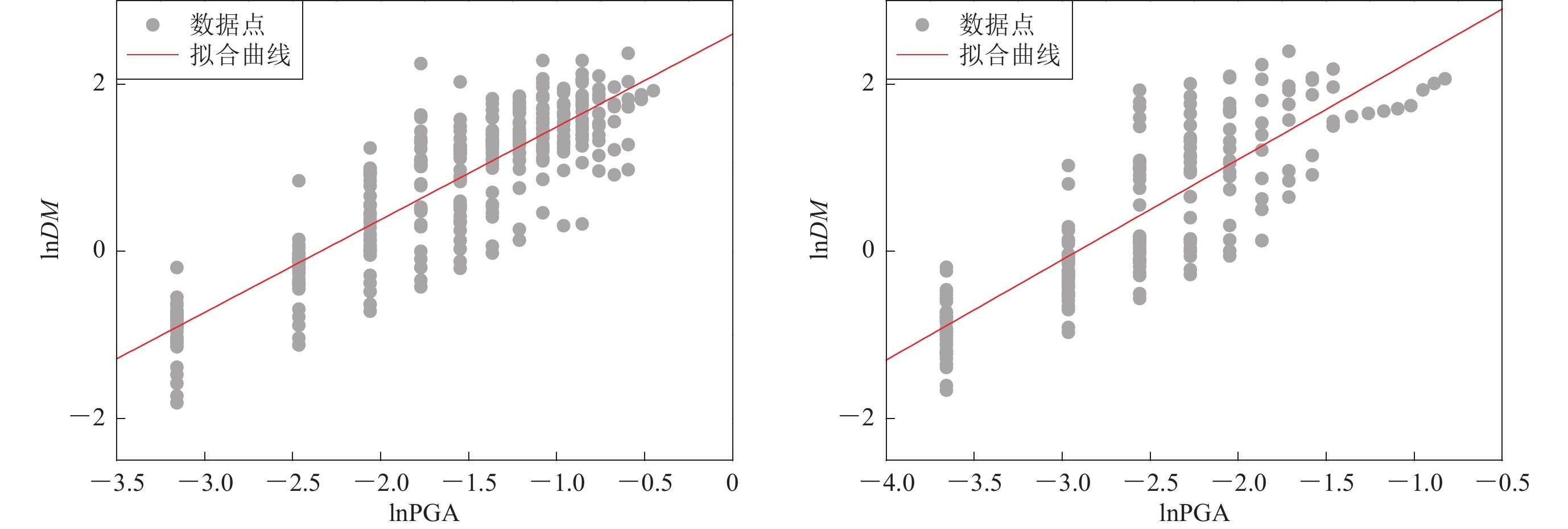
分别对选取的40条诱发地震加速度记录进行PGA归一化处理后等间距调幅，增幅步长为0.05g，之后对砌体结构模型进行Pushover分析，荷载分布采用倒三角形分布侧向加载。考虑到峰值加速度指标对于短周期结构的相关性更高（叶列平等，2009），加速度反应谱是单自由度结构体系在地震动作用下的最大响应，同时反映了地震动和建筑结构的自身特性，因此本文以峰值加速度PGA和结构一阶周期对应的加速度反应谱值Sa作为地震动强度参数，计算在给定地震动强度参数下结构的延性系数。将结构延性系数DM分别与峰值加速度PGA和结构一阶周期对应的加速度反应谱值Sa进行对数线性回归拟合，得到结构概率地震需求模型。三层砌体结构概率地震需求模型如图7a所示。再按相同方法对天然地震地震动进行处理，进行Pushover分析，计算结构延性系数，与PGA和Sa进行对数线性回归拟合，得到天然地震下结构概率地震需求模型，如图7b所示。详细拟合参数列于表4。
![]()
图 7 诱发地震（a）与天然地震（b）的三层结构地震概率需求模型Figure 7. Probabilistic seismic demand models of three-story structure for induced earthquakes （a） and natural earthquakes （b）表 4 不同地震及结构类型关于PGA和Sa的拟合参数Table 4. Fitting parameters of different seismic and structural types结构类型 地震类型 地震动参数 拟合结果 拟合优度 均方根误差 三层砌体 诱发地震 PGA lnDM＝1.11 lnPGA＋2.60 0.78 0.62 天然地震 PGA lnDM＝1.20 lnPGA＋2.90 0.71 0.56 诱发地震 Sa lnDM＝1.05 lnSa＋1.46 0.84 0.36 天然地震 Sa lnDM＝1.17 lnSa＋1.54 0.77 0.50 六层砌体 诱发地震 PGA lnDM＝1.04 lnPGA＋1.50 0.73 0.55 天然地震 PGA lnDM＝1.20lnPGA＋2.28 0.81 0.51 诱发地震 Sa lnDM＝0.97lnSa＋1.64 0.63 0.71 天然地震 Sa lnDM＝1.16lnSa＋1.61 0.64 0.69 注：DM为结构延性系数。 3.2 单次地震下结构的地震易损性分析
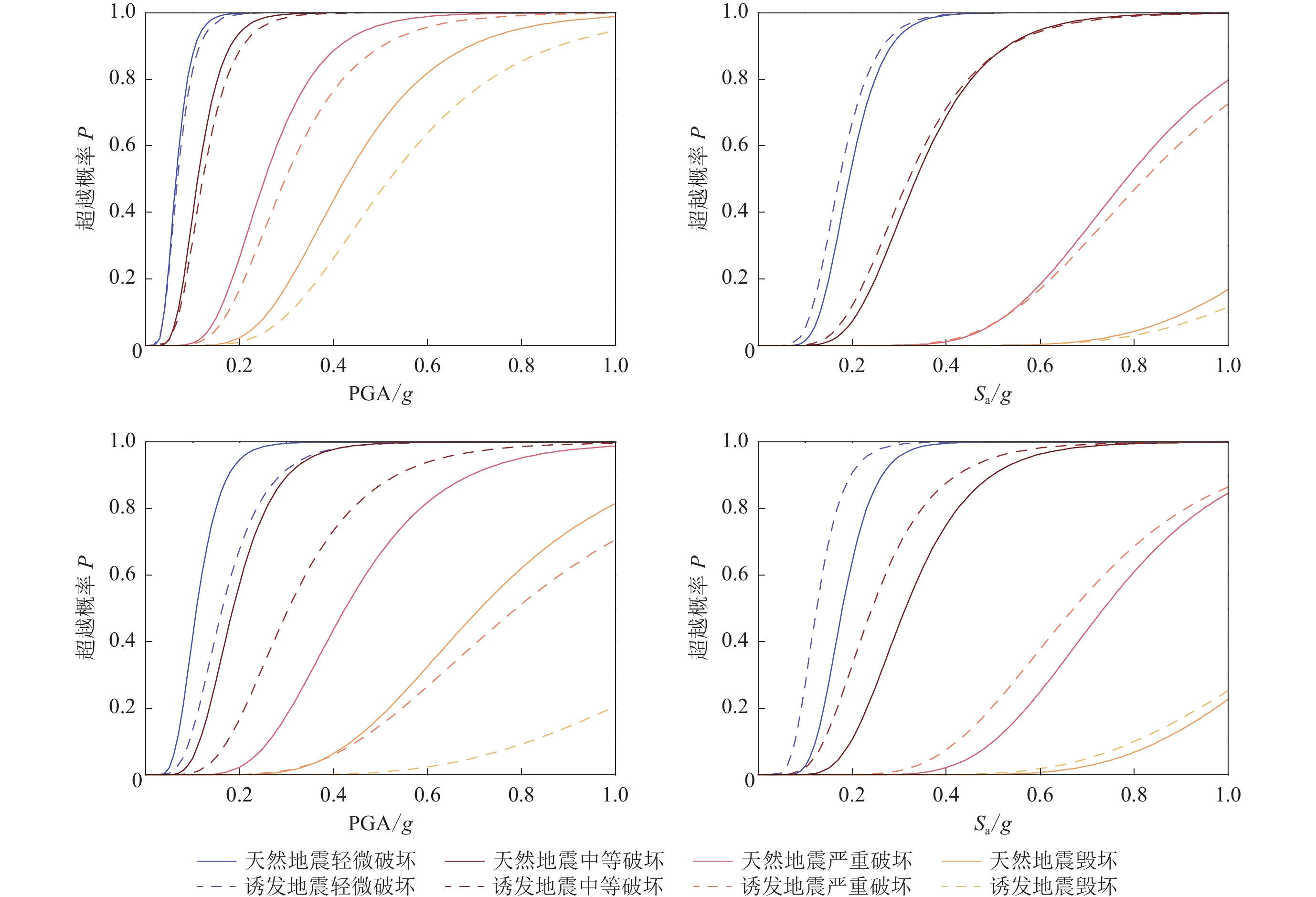
基于结构概率地震需求模型和结构破坏准则，以PGA和结构基本周期对应的加速度反应谱值Sa为输入地震动参数，建立诱发地震和天然地震作用下三层砌体结构和六层砌体结构的易损性曲线，如图8所示。
![]()
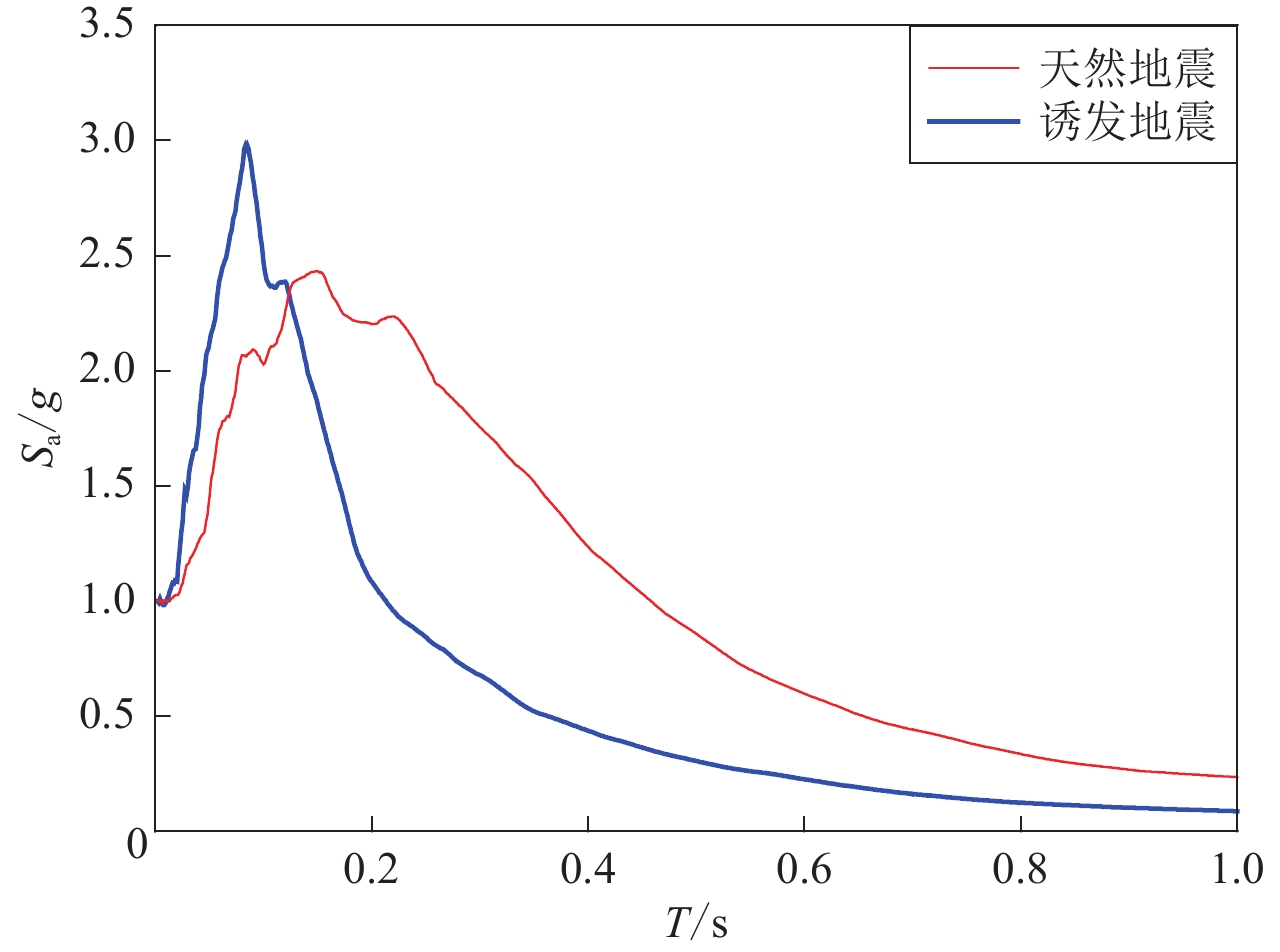
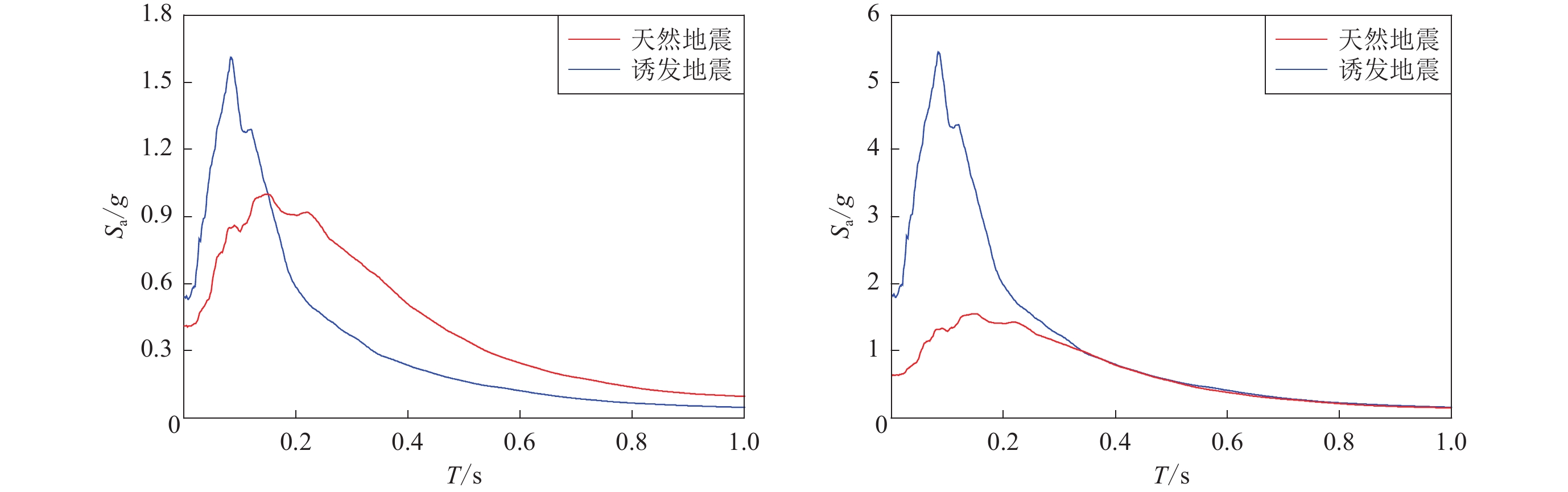
图 8 三层（上）、六层（下）砌体结构基于PGA （a）和Sa （b）的易损性曲线Figure 8. Vulnerability curves of three-storey （top） and six-storey （bottom） masonry structures based on PGA （a） and Sa （b）从图8中可以看出，当采用PGA表征地震动的强度水平建立易损性曲线时，以天然地震地震动作为输入的易损性均高于诱发地震，即对应于相同的PGA值，天然地震地震动作用下结构各破坏状态的超越概率均大于诱发地震，其中以六层砌体结构严重破坏和毁坏状态最为显著。也就是说，采用天然地震作用下基于PGA的结构易损性模型评估考虑诱发地震影响的灾害风险偏保守。图9给出了天然地震和诱发地震的地震动对PGA归一化处理后的加速度反应谱平均值。显然，在峰值加速度相同的情况下，天然地震地震动在三层结构基本自振周期0.15 s和六层结构基本自振周期0.34 s的加速度反应谱平均值均大于诱发地震的情况，特别是在0.34 s处非常显著。对于基本振型反应为主导的三层和六层砌体结构，天然地震地震动和诱发地震地震动上述频谱特性的差异是导致结构易损性差异的主要原因。
![]()
图 9 基于PGA归一化后的天然地震和诱发地震的平均地震动加速度反应谱Figure 9. Mean ground motion acceleration response spectra of natural and induced earthquakes after PGA normalization从图8还可以看出：当采用结构基本自振周期的加速度反应谱Sa表征地震动强度水平建立易损性曲线时，以天然地震地震动和诱发地震地震动作为输入得到的三层砌体结构易损性曲线比较接近，即对应于相同的Sa值，天然地震地震动作用下结构基本完好和轻微破坏的超越概率大致与诱发地震的情况相同，而严重破坏和毁坏的超越概率略大于诱发地震。图10a给出了天然地震和诱发地震的地震动对Sa （0.15 s）归一化处理后的加速度反应谱平均值，可以看到，天然地震地震动的平均加速度反应谱在大于0.15 s的周期段仍大于诱发地震地震动，而这些频率成分影响着结构软化基本周期延长后的地震响应。
![]()
图 10 基于Sa （0.15 s）（a）和Sa （0.34 s）（b）归一化后的天然地震与诱发地震的平均地震动加速度反应谱Figure 10. Mean ground motion acceleration response spectra of natural earthquakes and induced earthquakes after Sa （0.15 s）（a） and Sa （0.34 s）（b） normalization从图8也可以看出，当采用结构基本自振周期的加速度反应谱Sa表征地震动的强度水平建立易损性曲线时，以天然地震地震动作为输入得到的六层砌体结构易损性低于诱发地震的情况，即对应于相同的Sa值，诱发地震地震动作用下结构各破坏状态的超越概率均大于天然地震。图10b给出了天然地震和诱发地震的地震动对Sa （0.34 s）归一化处理后的加速度反应谱平均值，显然，天然地震和诱发地震的平均地震动加速度反应谱在大于0.34 s的周期段基本一致，而在小于0.34 s的周期段，天然地震的平均地震动加速度反应谱显著小于诱发地震。虽然六层砌体结构以基本振型反应为主导，但是高阶振型仍有一定的影响，而诱发地震地震动高频成分较天然地震地震动更为丰富，因此在相同Sa条件下，诱发地震地震动可能导致六层砌体结构产生更高的破坏概率。
可见，忽略天然地震地震动与诱发地震地震动的幅值及频谱特性之间的差异，采用基于天然地震地震动作为输入的结构易损性模型评估考虑诱发地震影响的地震灾害风险不尽合理，有必要建立考虑诱发地震影响的建筑结构易损性模型。
3.3 两次诱发地震作用下结构易损性分析
结构在单次诱发地震作用下会产生不同程度的损伤，多次诱发地震后材料、构件、结构损伤逐渐累积，最终会导致结构失效，因此只考虑单次诱发地震对结构的作用是不完善、不安全的。本文采用循环往复加载分析方法（黄维等，2011；刘晶波等，2013），分析两次诱发地震的地震动作用对砌体结构的影响。在使用Pushover计算出结构最大顶点位移之后，先正向加载到结构在第一次诱发地震地震动作用中的最大顶点位移，然后卸载到零，再反向对结构进行加载后卸载，再次加载直到结构破坏。将第二次正向加载曲线的坐标变换后得到结构第二次地震动作用的Pushover曲线，通过Pushover分析即可得到两次诱发地震地震动作用下的结构反应。
将选取的40组诱发地震地震动归一化处理后等间距调幅，调幅步长为0.05g，随机组合模拟两次诱发地震的作用。对砌体结构模型进行循环往复加载分析，以PGA作为地震动强度参数，计算结构在给定地震动强度参数下的结构延性系数，而后对所计算出的地震延性系数与地震动强度参数PGA进行对数线性回归拟合，得到诱发地震下砌体结构的概率地震需求模型。
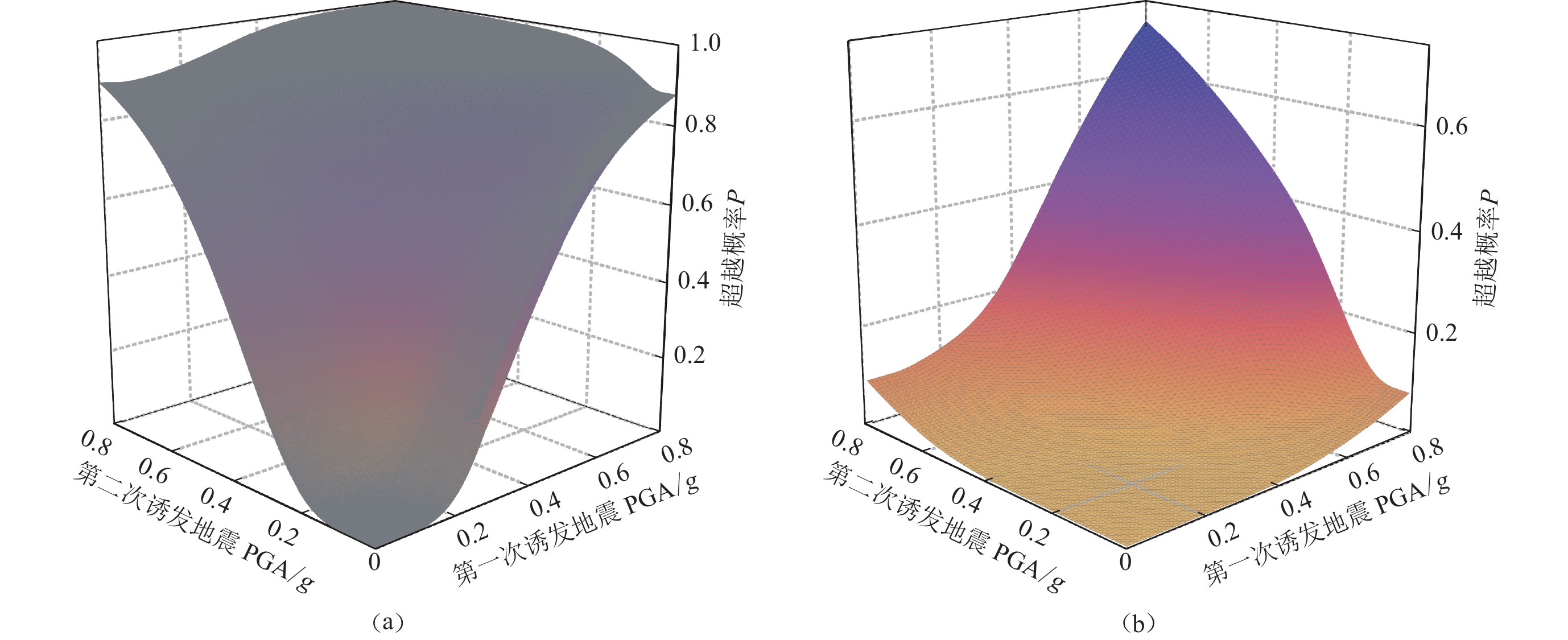
基于结构概率地震需求模型和结构破坏准则，建立基于PGA的砌体结构诱发地震易损性曲面，如图11所示。可见，随着第一次与第二次地震PGA的增加，砌体结构发生破坏的超越概率逐渐增大。从两次诱发地震毁坏破坏图可以看出，在两次诱发地震的地震动作用下，结构不同状态的破坏概率并不关于第一次与第二次地震PGA相等的平面对称，结构在第一次地震大第二次地震小情况下比第一次地震小第二次地震大情况下的破坏概率大，这是由于结构损伤程度随地震强度增大而增大，结构的性能状态发生变化，承载能力与抗震能力下降，结构可靠度降低。图11中易损面与只发生第一次诱发地震的平面的交线即为单次诱发地震作用下砌体结构破坏的超越概率，可以看出，相比单次地震作用，砌体结构在两次地震作用下结构产生不同破坏状态的概率显著增大。
![]()
图 11 两次诱发地震作用下三层（a）、六层（b）砌体结构毁坏的易损面Figure 11. Vulnerable surfaces of three-story （a） and six-story （b） masonry structure collapse under two induced earthquakes4. 结论
本文综合考虑诱发地震的地震动特性和建筑结构特征，以典型砌体结构为研究对象，分别选取天然地震和诱发地震的加速度时程作为输入，采用Pushover方法开展结构地震响应和易损性分析研究，得出以下结论：
1） 震级和震中距都接近时，诱发地震地震动的高频成分相对天然地震更丰富，对自振周期在0.1 s左右的短周期结构可能造成更严重的破坏。
2） 建立了诱发地震和天然地震地震动作用下基于峰值加速度和结构基本周期加速度反应谱的砌体结构易损性曲线，结果表明诱发地震地震动与天然地震地震动作用下的结构地震响应及易损性曲线均有显著差异。无论采用PGA还是Sa作为地震动参数，以天然地震地震动作用下的结构易损性模型开展风险评估都可能导致偏不安全的结果。因此，需要建立以诱发地震地震动作为输入的结构易损性模型，以考虑诱发地震地震动特性的影响。
3） 连续两次诱发地震作用下的易损性分析结果表明，重复诱发地震作用会导致结构承载能力降低，结构在各破坏状态下的超越概率相对单次地震的地震动作用显著增加。
建立考虑诱发地震影响的典型结构易损性模型，是页岩气开采区地震灾害风险评估和防控的关键内容，对我国推进页岩气大规模开发、解决能源周期性不足的问题具有十分现实的意义。但目前我国页岩气开采区强震记录数量有限，随着诱发地震强震记录数量的增加，诱发地震地震动特性及其对我国典型建筑结构影响方面的研究将会有更深入的进展。
-
![]()
图 3 砌体结构层间剪切模型示意图
Figure 3. Schematic diagram of interlayer shearing model of masonry structure
![]()
图 4 三线性恢复力模型示意图（张令心等，2002）
Figure 4. Schematic diagram of trilinear restoring of masonry structure force model （after Zhang et al，2002）
![]()
图 5 诱发地震（a）和天然地震（b）的地震动加速度反应谱
Figure 5. Ground motion acceleration response spectra of induced earthquake （a） and natural earthquake （b）
![]()
图 6 诱发地震与天然地震的平均地震动加速度反应谱
Figure 6. Mean ground motion acceleration response spectra of induced and natural earthquakes
![]()
图 7 诱发地震（a）与天然地震（b）的三层结构地震概率需求模型
Figure 7. Probabilistic seismic demand models of three-story structure for induced earthquakes （a） and natural earthquakes （b）
![]()
图 8 三层（上）、六层（下）砌体结构基于PGA （a）和Sa （b）的易损性曲线
Figure 8. Vulnerability curves of three-storey （top） and six-storey （bottom） masonry structures based on PGA （a） and Sa （b）
![]()
图 9 基于PGA归一化后的天然地震和诱发地震的平均地震动加速度反应谱
Figure 9. Mean ground motion acceleration response spectra of natural and induced earthquakes after PGA normalization
![]()
图 10 基于Sa （0.15 s）（a）和Sa （0.34 s）（b）归一化后的天然地震与诱发地震的平均地震动加速度反应谱
Figure 10. Mean ground motion acceleration response spectra of natural earthquakes and induced earthquakes after Sa （0.15 s）（a） and Sa （0.34 s）（b） normalization
![]()
图 11 两次诱发地震作用下三层（a）、六层（b）砌体结构毁坏的易损面
Figure 11. Vulnerable surfaces of three-story （a） and six-story （b） masonry structure collapse under two induced earthquakes
表 1 砌体结构延性系数与破坏等级之间的关系（郝敏等，2007）
Table 1 Relationship between ductility coefficient and damage grade of masonry structure （Hao et al，2007）
破坏等级 延性系数μ 能力参数限值 基本完好 μ≤0.68 轻微破坏 0.68＜μ≤1.3 0.68 中等破坏 1.3＜μ≤3.5 1.3 严重破坏 3.5＜μ≤6.5 3.5 毁坏 μ＞6.5 6.5 
下载: 导出CSV
表 2 砌体墙段开洞影响系数
Table 2 Influence coefficient of masonry wall with opening
开洞率 影响系数φ0 开洞率 影响系数φ0 0.9 0.98 0.6 0.76 0.8 0.94 0.5 0.68 0.7 0.88 0.4 0.56
下载: 导出CSV
表 3 天然地震地震动与诱发地震地震动记录的基本信息
Table 3 Basic information of ground motion records of natural and induced earthquakes
诱发地震 天然地震 诱发地震 天然地震 M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
/（cm·s−2）M 震中距
/kmPGA
/（cm·s−2）4.7 12.95 14.04 4.79 13.55 38.97 4.9 31.4 27.71 4.92 31.71 30.24 4.7 2.71 63.94 4.7 2.84 158.0 4.9 15.02 69.84 4.92 14.94 38.79 5.7 27.29 62.39 5.7 27.78 36.42 4.3 3.95 197.5 4.27 3.69 20.02 4.8 27.63 63.60 4.88 27.89 103.6 4.4 6.02 231.6 4.45 6.46 33.72 4.5 5.17 36.20 4.6 5.2 184.5 4.5 7.28 43.7 4.45 7.46 63.36 4.5 10.04 19.55 4.6 10.16 12.10 4.1 2.0 261.5 4.12 1.42 167.51 4.5 4.47 367.8 4.45 4.7 29.43 4.1 4.23 97.21 4.1 4.41 99.87 4.3 2.47 215.5 4.27 2.67 48.83 4.4 6.71 114.9 4.37 6.48 6.004 4.3 5.66 267.6 4.3 5.28 37.54 4.4 4.9 162.1 4.45 4.7 29.44 4.1 2.76 284.6 4.05 2.93 21.93 4.4 1.7 341.5 4.45 1.0 159.68 4.1 5.42 380.0 4.1 5.39 84.58 4.4 4.53 116.1 4.5 4.62 57.93 4.4 2.88 152.7 4.45 2.38 216.77 4.7 27.22 49.30 4.77 26.39 8.036 4.3 8.57 154.4 4.2 8.32 54.57 4.4 6.9 38.51 4.5 6.35 26.75 4.3 8.55 144.4 4.3 8.76 68.84 4.7 23.32 30.87 4.7 23.47 15.42 4.3 2.48 666.5 4.3 2.67 48.83 4.7 16.2 51.80 4.7 16.05 16.94 4.3 6.96 51.38 4.26 7.34 14.54 4.3 3.39 255.1 4.26 3.45 44.97 4.9 17.91 72.05 4.9 18.46 26.19 4.2 3.68 284.8 4.2 3.34 71.14 4.9 24.25 47.49 4.92 24.5 36.80 4.2 7.92 33.5 4.2 7.98 120.56 4.9 28.69 37.40 4.92 29 59.15 4.2 5.52 19.80 4.3 5.14 24.57 4.9 21.21 37.72 4.9 21.48 28.98 4.2 5.84 413.7 4.2 5.31 245.06
下载: 导出CSV
表 4 不同地震及结构类型关于PGA和Sa的拟合参数
Table 4 Fitting parameters of different seismic and structural types
结构类型 地震类型 地震动参数 拟合结果 拟合优度 均方根误差 三层砌体 诱发地震 PGA lnDM＝1.11 lnPGA＋2.60 0.78 0.62 天然地震 PGA lnDM＝1.20 lnPGA＋2.90 0.71 0.56 诱发地震 Sa lnDM＝1.05 lnSa＋1.46 0.84 0.36 天然地震 Sa lnDM＝1.17 lnSa＋1.54 0.77 0.50 六层砌体 诱发地震 PGA lnDM＝1.04 lnPGA＋1.50 0.73 0.55 天然地震 PGA lnDM＝1.20lnPGA＋2.28 0.81 0.51 诱发地震 Sa lnDM＝0.97lnSa＋1.64 0.63 0.71 天然地震 Sa lnDM＝1.16lnSa＋1.61 0.64 0.69 注：DM为结构延性系数。
下载: 导出CSV
-
郝敏,谢礼立,李伟. 2007. 基于砌体结构破坏损伤的地震烈度物理标准研究[J]. 地震工程与工程振动,27(5):27–32. Hao M,Xie L L,Li W. 2007. Study on physical measure of seismic intensity based on damage to masonry structures[J]. Earthquake Engineering and Engineering Vibration,27(5):27–32 (in Chinese).
何登发,鲁人齐,黄涵宇,王晓山,姜华,张伟康. 2019. 长宁页岩气开发区地震的构造地质背景[J]. 石油勘探与开发,46(5):993–1006. He D F,Lu R Q,Huang H Y,Wang X S,Jiang H,Zhang W K. 2019. Tectonic and geological background of the earthquake hazards in Changning shale gas development zone,Sichuan basin,SW China[J]. Petroleum Exploration and Development,46(5):993–1006 (in Chinese).
黄维,钱江,庄彬彬. 2011. 基于两次推覆分析考虑损伤效应的结构抗震性能评估[J]. 结构工程师,27(5):111–115. Huang W,Qian J,Zhuang B B. 2011. Seismic performance analysis of structures considering damage effect based on twice Pushover analysis[J]. Structural Engineers,27(5):111–115 (in Chinese).
刘晶波,王文晖,赵冬冬,张小波. 2013. 循环往复加载的地下结构Pushover分析方法及其在地震损伤分析中的应用[J]. 地震工程学报,35(1):21–28. Liu J B,Wang W H,Zhao D D,Zhang X B. 2013. Pushover analysis method of underground structures under reversal load and its application in seismic damage analysis[J]. China Earthquake Engineering Journal,35(1):21–28 (in Chinese).
缪志伟,马千里,叶列平,陆新征. 2008. Pushover方法的准确性和适用性研究[J]. 工程抗震与加固改造,30(1):55–59. Miao Z W,Ma Q L,Ye L P,Lu X Z. 2008. Study on the accuracy and applicability of the Pushover analysis[J]. Earthquake Resistant Engineering and Retrofitting,30(1):55–59 (in Chinese).
叶列平,马千里,缪志伟. 2009. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动,29(4):9–22. Ye L P,Ma Q L,Miao Z W. 2009. Study on earthquake intensities for seismic analysis of structures[J]. Journal of Earthquake Engineering and Engineering Vibration,29(4):9–22 (in Chinese).
张令心,江近仁,刘洁平. 2002. 多层住宅砖房的地震易损性分析[J]. 地震工程与工程振动,22(1):49–55. Zhang L X,Jiang J R,Liu J P. 2002. Seismic vulnerability analysis of multistory dwelling brick buildings[J]. Earthquake Engineering and Engineering Vibration,22(1):49–55 (in Chinese).
张勇. 2013. RC框架结构Pushover分析方法顶点位移的概率研究[D]. 长沙: 湖南大学: 8–28. Zhang Y. 2013. Probability Analysis of Top Displacement for Pushover Analysis Method of RC Frame Structure[D]. Changsha: Hunan University: 8−28 （in Chinese）.
Assatourians K,Atkinson G M. 2019. Processed ground-motion records from induced earthquakes for use in engineering applications[J]. Can J Civil Eng,47(1):96–108.
Chase R E,Liel A B,Luco N,Baird B W. 2019. Seismic loss and damage in light-frame wood buildings from sequences of induced earthquakes[J]. Earthq Eng Struct Dyn,48(12):1365–1383. doi: 10.1002/eqe.3189
Cornell C A,Jalayer F,Hamburger R O,Foutch D A. 2002. Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines[J]. J Struct Eng,128(4):526–533. doi: 10.1061/(ASCE)0733-9445(2002)128:4(526)
Crowley H,Pinho R,Polidoro B,Van Elk J. 2017. Developing fragility and consequence models for buildings in the Groningen field[J]. Neth J Geosci,96(5):S247–S257.
Crowley H,Pinho R,Van Elk J,Uilenreef J. 2019. Probabilistic damage assessment of buildings due to induced seismicity[J]. Bull Earthq Eng,17(8):4495–4516. doi: 10.1007/s10518-018-0462-1
Da Silva A H A,Pereira E M V,Pita G L,Siqueira G H,Vieira Jr L C M. 2021. Damage estimation in reinforced concrete buildings from induced earthquakes in Brazil[J]. Eng Struct,234(1):111904.
Kallioras S,Graziotti F,Penna A. 2019. Numerical assessment of the dynamic response of a URM terraced house exposed to induced seismicity[J]. Bull Earthq Eng,17(3):1521–1552. doi: 10.1007/s10518-018-0495-5
Kurkowski J L. 2018. Seismic Vulnerability of Masonry Facades in Texas and Oklahoma Regions[D]. Austin: The University of Texas: 1−86.
Mulder M, Perey P. 2018. Gas production and earthquakes in Groningen: Reflection on economic and social consequences[C]//41st International Conference of the International Association for Energy Economics. Groningen, Netherlands: Centre for Energy Economics Research, University of Groningen: 69.
Shome N. 1999. Probabilistic Seismic Demand Analysis of Nonlinear Structures[D]. Stanford: Stanford University: 45−192.
Walsh F R,Zoback M D. 2015. Oklahoma’s recent earthquakes and saltwater disposal[J]. Sci Adv,1(5):e1500195. doi: 10.1126/sciadv.1500195
Yang H F,Zhou P C,Fang N,Zhu G H,Xu W B,Su J R,Meng F B,Chu R S. 2020. A shallow shock:The 25 February 2019 ML4.9 earthquake in the Weiyuan shale gas field in Sichuan,China[J]. Seismol Res Lett,91(6):3182–3194. doi: 10.1785/0220200202
计量
- 文章访问数: 219
- HTML全文浏览量: 47
- PDF下载量: 60
