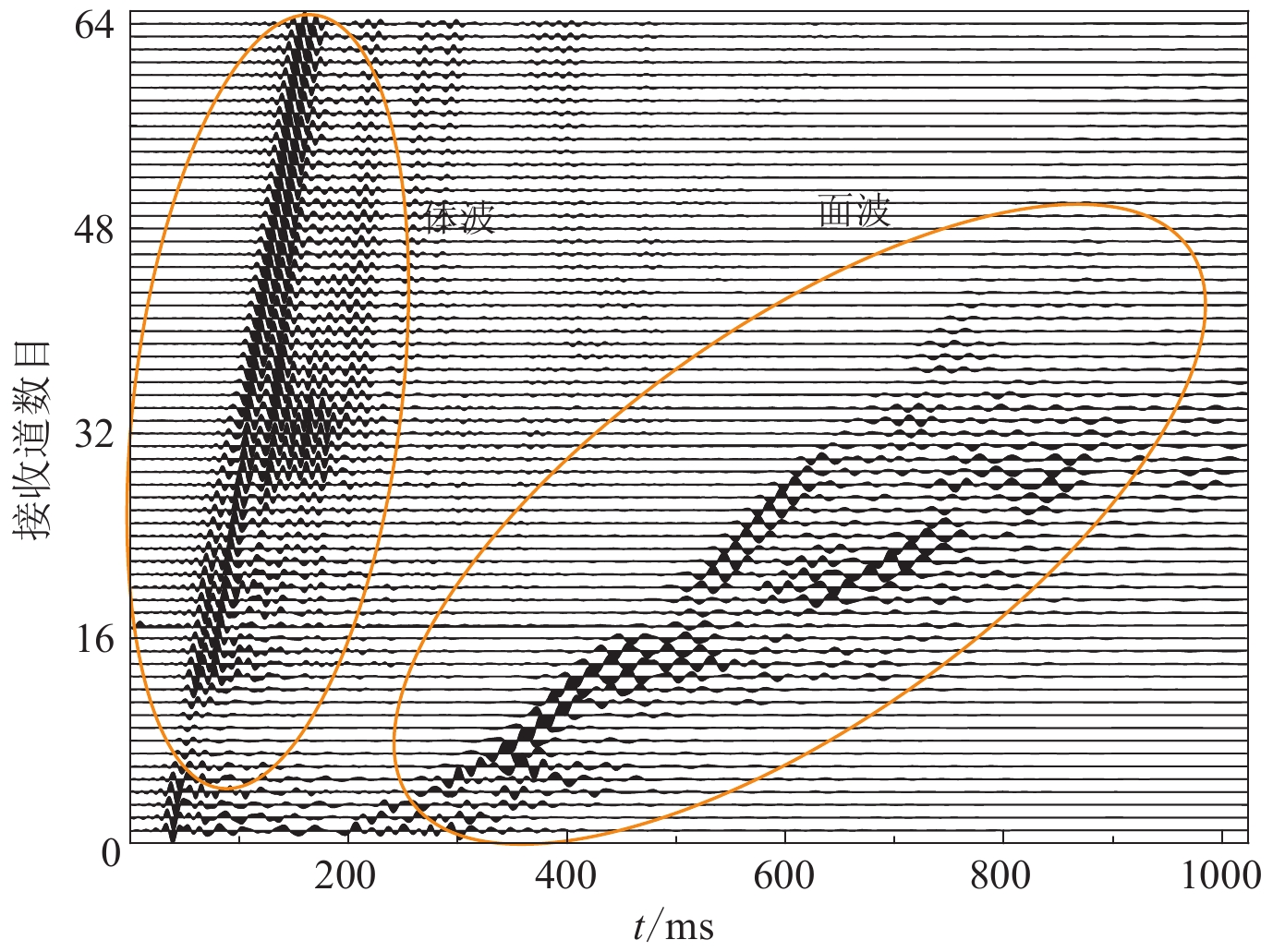
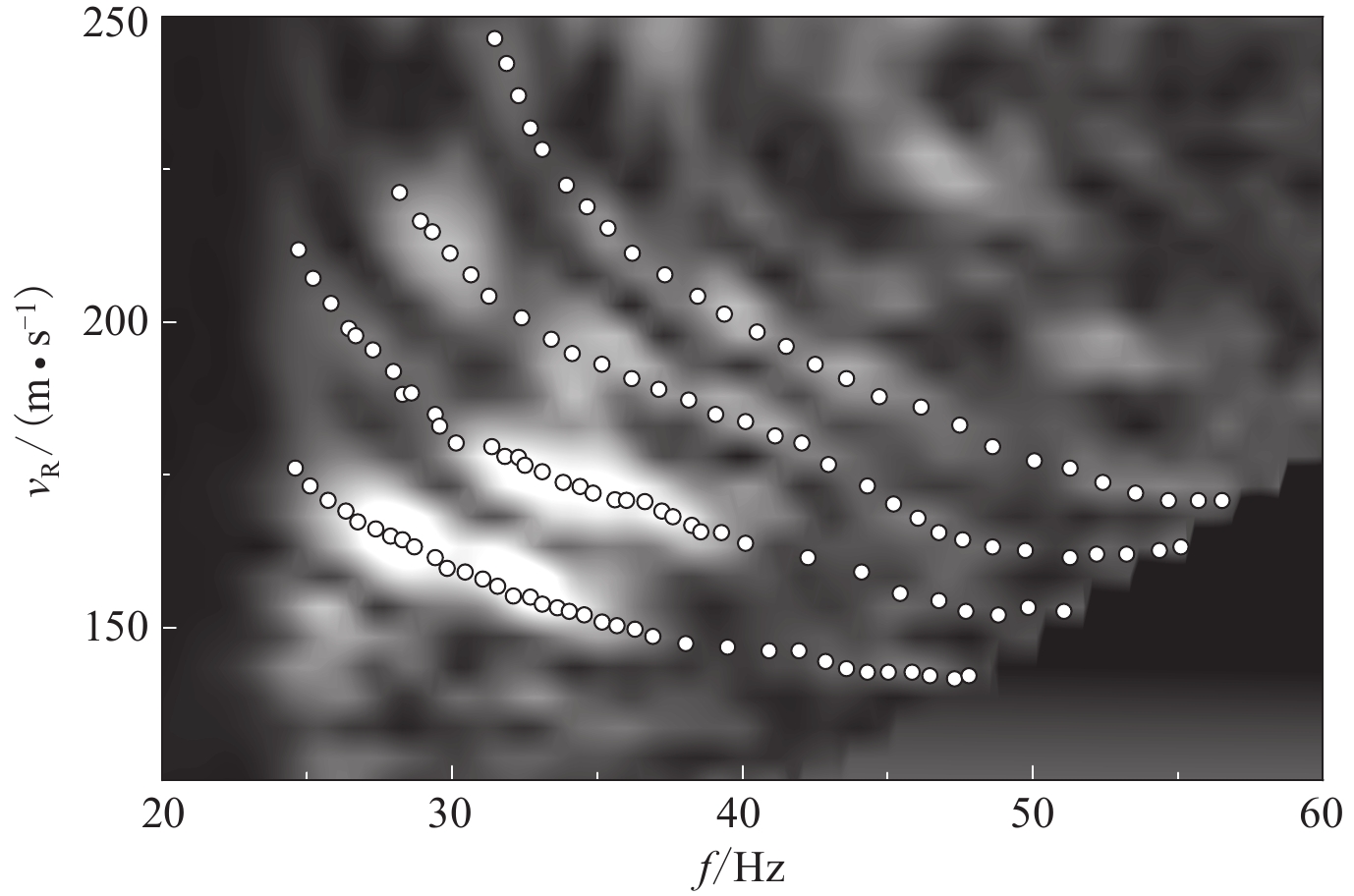
Inversion of multi-mode surface waves extracted from the shallow seismic reflection data
-
摘要: 浅层地震反射波法和面波方法是两种相互独立发展的地震勘探方法，在各自的数据采集和处理中，对方都是作为干扰信号而存在. 本文利用浅层地震反射资料中被视为干扰的面波信号，通过成熟的多道面波勘探技术处理浅层地震反射资料，在频率-波数域中提取多阶振型面波的频散曲线，并基于该曲线反演浅地表S波速度结构. 这种方法充分开发利用了已有数据，无需单独的面波数据采集系统，同时为解释浅层地震反射资料提供了额外的信息约束. 结果表明：浅层地震反射资料中可提取出可靠的多阶振型面波频散曲线，并能给出稳定的反演结果，同时，面波反演的多解性可以通过高阶振型反演得以进一步约束；低速层的存在是观测频散曲线出现振型跳跃或呈“之”字形回折的必要条件而非充分条件.Abstract: Shallow seismic reflection and surface wave are two seismic exploration methods which are developing independently. In their respective data collection and processing, the concerned signal in one method is usually thought as the disturbed one in the other method. In this paper, the " disturbed” surface wave occurred in the data collected by shallow seismic reflection survey was reused. The dispersion curves of multi-mode surface waves were extracted in the frequency-wave number domain based on these data by applying the multi-channel surface wave technology. The S-wave velocity profiles were then inversed by taking the fundamental and/or first-order modes into account. This method fully exploited the existing data. Therefore, the special data collection for surface waves is not needed, and additional constraint is offered to the interpretation of shallow seismic reflection data. The results indicate that the reliable multi-mode dispersion curves of surface waves can be extracted from the shallow seismic reflection data, and stable S-wave velocity profile can be obtained. Meanwhile, it is concluded that the existence of low-velocity layer is the necessary rather than the sufficient condition to make the observed dispersion curve exhibit the mode-jumping among the mode branches.
-
引言
2015年4月25日尼泊尔中东部郎塘地区（Lamjung）发生MS8.1地震，根据美国地质调查局（USGS，2015）发布的地震监测信息，该地震震中位于（28.1°N，84.7°E），震源深度为15 km.
强震的发生能够造成大区域地壳形变，引起强烈的重力变化（Imanishi et al，2004 ）. 许多研究结果已从理论上证实GRACE卫星能够检测到M≥8.0地震引起的重力变化（Gross，Chao，2001；Mikhailov et al，2004 ；Sun，Okubo，2004）. Han等（2006）首次利用GRACE星间跟踪数据提取出2004年苏门答腊MW9.3地震断层错动引起的“正—负”重力变化异常信号. 随后，众多研究人员对GRACE检测强震重力变化的能力进行了研究（De Linage et al，2009 ；周新等，2011；Matsuo，Heki，2011）. Li和Shen （2011）发现重力梯度的北向分量对GRACE观测到的“南北条带”误差具有较强的压制作用，并提取了水平向同震重力梯度变化的“正—负—正”空间分布特征. Wang等（2012）利用GRACE月重力场模型提取了苏门答腊地震重力梯度变化的详细过程，其结果与同震滑动模型预测的结果相一致. 初步研究表明，尼泊尔MS8.1地震前区域重力变化具有异常现象（邹正波等，2015）. 随着GRACE数据的更新及数据处理方法的改进，有必要利用更长时段的数据进行深入地研究，本文针对GRACE数据处理中由滤波方法造成的信号衰减问题，利用地震前后的GRACE RL05数据研究尼泊尔MS8.1地震震区及邻近区域北向重力场梯度时空变化特征，并结合黏弹性分层位错模型模拟该地震北向重力梯度的同震变化，对研究区北向重力梯度的精度进行讨论，分析GRACE检测尼泊尔地震北向重力梯度同震变化的可能性，为研究该地震的孕育和发震机理探索新的方法.
1. 区域构造背景
尼泊尔MS8.1地震发生于喜马拉雅碰撞造山带中段，震源机制解（Yagi，Okuwaki，2015；杨晓平等，2016）表明该地震为低角度逆冲型. 喜马拉雅碰撞造山带属于青藏高原南边界，青藏高原形成于印度板块与欧亚板块陆陆俯冲碰撞和推挤作用下，高原物质在这种挤压力和重力的共同作用下向四周运移，同时，高原物质在东流过程中，受到华北和华南等高强度地块的阻挡，在青藏高原东缘形成了局部挤压推覆构造带及前陆盆地系统（徐锡伟等，2008）.
GPS数据显示印度板块以大约50 mm/a的速度向欧亚板块俯冲，在喜马拉雅弧汇聚速度达到20 mm/a，应力异常集中，形成喜马拉雅地震带（邓起东等，2014），历史上沿该地震带发生过多次大地震（Prajapati et al，2013 ；Shah，2013；Mittal，Kumar，2015），此次尼泊尔MS8.1地震便位于此，该地震是由欧亚板块与印度板块持续地南北向俯冲挤压逆冲造成的. 图1给出了尼泊尔及其邻近区域的地形和主要断层以及2008—2015年MS≥7.0地震的分布情况.
![]()
图 1 尼泊尔及其邻近区域地形及2008—2015年MS≥7.0地震分布Figure 1. Topography and distribution of MS≥7.0 earthquakes in Nepal and its vicinity areas from 2008 to 20152. 数据与方法
This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$\Delta g\left( {\theta ,\lambda } \right) = \frac{{{ G}M}}{{{a^2}}} \sum\limits_{l = 2}^N {\left( {l + 1} \right)\sum\limits_{m = 0}^l {\left[ {\Delta {{\overline C}\, ^m_{l}}\cos \left( {m\lambda } \right) + \Delta {{\overline S}\, ^m_{l}}\sin \left( {m\lambda } \right)} \right]{{{\overline P}}\,_{l}\,\!\!\!^m}\left( {\cos \theta } \right)} } ,$
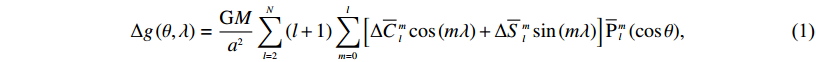
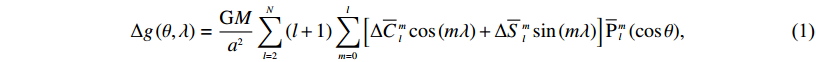
(1) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
在球面上任一点建立局部直角坐标系，x轴指向北，y轴指向东，z轴向下指向球心. 基于式（1），可得重力梯度变化在3个坐标轴方向上的分量（Li，Shen，2011），即
$\Delta {g_x}\left( {\theta ,\lambda } \right) = \frac{{{ G}M}}{{{a^3}}} \sum\limits_{l = 2}^N {\left( {l + 1} \right)\sum\limits_{m = 0}^l {[\Delta {{\overline C}\ \! ^m_{l}}\cos (m\lambda ) + \Delta {{\overline S}\ \!\!^m_{l}}\sin (m\lambda )] \frac{{{{d}}[{{\overline { P}}\,_{l}\!\!\!\,^m}\left( {\cos \theta } \right)]}}{{{{d}}\theta }}} } ,$
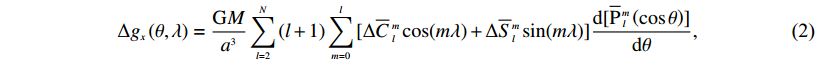
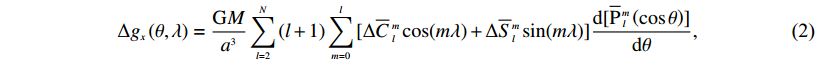
(2) $\Delta {g_y}\left( {\theta ,\lambda } \right) = \frac{{{ G}M}}{{{a^3}}} \sum\limits_{l = 2}^N {\left( {l + 1} \right)\sum\limits_{m = 0}^l {m[ - \Delta {{\overline C}\ \!\!^m_{l}}\sin (m\lambda ) + \Delta {{\overline S}\ \!\!^m_{l}}\cos (m\lambda )] \frac{{{{\overline { P}}\,_{l}\,\!\!\!^m}\left( {\cos \theta } \right)}}{{\sin \theta }}} } ,$
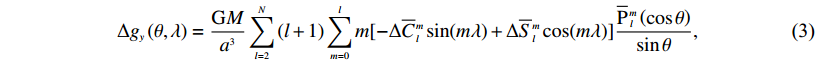
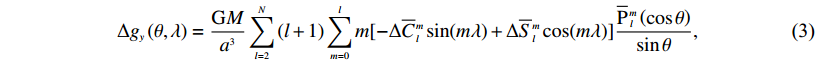
(3) $\Delta {g_z}\left( {\theta ,\lambda } \right) = \frac{{{ G}M}}{{{a^3}}} \sum\limits_{l = 2}^N {\left( {l + 1} \right)(l + 2)\sum\limits_{m = 0}^l {[\Delta {{\overline C}\ \!^m_{l}}\cos (m\lambda ) + \Delta {{\overline S}\ \!\!^m_{l}}\sin (m\lambda )] {{\overline { P}}\,_{l}\!\!\!\,^m}\left( {\cos \theta } \right)} } ,$
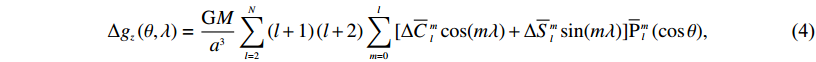
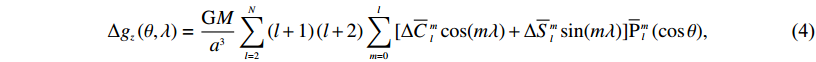
(4) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$\frac{{{{d}}[{{\overline { P}}\,_{l}\,\!\!\!^m}\left( {\cos \theta } \right)]}}{{{{d}}\theta }} = a_{lm}^1{\overline { P}\,\,\,_{l}\,\!\!\!\!\!^{m-1}}\left( {\cos \theta } \right) + a_{lm}^2{\overline { P}\,\,\,_{l}\,\!\!\!\!\!^{m+1}}\left( {\cos \theta } \right),$
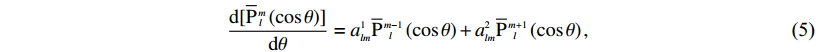
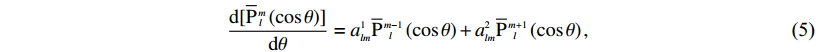
(5) $a_{lm}^1 = \frac{1}{2}\sqrt {l + m} \sqrt {l - m + 1} \sqrt {\frac{{2 - {\delta _{m,\;0}}}}{{2 - {\delta _{m - 1,\;0}}}}} ,$
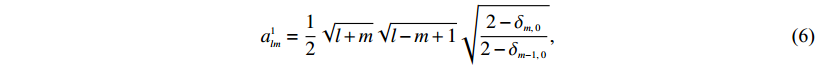
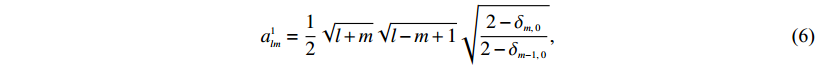
(6) $a_{lm}^2 = - \frac{1}{2}\sqrt {l - m} \sqrt {l + m + 1} \sqrt {\frac{{2 - {\delta _{m,\;0}}}}{{2 - {\delta _{m + 1,\;0}}}}}{\text{.}}$
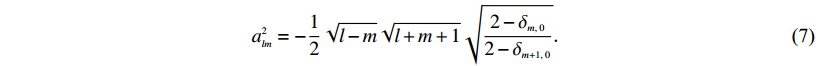
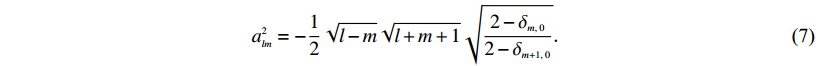
(7) This page contains the following errors:
error on line 1 at column 1: Start tag expected, '<' not foundBelow is a rendering of the page up to the first error.
$\frac{{m{{\overline { P}}\,_{l}\,\!\!\!^m}\left( {\cos \theta } \right)}}{{\sin \theta }} = b_{lm}^1{\overline { P}\,\,_{l - 1}\ \!\!\!\!\!\!\!\!\!\! ^{m-1}}\left( {\cos \theta } \right) + b_{lm}^2{\overline{ P}\,\,_{l + 2}\ \!\!\!\!\!\!\!\!\!\!^{m+2}}\left( {\cos \theta } \right)\;,\quad\quad m \ne 0\ ,$
(8) $b_{lm}^1 = \frac{1}{2}\sqrt {l + m} \sqrt {l + m - 1} \sqrt {\frac{{\left( {2 - {\delta _{m,\;0}}} \right)\left( {2l + 1} \right)}}{{\left( {2 - {\delta _{m - 1,\;0}}} \right)\left( {2l - 1} \right)}}} \ ,$
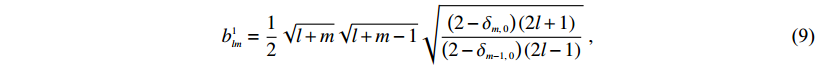
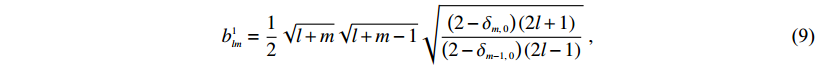
(9) $b_{lm}^2 = \frac{1}{2}\sqrt {l - m} \sqrt {l - m - 1} \sqrt {\frac{{\left( {2 - {\delta _{m,\;0}}} \right)\left( {2l + 1} \right)}}{{\left( {2 - {\delta _{m - 1,\; 0}}} \right)\left( {2l - 1} \right)}}}\ {\text{.}}$
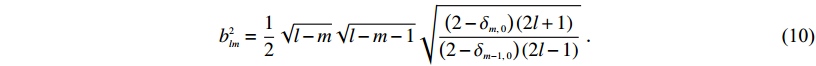
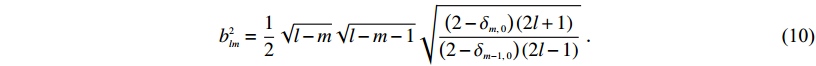
(10) 受卫星轨道误差、观测误差、模型及数据处理误差的影响，GRACE时变重力场在图像上表现出明显的“南北条带”，因此需选择一定的滤波以削弱重力场模型的噪声. 去相关滤波具有较好的去条带效果（Swenson，Wahr，2006），但在削弱误差的同时也会造成真实信号的衰减，而北向重力梯度对南北条带误差具有较强的压制作用，可以避免去相关滤波对真实信号的削弱（Li，Shen，2011）.
以2012—2014年月平均重力场为背景场，将2015年9月的重力场模型与其进行差分，之后采用300 km扇形滤波方法（Zhang et al，2009 ），得到重力及重力梯度3个分量的全球分布，结果如图2所示. 可以看出，重力梯度的3个分量包含了更多的细节变化信息，东向和垂向的南北条带更加明显，北向重力梯度的南北条带与重力场相比较弱，说明北向重力梯度对“南北条带”误差具有较好的压制作用，这源于GRACE任务K波段测距的设计特点使得测距系统对南北方向的重力变化相比其它方向更为敏感（高春春等，2015）.
![]()
图 2 与2012—2014年月平均重力场差分后得到的2015年9月全球重力变化Δg分布（a）及北向Δgx （b）、东向Δgy （c）和垂向Δgz （d）重力梯度变化分布Figure 2. The difference of global gravity change Δg （a） and gravity gradient change of north Δgx（b），east Δgy （c），and vertical Δgz （d） components from GRACE monthly data between September 2015 and the mean field from 2012 to 20143. 北向重力梯度时空分布特征
3.1 年度累积北向重力梯度变化
采用第2节中的方法，以2007年1—12月的平均重力场为背景场，将2008—2015年每年的月平均重力场与背景场进行差分（舍去2015年4月地震发生时段的数据），获得尼泊尔MS8.1地震震中周围区域的年度累积北向重力梯度，结果如图3所示.
![]()
图 3 尼泊尔及其邻近区域2008—2015年年度累积北向重力梯度Figure 3. Annual northern gravity gradient from 2008 to 2015 in Nepal and its vicinity areas（a） 2008；（b） 2009；（c） 2010；（d） 2011；（e） 2012；（f） 2013；（g） 2014；（h） 2015分析图3可知：① 北向重力梯度基本以地块边缘为界呈正负变化. 青藏地块东昆仑断裂带以南自2008年以来北向重力梯度增加比较明显，最大增幅为1.37×10−13/s2；青藏地块东北边界带的北向重力梯度异常逐渐向东迁移，2013年尤为明显，这可能与青藏高原物质东流有关（邓起东等，2014）；而西域地块、青藏高原东北缘及其与华南地块交界处以及印度板块北边界，北向重力梯度则出现明显下降；此外，缅甸地块、青藏地块、华南地块交界处的北向重力梯度在2011年之前缓慢增加，趋近于零，2011年之后有比较显著的减小. ② 尼泊尔MS8.1地震发生在北向重力梯度的零值线附近，与地面流动重力（祝意青等，2014）以及GRACE卫星重力（邹正波等，2015）的观测结果一致；此外，2008年新疆于田MS7.3地震、四川汶川MS8.0地震、2011年缅甸MS7.6地震和2014年新疆于田MS7.3地震均发生在北向重力梯度正负变化的零值线附近. ③ 在尼泊尔MS8.1地震前北向重力梯度异常变化比较明显，隆起区北向重力梯度增加，俯冲区北向重力梯度减小，隆起区和俯冲区北向重力梯度的峰值均出现在2014年，分别为1.26×10−13/s2和−1.84×10−13/s2，而2015年隆起区和俯冲区北向重力梯度的峰值分别为1.07×10−13/s2和−1.72×10−13/s2，与2014年相比均有所减小，可能与震后壳幔物质黏滞调整有关（De Linage et al，2009 ）.
3.2 点位北向重力梯度时间序列
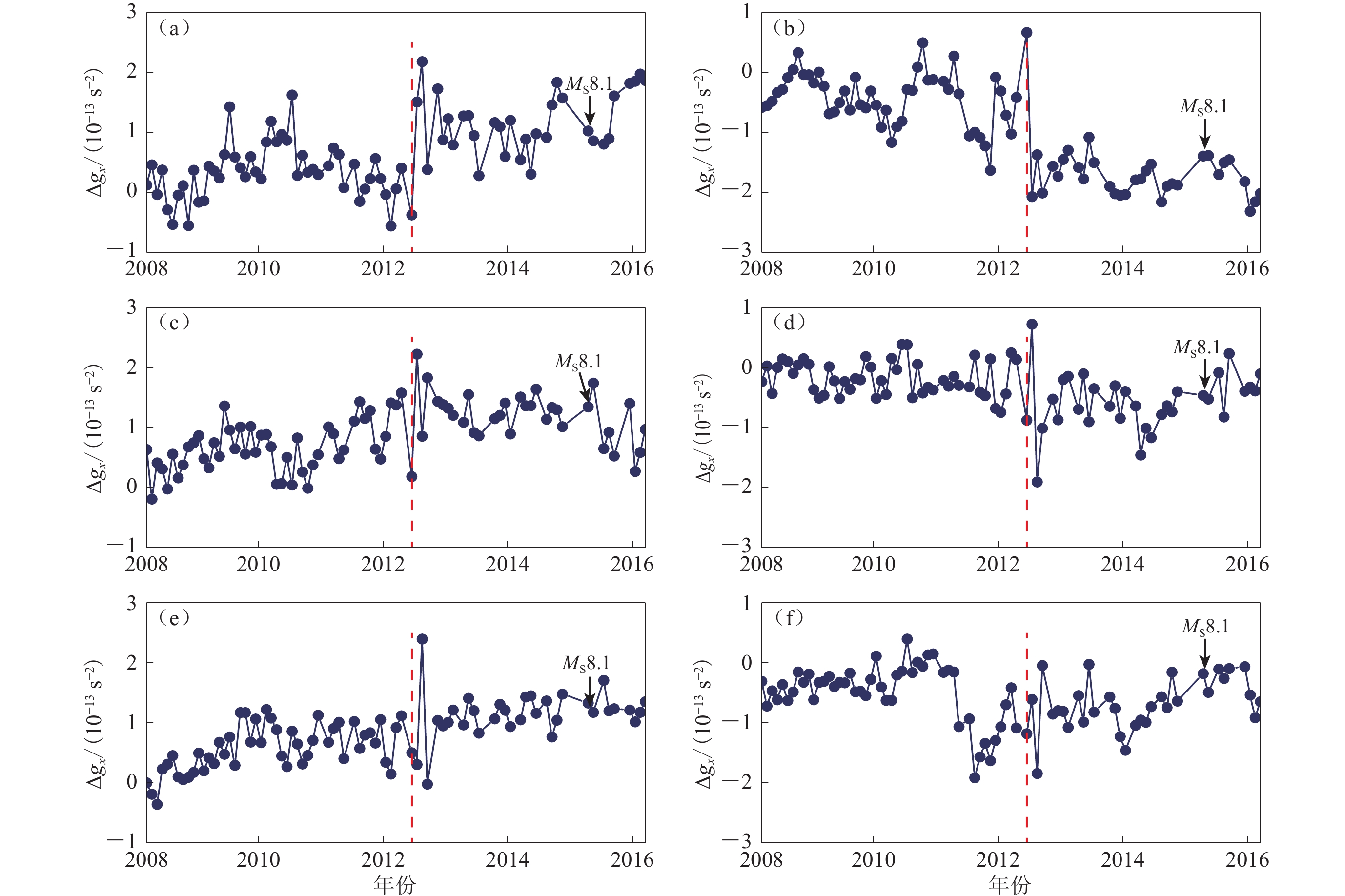
为了充分认识震中附近区域北向重力梯度随时间的变化，在研究区域内选取6个北向重力变化突出的点，即A （33.0°N，78.1°E），B （27.0°N，78.1°E），C （29.4°N，89.5°E），D （21.6°N，92.5°E），E （32.2°N，95.4°E），F （23.0°N，102.3°E），其分布如图3g所示，其中点A，C，E位于青藏地块，点B，D位于印度板块，点F位于青藏地块、华南地块与缅甸地块交界处. 以2007年1—12月的平均重力场为背景场，利用2008年1月至2016年3月筛选出的83个月的重力场模型，计算每个月的重力场模型相对背景重力场模型的偏差，采用最小二乘拟合的方法去除年和半年等周期性信号，获得特征点北向重力梯度变化的时间序列，结果如图4所示.
![]()
图 4 特征点A—F北向重力梯度变化Δgx的时间序列，红色虚线表示北向重力梯度发生跳变的时间，下同Figure 4. Time series of the northern gravity gradient changes Δgx for feature points A−F，the red dashed line denotes the time when the northern gravity gradient jumped，the same below（a） A； （b） B；（c） C；（d） D；（e） E；（f） F分析图4可知：① 由于对GRACE数据进行了300 km的扇形平滑处理，特征点位的时间序列反映了所在区域北向重力梯度的变化特征，且各点的北向重力梯度变化与该点所在处的北向重力梯度年累积变化存在较好的对应关系. 北向重力梯度在发震前后均未产生明显阶跃，但均在2012年4月发生跳变，如图4中红色虚线所示，最大变化值出现在点B （图4b），为3.74×10−13/s2，反映出尼泊尔地震前3年地下物质的调整和能量积累引起了区域物质的迁移和质量的再分布，这一变化特征与2011年日本MW9.0地震前GRACE卫星观测到的重力变化类似（邹正波等，2012）. ② 位于青藏地块的特征点A，C，E 的北向重力梯度，在2012年4月发生跳变后均比原来有所增加：2012年4月之前，点A的北向重力梯度波动比较明显，点C和E基本保持较小的变化幅度，且总体上呈平稳增加趋势；2012年4月之后，点A，C的北向重力梯度均存在不同程度的减小，点A减小的速率较大，在尼泊尔地震前先迅速增加到1.83×10−13/s2之后又迅速减小，点E的北向重力梯度在2012年4月之后基本保持不变，且在尼泊尔地震前后无明显变化. ③ 位于印度板块的B，D两点的北向重力梯度在2012年4月发生跳变后出现不同程度的减小：2012年4月之前，点B的变化幅度比较大，点D无明显变化；之后B，D两点均基本保持稳定，直至发生尼泊尔MS8.1地震. ④ 位于青藏地块、华南地块与缅甸地块交界处的点F的北向重力梯度在2012年4月跳变不是特别明显，但在2010年12月至2011年8月其北向重力梯度从0.15×10−13/s2减小至−1.91×10−13/s2，之后又快速增加，可能与缅甸2011年MS7.6地震和2012年MS7.0地震有关.
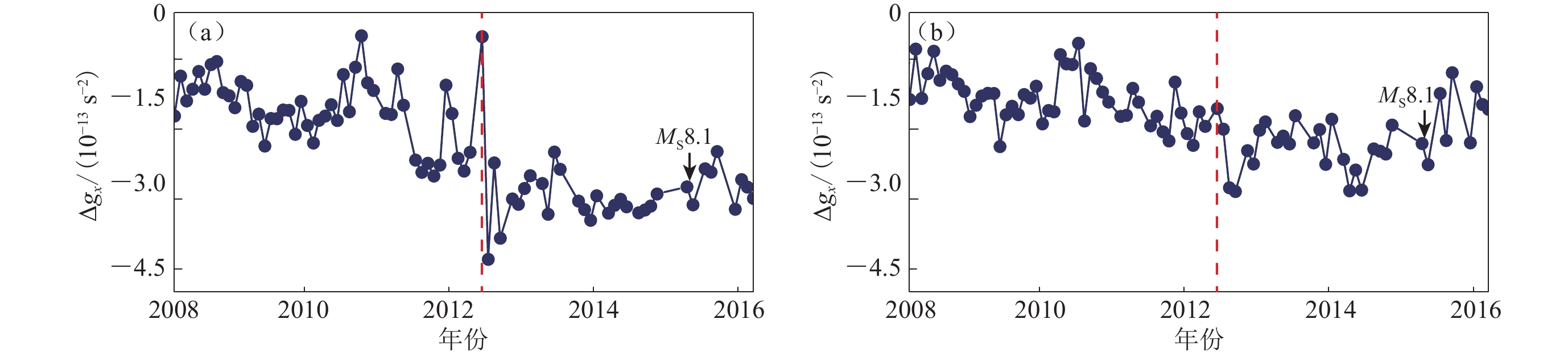
断裂带两侧的重力相对变化主要反映了构造应力作用下活动断层两盘的物质变迁和构造变形差异运动产生的重力效应（祝意青等，2009）. 为了分析断裂带的深部构造活动，采用相同的方法计算了喜马拉雅构造带两侧（印度板块相对青藏地块）北向重力梯度相对差异的时间序列，即印度板块上点B，D相对青藏地块上点C的北向重力梯度变化，结果如图5所示.
![]()
图 5 喜马拉雅断裂带两侧北向重力梯度Δgx的相对变化（a） 印度板块上点B相对于青藏地块上点C的变化； （b） 印度板块上点D相对于青藏地块上点C的变化Figure 5. The northern gravity gradient relative change Δgx series of the points in bilateral sides of Himalayan orogenic belt（a） The relative change of point B on Indian Plate to point C on Tibetan Plateau; （b） The relative change of point D on Indian Plate to point C on Tibetan Plateau由图5可知：① 从整体上看，点B，D相对点C的北向重力梯度变化趋势大致相同，印度板块上点B相对青藏地块上点C的变化幅度更大；② 具体而言，2008—2009年喜马拉雅构造带两侧北向重力梯度相对变化不明显，2009—2010年印度板块上的点B，D相对青藏地块上的点C北向重力梯度均有较小幅度的减小，2010—2011年分别增加至0.50×10−13/s2和0.34×10−13/s2，2011—2014年快速下降，最大下降幅值分别为4.80×10−13/s2和3.16×10−13/s2，2014年之后又逐渐升高，点B增加较缓慢. 总体表现出平稳变化、上升、加速下降、上升、发震的变化过程，与2008年汶川地震的变化特征相似（祝意青等，2009）.
喜马拉雅断裂带两侧北向重力梯度的相对变化过程，主要反映了断裂带构造运动引起的北向重力梯度变化.
3.3 北向重力梯度长期变化趋势
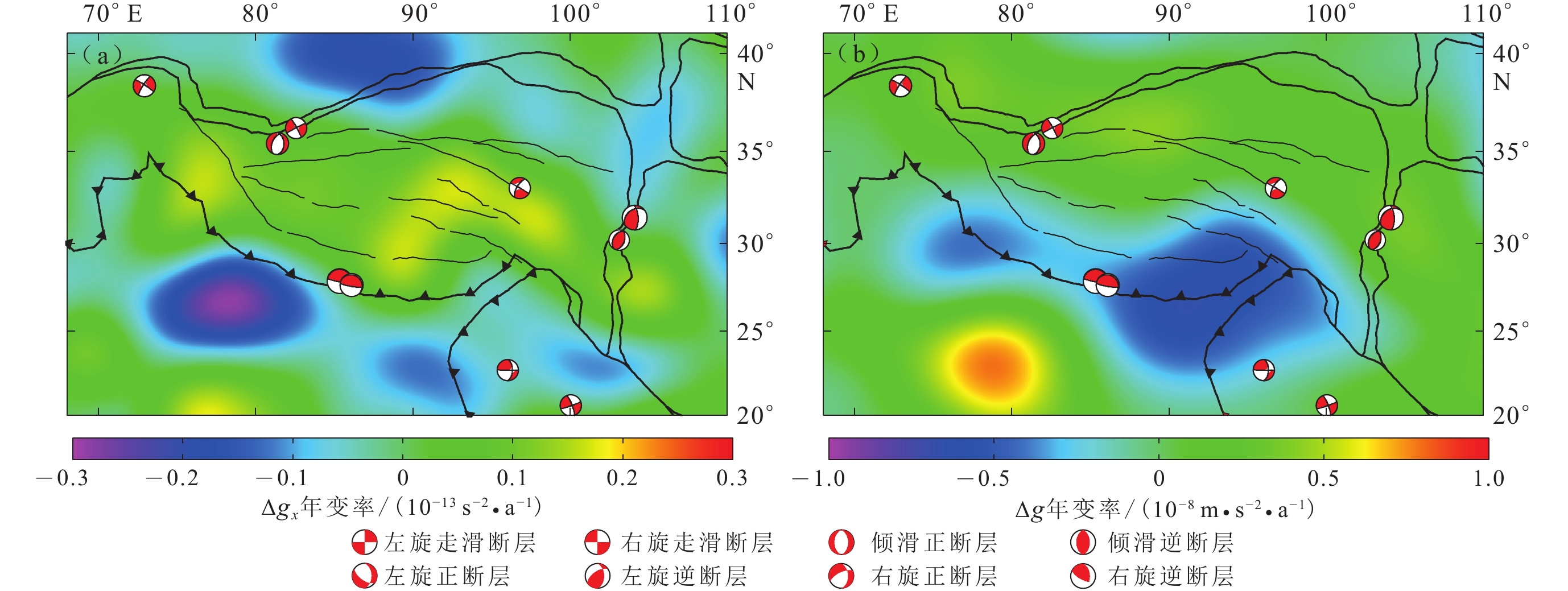
以2007年1—12月的平均重力场为背景场，将2008年1月至2014年11月筛选出的74个月的重力场与背景场进行差分，之后采用最小二乘法计算研究区0.5°×0.5°的北向重力梯度和重力年变率，结果如图6所示.
![]()
图 6 尼泊尔及其邻近区域北向重力梯度Δgx年变率（a）及重力Δg年变率（b）Figure 6. Annual change rate of northern gravity gradient Δgx （a） and gravity Δg （b） in Nepal and its vicinity areas由图6a可以看出：① 印度板块、缅甸地块以及西域地块的北向重力梯度变化均以负值为主，在印度板块北部达到最大，其年变率为−0.29×10−13/（s2·a），与印度地下水长期消耗有关（Rodell et al，2009 ）；青藏高原以及华南地块的北向重力梯度变化基本为正，青藏高原中部北向重力梯度的年变率最大，为0.18×10−13/（s2·a），其它地区北向重力梯度基本在零值附近平稳变化. ② 北向重力梯度年变率沿印度板块边界及其垂直方向在四象限正负相间分布，沿印度板块边界的东西方向年变率为负值，沿与印度板块边界垂直的南北方向年变率为正值，与2014年北向重力梯度变化的空间分布有较好的对应关系（图3g）.
重力长期变化趋势（图6b）显示：印度板块北部和喜马拉雅山东侧的负变化比较显著，分别为−0.42×10−8 m/（s2·a）和−0.66×10−8 m/（s2·a）；而在青藏地块中部和印度板块中部重力增加比较明显，重力年变率分别为0.43×10−8 m/（s2·a）和0.80×10−8 m/（s2·a）. 研究表明，喜马拉雅山东侧的重力变化可能由高山冰川消融或地壳隆升等引起（Sun et al，2009 ； Yi，Sun，2014），青藏高原湖泊众多，水含量约以1 cm/a的速率增加，导致高原中部重力的增加（Zhong et al，2009 ）.
3.4 尼泊尔MS8.1地震理论北向重力梯度同震变化
采用黏弹性分层位错模型PSGRN/PSCMP （Wang et al，2006 ）以及USGS （2015）发布的断层模型计算2015年尼泊尔MS8.1地震的同震重力变化，再利用差分法获得北向重力梯度变化（Li，Shen，2011）
$\Delta {g_x} = \frac{{g(\theta ) - g(\theta + \delta \theta )}}{{a \delta \theta }}{\text{.}}$
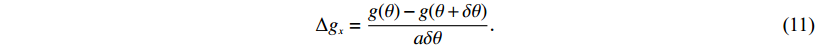
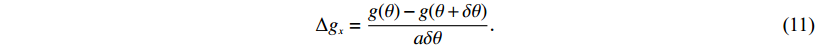
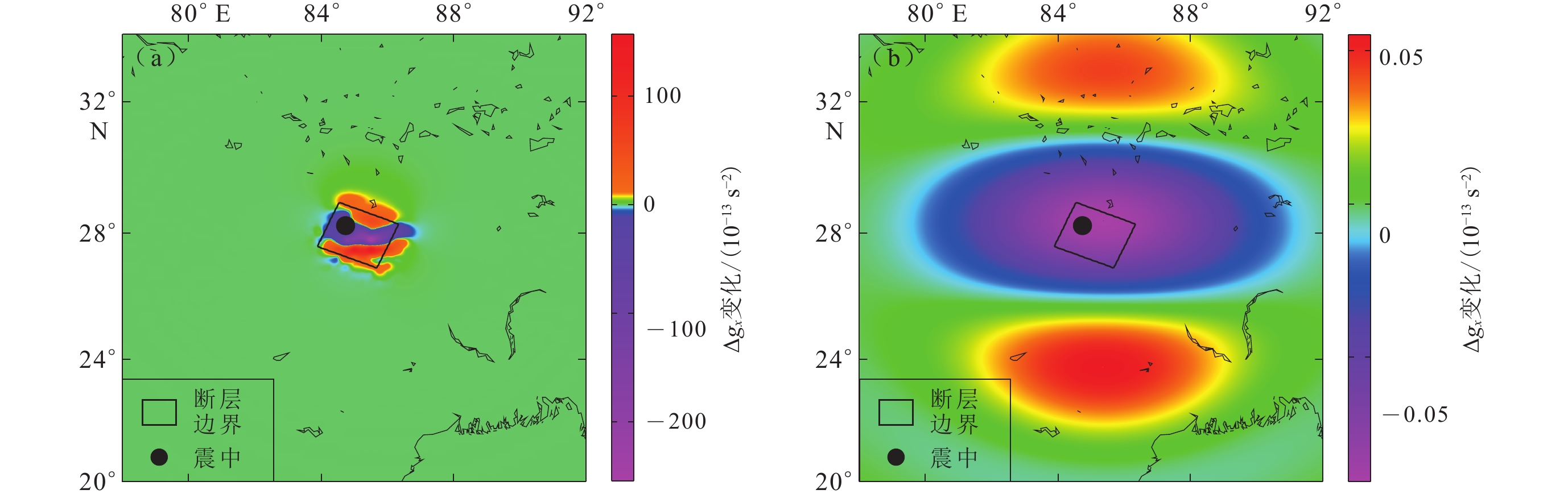
(11) 计算过程中采用4层地球模型（表1），各参数均取自Crust1.0. 为了与GRACE卫星的空间观测结果保持一致，需要在位错模型计算结果的基础上加入地表垂直形变引起的空间改正（Sun et al，2009 ），结果如图7a所示. 将改正后的北向重力梯度同震变化进行球谐系数展开并截断至60阶，然后采用300 km扇形滤波，以达到与GRACE一致的空间分辨率，结果如图7b所示.
![]()
图 7 尼泊尔MS8.1地震的理论北向重力梯度Δgx同震变化（a） 空间固定点的北向重力梯度变化； （b） 平滑处理后的北向重力梯度变化Figure 7. Theoretically coseismic northern gravity gradient Δgx change of the Nepal MS8.1 earthquake calculated by PSGRN/PSCMP（a） Northern gravity gradient change on the space-fixed points; （b） Northern gravity gradient change after filtering由图7可知，理论模拟得到的北向重力梯度呈“正—负—正”的空间分布特征，经过空间平滑后，可体现较大尺度的特征，北向重力梯度由−244×10−13/s2—152×10−13/s2减少至−0.09×10−13/s2—0.06×10−13/s2，变化幅度下降较大，同时空间范围也发生很大变化.
利用地震前、后各3个月的平均重力场的差分和全球陆地数据同化系统（global land data assimilation system，简写为GLDAS）1°×1°产品，并充分考虑土壤水含量和雪水变化的影响，将格网数据展开为球谐系数并截断至60阶，采用与GRACE数据相同的处理方法，将土壤水和雪水变化引起的北向重力梯度变化从GRACE观测值中扣除，所得的北向重力梯度比理论模拟结果高一个量级，未提取出北向重力梯度“正—负—正”的空间分布特征.
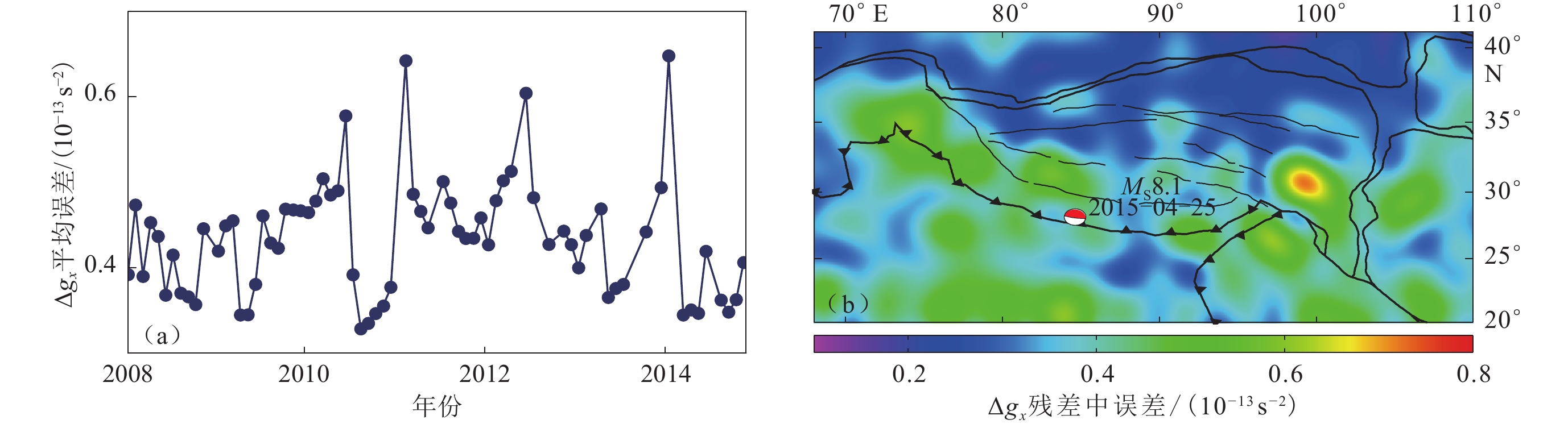
表 1 尼泊尔MS8.1地震的4层地球模型Table 1. The four layer model of Nepal MS8.1 earthquake from Crust1.0深度/km 密度/(103 kg·m−3) vP/(km·s−1) vS/(km·s−1) 0—23.65 2.72 6.00 3.52 23.65—36.73 2.79 6.30 3.68 36.73—50.90 2.85 6.60 3.82 50.90—∞ 3.45 8.44 4.68 GRACE在发布月重力场模型的同时，也发布了对应阶次球谐系数的标定误差，利用标定误差，基于误差传播定律，可以得到相应月份北向重力梯度误差的全球分布（Wahr et al，2006 ）. 将研究区域所有格网点的平均值作为北向重力梯度平均误差的估计值，得到尼泊尔及其邻近区域2008年1月—2014年11月北向重力梯度平均误差的时间序列，结果如图8a所示，其中2010年6月、2011年2月、2012年6月和2014年1月的平均误差较大，分别为0.58×10−13/s2，0.64×10−13/s2，0.60×10−13/s2，0.65×10−13/s2，其余月份的平均误差均介于0.33×10−13—0.51×10−13/s2之间，2008—2014年北向重力梯度的平均误差均值为0.43×10−13/s2，将该值作为尼泊尔及其邻近区域北向重力梯度误差的估值之一.
![]()
图 8 尼泊尔及其邻近区域北向重力梯度Δgx误差（a） 2008—2014 Δgx年平均误差时间序列；（b） 拟合所得北向重力梯度残差中误差的空间分布Figure 8. Errors of northern gravity gradient Δgx in Nepal and its vicinity areas（a） The regional average errors change series from 2008 to 2014; （b） The root mean square errors of the northern gravity gradient residuals by using least squares fitting此外，在对研究区域北向重力梯度年变率进行拟合的同时，也得到了每个格网点的残差，残差的中误差可作为误差的估计（Wahr et al，2004 ）. 研究区域北向重力梯度残差中误差的空间分布如图8b所示，其变化幅值为0.17×10−13—0.72×10−13/s2，将所有格网点残差中误差的平均值作为研究区域北向重力梯度的误差，其值为0.38×10−13/s2. Wahr等（2004）指出，拟合法所得的误差对时间序列本身的幅度有减弱作用，需要乘以一个大于1的尺度因子，并基于模拟实验得出该尺度因子约为1.1，依据该尺度因子，将拟合法所得的尼泊尔及其邻近区域北向重力梯度误差调整为0.42×10−13/s2. 利用拟合法所得研究区域的误差与利用模型标定误差计算的误差较为一致，综合考虑标定误差和拟合误差，在300 km扇形平滑的空间分辨率下，尼泊尔及其邻近区域北向重力梯度的误差约为0.43×10−13/s2.
PSGRN/PSCMP模拟得到的北向重力梯度同震变化范围为−0.09×10−13—0.06×10−13/s2，变化幅度较小，模拟值比GRACE北向重力梯度的精度低，说明尼泊尔MS8.1地震北向重力梯度的同震变化在GRACE卫星的检测范围之外，以现有的GRACE卫星的观测精度提取该地震北向重力梯度的同震变化是较难实现的.
地震引起的同震重力变化还与发震模式有关，Sun和Okubo （2004）的研究结果表明，张裂型地震产生的重力变化远大于同一震级的剪切型地震，MW≥9.0剪切型或MW≥7.5张裂型地震产生的同震重力变化均可被GRACE观测到. 尼泊尔MS8.1地震属于低角度逆冲型地震（Yagi，Okuwaki，2015；杨晓平等，2016），北向重力梯度同震效应的理论值变化幅度较小，可能与该地震的发震模式有关.
4. 讨论与结论
本文以2015年9月GRACE月重力场模型为例说明了北向重力梯度对“南北条带”误差的压制作用，采用300 km扇形滤波，分析了尼泊尔MS8.1地震北向重力梯度的时空变化特征，避免了去相关滤波对真实信号的削弱，研究结果表明：
1） 尼泊尔MS8.1地震发生在北向重力梯度正负变化的零值线附近，与地面流动重力及GRACE卫星重力观测结果一致.
2） 在尼泊尔MS8.1地震震中附近选取6个特征点，各点的北向重力梯度在发震前后未产生明显阶跃，但均在2012年4月发生跳变，最大幅值可达3.74×10−13/s2，反映了尼泊尔地震前的物质运动和能量积累；喜马拉雅构造带两侧的北向重力梯度相对变化表现为平稳变化、上升、加速下降、上升、发震的过程，这一特征与汶川地震较为类似.
3） 北向重力梯度年变率沿印度板块边界及其垂直方向在四象限正负相间分布，沿印度板块边界的东西方向年变率为负值，沿与印度板块边界垂直的南北方向年变率为正值.
4） 在300 km扇形平滑的空间分辨率下，PSGRN/PSCMP模型计算的空间固定点的北向重力梯度同震变化范围为−0.09×10−13—0.06×10−13/s2，并且呈“正—负—正”的空间分布特征；由GRACE数据所得的尼泊尔及其邻近区域北向重力梯度的误差约为0.43×10−13/s2，说明尼泊尔MS8.1地震的同震效应淹没在GRACE观测到的其它信号中，利用GRACE数据提取尼泊尔地震北向重力梯度的同震变化是比较困难的.
上海天文台李进副研究员在位错模型学习上给予了帮助和指导，审稿专家对本文提出了宝贵的意见，作者在此一并表示感谢.
-
![]()
图 1 天津某地活断层浅层地震勘探数据的时间序列
Figure 1. Time series of shallow seismic survey implemented in Tianjin
![]()
图 2 图1所示时间序列在频率-波数域中的能量分布（a）及剔除体波后的面波能量（b）
Figure 2. Energy distribution in frequency-wave number domain of the time series shown in Fig.1 （a） and surface wave energy after removing the body waves （b）
![]()
图 3 频率-相速度域中面波能量分布及提取的多阶振型频散曲线
Figure 3. Dispersion curves and energy distribution of surface waves in frequency-phase velocity domain
![]()
图 4 只考虑基阶振型的S波反演结果
（a） 初始模型经30次迭代收敛至最终反演模型；（b） 观测基阶振型与反演模型的频散曲线拟合
Figure 4. The inversed results considering only the fundamental mode
（a） The process of the initial model converged to the final model after 30 iterations；（b） The fitting of the dispersions of observed one and inversed model
![]()
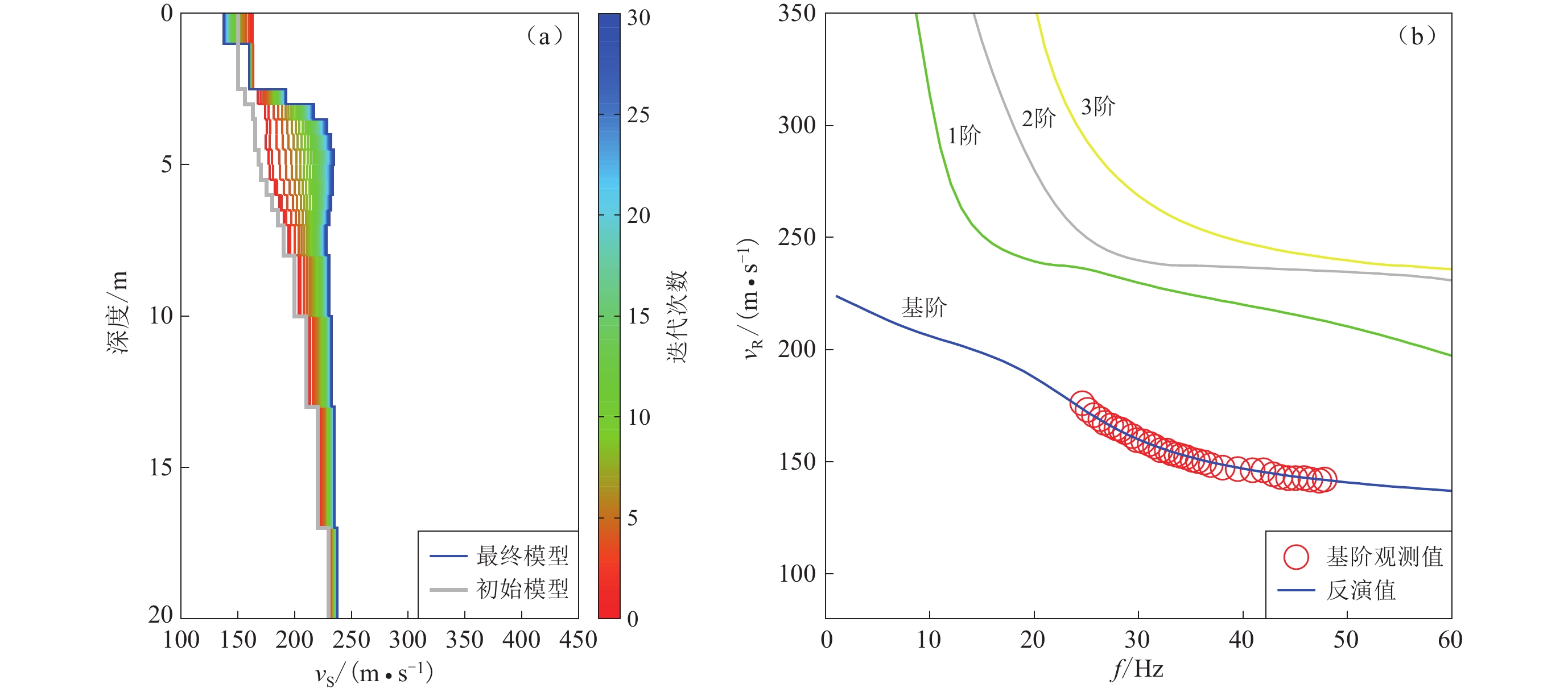
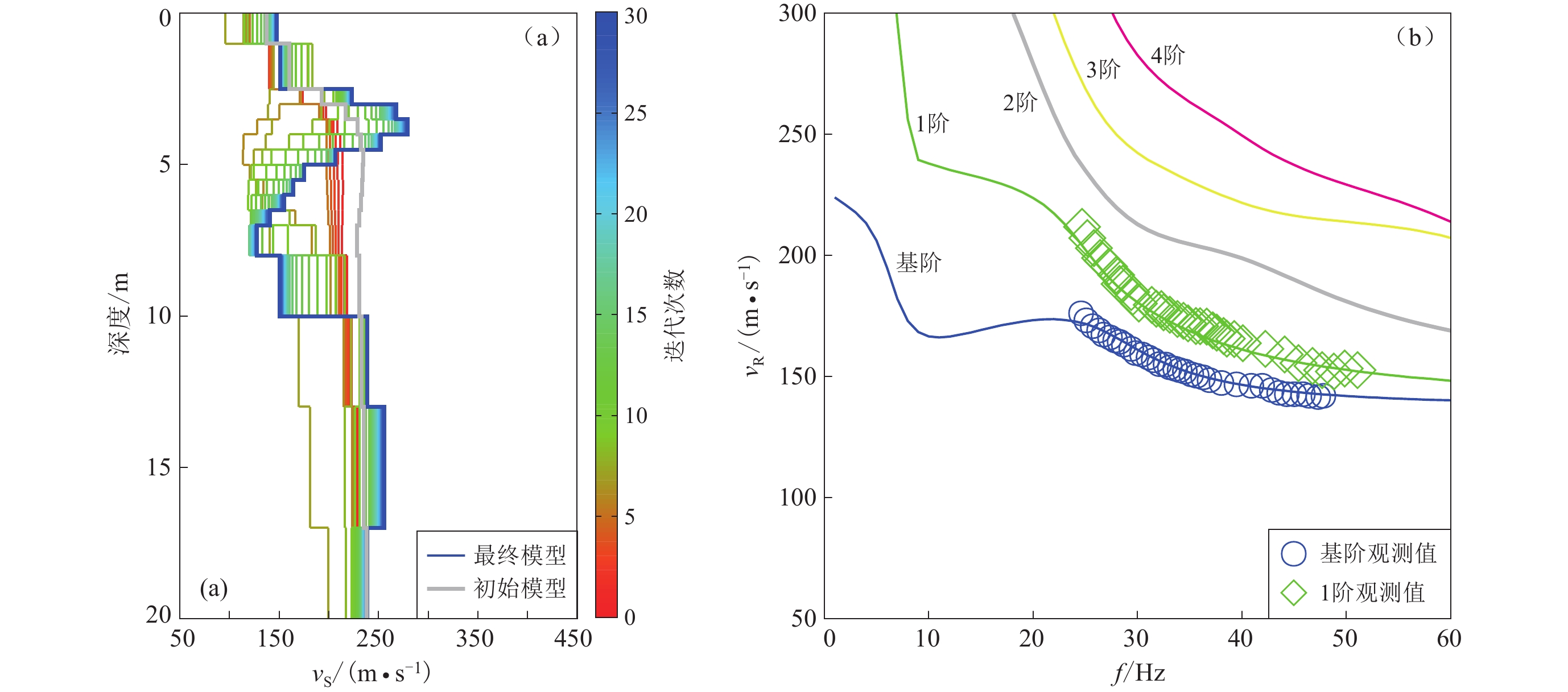
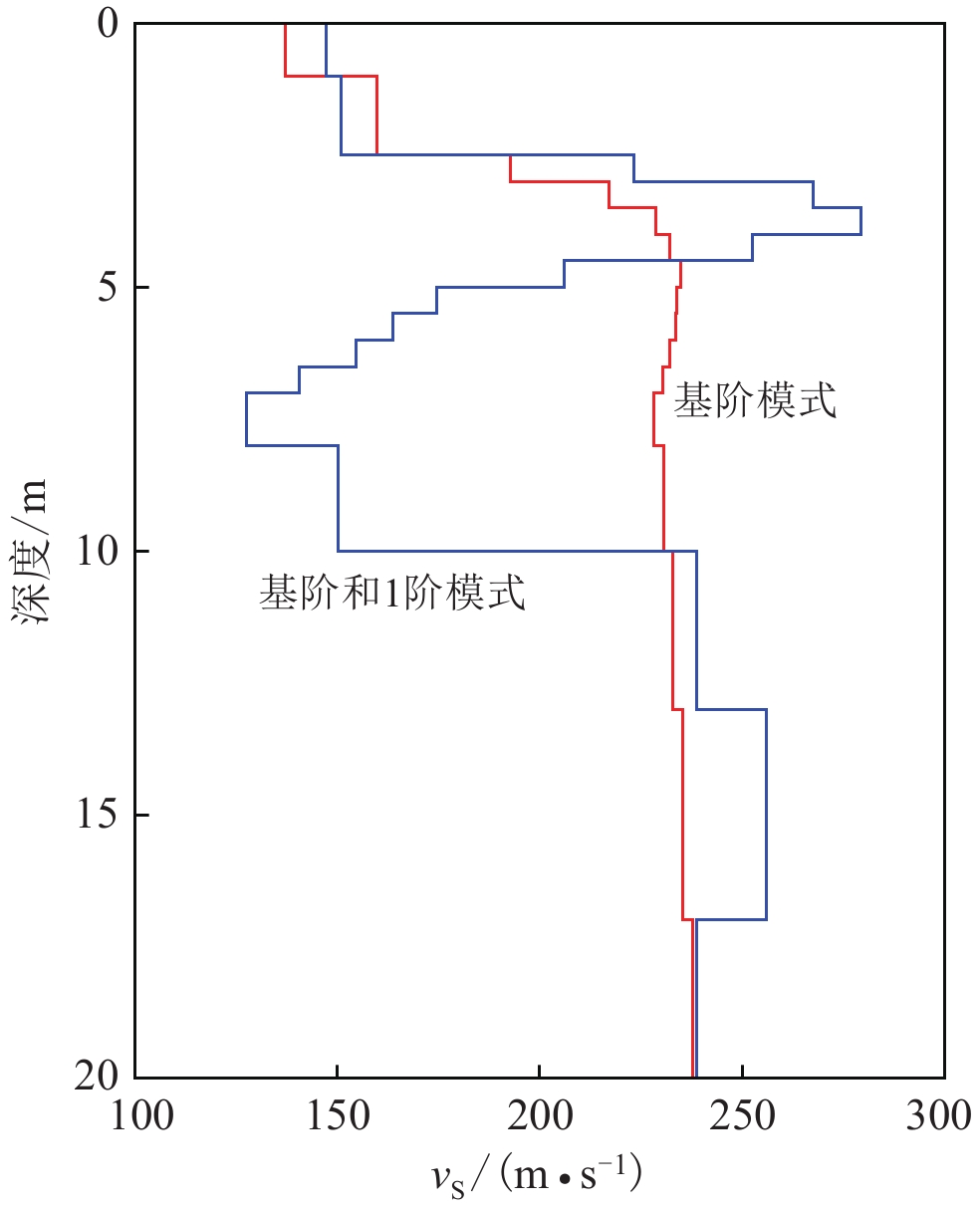
图 5 同时考虑基阶和1阶高振型下S波的反演结果
（a） 由初始模型经30次迭代收敛至最终反演模型；（b） 观测的基阶振型与反演模型的频散曲线拟合
Figure 5. The inversion results considering the fundamental and first-mode Rayleigh waves
（a） The process of the initial model converged to the final model after 30 iterations; （b） The fitting of the dispersions of observed one and inversed model
![]()
图 6 仅考虑基阶与考虑基阶和1阶振型的反演结果的对比
Figure 6. Comparison ofinversion result by considering fundamental wave with that by fundamental and the first-mode waves
表 1 初始模型参数和反演结果
Table 1 The parameters of the final and initial model
层数 层厚/m ρ/（g·cm−3） vP/（m·s−1） 初始vS/（m·s−1） 反演vS/（m·s−1） 1 1.0 1.60 300 150 137.2 2 1.5 1.66 350 150 159.9 3 0.5 1.73 400 156 192.7 4 0.5 1.77 450 163 217.0 5 0.5 1.79 500 165 228.8 6 0.5 1.79 550 165 232.2 7 0.5 1.78 560 168 234.7 8 0.5 1.78 570 170 233.7 9 0.5 1.79 580 175 233.5 10 0.5 1.79 590 180 232.1 11 0.5 1.79 600 185 230.3 12 1.0 1.79 700 190 228.1 13 2.0 1.79 800 200 230.7 14 3.0 1.79 900 210 232.9 15 4.0 1.80 1 100 220 235.3 半空间 1.80 1 200 230 237.7 
下载: 导出CSV
-
陈文超, 王伟, 高静怀, 姜呈馥, 雷江莉. 2013. 基于地震信号波形形态差异的面波噪声稀疏优化分离方法[J]. 地球物理学报, 56（8）: 2771-2782. Chen W C, Wang W, Gao J H, Jiang C F, Lei J L. 2013. Sparsity optimized separation of Ground-roll noise based on morphological diversity of seismic waveform components[J]. Chinese Journal of Geophysics, 56（8）: 2771-2782（in Chinese）.
方盛明, 张先康, 刘保金, 徐锡伟, 白登海, 姬继法. 2002. 探测大城市活断层的地球物理方法[J]. 地震地质, 24（4）: 606-613. Fang S M, Zhang X K, Liu B J, Xu X W, Bai D H, Ji J F. 2002. Geophysical methods for the exploration of urban active faults[J]. Seismology and Geology, 24（4）: 606-613（in Chinese）.
关小平, 黄嘉正, 周鸿秋. 1993. 工程勘察中稳态瑞利面波法解释理论的探讨[J]. 地球物理学报, 36（1）: 96-105. Guan X P, Huang J Z, Zhou H Q. 1993. Probe the interpretation theory of steady-state Rayleigh wave method in engineering exploration[J]. Chinese Journal of Geophysics, 36（1）: 96-105（in Chinese）.
刘庆华, 鲁来玉, 王凯明. 2015. 主动源和被动源面波浅勘方法综述[J]. 地球物理学进展, 30（6）: 2906-2922. Liu Q H, Lu L Y, Wang K M. 2015. Review on the active and passive surface wave exploration method for the near-surface structure[J]. Progress in Geophysics, 30（6）: 2906-2922（in Chinese）.
刘云祯, 王振东. 1996. 瞬态面波法的数据采集处理系统及其应用实例[J]. 物探与化探, 20（1）: 28-34. Liu Y Z, Wang Z D. 1996. Data collection and processing system of transient surface wave method and examples of its application[J]. Geophysical and Geochemical Exploration, 20（1）: 28-34（in Chinese）.
鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究[J]. 地球物理学报, 49（4）: 1082-1091. Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes[J]. Chinese Journal of Geophysics, 49（4）: 1082-1091（in Chinese）.
罗银河, 夏江海, 刘江平, 刘庆生. 2008. 基阶与高阶瑞利波联合反演研究[J]. 地球物理学报, 51（1）: 242-249. Luo Y H, Xia J H, Liu J P, Liu Q S. 2008. Joint inversion of fundamental and higher mode Rayleigh waves[J]. Chinese Journal of Geophysics, 51（1）: 242-249（in Chinese）.
王辉, 丁志峰. 2006. 浅层地震勘探资料处理中的速度分析参数选取[J]. 地震地质, 28（4）: 597-603. Wang H, Ding Z F. 2006. Parameters selection for velocity analysis in shallow seismic data processing[J]. Seismology and Geology, 28（4）: 597-603（in Chinese）.
夏江海, 高玲利, 潘雨迪, 沈超, 尹晓菲. 2015. 高频面波方法的若干新进展[J]. 地球物理学报, 58（8）: 2591-2605. Xia J H, Gao L L, Pan Y D, Shen C, Yin X F. 2015. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 58（8）: 2591-2605（in Chinese）.
杨成林. 1989. 瑞雷波法勘探原理及其应用[J]. 物探与化探, 13（6）: 465-468. Yang C L. 1989. The principle and application of Rayleigh wave exploration method[J]. Geophysical and Geochemical Exploration, 13（6）: 465-468（in Chinese）.
张碧星, 鲁来玉, 鲍光淑. 2002. 瑞利波勘探中" 之”字形频散曲线研究[J]. 地球物理学报, 45（2）: 263-274. Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese Journal of Geophysics, 45（2）: 263-274（in Chinese）.
Al-Hunaidi M O. 1992. Difficulties with phase spectrum unwrapping in spectral analysis of surface waves nondestructive testing of pavements[J]. Can Geotech J, 29（3）: 506-511.
Alleyne D, Cawley P. 1990. A two-dimensional Fourier transform method for the measurement of propagating multimode signals[J]. J Acoust Soc Am, 89（3）: 1159-1168.
Forchap E A, Schmid G. 1998. Experimental determination of Rayleigh-wave mode velocities using the method of wave number analysis[J]. Soil Dyn Earthq Eng, 17（3）: 177-183.
Gabriels P, Snieder R, Nolet G. 1987. In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves[J]. Geophys Prospect, 35（2）: 187-196.
Lu L Y, Zhang B X. 2004. Analysis of dispersion curves of Rayleigh waves in the frequency-wavenumber domain[J]. Can Geotech J, 41（4）: 583-598.
Lu L Y, Wang C H, Zhang B X. 2007. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer: numerical and laboratory study[J]. Geophys J Int, 168（3）: 1235-1246.
McMechan G A, Yedlin M J. 1981. Analysis of dispersive waves by wave field transformation[J]. Geophysics, 46（6）: 869-874.
Nazarian S, Stokoe II K H. 1986. In Situ Determination of Elastic Moduli of Pavement Systems by Spectral-Analysis-of-Surface-Waves Method （practical aspects）[R]. Austin: Center for Transportation Research, the University of Texas at Austin: 1123-1.
Park C B, Miller R D, Xia J J. 1999. Multichannel analysis of surface waves[J]. Geophysics, 64（3）: 800-808.
Socco L V, Foti S, Boiero D. 2010. Surface-wave analysis for building near-surface velocity models-established approaches and new perspectives[J]. Geophysics, 75（5）: 75A83-75A102.
Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh wave[J]. Geophysics, 64（3）: 691-700.
-
期刊类型引用(48)
1. Yu Li，Yuebing Wang，Lijiang Zhao，Hongbo Shi，Pingping Wang. Kinematic deformation and intensity assessment of the 2021 Maduo M_S7.4 earthquake in Qinghai revealed by high-frequency GNSS. Geodesy and Geodynamics. 2024(03): 230-240 . 
必应学术
2. 宫悦，龙锋，赵敏，杨鹏，王宇玺，梁明剑，乔慧珍，王宇航. 2022年6月10日四川马尔康M_S6.0震群序列时空演化特征. 地震学报. 2024(02): 173-191 . 本站查看
3. 杨晨艺，石富强，季灵运，杨宜海，苏利娜，杨敏，郑怡. 2013年岷县漳县M_S6.6地震和2017年九寨沟M_S7.0地震震前地球物理观测异常空间分布机理分析. 地震学报. 2024(02): 307-326 . 本站查看
4. 王莹，金昭娣，赵韬. 2022年四川马尔康6.0级震群序列震源机制特征分析. 地震研究. 2024(03): 379-390 . 百度学术
5. 朱家正，孙玉军，谢志远，吴刚. 四川大岗山水库蓄水对2022年泸定M_S6.8地震及余震的影响. 地质力学学报. 2024(02): 363-376 . 百度学术
6. 冯锐. 魏晋·说说地震活动性——漫步地震五千年(7). 地震科学进展. 2024(05): 359-371 . 百度学术
7. 郑文俊，彭慧，刘兴旺，张竹琪，张冬丽，魏拾其，王旭龙. 鄂尔多斯活动地块边界带15000年以来强震活动与现今大地震空区. 科学通报. 2024(18): 2632-2647 . 百度学术
8. 李兵，郭啟良，姜大伟，丁立丰，王建新，许俊闪，王显军. 汶川和芦山地震前后浅部应力对深部应力的响应及地震危险性分析. 地质学报. 2023(02): 339-348 . 百度学术
9. 宋程，张永仙，周少辉，毕金孟，徐小远. 2021年玛多M_S7.4地震的PI热点特征回溯性预测研究. 地震研究. 2023(02): 226-236 . 百度学术
10. 梁明剑，周文英，董云，廖程，左洪，陈翰，赵国华. 巴颜喀拉块体内部NW向主要断裂研究新进展. 四川地震. 2023(01): 12-17 . 百度学术
11. 董金元，周晓成，李营，李静超. 2021年青海玛多M_W7.4地震地表破裂带CO_2脱气特征. 第四纪研究. 2023(02): 485-493 . 百度学术
12. 王博，崔凤珍，刘静，周永胜，徐胜，邵延秀. 玛多M_S7.4地震断层土壤气特征与地表破裂的相关性. 地震地质. 2023(03): 772-794 . 百度学术
13. 张致伟，龙锋，石富强，路茜，杨宜海，杨星，王迪，祁玉萍，杨鹏. 2022年6月1日四川芦山M_S6.1地震的发震构造与力学机制探讨. 地球物理学报. 2023(10): 4095-4110 . 百度学术
14. 黄伟亮，张家乐，项闻，杨虔灏. 晚第四纪以来巴塘断裂的活动特征及滑动速率. 地震地质. 2023(06): 1265-1285 . 百度学术
15. 王阅兵，李瑜，蔡毅，蒋连江，师宏波，江在森，甘卫军. GNSS观测的2021年5月22日玛多M_S7.4地震同震位移及其约束反演的滑动破裂分布. 地球物理学报. 2022(02): 523-536 . 百度学术
16. 梁明剑，黄飞鹏，孙凯，张会平，吴微微，张佳伟，杜方，周文英. 巴颜喀拉块体内部五道梁-长沙贡玛断裂中段全新世活动及最新古地震证据. 地球科学. 2022(03): 766-778 . 百度学术
17. Jihong LIU，Jun HU，Zhiwei LI，Zhangfeng MA，Lixin WU，Weiping JIANG，Guangcai FENG，Jianjun ZHU. Complete three-dimensional coseismic displacements due to the2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Science China(Earth Sciences). 2022(04): 687-697 . 必应学术
18. Jihong LIU，Jun HU，Zhiwei LI，Zhangfeng MA，Lixin WU，Weiping JIANG，Guangcai FENG，Jianjun ZHU. Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Science China(Life Sciences). 2022(04): 687-697 . 必应学术
19. 刘计洪，胡俊，李志伟，马张烽，吴立新，姜卫平，冯光财，朱建军. 融合哨兵1号和ALOS-2数据的2021年青海玛多地震高精度三维同震形变场研究. 中国科学:地球科学. 2022(05): 882-892 . 百度学术
20. 姚文倩，王子君，刘静，刘小利，韩龙飞，邵延秀，王文鑫，徐晶，秦可心，高云鹏，王焱，李金阳，曾宪阳. 2021年青海玛多M_W7.4地震同震地表破裂长度的讨论. 地震地质. 2022(02): 541-559 . 百度学术
21. 刘小利，夏涛，刘静，姚文倩，徐晶，邓德贝尔，韩龙飞，贾治革，邵延秀，王焱，乐子扬，高天琪. 2021年青海玛多M_W7.4地震分布式同震地表裂缝特征. 地震地质. 2022(02): 461-483 . 百度学术
22. 李兵，谢富仁，黄金水，徐锡伟，郭啟良，张广伟，许俊闪，王建新，姜大伟，王健，丁立丰. 龙门山断裂带大邑地震空区地应力状态与地震危险性. 中国科学:地球科学. 2022(07): 1409-1418 . 百度学术
23. Bing LI，Furen XIE，Jinshui HUANG，Xiwei XU，Qiliang GUO，Guangwei ZHANG，Junshan XU，Jianxin WANG，Dawei JIANG，Jian WANG，Lifeng DING. In situ stress state and seismic hazard in the Dayi seismic gap of the Longmenshan thrust belt. Science China(Earth Sciences). 2022(07): 1388-1398 . 必应学术
24. Guanghao Ha，Jinrui Liu，Zhikun Ren，Xiaoxiao Zhu，Guodong Bao，Dengyun Wu，Zhiliang Zhang. The Interpretation of Seismogenic Fault of the Maduo Mw 7.3Earthquake, Qinghai Based on Remote Sensing Images——A Branch of the East Kunlun Fault System. Journal of Earth Science. 2022(04): 857-868 . 必应学术
25. 韩明明，陈立春，曾蒂，李彦宝，梁明剑，高帅坡，王冬兵，罗亮. 鲜水河断裂带色拉哈段中谷村一带的最新地表破裂讨论. 地质力学学报. 2022(06): 969-980 . 百度学术
26. 杜航，杨云，郑江蓉，王俊，张扬，宫杰. 青海玛多M_S7.4地震前b值时空变化特征. 震灾防御技术. 2022(04): 691-700 . 百度学术
27. 李昭，付碧宏. 东昆仑断裂带玛沁—玛曲段晚第四纪构造活动特征的地貌响应定量研究. 地震地质. 2022(06): 1421-1447 . 百度学术
28. Ruifang Yu，Xiao Hu，Ruizhi Wen. Preface to the special issue on ground motion input at dam sites and reservoir earthquakes. Earthquake Science. 2022(05): 311-313 . 必应学术
29. 姜佳佳，冯建刚. 2017年九寨沟7.0级地震前应力状态及b值异常特征研究. 地震工程学报. 2021(03): 575-582 . 百度学术
30. 潘家伟，白明坤，李超，刘富财，李海兵，刘栋梁，Marie-Luce CHEVALIER，吴坤罡，王平，卢海建，陈鹏，李春锐. 2021年5月22日青海玛多M_S7.4地震地表破裂带及发震构造. 地质学报. 2021(06): 1655-1670 . 百度学术
31. 詹艳，梁明剑，孙翔宇，黄飞鹏，赵凌强，宫悦，韩静，李陈侠，张培震，张会平. 2021年5月22日青海玛多M_S7.4地震深部环境及发震构造模式. 地球物理学报. 2021(07): 2232-2252 . 百度学术
32. 李智敏，李文巧，李涛，徐岳仁，苏鹏，郭鹏，孙浩越，哈广浩，陈桂华，袁兆德，李忠武，李鑫，杨理臣，马震，姚生海，熊仁伟，张彦博，盖海龙，殷翔，徐玮阳，董金元. 2021年5月22日青海玛多M_S7.4地震的发震构造和地表破裂初步调查. 地震地质. 2021(03): 722-737 . 百度学术
33. 徐志国，梁姗姗，张广伟，梁建宏，邹立晔，李旭茂，陈彦含. 2021年5月22日青海玛多M_S7.4地震发震构造分析. 地球物理学报. 2021(08): 2657-2670 . 百度学术
34. 赵韬，王莹，马冀，邵若潼，徐一斐，胡景. 2021年青海玛多7.4级地震序列重定位和震源机制特征. 地震地质. 2021(04): 790-805 . 百度学术
35. 任晴晴，陆丽娜，钱小仕，赵宜宾. 巴颜喀拉地块及其周边地震危险性分析. 地震. 2021(03): 144-156 . 百度学术
36. 张志文，任俊杰，章小龙. 高精度无人机航测在2021年玛多7.4级地震地表破裂精细研究中的应用. 震灾防御技术. 2021(03): 437-447 . 百度学术
37. 盖海龙，姚生海，杨丽萍，亢太波，殷翔，陈庭，李鑫. 青海玛多“5·22”M_S7.4级地震的同震地表破裂特征、成因及意义. 地质力学学报. 2021(06): 899-912 . 百度学术
38. 姚生海，盖海龙，殷翔，李鑫. 青海玛多M_S7.4地震地表破裂带的基本特征和典型现象. 地震地质. 2021(05): 1060-1072 . 百度学术
39. 尹晓菲，张国民，邵志刚，王芃，孙鑫喆. 华北地区强震活动特点研究. 地震. 2020(01): 11-33 . 百度学术
40. 胡翔，白文科，董鑫. 四川省九寨沟县地震前后区域生态环境质量评价. 生态学杂志. 2020(03): 969-978 . 百度学术
41. 付平，张新辉，尹健民，韩晓玉，周春华. 龙门山断裂带中段及邻区构造变形特征及应力场演化的数值模拟研究. 地震研究. 2020(01): 28-36+207 . 百度学术
42. 万森林，张军龙，刘明军，贺为民，李海龙，郭长宝，李智敏. 岷山断块的发震构造与地震活动性分析. 地震. 2020(02): 49-70 . 百度学术
43. 张翼，唐姝娅，周妍，陈文捷. 四川地震应急指挥大厅综合调度平台设计与实现. 地震科学进展. 2020(01): 27-35 . 百度学术
44. 邵志刚，冯蔚，王芃，尹晓菲. 中国大陆活动地块边界带的地震活动特征研究综述. 地震地质. 2020(02): 271-282 . 百度学术
45. 徐旭，徐锦承，张伟. 2017年四川九寨沟M_s7.0地震及余震定位研究. 中国地震. 2020(02): 324-332 . 百度学术
46. 李莎，阎春恒，周斌，郭培兰，周军学. 2016年广西苍梧M_S5.4地震前地震活动图像演化特征. 华北地震科学. 2020(03): 19-26 . 百度学术
47. 唐小明，王晓琴，贺维，吴世磊，苏宇，陈涤非，鄢武先，邓东周. 九寨沟地震灾区珍稀保护动物受损栖息地维管植物区系组成及特征分析. 四川林业科技. 2020(06): 124-130 . 百度学术
48. Feng Long，GuiXi Yi，SiWei Wang，YuPing Qi，Min Zhao. Geometry and tectonic deformation of the seismogenic structure for the 8 August 2017 M_S 7.0 Jiuzhaigou earthquake sequence, northern Sichuan, China. Earth and Planetary Physics. 2019(03): 253-267 . 必应学术
其他类型引用(19)
计量
- 文章访问数: 1529
- HTML全文浏览量: 904
- PDF下载量: 65
- 被引次数: 67
