A geomagnetic variation prediction method based on chaotic VMD-LSTM neural network
-
摘要:
针对地磁变化场的非平稳性、非线性以及物理模型难以预测的特点,提出了一种改进的长短期记忆网络预测方法并进行了验证。首先应用变分模态分解方法对地磁台站数据进行去噪,再根据地磁变化的混沌特性引入混沌理论对样本集进行优化,最终以长短期记忆网络预测地磁变化并对改进前后的方法进行了对比。结果显示,优化方法的预测效果较稳定,平均绝对误差小于2 nT,相关指数R2超过0.8,预测值与实测值的拟合度较高,有效预测时长可达2.5天,且在中国大陆的泛用性较好。
Abstract:In view of the nonstationarity and nonlinearity of geomagnetic variation field and the difficulty of physical model prediction, an improved LSTM (long short-term memory) neural network prediction method is proposed and verified by tests. Firstly, the variational mode decomposition (VMD) method is used to denoise the geomagnetic data, and then the chaos theory is introduced to optimize the sample set according to the chaotic characteristics of geomagnetic variation. Finally, the LSTM network is used to predict geomagnetic variation. The results show that the prediction of the optimized method is relatively stable, mean absolute error is less than 2 nT, correlative coefficient R2 is larger than 0.8, the predicted value is well consistent with the measured value, and the effective prediction time can reach 2.5 days, and it has good universality in Chinese Mainland.
-
Keywords:
- variational mode decomposition /
- chaos theory /
- LSTM /
- geomagnetic variation
-
引言
地球磁场是地球固有的物理性质,地球磁场随时间的短期变化称地球变化磁场或地磁变化场(徐文耀,2003)。在当前对地球磁场高分辨率、高精度要求的背景下,地球变化磁场的研究对于地磁日变校正、空间天气监测预报、辅助导航的磁力图构建等都具有重要意义(牛超等,2021)。地磁观测容易受到外界干扰而导致数据缺测、漏测、错测,对其进行时间序列预测可以提高数据的可用性和连续性。
针对地磁场时间序列预测的方法主要分为数值预报方法和统计预报方法两类(刘博等,2021)。数值预报方法是根据先验知识和实际经验建立预测模型,其缺点是容易受到主观因素的影响。统计预报方法则是在大量数据驱动下进行数理统计分析,从而建立对应的输入与输出的函数关系,包括基于传统参数模型的时间序列预测方法和基于机器学习的时间序列预测方法,其中:基于传统参数模型的时间序列预测方法存在难以捕获数据的复杂非线性特征,在小样本泛化能力上表现不佳;基于机器学习的时间序列预测方法不仅可以避开其复杂的物理机制、挖掘数据中的有效信息、自动捕获隐藏的线性及非线性特征,还可以高效处理大规模时间序列数据(刘博等,2021)。
近年来,许多机器学习方法被引入地磁学研究领域。Sutcliffe (1999)首次将人工智能应用于地磁日变模型的开发;Yi等(2010)提出了建立地磁变化场多时间尺度组合模型的方法,该方法结合了可变地磁场的物理特征,融合了多个模型,且预测时间的跨度较长;Moghadam和Yaghoubi (2015)提出了一种区间情感神经网络(emotional neural network,缩写为ENN),并对Kp和Dst等地磁活动指数进行了预测;卢兆兴等(2021)通过构建反向传播(back propagation,缩写为BP)神经网络对地磁变化场的时均值数据进行了预测,经多次重复试验得到均方根误差为4.8 nT;程文凯等(2021)提出了基于优化分布式梯度提升库(extreme gradient boosting,缩写为XGBoost)的机器学习方法重构地磁日变数据,结果显示该方法的精度相较于反向传播神经网络更高。相较于传统的基于物理机制的模型,这些方法在地磁领域的应用提高了运算效率和预测精度,但是仍然存在分辨率不高、预测误差较大的问题。
地球变化磁场预测实质上是单变量时间序列预测问题,长短期记忆网络(long short-term memory,缩写为LSTM)在处理时间序列问题上优势明显,因此使用该网络来预测地磁场。但是仅靠LSTM无法达到需求的预测效果,考虑到地球变化磁场具有混沌特性以及信号中潜藏的高破坏性噪声信息,引入混沌理论和变分模态分解(variational mode decomposition,缩写为VMD)来去除噪声。故本文拟提出一种混沌VMD-LSTM预测方法,即地磁场数据经变分模态分解后,在变化磁场的重构相空间中,利用LSTM网络逼近相点的演化规律,对变化磁场进行预测,旨在提高预测分辨率和预测精度。
1. 理论方法
1.1 变分模态分解
变分模态分解(VMD)是一种通过求解频域变分优化问题来估计各信号分量的模态分解算法(Dragomiretskiy,Zosso,2014)。该算法的思路是假设目标信号可以拆分为一系列中心频率固定、带宽有限的子信号,各子信号即为本征模态函数。以经典的维纳滤波器为基础求解变分问题,得到中心频率和带宽限制,而后提取频域中各中心频率的有效成分,即所求模态函数。
假设地磁数据序列X是由K个有限带宽的固有模态分量uk(t)组成,K即分解层数,各模态的中心频率为ωk,约束条件为各模态相加之和等于原始信号输入,对各固有模态函数(intrinsic mode function, 缩写为IMF)进行希尔伯特变换,得到解析信号并计算单边谱,进而将各IMF分量中心频带调制到相应基带上,计算解调信号梯度的平方范数L2来估计各IMF的带宽,得到约束变分问题:
$$ \left\{ \begin{gathered} \min \left\{ {\sum\limits_{k = 1}^K {{{\left\| {{ {\text{∂}} _t}\left[ {\left( {\delta ( t ) + \frac{{\mathrm{j}}}{{\pi t}}} \right)*{u_k} ( t ) } \right]{{\mathrm{e}}^{ - {\mathrm{j}}{\omega _k}t}}} \right\|}^2}} } \right\} \text{,} \\ {\mathrm{s.t.}}\sum\limits_{k = 1}^K {{u_k}} = X \text{,} \\ \end{gathered} \right. $$ (1) 式中,δ(t)为狄拉克分布函数,j为虚数单位。求解上述方程,得到
$$ \hat u_k^{n + 1} ( \omega ) = \frac{{\hat X ( \omega ) - \displaystyle\sum\limits_{i {\text{≠}} k} {{{\hat u}_i} ( \omega ) } + \frac{{\hat \lambda ( \omega ) }}{2}}}{{1 + 2\alpha {{ ( \omega - {\omega _k} ) }^2}}} \text{,} $$ (2) $$ \omega _k^{n + 1} = \frac{{{{\displaystyle\int_0^\infty {\omega \left| {u_k^{n + 1} ( \omega ) } \right|} }^2}{\mathrm{d}}\omega }}{{{{\displaystyle\int_0^\infty {\left| {u_k^{n + 1} ( \omega ) } \right|} }^2}{\mathrm{d}}\omega }} \text{,} $$ (3) 式中:λ (t)为拉格朗日算子;α为二次惩罚因子,求解步骤详见Dragomiretskiy和Zosso (2014)。
VMD与其它模态分解算法相比有本质区别,且优势明显。VMD方法对采样噪声有较强的鲁棒性,可以有效避免端点效应和模态混叠。由于混杂在地磁变化数据中的噪声信号的不可预测性和高破坏性会掩盖系统本身的内在动力学特性(韩敏,2007),极大地影响了对系统的准确描述以及后续的精度预测,因此需要对地磁数据进行去噪处理。
1.2 混沌理论
混沌理论(chaos theory)是非线性系统在一定参数条件下展现分岔、周期与非周期运动相互纠缠,从而产生某种非周期有序运动的理论(Lorenz,1963)。
相空间重构是混沌理论的重要基础,用于从单一时间序列中发掘和恢复原系统的规律(李松,刘力军,2017)。假设地磁变化时间序列为{z1, z2, ···, zj, zi+(m-1)τ}(j=1, 2, ···, n),构造M=N-(m-1)τ个m维向量:
$$ {\boldsymbol{Z}} ( {{t_i}} ) = ( {{{\textit{z}}_i} \text{,} {{\textit{z}}_{i + \tau }} \text{,} \cdots \text{,} {{\textit{z}}_{i + ( m - 1 ) \tau }}} ) \text{,}\qquad {\textit{z}}_{i + ( m - 1 )} \in {{\mathrm{R}}^m} \text{,} $$ (4) 最终得到
$$ {\boldsymbol{Z}} ={ [ {{Z_{1} \text{,} }{Z_2}\text{,} \cdots \text{,} {Z_m}} ] ^{\mathrm{T}}} \text{,} $$ (5) 式中,m和τ分别为嵌入维数和延迟时间,Z为M×m维矩阵,本文采用伪最近邻域法和自相关函数法确定m和τ (韩敏,2007)。
地磁变化场起源于磁层和电流层体系,是一个十分复杂的系统,厘清其物理机理并建模完成预测几乎不可实现。考虑到变化磁场数据具有混沌特性(王赤等,1995),本文引入混沌理论来挖掘数据深层特征,以数据驱动寻找隐藏的规律从而完成预测。
1.3 长短期记忆网络
长短期记忆(LSTM)网络是一种时间递归神经网络(recursive neural network,缩写为RNN),具有记忆长短期信息的能力(Hochreiter,Schmidhuber,1997)。
传统的RNN网络无法记忆长期信息,且容易发生梯度消失和梯度爆炸现象。LSTM网络引入了“门”的机制来控制过程参数信息的流动和损失,有效解决了RNN的不足(Hochreiter,Schmidhuber,1997)。
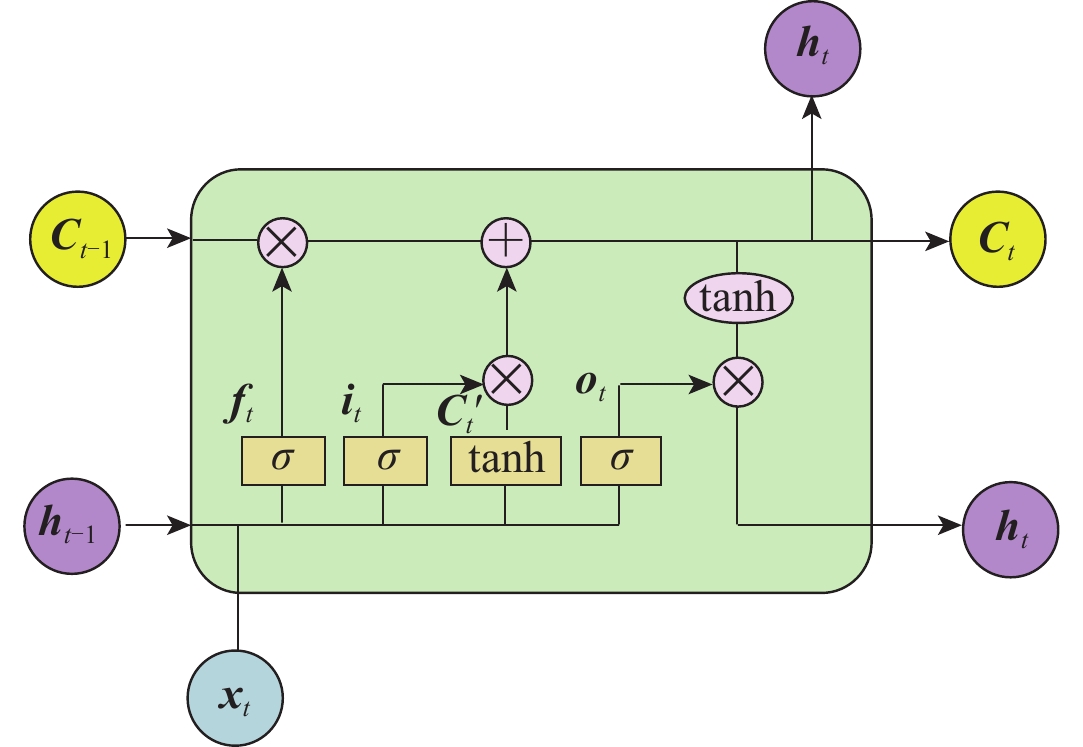
在RNN的基础上,LSTM网络在每个单元引入了三个“门”结构,分别是输入门、输出门和遗忘门,LSTM单元如图1所示。图中:${\boldsymbol{x}}_{t} $为单元输入数据;${\boldsymbol{h}}_{t} $为单元输出数据,${\boldsymbol{h}}_{t}={\boldsymbol{o}}_{t}{\mathrm{tanh}}C_{t}$,tanh为单元状态更新值的激活函数;${\boldsymbol{C}}_{t-1} $和${\boldsymbol{C}}_{t} $分别为上一单元和本单元的状态参数,${\boldsymbol{C}}_t { \text{′} }$为单元状态更新值,${\boldsymbol{C}}_t ={\boldsymbol{f}}_{t}{\boldsymbol{C}}_{t-1} +{\boldsymbol{i}}_{t}{\boldsymbol{C}}_t{ \text{′}} $。式中:${\boldsymbol{f}}_{t} $为遗忘门,是一个所有元素均位于$ [ 0 \text{,} 1 ] $内的向量,主要控制上一单元的状态参数${\boldsymbol{C}}_{t-1} $是否完整保留到本单元,通常以$\sigma $函数作为其激活函数,${\boldsymbol{f}}_{t} =\sigma ( W_{f} [ {\boldsymbol{h}}_{t-1}\text{,} {\boldsymbol{x}}_{t} ] +b_{f} ) $,W为权重,b为偏置;${\boldsymbol{i}}_{t} $为输入门,与遗忘门相同,是一个元素均位于$ [ 0 \text{,} 1 ] $内的向量,主要控制输入数据对本单元状态的影响程度,由单元输入${\boldsymbol{x}}_{t} $和隐节点${\boldsymbol{h}}_{t-1} $经$\sigma $函数激活得到,${\boldsymbol{i}}_{t} =\sigma ( W_{i} [ {\boldsymbol{h}}_{t-1}\text{,} {\boldsymbol{x}}_{t} ] +b_{i} ) $;${\boldsymbol{o}}_{t} $为输出门,其计算方法与${\boldsymbol{f}}_{t} $和${\boldsymbol{i}}_{t} $相同,主要控制本单元状态有多少参与输出,${\boldsymbol{o}}_{t} =\sigma ( W_{o} [ {\boldsymbol{h}}_{t-1}\text{,} {\boldsymbol{x}}_{t} ] +b_{o} ) $。
LSTM网络可以有效地捕捉地磁数据的长期变化和短期瞬时变化,可以在地磁变化预测上发挥较大作用。
2. 预测模型构建
2.1 VMD算法去噪
VMD分解的效果主要受分解层数K影响:当K值较小时,由于VMD算法相当于自适应滤波器组,原始信号中部分信息会被过滤,因而影响后续的预测精度;而当K值较大时,相邻模态的中心频率会相距较近,导致模态混叠或产生额外的噪声(郑小霞等,2017)。因此进行VMD分解之前,首要的是确定分解层数K。
确定分解层数常用的方法为中心频率法,不同模态的区别主要在于中心频率的差异。中心频率法即通过对不同模态下中心频率的分布情况进行观察(陶凯,吴定会,2021),进而选取合适的K值。但是中心频率法确定的分解层数有时会偏大,产生过分解现象,即分解所得有效模态中出现白噪声信号等无效成分,导致分解效果变差。
因此本文应用样本熵和相关系数来解决过分解的问题,具体步骤如下:
1) 根据中心频率法确定分解层数初值K0。
2) 计算分解层数为K0时的样本熵值,判断是否发生过分解现象。样本熵是表征信号序列复杂程度的无量纲指标,熵值越大,信号复杂度越大(Xie et al,2008)。当VMD 提取到信号的有效分量时,对应的样本熵值理应较小,并且与相邻分量的样本熵存在显著差异,而噪声分量由于其无规律性,熵值相对较大。当出现过分解现象时,部分相邻分量的样本熵相近。因此,可借助样本熵来判别是否存在过分解问题,计算方法如下:
① 设原数据集{Xi}={x1,x2,···,xN},N为数据长度。给定嵌入维数m和相似容限r,据此将原始信号重构为m维向量${{{\boldsymbol{x}}}} ( i ) = [ {x_i}\text{,} {x_{i + 1}}\text{,} \cdots \text{,} {x_{i + m - 1}} ] \text{,} i = 1\text{,} 2\text{,} \cdots \text{,} N - m$;② 计算每个向量与其它向量的距离dij并统计其中dij<r的数据及该数据与dij总个数的比值,记为$ B_i^m ( r ) $,
$$ {d_{ij}} = d [ {\boldsymbol{x}} ( i ) \text{,} {\boldsymbol{x}} ( j ) ] = \mathop {\max }\limits_{k \in [ 0\text{,} m - 1 ] } \left| {{\boldsymbol{x}} ( i + k ) \text{,} {\boldsymbol{x}} ( j + k ) } \right| \text{,} $$ (6) $$ {B}_{i}^{m} ( r ) = \frac{1}{N-m-1}\{{d}_{ij} {\text{<}} r的个数\} ;$$ (7) ③ 计算$ B_i^m ( r ) $的平均值
$$ {B^m} ( r ) = \frac{1}{{N - m}}\sum\limits_{i= 1}^{N - m} {B_i^m ( r ) } \text{;} $$ (8) ④ 提高嵌入维数到m+1,重复前四步,得到$ {B^{m + 1}} ( r ) $;
⑤ 求样本熵
$$ {\mathrm{SampEn}} ( m\text{,} r ) = \mathop {\lim }\limits_{N \to \infty }\left[ - \ln \frac{{{B^{m + 1}} ( r ) }}{{{B^m} ( r ) }}\right] \text{,} $$ (9) 式中,m一般取2,r一般取0.1—0.25倍的原数据标准差。若N有限,样本熵公式变为
$$ {\mathrm{SampEn}} ( m\text{,} r\text{,} N ) = \ln {B^m} ( r ) - \ln {B^{m + 1}} ( r ) .$$ (10) 3) 若未发生过分解现象,则K=K0;若发生过分解,则计算残余分量与有效成分的相关系数,取相关系数绝对值最小时的分解层数Kmin即为最佳分解层数。原始数据减去经去噪的有效成分即为残余分量,当残余分量与去噪信号相关性最低时,残余分量中包含最多影响预测结果的噪声成分。
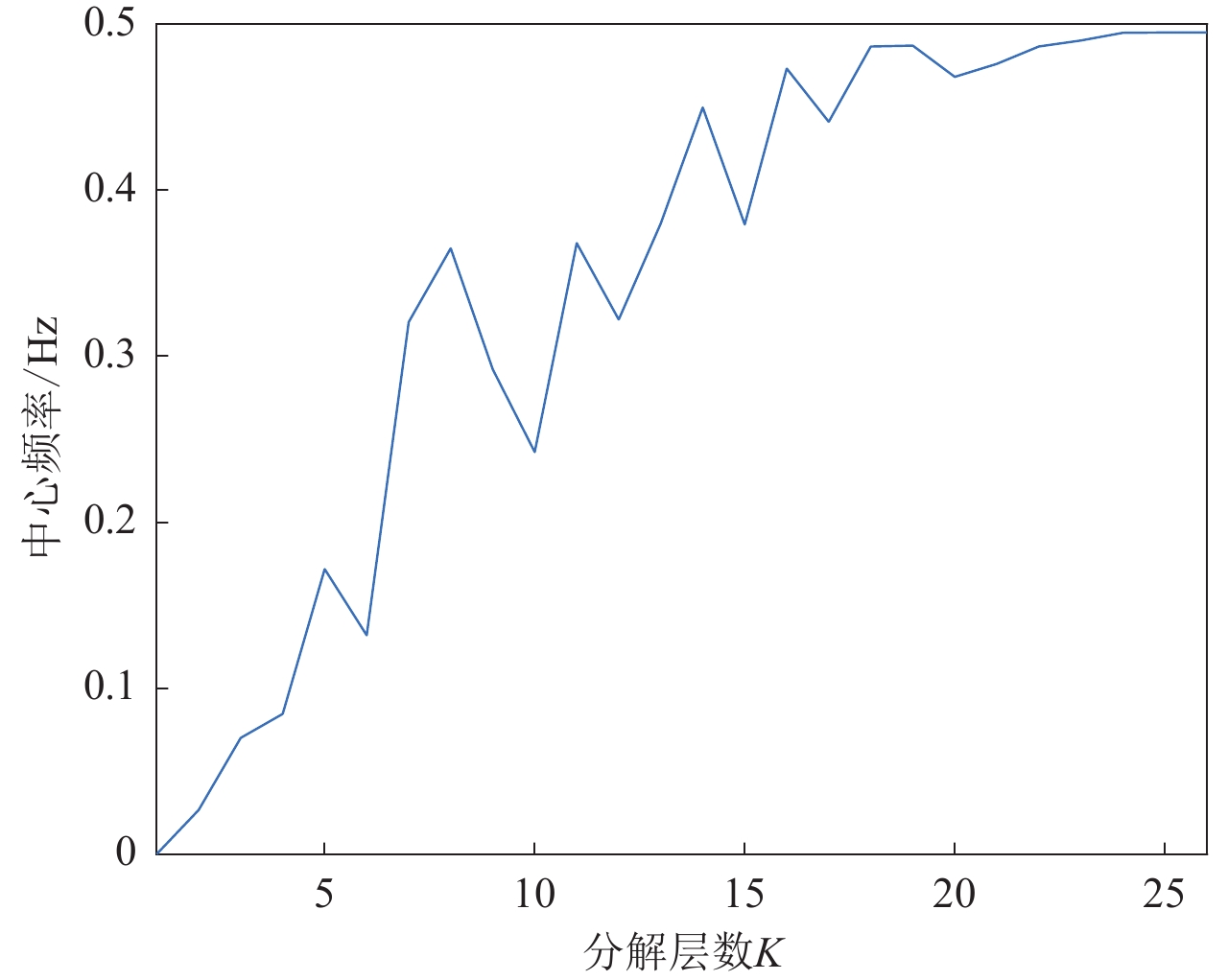
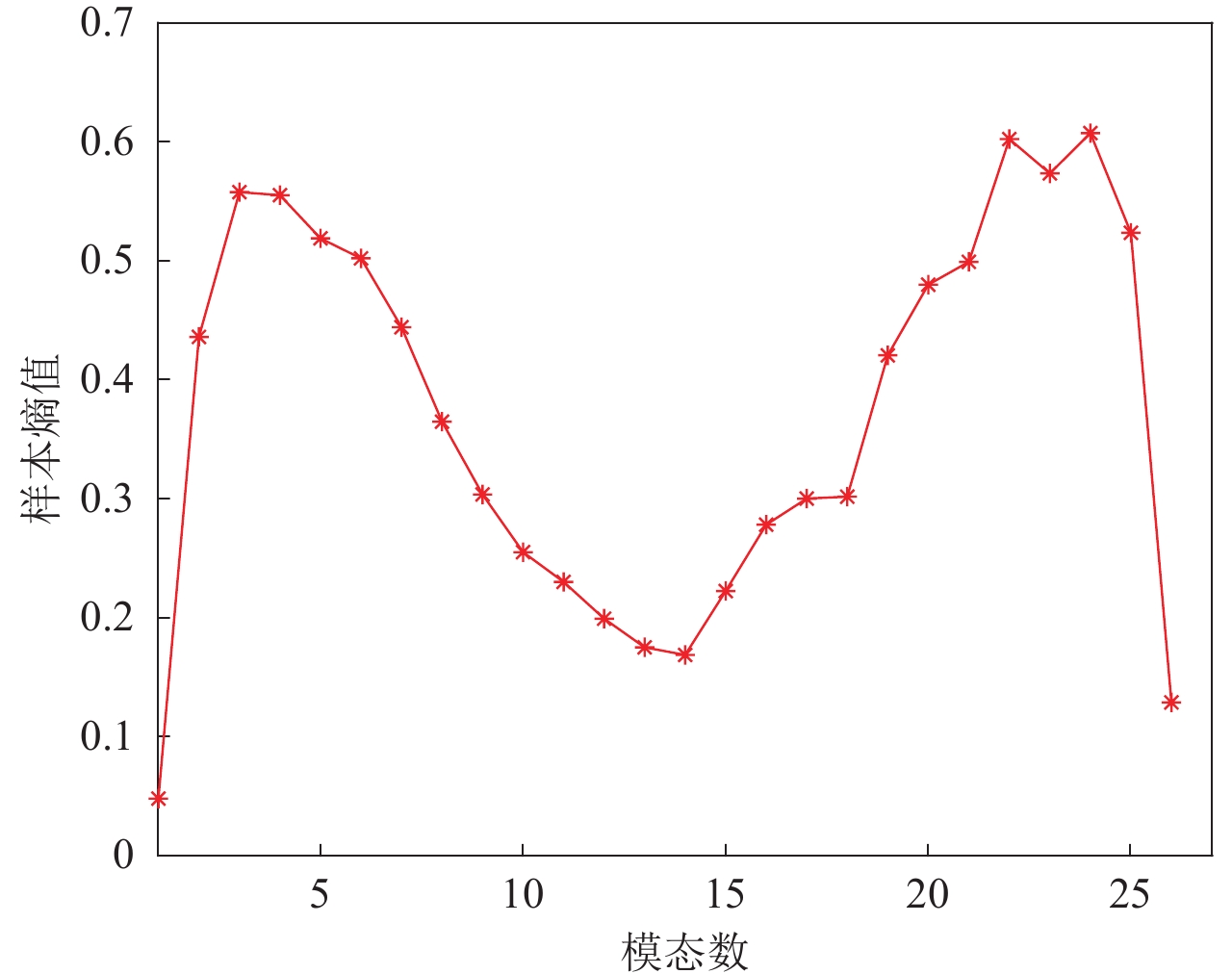
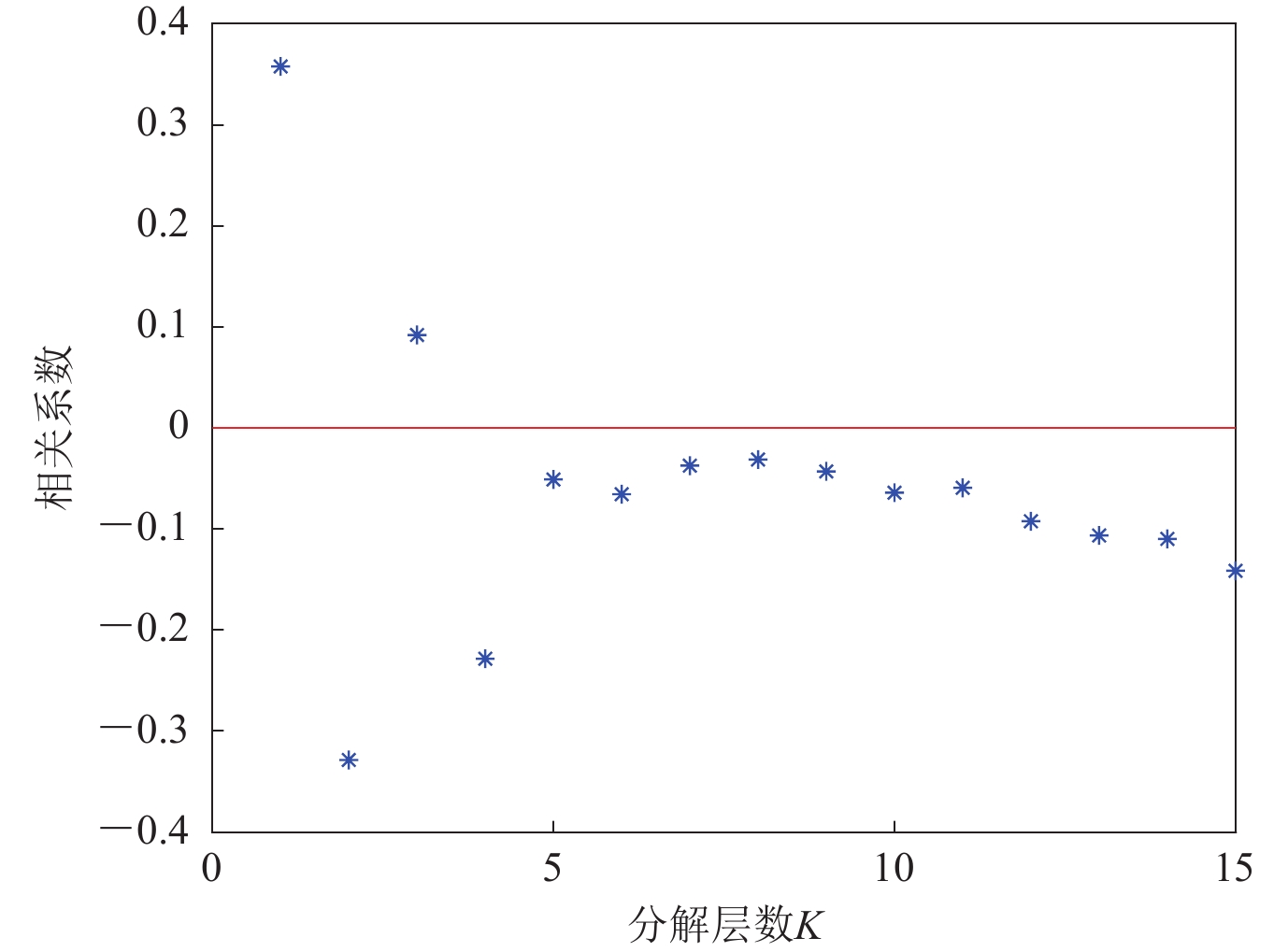
下面以广州肇庆站2020年3月6日的实测数据进行验证。首先计算中心频率,结果如图2所示。由该图可见,随着分解层数的增加,中心频率呈波动上升趋势,直到K=24时,中心频率才趋于稳定,即使用中心频率法确定的分解层数为24。计算此时的各模态样本熵,结果如图3所示。可见,K=24时各模态分量的样本熵曲线呈驼峰状,且9到17模态的熵值十分接近,差值小于0.1。由此可以判定,分解层数为24时发生过分解现象。下面计算残余分量与去噪数据的相关系数,结果如图4所示。可以看到,当K=8时,残余分量与去噪信号的相关性最低,随着K值增大,相关系数的绝对值反而增大,这说明使用中心频率法计算出的K值存在过分解现象。经计算相关系数确定分解层数为8,此时去噪数据与原始数据相比,绝对误差约为0.2 nT,相对误差为0.03%,误差较小,能够在降低数据复杂度的前提下保证信息的完整性。因此本文提出的联合中心频率法、样本熵算法和相关系数的做法可为确定最佳分解层数提供新思路。
2.2 混沌相空间重构
确定地磁变化场序列存在混沌特性后,首先对时间序列进行相空间重构,步骤如下:
1) 采用最大李雅普诺夫法(Vastano,Kostelich,1986)对去噪后的数据进行混沌特性检验;
2) 采用自相关函数法确定延迟时间τ。对于地磁变化序列{zj} (j=1,2,···,n),其时间跨度为jτ,自相关函数定义为:
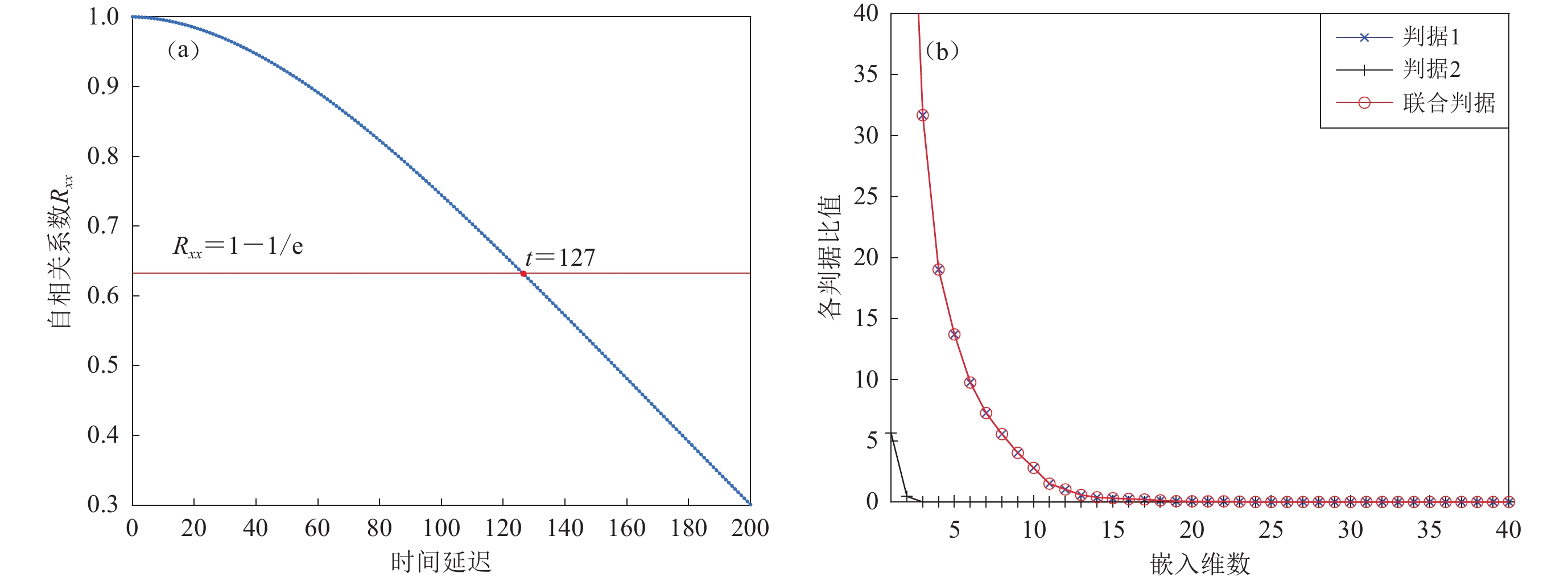
$$ {R_{xx}} ( {j\tau } ) = \frac{1}{N}\sum\limits_{t = 0}^{N - 1} {x ( t ) x ( {t + j\tau } ) } .$$ (11) 固定j,绘出Rxx关于时间τ的函数图像。当Rxx下降至初始值的(1-1/e)倍时,所得时间τ即为所求延迟时间(韩敏,2007)。
3) 采用伪最近邻域法确定嵌入维数m。在地磁数据重构后的m维相空间中,每个相点$Z ( t ) =\left\{{\textit{z}} ( t ) \text{,} {\textit{z}} ( t+\tau ) \text{,} \cdots \text{,} {\textit{z}} [ t+ ( m-1 ) \tau ] \right\}$都存在某个距离内最近邻点ZF,采用欧式度量计算Z(t)与ZF(t)两相点间距$R_{m} ( t ) =\left\| {Z ( t ) -Z_{{\mathrm{F}}} ( t ) }\right\|$。将m维相空间扩展到m+1维,两相点的间距则变为
$$ R_{m + 1}^2 ( t ) = R_m^2 ( t ) + {\left\| {Z ( {t + m\tau } ) - {Z_F} ( {t + m\tau } ) } \right\|^2} .$$ (12) 如果$ {R_{m + 1}} ( t ) $与$ {R_m} ( t ) $相差较大,则可认为这是因为高维混沌吸引子的两个邻点在投影到低维空间时变成了伪最近邻点。令
$$ {S_{ m}} = \frac{{\left\| {Z ( {t + m\tau } ) - {Z_{\mathrm{F}}} ( {t + m\tau } ) } \right\|}}{{{R_m} ( t ) }} \text{,} $$ (13) 若Sm>ST,则判定ZF (t)是Z (t)的虚假最近邻点,ST为阈值,可在$ [10\text{,} 50] $之间选择。由于样本个数有限且受噪声影响,重构相点与邻近点相距不近,因此比较相点与序列方差Ra,得到判据1为
$$ \frac{{{R_m} ( n ) }}{{{R_a}}} {\text{≥}} 2 \text{;} $$ (14) 判据2为 m+1维相空间与m维欧氏距离的比值大于阈值${S_{ \mathrm{T}}}$,即
$$ \frac{{{R_{m + 1}} ( n ) }}{{{R_m} ( n ) }} {\text{≥}} R .$$ (15) 二者同时满足即为联合判据。从最小嵌入维数m0开始计算联合判据取值,然后逐渐增大m,当m增大至比值小于5%或者不随嵌入维数的增加而减小时,可以认为奇异吸引子已经完全展开,此时的m即为最佳嵌入维数(韩敏,2007)。
4) 进行混沌相空间重构,得到重构数据集。
2.3 混沌VMD-LSTM组合预测方法
1) 将已知的地磁变化垂向分量数据作为预测的原始时间序列,基于数据确定分解层数K等相关参数,对原始数据进行VMD分解去噪得到优化后的数据。
2) 根据混沌理论中的伪最近邻域法和自相关函数法,计算经VMD优化的地磁变化序列的嵌入维数m和延迟时间τ,然后进行相空间重构,得到经混沌参数优化的数据集$ {\boldsymbol{Z}} ={ [ {{Z_{1}}\text{,} {Z_2}\text{,} \cdots\text{,} {Z_m}} ] ^{\mathrm{T}}} $,将$ Z ( {{t_i}} ) = ( {{{\textit{z}}_i}\text{,} {{\textit{z}}_{i + \tau }}\text{,} \cdots \text{,} {{\textit{z}}_{i + ( m - 1 ) \tau }}} ) $作为LSTM网络的输入数据,其中${{\textit{z}}_{i + ( m - 1 )} \in {\mathrm{R}}^m} $。
3) 利用前两步优化后的训练样本对LSTM网络进行训练,以m为基准改变嵌入维数并反复训练,达到最佳训练效果,据此构建LSTM网络,最终通过测试样本得到地磁变化垂向分量的预测数据。
3. 方法验证
3.1 试验数据
垂向分量Z和磁倾角I相对于其它地磁分量预测难度较小(齐玮等,2010),角度类分量I在广泛的中纬度地区变化较小,在我国范围内不宜用作导航匹配特征量(乔玉坤等,2007),因此本文选用磁通门磁力仪测得的地球变化磁场垂向分量数据Z作为试验对象,对于其它地磁分量的研究将在后续开展。
本文使用的实测数据来自子午工程数据中心提供的网上公开数据集,分辨率为1 min,包括广州肇庆站(ZQT)、北京十三陵站(SSL)、四川郫县站(PXT)、黑龙江漠河站(MHT)、西藏拉萨站(LAT)等五个台站。时间跨度过2020年3月1日至3月9日,共有1万2 960个样本点,其中以样本集前9 600个数据训练预测模型,后3 360个数据为预测检验样本集。
3.2 评价指标
本文采用平均绝对误差(mean absolute error,缩写为MAE)、均方根误差(root mean square error,缩写为RMSE)、平均绝对百分比误差(mean absolute percentage error,缩写为MAPE)、相关指数R2、调整后的相关系数(adjusted_R2,缩写为Ad_R2)、相对准确率(relative accuracy,缩写为RA)等6个指标来评价所提出预测方法的效果,计算公式如下:
$$ {\mathrm{MAE}}= \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|}\text{,} $$ (16) $$ {\mathrm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{ ( {{y_i} - {{\hat y}_i}} ) }^2}}} \text{,} $$ (17) $$ {\mathrm{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right|}\text{,} $$ (18) $$ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{ ( {{y_i} - {{\hat y}_i}} ) }^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{ ( {{y_i} - \overline y} ) }^2}} }}\text{,} $$ (19) $$ {\mathrm{Ad}}\_{R^2} = 1 - \frac{{ ( {n - 1} ) \left( {1 - {R^2}} \right)}}{{n - p - 1}} \text{,} $$ (20) $$ {\mathrm{RA}} = 1 - \frac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{{y_i}}}\text{,} $$ (21) 式中,$ {y_i} $为台站实测地磁变化数据,$ {\hat y_i} $为预测所得地磁变化数据,$\overline y$为实测数据的均值。
3.3 广州肇庆站模型预测
广州肇庆站的建模及预测主要分为以下几步:
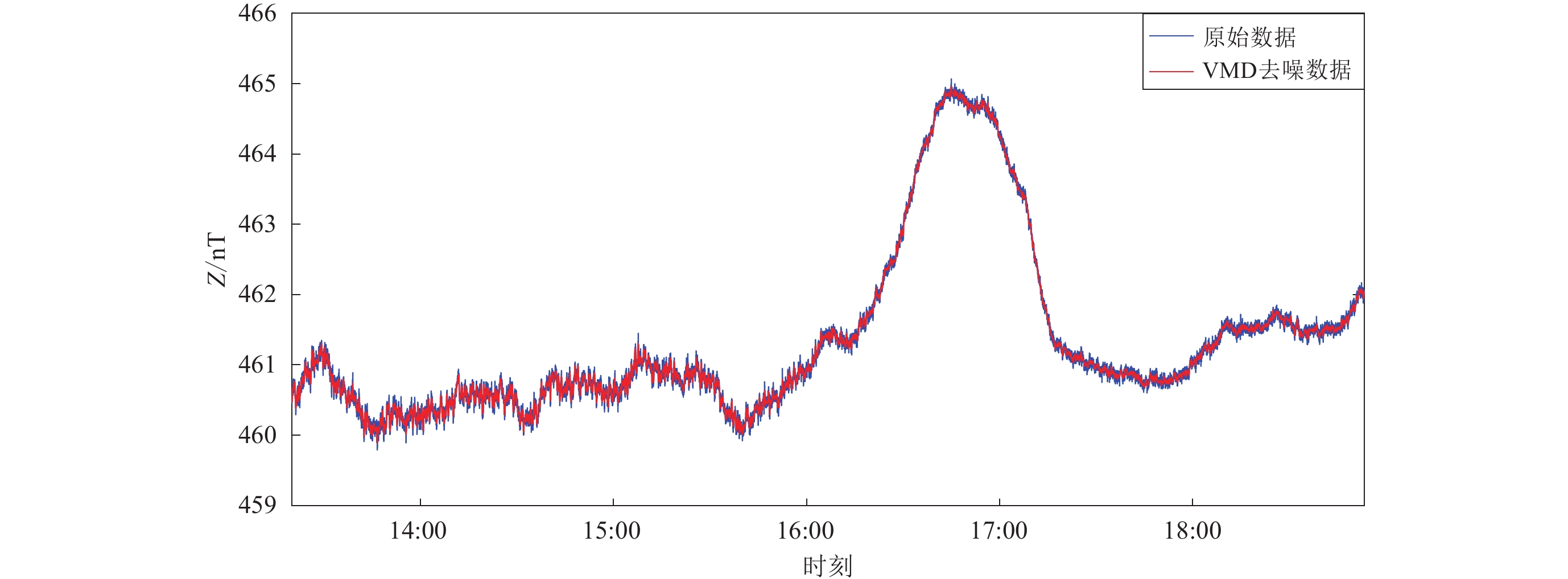
1) VMD去噪。由中心频率法结合样本熵、相关系数求得最佳分解层数K=8。设置VMD分解的其它参数:带宽限制ɑ=2 000,噪声容限τ=0.024 4,无直流部分DC=0,中心频率均匀初始化init=1,迭代停止的指示值ε=10−7。对原始数据进行VMD分解得到去噪后的信号,如图5所示。可见,经过改进VMD去噪后,有效滤除了具有明显随机性的测量误差,提高了数据的可预测性。
2) 混沌相空间重构。由伪最近邻域法和自相关函数法绘制参数判断过程图,如图6a所示。当自相关函数下降到初始值的1-1/e倍时,所得时间即为最佳延迟时间,由图6a可见去噪信号的时间延迟τ=127。由图6b可知,当联合判据减小到最小时,嵌入维数m=20。以此为参考,对去噪后的信号进行相空间重构,最终得到经去噪重构处理的数据集,以该数据集作为LSTM网络训练集和测试集。
3) LSTM预测及结果分析。搭建LSTM网络,令输入层与嵌入维数保持一致,均为20维,隐含层单元数为96×3,输出为一维向量,设置求解器为adam函数,梯度阈值为1,迭代200次,初始学习率为0.005,在125轮训练后通过乘以因子0.2来降低学习率。将优化后的数据集中前9 600个数据作为训练样本集,后3 360个数据作为需要预测的未知样本。选取训练集中最后(m-1)τ+1个数据作为预测输入样本进行单步递推预测,得到预测结果。
为了验证本文所提方法的有效性及预测精度,使用相同的输入输出数据集分为两部分进行对比,一部分将本文用到的方法分别组合形成单一LSTM网络、混沌LSTM、VMD-LSTM三个模型来进行预测,另一部分使用传统的时间序列预测模型进行预测,包括自回归差分移动平均模型(auto-regressive integrated moving average model,缩写为ARIMA)和灰色模型(grey model,缩写为GM),对比结果如图7所示。为了消除偶然性,每次试验均重复多次,其中ARIMA和GM模型结果固定,无需重复进行,且随预测时长的增大,预测结果呈线性趋势发展,与原值偏离较大,因此为观察其预测细节,仅绘制预测时长为2 h的图像。
图7a和7b分别为传统LSTM神经网络直接预测和先经过VMD去噪再进行LSTM预测的结果,可见两方法的预测最终均趋于一个常值,且该常值具有随机性,这可能是由于模型采用LSTM单步迭代预测策略所致。即不断地把输入样本集的第一个元素剔除、并不断地把未来预测值作为输入集的最后一个元素,如此这样不断地往后滚动样本集来实现滚动的单步预测。由于数据量较大,而该预测方法存在误差累积的问题,因此随着滚动预测次数的增加,误差逐渐累积,导致数据变化趋势稳定,表明传统的LSTM模型在进行多步地磁变化数据预测上效果不佳。
图7c是混沌理论优化后进行LSTM预测的结果,相较于图7a和图7b,其结果的精度明显较高,能够较好地捕捉到地磁变化场的变化趋势,但是该模型存在容易发散的问题,对于变化细节的预测不够准确。
图7e和7f为ARIMA和GM模型的预测结果。ARIMA模型对于预测前30 min可以得到相对准确的结果,30 min到2 h仅能预测变化趋势,2 h以后模型趋势固定,完全失去预测能力(图7e),这可能是由于ARIMA模型只考虑自身滞后项和扰动项对曲线的影响,而忽略了其它因素的干扰。GM模型预测效果偏差(图7f),这可能是由于本文所用模型为简单的GM (1,1)所致,该模型的优势在于展示未来较长时期的走势,而对复杂曲线的变化预测效果较差。
图7d是本文提出的混沌VMD-LSTM模型,其预测精度明显高于其它方法。虽然本模型也仅依靠单序列数据进行预测,看似与ARIMA模型存在相同的缺陷,但模型引入了混沌相空间重构方法,还原了高维吸引子的内在规律,实际上已经将混沌系统中影响预测对象的其它影响因素考虑在内。在混沌理论优化的核心框架下引入VMD去除影响预测精度的高破坏性噪声,既能有效地预测地磁变化场的变化趋势,又能较好地处理变化细节,并且经多次重复试验能够得到较为收敛的有效预测结果。
为了更好地验证本文方法的有效性,计算了六个模型的误差评价指标,多次重复试验取均值,结果列于表1。可见:本文提出的混沌VMD-LSTM方法预测精度显然远超过其它模型;混沌VMD-LSTM模型的平均绝对误差小于2 nT,与混沌LSTM相比提高了34.24%,与ARIMA和GM模型相比分别提升了85.82%和84.13%;混沌VMD-LSTM方法的均方根误差小于3 nT,与混沌LSTM相比提高了39.47%,与ARIMA和GM模型相比分别提高了82.35%和80.66%;混沌VMD-LSTM方法的平均绝对百分比误差仅为0.4%,达到了较高的预测精度。相关系数R2刻画了预测数据拟合实测数据的效果,为了避免由于数据样本量过大产生的误差过大,采用Ad_R2来估计相关指数。一般Ad_R2超过0.8即达到了较好的拟合效果,混沌VMD-LSTM方法的R2超过了0.85,达到了较高的拟合程度,与其它模型相比优势明显。综上,本文提出的混沌VMD-LSTM方法可以较好地预测出未来的地磁变化趋势,表明该模型是一种比较有效的地磁变化场估计方法。
表 1 地磁变化预测评估Table 1. Evaluation of geomagnetic variation prediction预测方法 MAE/nT RMSE/nT MAPE R2 Ad_R2 RA 单一长短期记忆(LSTM) 6.945 0 9.592 8 0.154 0 0.622 7 0.837 4 0.984 6 VMD-LSTM 6.815 9 9.118 5 0.151 0 0.459 5 0.853 8 0.984 9 混沌优化LSTM 2.944 3 4.752 9 0.006 5 0.614 8 0.612 6 0.993 4 混沌VMD-LSTM 1.936 2 2.876 8 0.004 0 0.854 3 0.853 4 0.995 7 自回归差分移动平均模型 13.655 9 16.298 9 0.030 1 0.346 6 0.349 3 0.969 9 灰色模型 12.197 3 14.872 0 0.026 9 0.271 8 0.274 0 0.973 1 注: MAE为平均绝对误差,RMSE为均方根误差,MAPE为平均绝对百分比误差,R2为相关指数,Ad_R2为调整后的相关系数,RA为相对准确率,下同。 3.4 泛用性评估
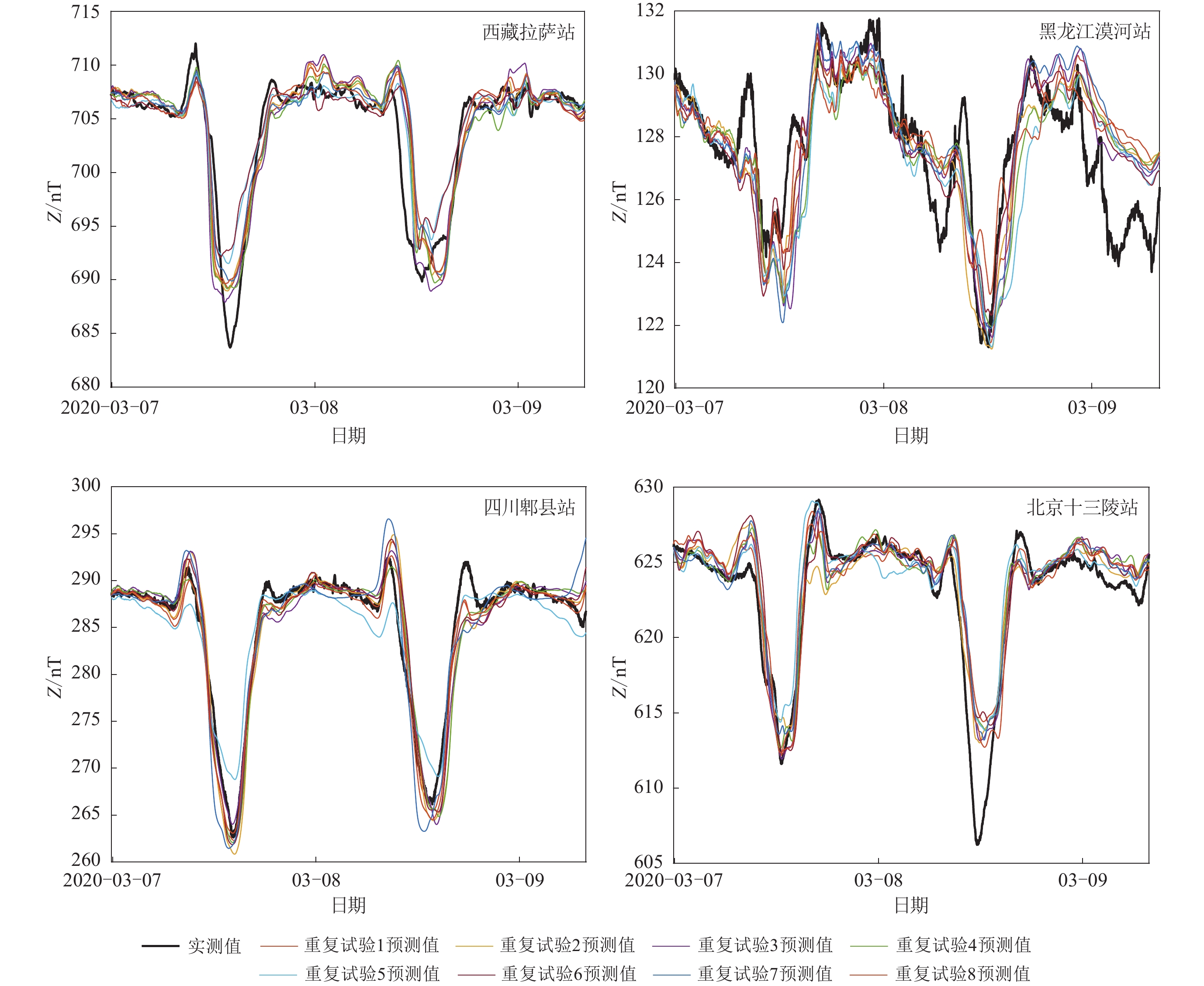
为了评估文中提出的方法在我国其它区域的适用性,按照与广州肇庆站建模同样的方法和步骤对北京十三陵站(SSL)、四川郫县站(PXT)、黑龙江漠河站(MHT)、西藏拉萨站(LAT)的地磁数据分别进行重新建模预测(图8)并计算相应的评价指标(表2)。
表 2 各台站预测评估误差Table 2. Evaluation error of prediction results for several stations台站 MAE/nT RMSE/nT MAPE R2 Ad_R2 RA 拉萨站(LAT) 1.705 1 2.714 7 0.002 4 0.802 2 0.801 0 0.997 5 漠河站(MHT) 1.256 3 1.628 6 0.009 9 0.465 6 0.462 4 0.990 0 郫县站(PXT) 1.499 9 2.184 0 0.005 3 0.905 2 0.904 7 0.994 7 十三陵站(SSL) 1.309 7 1.952 5 0.002 1 0.820 5 0.819 5 0.997 9 如图8所示,总体来看,在北京十三陵站、四川郫县站、黑龙江漠河站、西藏拉萨站这四个站点,混沌VMD-LSTM方法均可以较准确地反映地磁场的变化趋势,MAE均小于2 nT,RMSE不超过2.8 nT,除漠河站外,R2均超过0.8,相对准确率均超过99%,拟合度较高。比较四个站点,拉萨站预测较实测值略有滞后,漠河站所选时间段地磁活动剧烈,地磁变化复杂度较高,预测效果相对较差,十三陵站预测效果较好,3月8日极小值预测稍有偏差,郫县站预测效果最好。因此,本文提出方法在中国大陆区域弱地磁活动时期均有较好预测效果,可以推广到其它台站。
3.5 时效性评估
预报时效是天气预报的有效期限,参照该定义,地磁变化预测模型的有效预测时长则为模型预测时效。本节使用调整后的相关指数Ad_R2作为预测时效的评判指标(王鹏飞等,2015),若一段时间$ {\mathrm{Ad}}\_{R^2} {\text{≥}} 0.8 $,则认为该时段为有效预测时段。试验设置预测时长为1天、2天、2.5天、3天和7天,取各台站多次重复试验平均值,结果如表3所示。可见,训练样本集为7天数据时,本文所建混沌VMD-LSTM模型的有效预测时间最长可以达到2.5天,在2.5天之后预报时效逐渐降低。
表 3 模型的预测时效Table 3. Model prediction timeliness预测时长/d Ad_R2 1 0.89 2 0.83 2.5 0.80 3 0.72 7 0.60 4. 讨论与结论
针对地磁变化场时间序列的复杂性,本文提出了一种基于混沌VMD-LSTM神经网络的地球变化磁场组合预测方法。首先对地磁变化序列进行VMD分解去噪,降低原始序列的非平稳性和非线性,然后对去噪数据进行混沌相空间重构,恢复其混沌吸引子,最后将重构数据划分为训练集和测试集,以LSTM网络进行单步迭代预测,最终得到地磁变化场的多步预测结果。
结果表明,VMD有效地去除了原数据中高破坏性的噪声信号,降低了系统的复杂度,提高其可预测性,混沌理论较好地还原了地磁变化的内在规律,大大提高了预测的精度。本文提出的预测方法具有很高的预测精度,平均预测结果最大MAE不超过2 nT,RMSE小于2.8 nT,MAPE低于0.5%,Ad_R2超过0.8,有效预测时长可达2.5天,且在我国大陆泛用性较好,因此可以推广到其它台站,为地磁辅助导航等相关研究提供便利。
由于VMD去噪和混沌相空间重构都需要事先确定其关键参数,关键参数的选取直接影响最终的预测精度,本文确定参数的方法均为传统方法,在后续工作中考虑应用先进的适配地磁变化预测的智能优化算法,来提高参数选取的准确率并减少模型训练时间。本文在选用台站数据时未关注磁扰问题,预测性能是否受到磁扰程度的影响,怎样减少磁扰的影响等是后续研究的重点。另外,本文方法对于垂向分量以外的其它分量的适用性以及不同地磁分量的针对性改进等也是后续开展研究的方向。
-
表 1 地磁变化预测评估
Table 1 Evaluation of geomagnetic variation prediction
预测方法 MAE/nT RMSE/nT MAPE R2 Ad_R2 RA 单一长短期记忆(LSTM) 6.945 0 9.592 8 0.154 0 0.622 7 0.837 4 0.984 6 VMD-LSTM 6.815 9 9.118 5 0.151 0 0.459 5 0.853 8 0.984 9 混沌优化LSTM 2.944 3 4.752 9 0.006 5 0.614 8 0.612 6 0.993 4 混沌VMD-LSTM 1.936 2 2.876 8 0.004 0 0.854 3 0.853 4 0.995 7 自回归差分移动平均模型 13.655 9 16.298 9 0.030 1 0.346 6 0.349 3 0.969 9 灰色模型 12.197 3 14.872 0 0.026 9 0.271 8 0.274 0 0.973 1 注: MAE为平均绝对误差,RMSE为均方根误差,MAPE为平均绝对百分比误差,R2为相关指数,Ad_R2为调整后的相关系数,RA为相对准确率,下同。 表 2 各台站预测评估误差
Table 2 Evaluation error of prediction results for several stations
台站 MAE/nT RMSE/nT MAPE R2 Ad_R2 RA 拉萨站(LAT) 1.705 1 2.714 7 0.002 4 0.802 2 0.801 0 0.997 5 漠河站(MHT) 1.256 3 1.628 6 0.009 9 0.465 6 0.462 4 0.990 0 郫县站(PXT) 1.499 9 2.184 0 0.005 3 0.905 2 0.904 7 0.994 7 十三陵站(SSL) 1.309 7 1.952 5 0.002 1 0.820 5 0.819 5 0.997 9 表 3 模型的预测时效
Table 3 Model prediction timeliness
预测时长/d Ad_R2 1 0.89 2 0.83 2.5 0.80 3 0.72 7 0.60 -
程文凯,杜劲松,陈超,艾萨·伊斯马伊力. 2021. 基于XGBoost机器学习的地磁日变重构方法研究[J]. 地震学报,43(1):100–112. Cheng W K,Du J S,Chen C,Yisimayili A. 2021. Reconstruction method for diurnal variations of the geomagnetic field by XGBoost machine learning[J]. Acta Seismologica Sinica,43(1):100–112 (in Chinese).
韩敏. 2007. 混沌时间序列预测理论与方法[M]. 北京:中国水利水电出版社:79−92. Han M. 2007. Prediction Theory and Method of Chaotic Time Series[M]. Beijing:China Water Resources and Hydropower Press:79−92 (in Chinese).
李松,刘力军. 2017. 混沌时间序列智能预测方法及其应用[M]. 北京:科学出版社:17−27. Li S,Liu L J. 2017. Intelligent Forecasting of Chaotic Time Series and Its Application[M]. Beijing:Science Press:17−27 (in Chinese).
刘博,王明烁,李永,陈洪丽,李建强. 2021. 深度学习在时空序列预测中的应用综述[J]. 北京工业大学学报,47(8):925–941. Liu B,Wang M S,Li Y,Chen H L,Li J Q. 2021. Deep learning for spatio-temporal sequence forecasting:A survey[J]. Journal of Beijing University of Technology,47(8):925–941 (in Chinese).
卢兆兴,吕志峰,李婷,张金生,姚垚. 2021. 基于BP神经网络的地磁变化场预测研究[J]. 大地测量与地球动力学,41(3):229–233. doi: 10.14075/j.jgg.2021.03.002 Lu Z X,Lü Z F,Li T,Zhang J S,Yao Y. 2021. Forecasting of the variable geomagnetic field based on BP neural network[J]. Journal of Geodesy and Geodynamics, 41 (3):229−233 (in Chinese).
牛超,李夕海,魏一苇,刘代志. 2021. 区域地磁变化场分析与建模关键技术研究[M]. 西安:西安电子科技大学出版社:1−2. Niu C,Li X H,Wei Y W,Liu D Z. 2021. Research on Key Technology of Regional Geomagnetic Variation Field Analysis and Modeling[M]. Xi’an:Xidian University Press:1−2 (in Chinese).
齐玮,王秀芳,李夕海,刘代志. 2010. 基于统计建模的地磁匹配特征量选择[J]. 地球物理学进展,25(1):324–330. Qi W,Wang X F,Li X H,Liu D Z. 2010. Selection of characteristic components for geomagnetic matching based on statistical modeling[J]. Progress in Geophysics,25(1):324–330 (in Chinese).
乔玉坤,王仕成,张琪. 2007. 地磁匹配特征量的选择[J]. 地震地磁观测与研究,28(1):42–47. doi: 10.3969/j.issn.1003-3246.2007.01.007 Qiao Y K,Wang S C,Zhang Q. 2007. Selection of characteristic variable of geomagnetism for matching[J]. Seismological and Geomagnetic Observation and Research,28(1):42–47 (in Chinese).
陶凯,吴定会. 2021. 基于VMD-JAYA-LSSVM的短期风电功率预测[J]. 控制工程, 28 (6):1143−1149. Tao K,Wu D H. 2021. Short-term wind power prediction based on VMD-JAYA-LSSVM[J]. Control Engineering of China, 28 (6):1143−1149 (in Chinese).
王赤,陈金波,王水. 1995. 地球变化磁场的分形和混沌特征[J]. 地球物理学报,38(1):16–24. Wang C,Chen J B,Wang S. Fractal and chaotic features for varying component of the Earth’s magnetic field[J]. Chinese Journal of Geophysics, 38 (1):16−24 (in Chinese).
王鹏飞,丁兆敏,林鹏飞,黄刚. 2015. 时间滑动相关方法在SST可预报性及可信计算时间研究中的应用[J]. 气候与环境研究,20(3):245–256. Wang P F,Ding Z M,Lin P F,Huang G. 2015. Application of the sliding temporal correlation approach to the studies of predictability and reliable computation time of sea surface temperature.[J]. Climatic and Environmental Research,20(3):245−256 (in Chinese).
徐文耀. 2003. 地磁学[M]. 北京:地震出版社:221. Xu W Y. 2003. Geomagnetism[M]. Beijing:Seismological Press:221 (in Chinese).
郑小霞,周国旺,任浩翰,符杨. 2017. 基于变分模态分解和排列熵的滚动轴承故障诊断[J]. 振动与冲击,36(22):22–28. Zheng X X,Zhou G W,Ren H H,Fu Y. 2017. A rolling bearing fault diagnosis method based on variational mode decomposition and permutation entropy[J]. Journal of Vibration and Shock,36(22):22–28 (in Chinese).
Dragomiretskiy K,Zosso D. 2014. Variational mode decomposition[J]. IEEE Trans Signal Process,62(3):531–544. doi: 10.1109/TSP.2013.2288675
Hochreiter S,Schmidhuber J. 1997. Long short-term memory[J]. Neural computation,9(8):1735–1780 (in Chinese). doi: 10.1162/neco.1997.9.8.1735
Lorenz E N. 1963. Deterministic nonperiodic flow[J]. Journal of Atmospheric Sciences,20(2):130–141 (in Chinese). doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Moghadam R A,Yaghoubi M. 2015. Interval emotional neural network for prediction of Kp,AE and Dst geomagnetic activity indices[C]//2015 International Congress on Technology. Mashhad,Iran:IEEE:325−331. doi: 10.1109/ICTCK.2015.7582690.
Sutcliffe P R. 1999. The development of a regional geomagnetic daily variation model using neural networks[J]. Annales Geophys,18(1):120–128.
Vastano J A,Kostelich E J. 1986. Comparison of algorithms for determining Lyapunov exponents from experimental data[C]//Dimensions and Entropies in Chaotic Systems. Springer Series in Synergetics,vol 32. Berlin,Heidelberg:Springer:100−107.
Xie H B,He W X,Liu H. 2008. Measuring time series regularity using nonlinear similarity-based sample entropy[J]. Phy Lett A, 372 (48):7140−7146.
Yi S H,Huang S Q,Li X H,Qi W,He Y L,Han S Q,Rong C J,Li Z G. 2010. Modeling and forecasting of the variable geomagnetic field at multiple time scales[C]//IEEE 10th International Conference on Signal Processing Proceedings. Beijing:IEEE:1335−1338. doi: 10.1109/ICOSP.2010.5657017.
-
期刊类型引用(1)
1. 朱悦璐,李光灿,罗冬兰. 统计学与动力学方法结合的渭河上游干旱研究. 水资源与水工程学报. 2024(05): 40-45 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: