Selection and scaling of ground motion records for great scenario earthquakes based on the conditional mean spectrum
-
摘要: 在PEER地震动数据库(PGMD)的基础上, 结合近几年国内外特大地震的地面运动记录, 建立了地面运动数据库, 同时根据日本MW9.0特大地震获得的141组记录进行统计回归建立加速度反应谱衰减关系, 并采用条件均值反应谱法, 即设定地震与结构概率需求结合的方法选择地面运动. 选波实例表明, 当设定地震为特大地震时, 基于条件均值反应谱法选取地面运动记录时, 扩展数据库中大震记录并建立符合大震记录加速度反应谱的衰减关系是十分必要与迫切的. 该思路为进一步研究结构动态时程分析中地面运动记录选取问题及所选记录提供了依据.Abstract: In this paper, PEER ground motion database(PGMD) at the Pacific earthquake engineering research center (PEER) was updated by 141 groups of ground motion records in Japan Tohoku earquake on March 11, 2011, building an attenuation model of acceleration response spectrum of MW9.0, having expanded the limitation of this database. Following the disaggregation results from probabilistic seismic hazard analysis, the scenario earthquake and the conditional mean spectrum (CMS) were set up as the target requirement and the selection, and scaling of ground motions for the great scenario earthquake was addressed finally. The results show that the expanded database could reflect the different selection and scaling of strong motion records in great earthquakes, and the suggested method could be applied to the structural spectrum analysis.
-
引言
随着强震观测技术的发展,强震动时程记录逐步累积,人们可利用概率统计的方法对地震动的强度进行估计,并直接应用于工程结构抗震设计. 地震动是由震源释放出来的地震波引起的地表附近土层的振动,是由各种周期分量按特定比例组成,其频谱组成随场地土壤条件改变,是工程地震与结构抗震之间的桥梁(胡聿贤,2006). 地震动的物理量大多选定为与地震惯性力联系密切的地震动加速度时程. 在结构工程领域,地震对结构破坏能力的大小主要与地震动的幅值、 频谱特性和持时三大特征有关. 如何确定一次地震动强度的指标并用于结构动态时程分析中选取强震记录,一直是结构抗震领域的一个难点,同时也是基于性态抗震设计所需解决的首要问题. 目前来看,只有匹配目标反应谱的选波方法才能同时反映地震动的振幅和频率特征,因而考虑有阻尼的加速度反应谱的谱形匹配为地震动主要依据进行强震记录的选取更为合理. 总之,选择相似地震和地质条件下,实际地震动强度记录的反应谱与目标谱相匹配的时程记录是目前一致认可的选波原则之一. 本文研究现有几种主要的强震动记录的选取方法,扩展了太平洋地震工程研究中心的地面运动数据库(PGMD),同时根据日本MW9.0特大地震记录整理回归建立加速度反应谱衰减关系,并应用匹配条件均值反应谱法选择地震动.
1. 现有选波方法研究
最早关于结构时程分析中选波的规定见1990SEAOC蓝皮书 Structural engineers association of California (SEAOC). 1990. Recommended lateral force requirements and commentary,‘Blue Book’ 5th edn. SEAOC,Sacramento,CA. : “时程分析应至少使用3组相似的水平分量,取其最大参数反应作为设计值”,“应用于场地的地面运动时程应代表实际地震地面运动,其反应谱应近似于场地设计谱”,“通过放缩使其均方根不低于1.3倍的DBE(或MCE),在T1-T1+2.0 s内大于10%”. 1994年的UBC(NEHRP条款) Building Seismic Safety Council. 1994. National earthquake hazards reduction program. Recommended provisions for the development of seismic regulations for new buildings. Washington D D. 规定: 如果用7组或更多记录,设计用其平均值. ATC-40 ATC (Applied Technology Council). 1996. Seismic evaluation and retrofit of concrete buildings,ATC-40. California Seismic Commission,Sacramento,CA. 规定,不小于3组水平分量,选择记录地震: M,R及震源机制相符,场地条件相符,当没有相似记录使用人工合成地面运动. ATC-63 Quantification of building seismic performance factors. April 2008. ATC-63 project report (90% Draft),FEMA P695. 报告基于8点原则,针对中硬场地,建议了22条远场地震波,28条近场地震波,来考虑地震波离散性的影响. 根据美国抗震规范选择时程,结构反应的中值估计可相差3倍(Cornell,2006).
本文所指的目标谱是一种加速度反应谱,代表结构抗震设防需求及工程场地地震境况,包括规范设计谱、 一致概率反应谱及条件均值谱等. 各国抗震规范反应谱均采用理想化数学表达式形式,可由2—3个独立变量确定. 严格说来,任何谱的频谱(或周期)都是无穷多个独立变量,谱中幅值是频率(或周期)的连续函数,每一个频率(或周期)的谱值都是一个独立变量. 假若将谱简化为三直线(或曲线表达式),则表示谱有3个独立变量. 若进一步假定谱形简化为一个或两个变量,ATC-63中在0.1—0.5 s周期内加速度反应谱平均值和1 s周期的反应谱值时就只采用两个独立变量,Housner (1975)采用谱强度概念后就只有一个独立参数. 此时,反应谱与振幅在反映地震动强度上基本等价. 我国抗震规范中设计标准反应谱最长周期仅为6 s,远不能满足某些长周期结构的需要,也无法确定各周期点谱值的概率水平,而且规范中设计谱尚未考虑近断层地震作用的影响(耿淑伟,2005). 将其作为目标谱用于选择地面运动记录,很难准确预测结构在未来可能遭遇地震的真实反应特性.
Cornell(2006)阐明一致概率反应谱(uniform hazard spectrum,简写为UHS)表示不同周期下加速度谱值具有相同概率,是若干个设定地震反应谱的包络线,而非某一个实际未来可能遭遇的地面运动记录的反应谱. 另外,一致概率反应谱与一条真实地震反应谱相比而言太过于广谱,直接作为目标谱用于结构时程分析选择地面运动,其结果将过于保守(王刚,2010).
Baker和Cornell (2005,2006a, b)通过设定震源的震级和震中距等参数,构造满足概率结构需求分析的条件均值反应谱(conditional mean spectrum,简写为CMS). 条件均值反应谱是根据工程场地的设定地震同时考虑结构动力特性,利用加速度反应谱衰减关系确定的加速度反应谱. 条件均值反应谱选波方法基本思路: 基于概率结构需求分析和地震危险性分析建立条件均值反应谱为目标谱,选择与其匹配的地面运动加速度记录用于结构时程分析. 条件概率均值反应谱反映了在不同周期T下反应谱不完全相同的超越概率,即指定周期下反应谱值的超越概率最大而其它周期谱值超越概率介于最大与均值之间(王刚,2010). 大于或者小于均值反应谱的标准方差数值ε如图1所示,根据概率结构需求分析或规定结构加速度反应值Sa(T1)确定ε(T1). 某个给定周期T1的反应谱值具有给定的ε(T1)个标准方差数,其它周期上的ε(Ti)则小于此ε(T1). 由概率地震危险性分析确定震级和震中距等地震参数的特征值,将此特征值代入加速度反应谱衰减关系,确定Sa(Ti)平均值.
2. 地面运动数据库及扩展
PGMD地面运动记录数据库包括了世界范围内位于地质活跃区的浅源地震,其中每条记录都含有各种距离参数、 场地类型及震源参数. 美国抗震安全委员会(BSSC)的“国家减轻地震灾害计划”(NEHRP)最新一版推荐规程将PGMD数据库作为地面运动记录的主要来源. 20世纪90年代,太平洋地震工程研究中心(PEER)迫于改善使用地震地面运动记录的需求,开始搭建强震记录的网络搜索数据库. PEER的新一代衰减关系(next generation attenuation,简写为NGA)数据库共收集整理了来自1 456个地震台的173次地震,共计3 551组三分量地震波加速度时程. 该数据库记录的矩震级分布为M4.27—7.9,震源距分布约为5—558 km,其中M≥8.0大地震地面运动记录一直是空白. 当同时对震级、 距离、 震源机制加以限制并规定每次地震只取1个记录时,仅有9条记录备选.
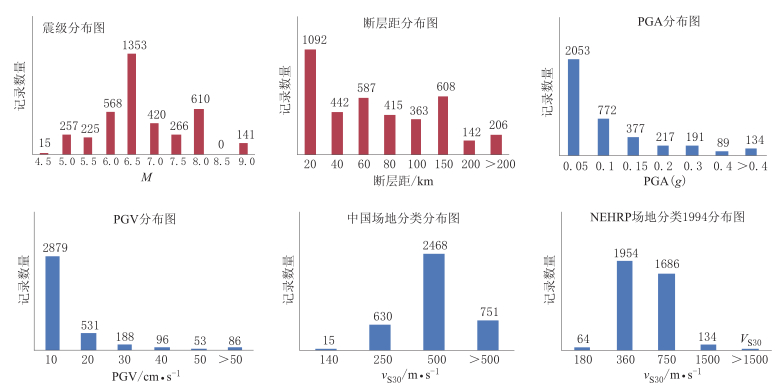
本文在PEER地面运动数据库(PGMD)的基础上整理了近几年国内外特大、 大地震的地面运动记录,建立地面运动数据库. 其中包括: 2011年3月11日日本Tohoku MW9.0地震地面运动记录141组(温瑞智等,2011),2008年5月12日中国汶川MS8.0地震的129组主震记录,以及2010年9月3日新西兰MW7.1地震44组记录,共计314组实际地震地面运动记录. 日本MW9.0地震震中位于38.1°N、 142.9°E,震源深度24 km,台站场地30 m. 等效剪切波速分布为210—2 270 m/s,断层距分布为10—643 km范围内. 中国汶川MS8.0地震,震中位于30.986°N、 103.364°E,震源深度14 km,台站场地30 m. 等效剪 切波速为221—660 m/s,断层距的范围为10—552 km. 新西兰MW7.1地震,震源深度11 km,台站场地30 m. 等效剪切波速为128—760 m/s,断层距的范围为3.6—194 km. 本研究不但对PGMD数据进行了适时的扩展,更重要的是填补了目前PGMD数据库缺失大震记录的空白. 本数据库共3 865组地面运动记录,其参数分布情况见图2.
本研究采用Boore (2008)提出的地面运动记录数据处理方法及TSPP程序进行滤波等处理记录,使用记录频率段为0.1—25 Hz,阻尼比为5%的弹性加速度反应谱. 数据库中的所有地面运动记录都旋转成平行与垂直断层方向的两个水平分量. 本文采用两个水平方 向加速度反应谱的几何平均值作为计算选取记录的依据. K-NET数据台站分布情况见图3.
3. NGA衰减关系的适用性
衰减关系是在大量记录统计回归分析后得到的地震动预测方程. 美国NGA 研究计划对全美的断层特性、 场地特性等进行大量研究,研究项目组用获得的5种浅层活跃地震动衰减模型来构造确定性的境况地震(Abrahamson,Silva,2008; Boore,Atkinson,2008; Campbell,Bozorgnia,2008; Chiou,Youngs,2008; Idriss,2008),建立不同地区不同设防水准对应的地面运动目标反应谱. 加速度反应谱的衰减关系是建立目标反应谱的前提. 5组回归模型所用数据量不同,AS08和CY08包括余震记录,所以数据量较大; I08也考虑余震记录,但仅限于基岩场地记录; AS08,CB08和CY08考虑断层的上盘效应、 断层深度. 5组模型地震参数各不相同,震源因素包括矩震级和震源机制,但I08没有区分走滑与正断层地震. AS08,CB08和CY08用地面到破裂顶的深度来考虑破裂深度效应. 在距离上,BA08用台站到破裂面投影的最短水平距离Rjb,其它4个用台站到破裂面最短距离Rrup. NGA采用全球范围内的构造浅层地震,用于美国西部场地的地震动预测,对于国内的数据库建立和地面运动记录选取有实际意义. 目前,国内各类规范中的衰减关系仅适用于基岩场地.
PEER的新一代衰减关系(NGA)主要适用范围如下: 走滑地震M<8.5,逆断层地震M<8.0; 断层距小于200 km,距地表30 m的土层剪切波速为180—1 300 m/s,加速度谱周期为0.01—10 s. 由于篇幅所限,本文选择其中两个衰减关系由M7.6外推至M9.0,采用日本M9.0记录验证其适用性. 其中,Boore和Atkinson(2008)则建议采用公式(1)中模型进行地震动参数的衰减分析(以下简称BA08衰减关系).

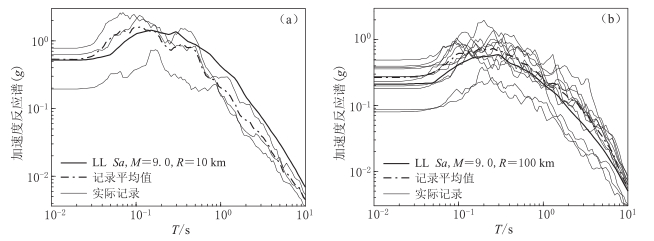
式中,lnY为地震动参数值,即峰值加速度和结构自振周期为0.04—10 s内的加速度反应谱值,采用两水平分量的几何平均值; M为震级; Rjb为断层距; vS30为距地表30 m土层平均剪切波速. 假定地震为本次M9.0地震,震源机制为逆断层地震,两个场地的断层距分别为10和200 km,场地地下30 m剪切波速均为760 m/s. 由公式(1) BA08衰减关系预测的加速度反应谱结果如图4所示. 可见BA08衰减关系外推至M9.0地震时,当断层距较小,即近场地震,短周期的加速度反应谱的预测值偏小而长周期预测值偏大; 当断层距较大,即中远震,短周期的加速度反应谱的预测值偏大而长周期预测相对更接近实际情况下的均值.
Campbell和Bozorgnia (2008)采用以下衰减关系模型(以下简称CB08衰减关系),见公式(2). CB08衰减关系除了考虑震级、 断层距、 震源机制、 场地条件外,还考虑了上盘效应的影响.

式中,fi表示震级M,断层距R,断裂类型F,上盘效应HW,浅层场地条件S,沉积或盆地深度D对地面运动的影响函数. 设定地震与实际记录谱选择方法同上,比较 CB08衰减关系得到的预测谱值和实际记录谱值. 即当设定地震震级M=9.0、 断层距为10 km时,实际记录及其平均值和预测值见图5a; 设定断层距为200 km时见图5b. 可见CB08衰减关系外推至M9.0地震时,当断层距较小,即近场地震,其结果与BA08衰减关系相近,短周期的加速度反应谱的预测值偏小于实际记录谱的平均值而长周期预测值偏大; 当断层距较大,即中远震,预测值整体偏大,长周期处偏离较为突出且远大于实际谱值.
以上分析表明,利用现有衰减关系预测M9.0地震加速度反应谱与实际记录加速度反应谱差距较大,特别在大震近场情况下两者谱形相差明显. 可见现有衰减关系并不可以外推应用于M9.0地震,也不能直接用其建立目标反应谱.
4. 基于条件均值谱的选波方法及实例分析
本文仅考虑断层距和场地条件因素建立衰减关系,模型见公式(3). 利用本次M9.0地震获得141组两个水平方向的实际记录及其地震动相关参数,采用高斯-牛顿非线性最小二乘,拟合衰减关系模型的回归系数. 数据分布: 断层距从10—635 km,场地地下30 m平均剪切波速从210—2 270 m/s,地面运动记录峰值加速度PGA从0.001g—1.904 8g. 参考BA08加速度反应谱衰减关系,确定回归模型为式(3)(以下简称LL衰减关系).

统计回归得到不同周期的回归系数(表1). 本衰减关系反映了不同周期加速度反应谱值关于断层距、 场地条件的衰减关系,可用其对M9.0逆断层地震的加速度反应谱进行预测(图6). 由于记录数量有限,未对其剪切波速进行限制,其中图6a,b分别为设定VS30=760 m/s情况下,R=10和100 km时,应用公式(3)得到的预测加速度反应谱与相应条件的实际记录谱值. 可见,LL谱加速度衰减关系可以很好地拟合M9.0地震的加速度反应谱,可将其作为建立条件概率均值谱的依据.
表 1 LL衰减关系回归系数Table 1. Regression coefficient of LL attenuation model of acceleration response spectrum
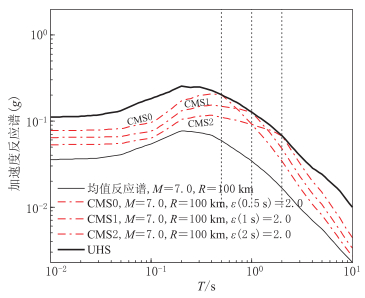
本文采取公式(3)LL衰减关系代替PGMD系统中NGA的衰减关系,建立M9.0地震的条件均值反应谱为目标谱. 为验证增加大震记录及调整衰减关系的必要性,本文例举如下算例: ① 若某场地经概率地震危险性分析分布式结果显示设定地震M9.0、 断层距为R=100 km的地震发生概率凸显,场地地下30 m平均剪切波速为760 m/s,拟建结构自振周期为T1=1 s,假定根据所需结构加速度谱Sa(T1)值确定谱形参数ε=2.0; ② 若场地的断层距为R=10 km,其它条件同①,确定目标反应谱,当设计地震为M9.0,断层距为R=100 km,以指定周期为2 s的加速度反应谱值的ε=2.0为已知,生成条件均值反应谱(CMS)如图7a所示. 当设计地震为MW9.0,断层距为R=10 km,谱形参数ε=2.0时,其条件均值反应谱为图7b所示.
本文使用匹配条件均值谱的均值和方差的理论及算法(Jayaram et al,2011). 以上述情况为例,将图7中条件均值谱作为目标谱,采用蒙特卡罗概率方法匹配目标谱的均值和方法,从补充大震记录后的扩展数据库中,选择10组地面运动记录匹配目标谱,选择结果及放缩系数见表 2. 按照记录放缩后与目标谱优先匹配程度,即两者均方差逐渐增大的顺序进行排序. 由表 2谱形匹配结果可见,在选择的10组记录中有3组记录震级M=9.0,且放缩系数分别为1.01,2.78和1.44,两者相关性见图8a. 表明对震级M=9.0记录的调幅较小,采用此记录能更多地反映实际大震特征. 图8b,c所示分别为放缩系数和断层距及场地剪切波速的关系. 由图8d,e和f可知,记录的放缩系数(SF)与PGA,PGV和PGD都存在很好的相关性. 其中SF与PGA的决定系数R2为0.736,说明统计回归的趋势线与原数据拟合程度较好,即PGA的对数与SF存在线性相关性. 当M<8.0时,SF与PGV的决定系数R2为0.567; 当M=9.0时,SF与PGV的决定系数R2为0.999; 而不考虑震级影响时,两者的决定系数接近于零. SF与PGD的决定系数R2为0.911,即PGD的对数与SF存在显著线性相关性. 确定选波原则时,可考虑限定PGA,PGV和PGD的最小值而间接限制放缩系数的最大值. 但由于数据有限,不建议将回归公式直接用于记录的选取. 由此例可见,近场大震记录对于数据库在选波系统中的应用十分重要.
表 2 扩展数据库选波结果Table 2. The results of PGMD expanded 9.0 magnitude ground motion records
![]() 图 8 选波结果中的放缩系数与地震动参数的相关性分析(a) 震级-放缩系数; (b) 断层距-放缩系数; (c) 剪切波速-放缩系数; (d) PGA-放缩系数; (e) PGV-放缩系数; (f) PGD-放缩系数Figure 8. Logarithmic linear correlation between scalar factors and earthquake intensity parameters(a) Earthquake magnitude-scalar factor; (b) Fault distance-scalar factor; (c) vS30-scalar factor; (d) PGA-scalar factor; (e) PGV-scalar factor; (f) PGD-scalar factor
图 8 选波结果中的放缩系数与地震动参数的相关性分析(a) 震级-放缩系数; (b) 断层距-放缩系数; (c) 剪切波速-放缩系数; (d) PGA-放缩系数; (e) PGV-放缩系数; (f) PGD-放缩系数Figure 8. Logarithmic linear correlation between scalar factors and earthquake intensity parameters(a) Earthquake magnitude-scalar factor; (b) Fault distance-scalar factor; (c) vS30-scalar factor; (d) PGA-scalar factor; (e) PGV-scalar factor; (f) PGD-scalar factor5. 讨论与结论
在结构时程分析中地面运动记录的不确定性是导致结构反应参数离散性过大的主要原因之一. 本文在PEER地面运动数据库(PGMD)的框架及数据模式的基础上,结合近几年国内外特大地震地面运动记录建立地面运动数据库,同时根据日本MW9.0特大地震记录整理回归建立加速度反应谱衰减关系,并应用匹配条件均值反应谱法选择地面运动. 选波实例表明,当设定地震为特大地震时,基于条件均值反应谱法选取地面运动记录时,扩展数据库中大震记录并建立符合大震记录加速度反应谱的衰减关系是十分必要与迫切的.
鉴于文中表2所列的选波结果,在保证谱形匹配的前提下,限制震级大于MW6.0、 放缩系数小于5,可得到7条地面运动记录. 在此基础上增加限制条件PGA大于0.3g,则可得3条地面运动记录用于结构时程分析. 因此,建议使用谱形匹配选波时,可将震级、 放缩系数、 PGA列入选波限制条件,优化选波结果.
本研究实例为坚硬土层场地的大震,对于此类情况,建议使用震级大于MW6.0、 放缩 系数小于5,PGA大于0.3g作为限制条件,在此基础上匹配条件均值反应谱. 对于M5.0 —7.0设定地震选波原则可参考ATC-63报告. 基于8点原则,按照《抗震规范》规定最大地震影响系数,确定与Sa(T1)的比值进而确定ε值,生成条件均值反应谱作为目标谱,匹配目标谱.
下一步研究的问题,即通过结构时程分析结果评价条件均值谱法及其它选波方法,为抗震规范结构时程分析选取地面运动记录提供科学依据及参考.
-
图 8 选波结果中的放缩系数与地震动参数的相关性分析
(a) 震级-放缩系数; (b) 断层距-放缩系数; (c) 剪切波速-放缩系数; (d) PGA-放缩系数; (e) PGV-放缩系数; (f) PGD-放缩系数
Figure 8. Logarithmic linear correlation between scalar factors and earthquake intensity parameters
(a) Earthquake magnitude-scalar factor; (b) Fault distance-scalar factor; (c) vS30-scalar factor; (d) PGA-scalar factor; (e) PGV-scalar factor; (f) PGD-scalar factor
表 1 LL衰减关系回归系数
Table 1 Regression coefficient of LL attenuation model of acceleration response spectrum

表 2 扩展数据库选波结果
Table 2 The results of PGMD expanded 9.0 magnitude ground motion records

-
耿淑伟. 2005. 抗震设计规范中地震作用的规定[D]. 哈尔滨: 中国地震局工程力学研究所: 3-9. 胡聿贤. 2006. 地震工程学[M]. 北京: 地震出版社: 133-134. 王刚. 2010. 地震波选择方法, 工具, 及其在基于性能的抗震设计中的应用[C]//第四届粤港澳地震科技研讨会. 香港: 香港天文台: 9. 温瑞智, 周宝峰, 史大成, 任叶飞. 2011. 日本MW9.0地面运动观测与记录初步分析[J]. 国际地震动态, (4): 16-21. Abrahamson N A, Silva W J. 2008. Summary of the Abrahamson & Silva NGA groundmotion relations[J]. Earthq Spectra, 24(1): 67-97.
Baker J W, Cornell C A. 2005. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon[J]. Earthq Eng Struct D, 34(10): 1193-1217.
Baker J W, Cornell C A. 2006a. Spectral shape, epsilon and record selection[J]. Earthq Eng Struct D, 35(9): 1077-1095.
Baker J W, Cornell C A. 2006b. Correlation of response spectral values for multi-component ground motions[J]. Bull Seism Soc Amer, 96(1): 215-227.
Boore D. 2008. TSPP-A Collection of FORTRAN Programs for Processing and Manipulating Time Series[R]. U S Geological Survey Open-File Report.
Boore D M, Atkinson G M. 2008. Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5% damped PSA at spectral periods between 0.01 s and 10.0 s[J]. Earthq Spectra, 24(1): 99-138.
Campbell K W, Bozorgnia Y. 2008. NGA ground motion model for the geometric mean horizontal component of PGA, PGV, PGD, and 5% damped linear elastic response spectra for periods ranging from 0.01s to 10.0 s[J]. Earthq Spectra, 24(1): 139-171.
Chiou B S J, Youngs R R. 2008. Chiou-Youngs NGA ground motion relations for the geometric mean horizontal component of peak and spectral ground motion parameters[J]. Earthq Spectra, 24(1): 173-215.
Cornell C A. 2006. Should uniform hazard spectra be used for design? How should design response spectra be determined considering uniform hazard spectra from design maps and hazard deaggregation data?[R]. Proceedings of the Third ATC-35/USGS National Earthquake Ground Motion Mapping Workshop. San Mateo, December 7-8.
Housner G W. 1975. Measure of Severity of Earthquake Ground Shaking[R]. 2nd US NCEE. Ann Arbor, Michgan.
Idriss I M. 2008. An NGA empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes[J]. Earthq Spectra, 24(1): 217-242.
Jayaram N, Lin T, Baker J W. 2011. A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance[J]. Earthq Spectra, 27(3): 797-815.
-
期刊类型引用(17)
1. 何乡,吴子燕,贾大卫. 联合极限状态下基于最大熵可靠度的易损性分析. 计算力学学报. 2022(01): 21-27 .  百度学术
百度学术
2. 王晓磊,吕大刚,阎卫东. 考虑竖向地震动影响的某核电安全壳地震易损性研究. 原子能科学技术. 2022(06): 1060-1068 .  百度学术
百度学术
3. 王珊,郝明辉,张郁山,赵凤新. 基于小波函数的地震动反应谱与峰值位移拟合方法. 地震学报. 2021(03): 376-386+260 .  本站查看
本站查看
4. 贾大卫,吴子燕,何乡. 基于概率-非概率混合可靠性模型的结构地震易损性分析. 地震工程与工程振动. 2021(04): 90-99 .  百度学术
百度学术
5. 贾大卫,吴子燕,王其昂. 考虑结构极限状态随机性的多维易损性分析. 自然灾害学报. 2020(01): 89-100 .  百度学术
百度学术
6. 贾大卫,吴子燕,王其昂. 基于显示连通贝叶斯网络的机场塔台地震易损性分析. 计算力学学报. 2020(01): 14-19 .  百度学术
百度学术
7. 侯红梅,刘文锋. 综合考虑场地特征周期和结构基本周期影响的地震动选择方法研究. 工程抗震与加固改造. 2020(01): 146-153+145 .  百度学术
百度学术
8. 贾大卫,吴子燕,何乡. 基于凸集模型的结构地震多维易损性分析. 计算力学学报. 2020(06): 763-769 .  百度学术
百度学术
9. 张锐,李宏男,王东升,成虎. 结构时程分析中强震记录选取研究综述. 工程力学. 2019(02): 1-16 .  百度学术
百度学术
10. 温瑞智,冀昆,任叶飞. 结构时程分析中多层次强震动记录输入选取研究综述. 地震工程与工程振动. 2019(05): 1-18 .  百度学术
百度学术
11. 吕大刚,刘亭亭,李思雨,于晓辉. 目标谱与调幅方法对地震动选择的影响分析. 地震工程与工程振动. 2018(04): 21-28 .  百度学术
百度学术
12. 张锐,成虎,吴浩,王东升. 时程分析考虑高阶振型影响的多频段地震波选择方法研究. 工程力学. 2018(06): 162-172 .  百度学术
百度学术
13. 吕大刚,周洲,王丛,于晓辉. 考虑巨震的四级地震设防水平一致风险导向定义与决策分析. 土木工程学报. 2018(11): 41-52 .  百度学术
百度学术
14. 王珊,张郁山. 各类抗震设计规范对设计地震动时程规定的对比分析. 中国地震. 2017(01): 56-67 .  百度学术
百度学术
15. 朱瑞广,于晓辉,吕大刚. 基于地震动模拟的一致危险谱和条件均值谱生成及应用. 工程力学. 2015(S1): 196-201 .  百度学术
百度学术
16. 张云,谭平,郑建勋,周福霖. 梁桥结构地震反应分析中输入地震动选取及调整方法研究. 振动与冲击. 2015(06): 18-23 .  百度学术
百度学术
17. 张思慧,赵刚,张恒璟,黄声和. 北京房山站神经网络高程时间序列分析. 地球物理学进展. 2014(03): 1084-1089 .  百度学术
百度学术
其他类型引用(15)




 下载:
下载: