Effect of cross-section-shape randomness of underground inclusion on scattering of plane SH waves
-
摘要: 采用波函数展开法及边界离散的方法给出了任意断面形状的地下夹塞对平面SH波散射的半解析解; 利用蒙特卡罗方法随机模拟产生了30组夹塞断面样本， 通过对该样本在平面SH波入射下地表位移幅值的统计分析， 研究了夹塞断面形状随机性对平面SH波散射的影响. 结果表明， 夹塞断面形状随机性对平面SH波的散射具有重要影响. 以圆形夹塞为例， 当断面半径的变异系数为0.1时， 地表位移响应幅值变异系数可达0.71. 随着入射频率的升高， 变异系数逐渐增大； 随着夹塞刚度的降低， 变异系数逐渐增大； 随着夹塞埋深的增加， 变异系数逐渐减小.Abstract: The semi-analytical solution of scattering of plane SH waves by underground inclusion with arbitrary cross-section in half-space is presented using wave functions expansion method combined with boundary discrete method. Monte Carlo method is used to randomly generate 30 samples for cross-section shape of the inclusion, and the effect of cross-section-shape randomness on scattering of plane SH waves are studied by statistical analysis of the surface displacement amplitudes. It is shown that, cross-section-shape randomness has significant effect on the scattering of SH waves around an inclusion in half-space. When the variation coefficient of inclusion radius is equal to 0.1, for an inclusion of circular shape, the variation coefficient of surface displacement amplitude may be up to 0.71. The variation coefficient increases as the incident frequency increases. The variation coefficient increases as the inclusion rigidity decreases. The variation coefficient decreases as the inclusion depth increases.
-
引言
地表附近的局部夹塞对地震动的影响一直是地震工程中比较引人关注的课题之一． Pao和Mow(1973)采用波函数展开法开创性地给出了全空间中圆形夹塞对平面波散射的解析解． Dravinski(1983)采用边界积分法研究了半空间中多个夹塞对弹性波的放大作用． Wong等(1985)采用杂交有限元和特征函数展开法研究了半空间中椭圆夹塞对平面波的散射． 袁晓铭(1996)采用波函数展开法给出了半空间中圆形夹塞对SH波散射的解析解，对全空间解(Pao，Mow，1973)进行了拓展． Manoogian和Lee(1996)采用波函数展开法结合加权残值法给出了半空间中任意形状截面夹塞对SH波散射的解． 刘殿魁和田家勇(1999)采用格林函数法求解全空间中界面圆形弹性夹杂对SH波的散射． 袁晓铭和孙锐(2000)分析了饱和砂土透镜体(夹塞)液化对建筑物地震反应的影响． 梁建文等(2009a，b)和张炳政等(2010)采用有限元法结合人工边界研究了透镜体(椭圆形夹塞)对地震动的线性和非线性放大作用． 刘中宪等(2012)采用间接边界积分方程法求解了饱和半空间中夹塞对平面波的散射．
值得指出的是，上述研究均针对确定性夹塞形状. 考虑到夹塞实际形状与计算形状之间存在一定出入，研究夹塞断面随机性对波散射的影响对工程场地地震安全性评价具有重要参考价值. 但就作者所知，该问题目前还鲜有研究．
本文首先采用波函数展开法及边界离散的方法给出了任意断面形状的地下夹塞对平面SH波散射的半解析解； 然后以圆形夹塞为例，采用蒙特卡罗方法随机模拟产生了30组夹塞断面样本. 通过对该样本在平面SH波入射下地表位移响应的统计分析，研究了夹塞断面形状随机性对平面SH波散射的影响，得出了一些对工程场地地震安全性评价具有参考价值的结论．
1. 方法
图 1所示为弹性、 均匀和各向同性半空间中一埋深为D、 区域为Ω的任意形状夹塞． 半空间介质剪切模量为G1，剪切波速为v1； 夹塞区介质剪切模量为G2，剪切波速为v2． 一频率为ω的平面SH波以角度γ入射． 以半空间地表为对称面，构造夹塞区的镜像，则上述半空间问题转化为全空间波动问题(袁晓铭，1996)．
半空间中的总位移场可写为
式中： w1i表示入射波; w2i表示反射波；w1Γ，w2Γ分别表示夹塞区及其镜像产生的散射波； wj表示夹塞区内部位移场. 则在坐标系r1o1θ1中可分别表示如下(时间因子exp(iωt)略去)：
式中: k1=ω/v1为半空间中剪切波波数； k2=ω/v2为夹塞中剪切波波数； γ为SH波的入射角度； Hn(x)(2)表示第二类汉克尔函数； Jn(x)表示贝塞尔函数； Pjn=Hn+j(2)(2kD)+(-1)jHn-j(2)(2kD)，Qjn=Hn+j(2)(2kD)-(-1)jHn-j(2)(2kD)，其中j与n取值为0，1，2，…； ε0=1，εj=2(j≥1)； An，Bn，Cn，Dn为待定系数，可由夹塞与半空间交界面位移和法向剪应力连续的边界条件求得．
将边界离散为M个点(Moeen-Vaziri，Trifunac，1988)，离散每一点的位移和法向剪应力均应满足下式：
其中
式中β为边界点法向与径向的夹角．
对于任意形状边界，采用Moeen-Vaziri和Trifunac(1988)的方法将边界离散成足够密集的离散点，将相邻两点间连线的垂直方向作为曲线在该点的法向量来计算其夹角β. 只要控制好相邻两点的距离使其足够小，即可满足精度要求．
设A和B为边界上相邻的两点，将A(ra，θa)和B(rb，θb)两点连线的垂线作为A点处边界线的法向量n，则夹角β可表示为
将式(2)—(6)代入式(7)的位移边界条件，将式(8)—(12)代入式(7)的应力边界条件，可得到如下线性方程组：
式中： S为2M×4N的系数矩阵，由散射场及夹塞内位移场决定，其中M为夹塞边界离散点的个数，N为级数的截断项数； R为2M×1的列向量，由自由场决定； X=[A1，A2，…，AN，B1，B2，…，BN，C1，C2，…，CN，D1，D2，…，DN]T为待定系数列向量. 该超定方程组可以采用最小二乘法求解． 只要求出待定系数，就可以得到地表位移．
2. 数值结果与分析
以圆形夹塞为例，采用蒙特卡罗方法(Shinozuka，Deodatis，1991)随机产生30组以矢径为变量的夹塞截面样本，每组样本12个矢径，均服从均值为1、 标准差为0.1 的正态分布． 用三次样条函数将每组样本矢径端点连接起来，便构成夹塞截面形状． 图 2给出了30个截面形状样本，每个小图示意5个样本．
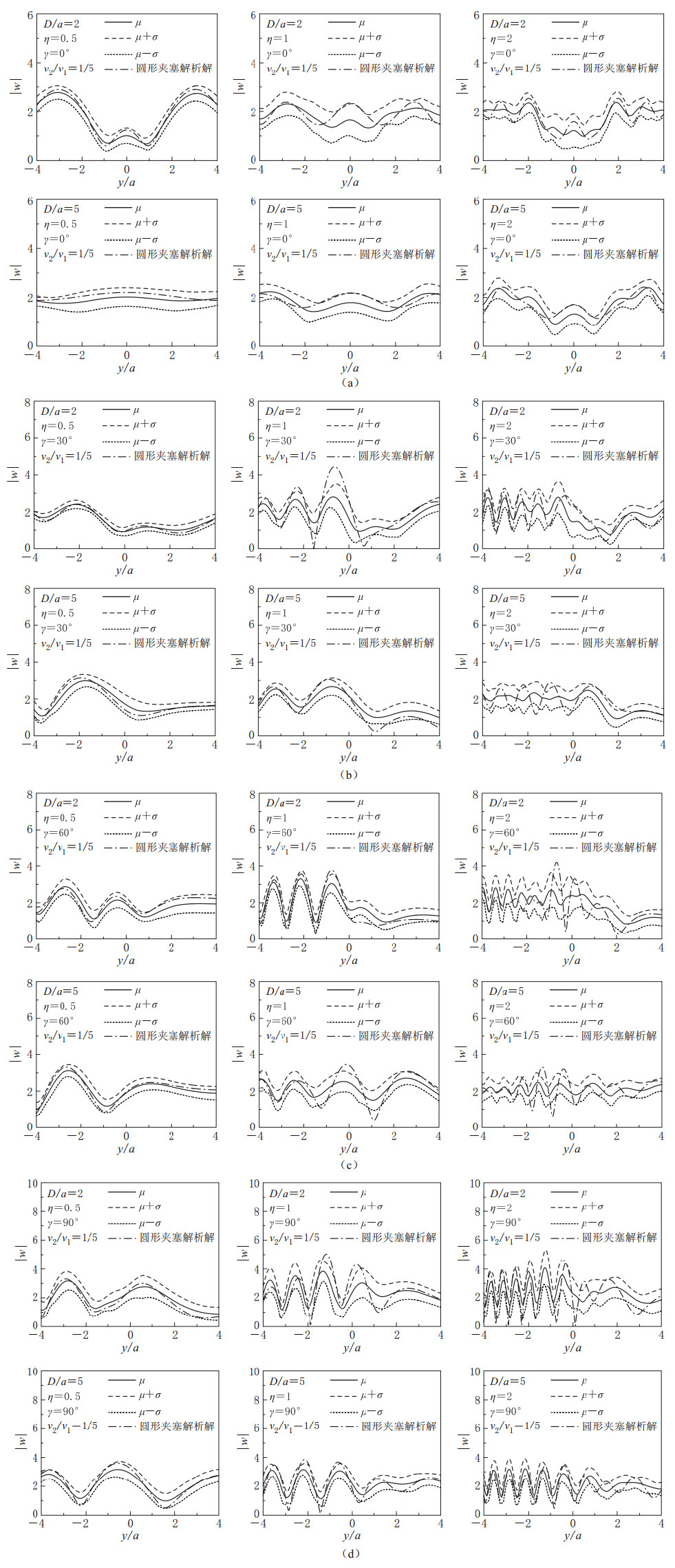
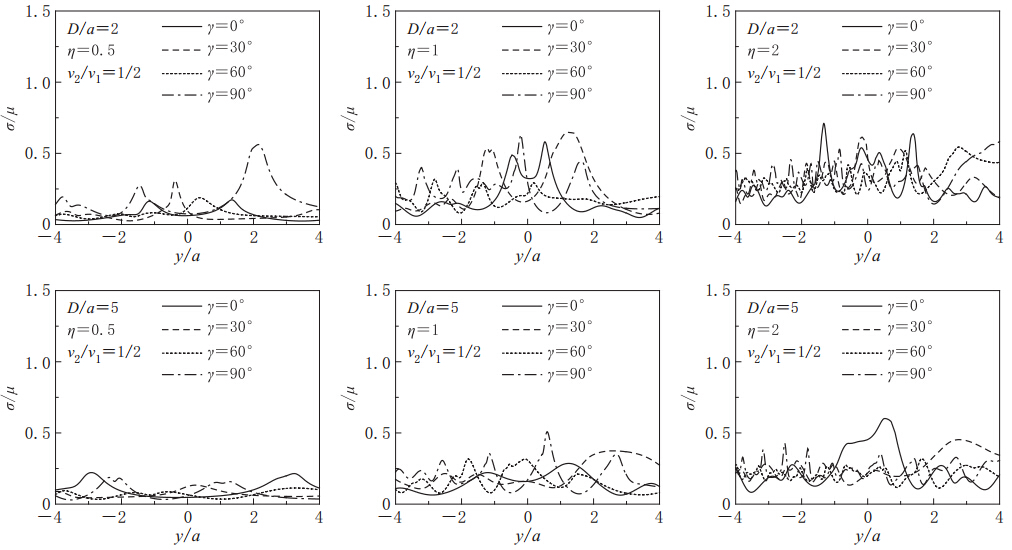
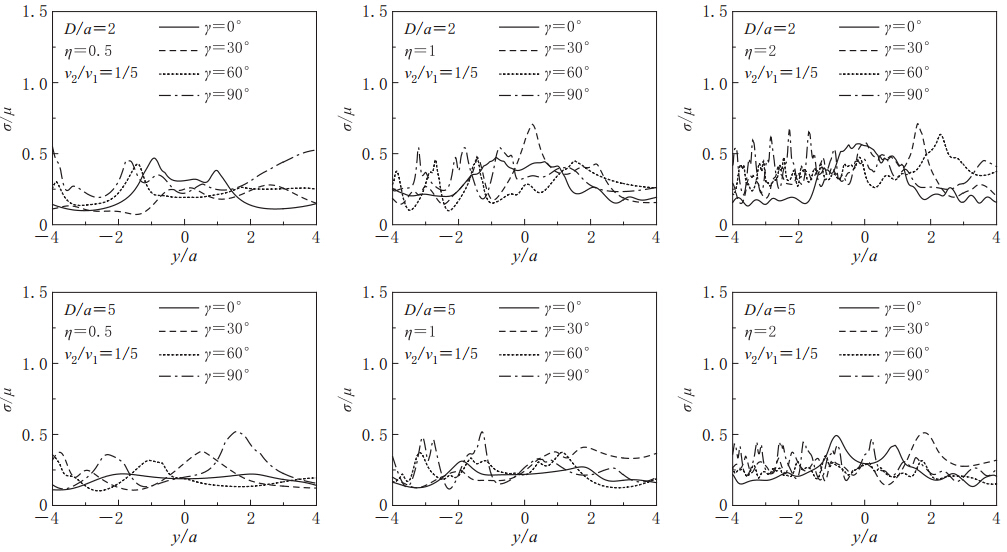
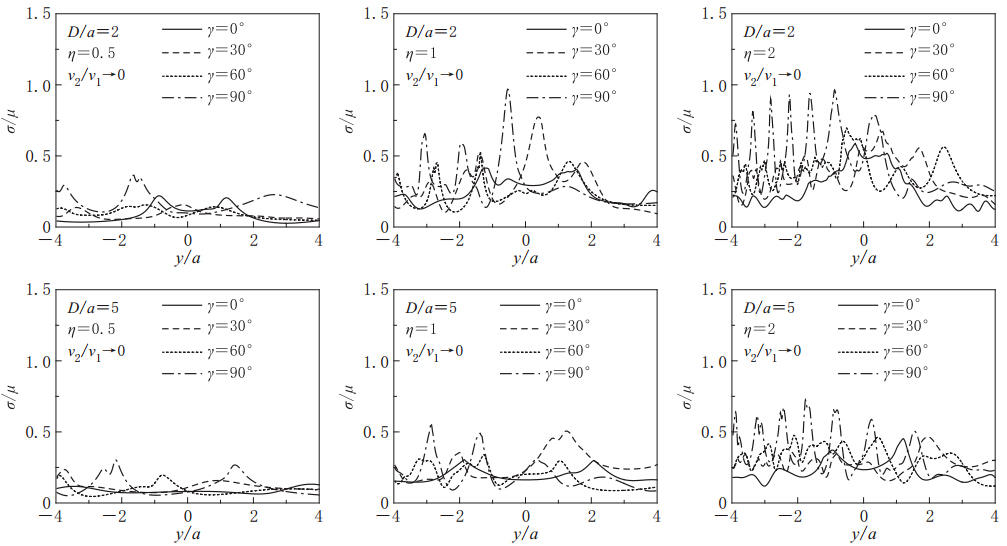
定义夹塞直径均值2a与入射波波长λ之比为入射波的无量纲频率η=2a/λ=ωa/πv1． 分别求解此30组不同截面夹塞在平面SH波入射下地表位移的动力响应，并求得30组地表位移响应幅值的均值μ、 标准差σ和变异系数σ/μ． 图 3和图 4分别给出了夹塞区与半空间介质剪切波速比v2/v1=1/2和1/5时μ和μ±σ的值，同时为了便于比较，图中也给出了圆形夹塞的解析解(袁晓铭，1996)． 图 5和图 6则分别给出了夹塞区与半空间介质剪切波速比v2/v1=1/2和1/5时地表位移响应幅值的变异系数σ/μ． 图中计算参数： 埋深D/a=2和5；密度比ρ2/ρ1=2/3； 无量纲频率η=0.5，1和2； 入射角γ=0°，30°，60°和90°． 横坐标y/a表示地表观察点距夹塞中心的水平距离，纵坐标|w|表示地表位移响应幅值． 为了便于比较分析，图 7给出了夹塞刚度趋于无穷小极限情况(洞室)时，地表位移响应幅值的变异系数σ/μ．
![]()
图 3 30组任意形状夹塞的地表响应位移幅值均值和标准差(ρ2/ρ1=2/3, v2/v1=1/2)(a) γ=0°; (b) γ=30°Figure 3. Mean value and standard deviation of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/2)(a) γ=0°; (b) γ=30°![]()
图 4 30组任意形状夹塞的地表响应位移幅值均值和标准差(ρ2/ρ1=2/3, v2/v1=1/5)(a) γ=0°; (b) γ=30°Figure 4. Mean value and standard deviation of surface displacement amplitude for30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/5)(a) γ=0°; (b) γ=30°![]()
图 5 30组样本断面夹塞地表位移响应幅值的变异系数(ρ2/ρ1=2/3, v2/v1=1/2)Figure 5. Variation coefficient of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/2)![]()
图 6 30组样本断面夹塞地表位移响应幅值的变异系数(ρ2/ρ1=2/3, v2/v1=1/5)Figure 6. Variation coefficient of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/5)![]()
图 7 30组样本断面夹塞地表位移响应幅值的变异系数(ρ2/ρ1=2/3, v2/v1→0)Figure 7. Variation coefficient of surface displacement amplitude for30 inclusion samples (ρ2/ρ1=2/3,v2/v1→0)从图 3和图 4可以看出，当入射频率较低时，均值与圆形夹塞的解析解非常接近，说明本文结果的可靠性； 而当入射频率较高时，均值与圆形夹塞的解析解差别有所增大，说明当入射频率较高时需要更多的样本．
从图 5和图 6可以看出，夹塞断面形状随机性对平面SH波的散射具有重要影响： 夹塞断面半径的变异系数为0.1时，在v2/v1=1/2情况下，地表位移响应幅值变异系数可达0.65(D/a=2，η=1，γ=30°)和0.71(D/a=2，η=2，γ=0°)； 在v2/v1=1/5情况下，地表位移响应幅值变异系数可达0.71(D/a=2，η=1和2，γ=30°)； 但均小于在v2/v1→0情况(洞室)下的地表位移响应幅值变异系数0.97(D/a=2，η=1，γ=90°)和0.96(D/a=2，η=2，γ=90°)(图 7)． 无论变异系数大小还是峰值出现的位置，均体现了夹塞存在滤波和屏障的双重作用(袁晓铭，1996).值得指出的是，洞室仅存在单一屏障作用，这也是夹塞与洞室存在明显差别的原因．
从图 5和图 6中还可以看出，当入射频率较低时，变异系数比较小； 而随着频率的升高，变异系数逐渐增大． 说明夹塞边界随机变化对高频波影响更大，或者说夹塞断面形状变化对高频波影响更大. 这符合工程波动的基本规律．
比较图 5、 图 6和图 7可以看出，当夹塞与半空间之间刚度差别比较小时，变异系数比较小； 随着夹塞与半空间之间刚度差别逐渐增大，变异系数逐渐增大. 这也符合工程波动的基本规律． 当夹塞埋深较浅时，变异系数较大； 随着埋深增加，变异系数逐渐减小．
3. 结论
本文采用蒙特卡罗方法研究了地下夹塞断面形状随机性对平面SH波散射的影响. 通过数值分析表明，夹塞断面形状随机性对波的散射具有重要影响． 当夹塞断面半径的变异系数为0.1时，地表位移响应幅值变异系数可达0.71． 当入射频率较低时，变异系数较小； 随着频率的升高，变异系数逐渐增大． 当夹塞与半空间之间刚度差别比较小时，变异系数较小； 随着夹塞与半空间之间刚度差别逐渐增大，变异系数逐渐增大． 当夹塞埋深较浅时，变异系数较大； 随着埋深增加，变异系数逐渐减小．
-
![]()
图 3 30组任意形状夹塞的地表响应位移幅值均值和标准差(ρ2/ρ1=2/3, v2/v1=1/2)
(a) γ=0°; (b) γ=30°
Figure 3. Mean value and standard deviation of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/2)
(a) γ=0°; (b) γ=30°
![]()
图 4 30组任意形状夹塞的地表响应位移幅值均值和标准差(ρ2/ρ1=2/3, v2/v1=1/5)
(a) γ=0°; (b) γ=30°
Figure 4. Mean value and standard deviation of surface displacement amplitude for30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/5)
(a) γ=0°; (b) γ=30°
![]()
图 5 30组样本断面夹塞地表位移响应幅值的变异系数(ρ2/ρ1=2/3, v2/v1=1/2)
Figure 5. Variation coefficient of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/2)
![]()
图 6 30组样本断面夹塞地表位移响应幅值的变异系数(ρ2/ρ1=2/3, v2/v1=1/5)
Figure 6. Variation coefficient of surface displacement amplitude for 30 inclusionsamples (ρ2/ρ1=2/3,v2/v1=1/5)
-
梁建文, 张炳政, 巴振宁. 2009a. 层状场地中透镜体对地震动影响的基本规律[J]. 地震工程与工程振动, 29(5): 1-12. Liang J W, Zhang B Z, Ba Z N. 2009a. On the effect of a lenticle in a layered site on ground motion[J]. Journal of Earthquake Engineering and Engineering Vibration, 29(5): 1-12 (in Chinese).
梁建文, 张炳政, 巴振宁. 2009b. 基岩上均匀场地中透镜体对地震动的非线性放大作用[J]. 地震工程与工程振动, 29(6): 13-24. Liang J W, Zhang B Z, Ba Z N. 2009b. Nonlinear amplification of ground motion by a lenticle in single layer on bedrock[J]. Journal of Earthquake Engineering and Engineering Vibration, 29(6): 13-24 (in Chinese).
刘殿魁, 田家勇. 1999. SH波对界面圆柱形弹性夹杂散射及动应力集中[J]. 爆炸与冲击, 19(2): 115-123. Liu D K, Tian J Y. 1999. Scattering and dynamic stress concentration of SH-wave by interface cylindrical elastic inclusion[J]. Explosion and Shock Waves, 19(2): 115-123 (in Chinese).
刘中宪, 梁建文, 李帆. 2012. 流体饱和半空间中夹塞物对平面SV波的散射[J]. 力学季刊, 33(2): 256-268. Liu Z X, Liang J W, Li F. 2012. Diffraction of plane SV waves by an inclusion in saturated poroelastic half-space[J]. Chinese Quarterly of Mechanics, 33(2): 256-268 (in Chinese).
袁晓铭. 1996. 地表下圆形夹塞区出平面散射对地面运动的影响[J]. 地球物理学报, 39(3): 373-381. Yuan X M. 1996. Effect of a circular underground inclusion on surface motion under incident plane SH waves[J]. Acta Geophysica Sinica, 39(3): 373-381 (in Chinese).
袁晓铭, 孙锐. 2000. 饱和砂土透镜体液化对建筑物地震反应的影响[J]. 地震工程与工程振动, 20(1): 68-74. Yuan X M, Sun R. 2000. Effect of liquefaction of lenticular saturated sand zone on seismic response of buildings[J]. Journal of Earthquake Engineering and Engineering Vibration, 20(1): 68-74 (in Chinese).
张炳政, 梁建文, 巴振宁. 2010. 基岩上均匀场地中透镜体对地震动的影响[J]. 天津大学学报, 43(9): 783-791. Zhang B Z, Liang J W, Ba Z N. 2010. Effects of lenticle in single layer on bedrock on ground motion[J]. Journal of Tianjin University, 43(9): 783-791 (in Chinese).
Dravinski M. 1983. Ground motion amplification due to elastic inclusion in a half-space[J]. Earthquake Engng Struct Dyn, 11(3): 313-335.
Manoogian M E, Lee V W. 1996. Diffraction of SH-waves by subsurface inclusions of arbitrary shape[J]. J Eng Mech, ASCE, 122(2): 123-129.
Moeen-Vaziri N, Trifunac M D. 1988. Scattering and diffraction of plane SH-waves by two-dimensional inhomogeneities: Part 1[J]. Soil Dyn Earthq Eng, 7(4): 179-188.
Pao Y H, Mow C C. 1973. Diffraction of Elastic Waves and Dynamic Stress Concentrations[M]. New York: Crane Russak and Company, Inc.: 116-125.
Shinozuka M, Deodatis G. 1991. Simulation of stochastic processes by spectral representation[J]. Appl Mech Rev, 44(4): 191-204.
Wong K C, Shah A H, Datta S K. 1985. Diffraction of elastic wave in a half-space. II. Analytical and numerical solution[J]. Bull Seismol Soc Am, 75(1): 69-92.
下载:
计量
- 文章访问数: 593
- HTML全文浏览量: 252
- PDF下载量: 14
