Numerical and theoretical analyses of seismic wave response in non-persistent jointed rock mass
-
摘要:
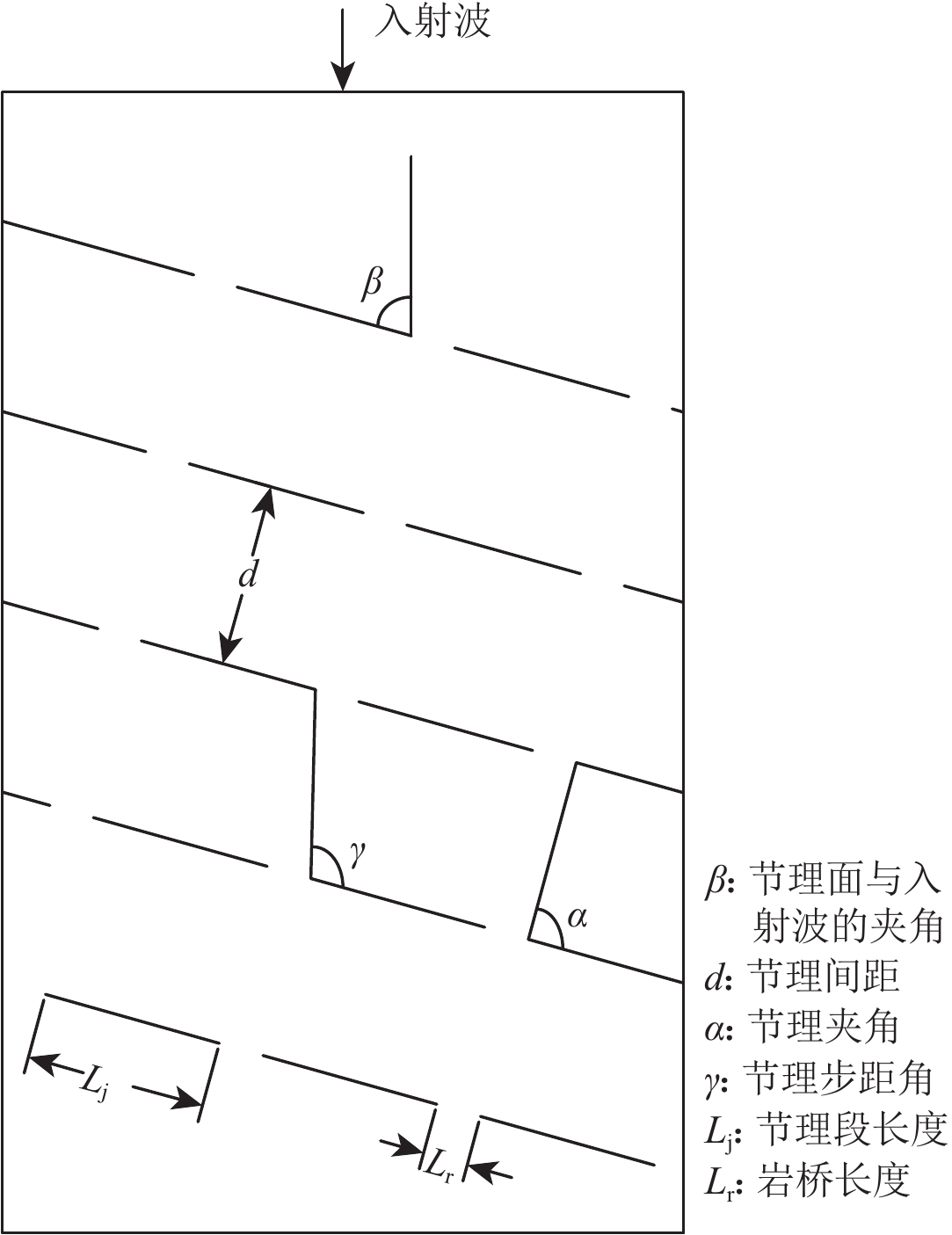
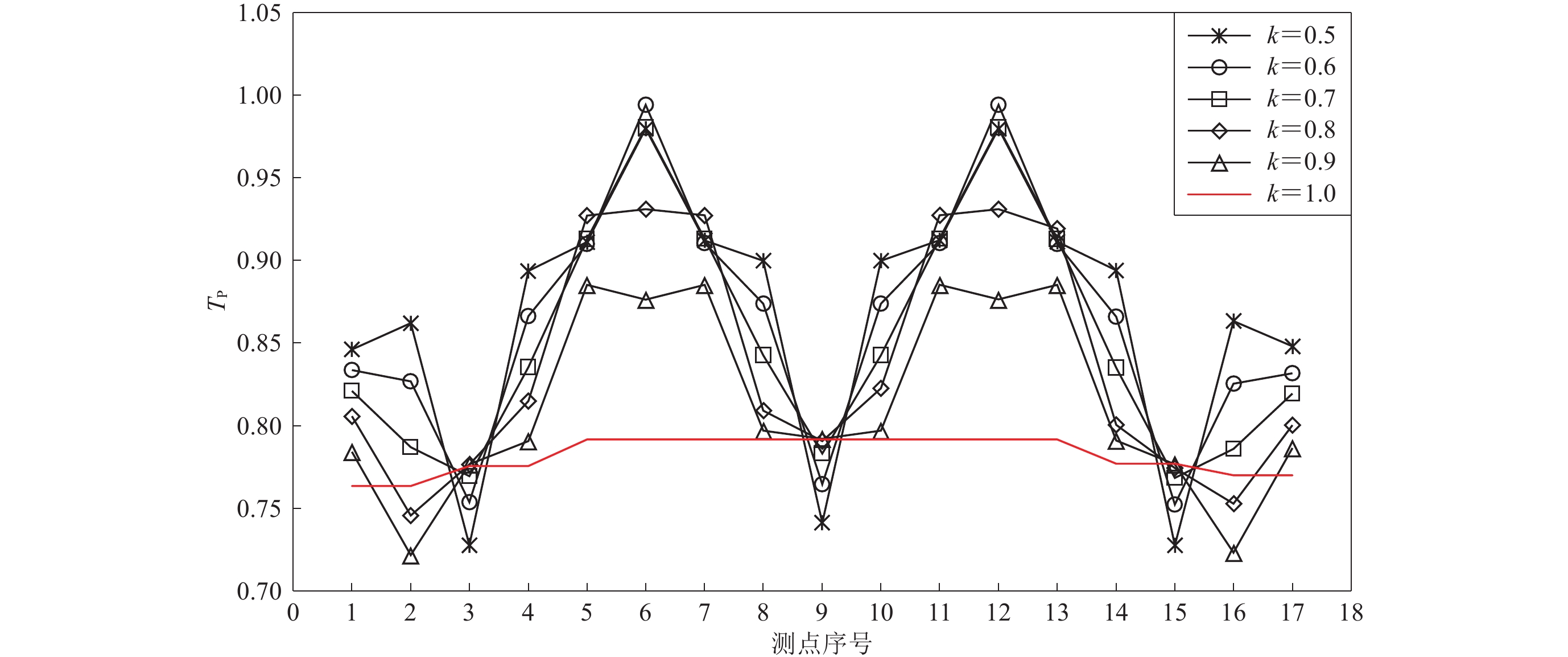
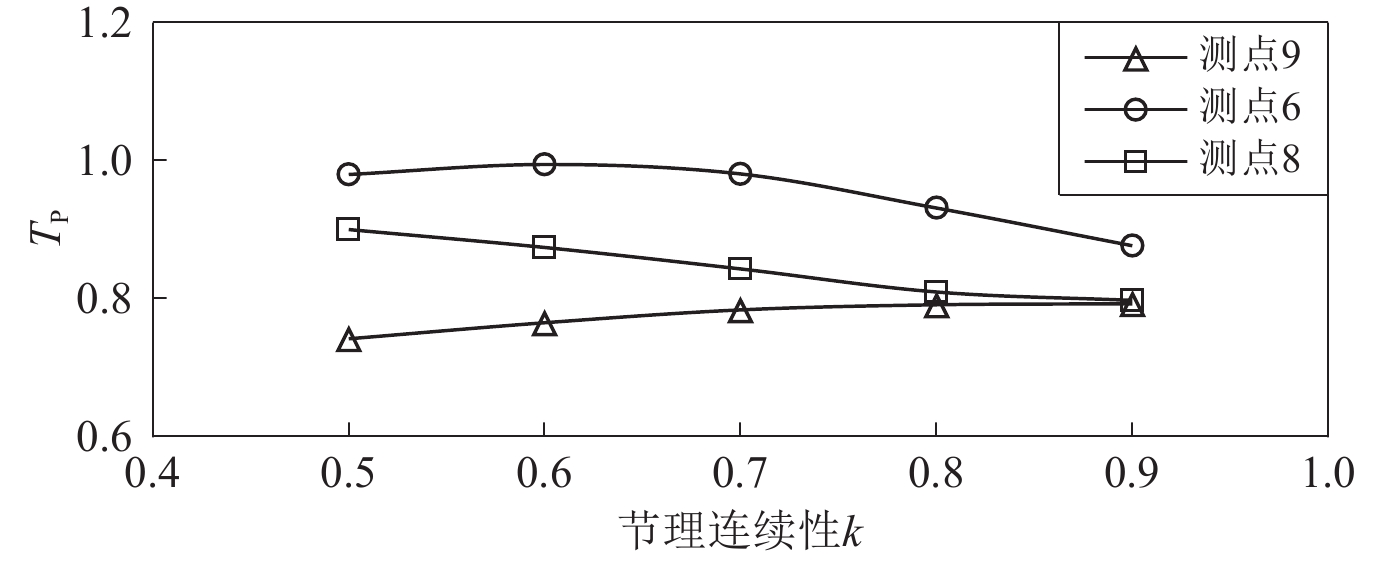
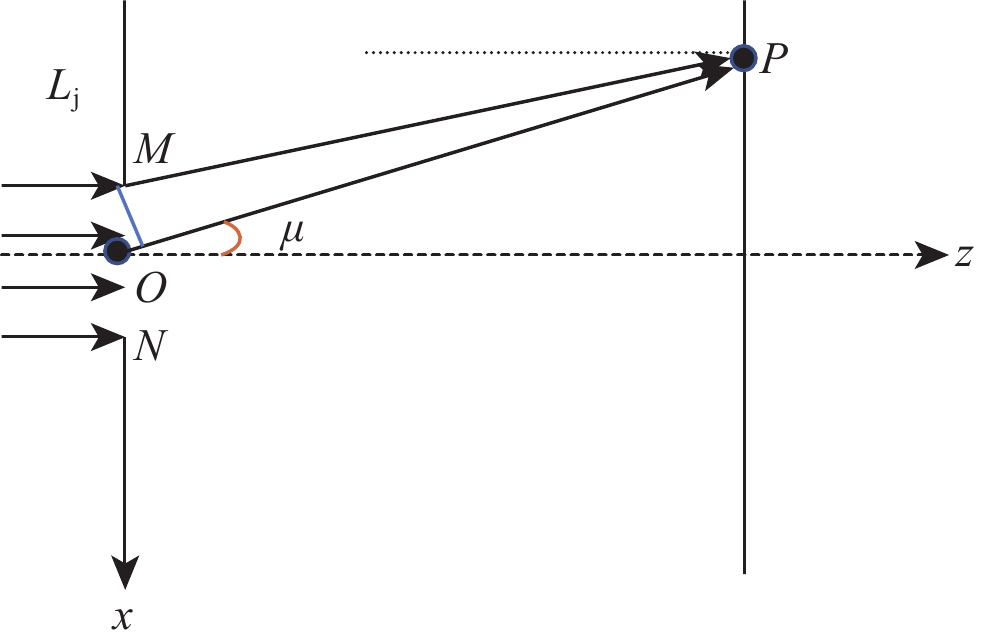
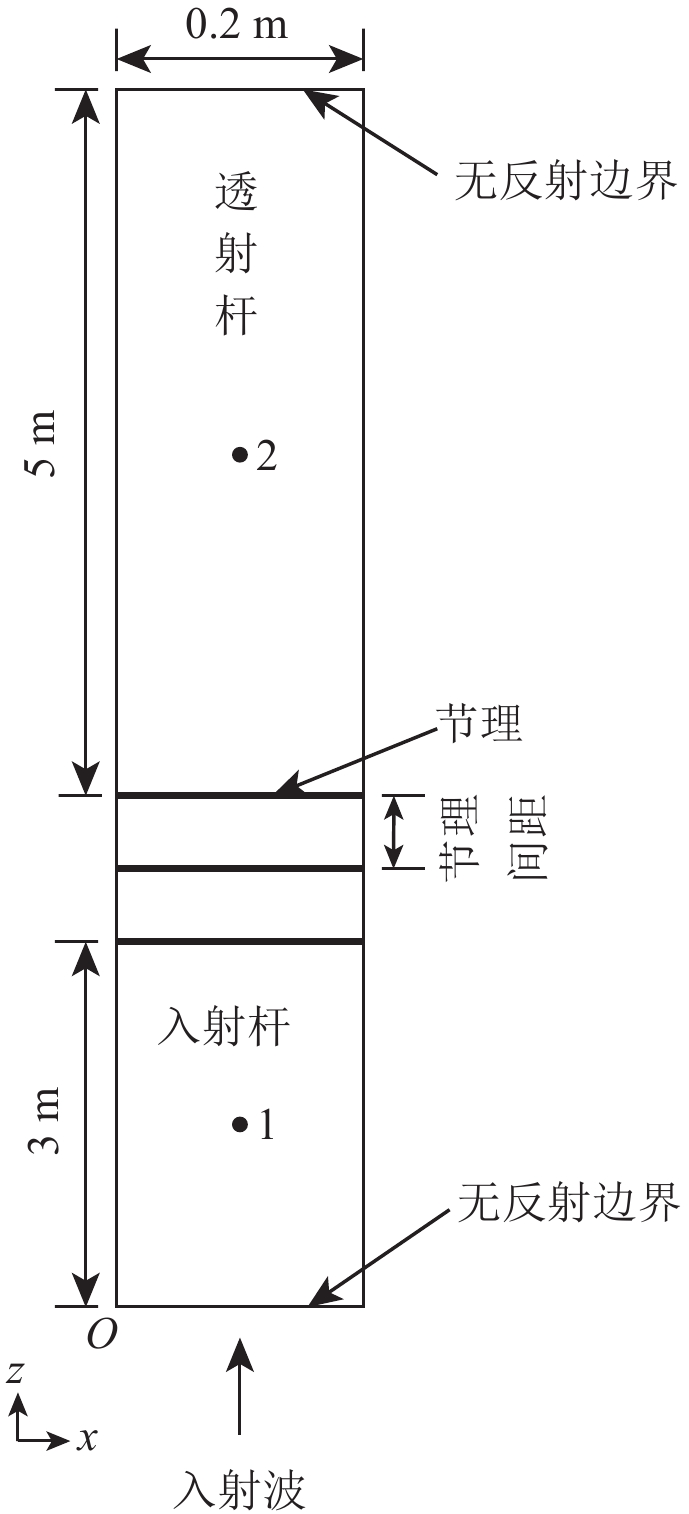
为研究地震产生的应力波在断续节理岩体中的传播规律和应力分布趋势，首先，采用数值模拟方法分析应力波通过贯通节理的传播规律，并与已有理论研究结果进行对比，验证数值分析的准确性和适用性；然后，对应力波在断续节理岩体中的传播进行数值模拟，分析透射系数在水平方向的分布趋势以及不同节理连续性对波传播的影响，并结合波的衍射原理，给出定性的理论解释。结果表明：应力波通过断续节理时，节理的透射作用会使应力波振幅减小，引起波的衰减，岩桥的衍射作用则会使波阵面由平面变为曲面，波的传播方向发生改变，从而导致应力波振幅在水平方向的分布发生变化；应力波通过断续节理的透射系数与岩桥尺寸Lr和衍射角μ相关，当衍射角比较小时，透射系数主要受岩桥尺寸Lr的影响，当衍射角较大时，岩桥尺寸Lr和衍射角μ共同影响应力波在岩体中的传播。
Abstract:In order to reveal the regulation of seismic stress wave propagation and the distribution of wave amplitude in jointed rock masses, the wave propagation across persistent joints is simulated firstly, and the results are verified to be consistent with analytical results. Then, the horizontal distribution of transmission coefficient and the effect of joint persistency on wave propagation are researched by simulating seismic stress wave propagation across rock masses with a single non-persistent joint. Moreover, the theoretical analysis is proposed to explain the simulation results. The result shows that the joint segments induce wave attenuation, and rock bridges cause the change of the wave propagation direction. On the other hand, the transmission coefficient of stress wave through non-persistent joints is related to the size of rock bridge （Lr） and the diffraction angle （μ）. When the diffraction angle is small, the transmission coefficient is mainly affected by the size of rock bridge; otherwise, the size of rock bridge and the diffraction angle both affect the propagation of stress wave across non-persistent joints.
-
Keywords:
- seismic stress wave /
- non-persistent joints /
- numerical simulation /
- wave diffraction
-
-
![]()
图 1 应力波通过贯通节理的数值计算模型
Figure 1. The numerical model of stress wave propagation across persistent joints
![]()
图 2 在x-t平面上特征线相交于j和n（引自Cai，Zhao，2000）
图中j和n取整数，α表示波速，$\varDelta$表示一定时段
Figure 2. Characteristics conjunction points at integer values of j and n in the x-t plane （after Cai，Zhao，2000）
j and n are integer，α is velocity，$\varDelta $ is time interval
![]()
图 3 波通过单条节理的透射系数T1与节理法向刚度Kn的关系
Figure 3. Transmission coefficient T1 versus normal stiffness of joints Kn for normally incident wave transmission across a single joint
![]()
图 4 波通过节理组的透射系数Tn与无量纲节理间距ξ的关系
Figure 4. Transmission coefficient Tn versus nondimensional joint space ξ for normally incident wave transmission across joint set
![]()
图 6 波在断续节理岩体中传播的数值模型
Figure 6. The numerical model of wave propagationacross non-persistent jointed rock mass
![]()
图 7 针对不同节理连续性k情形时透射系数TP的水平分布规律
Figure 7. The horizontal distribution of transmission coefficient TP for different persistency k
![]()
图 8 不同测点处P波的透射系数TP与节理连续性k的关系曲线
Figure 8. The transmission coefficient TP of P wave versus joint persistency k at different measuring points
-
Cai J G,Zhao J. 2000. Effects of multiple parallel fractures on apparent attenuation of stress waves in rock masses[J]. Int J Rock Mech Min Sci,37(4):661–682. doi: 10.1016/S1365-1609(00)00013-7
Francon M. 1986. Recent developments in monochromatic birefringent filters[G]//Trends in Quantum Electronics. Heidelberg: Springer: 93−98.
Jiao Y Y,Fan S C,Zhao J. 2005. Numerical investigation of joint effect on shock wave propagation in jointed rock masses[J]. J Test Evaluat,33(3):197–203.
Pyrak-Nolte L J,Myer L R,Cook N G W. 1990. Transmission of seismic waves across single natural fractures[J]. J Geophys Res,95(B6):8617–8638.
Schoenberg M. 1980. Elastic wave behavior across linear slip interfaces[J]. J Acoust Soc Am,68(5):1516–1521. doi: 10.1121/1.385077
Wasantha P L P,Ranjith P G,Xu T,Zhao J,Yan Y L. 2014. A new parameter to describe the persistency of non-persistent joints[J]. Eng Geol,181:71–77. doi: 10.1016/j.enggeo.2014.08.003
Zhao J,Zhao X B,Cai J G. 2006. A further study of P-wave attenuation across parallel fractures with linear deformational behaviour[J]. Int J Rock Mech Min Sci,43(5):776–788. doi: 10.1016/j.ijrmms.2005.12.007
Zhao X B,Zhao J,Cai J G,Hefny A M. 2008. UDEC modelling on wave propagation across fractured rock masses[J]. Computers Geotechn,35(1):97–104. doi: 10.1016/j.compgeo.2007.01.001
Zhu J B,Deng X F,Zhao X B,Zhao J. 2013. A numerical study on wave transmission across multiple intersecting joint sets in rock masses with UDEC[J]. Rock Mech Rock Eng,46(6):1429–1442. doi: 10.1007/s00603-012-0352-9
下载:
计量
- 文章访问数: 1651
- HTML全文浏览量: 471
- PDF下载量: 31
