Temporal convolution neural network model for simulation of site seismic effect
-
摘要:
场地地震效应模拟作为岩土地震工程学的热点与难点，多基于数学物理方法或观测记录开展研究，需面对动力方程求解、建模不确定性、数据稀疏、泛化能力等问题。针对以上问题，本文构建了物理嵌入的时序卷积神经网络（Phy-TCN）模型，并验证了其与纯数据驱动的时序卷积网络（TCN）的性能差异。针对KiK-net数据库中场地井上/井下强震记录，采用Phy-TCN模型开展了场地地震效应模拟。结果表明：Phy-TCN 模型可有效模拟时序型数据；在KiK-net观测记录等含噪信号模拟中，以选取站点的地震事件特定周期点反应谱值为基准，Phy-TCN模型和等效线性化方法所得数据与实测记录的平均相对误差分别为0.067和0.379。基于上述结果认为，Phy-TCN模型可应用于土层剖面信息模糊条件的场地地震效应模拟。
Abstract:The simulation of site seismic effects is a critical and challenging research area in earthquake engineering, providing a scientific basis for seismic safety evaluations of engineering sites, seismic fortification of buildings, and code revisions. Four primary research paradigms are typically employed: the empirical research paradigm, which relies on earthquake damage data; the theoretical research paradigm, which uses model experiments and mathematical tools to describe experimental phenomena; the computational research paradigm, which employs numerical methods to solve complex physical problems; and the data-driven paradigm, which utilizes machine learning tools to identify patterns in large datasets. Despite these approaches, challenges such as sparse data samples, weak generalization of results, and insufficient understanding of underlying laws persist. In this study, we introduce a fifth research paradigm, artificial intelligence for science, represented by physics-embedded deep learning. We investigate site seismic effects using strong motion records from the Japanese KiK-net array on-site/borehole stations.
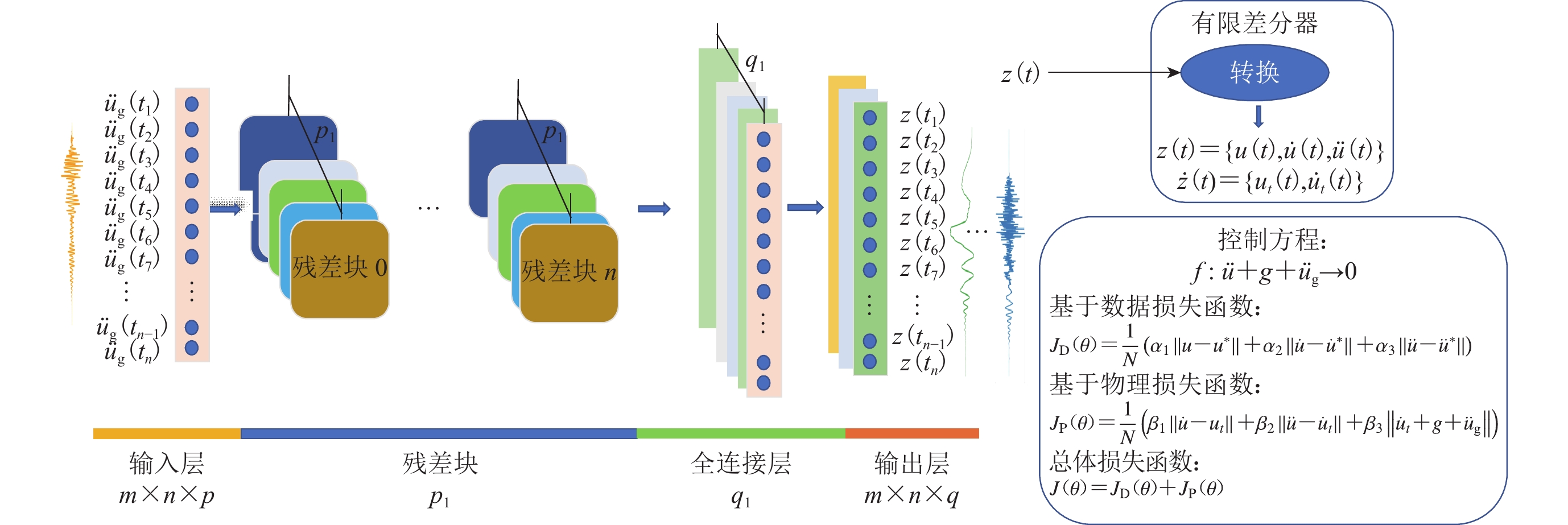
In this study, we primarily employ temporal convolution neural network （TCN） as the deep learning framework. Compared with traditional recurrent neural networks （RNNs, LSTMs, GRUs）, TCN offers stronger parallelism and more flexible receptive fields. TCN uses a one-dimensional fully convolutional network architecture, with dilated causal convolutions to exponentially increase the receptive field, thus avoiding the loss of historical information when processing long sequences. Additionally, TCN uses residual blocks to prevent gradient vanishing issues. We detail how to impose physical constraints on the loss function of deep learning neural networks and develop a physics-embedded temporal convolution neural network （Phy-TCN） model. To validate the effectiveness of the Phy-TCN model, we generated a simple sparse sample dataset. Specifically, we used 30 sets of random white noise sequences with length
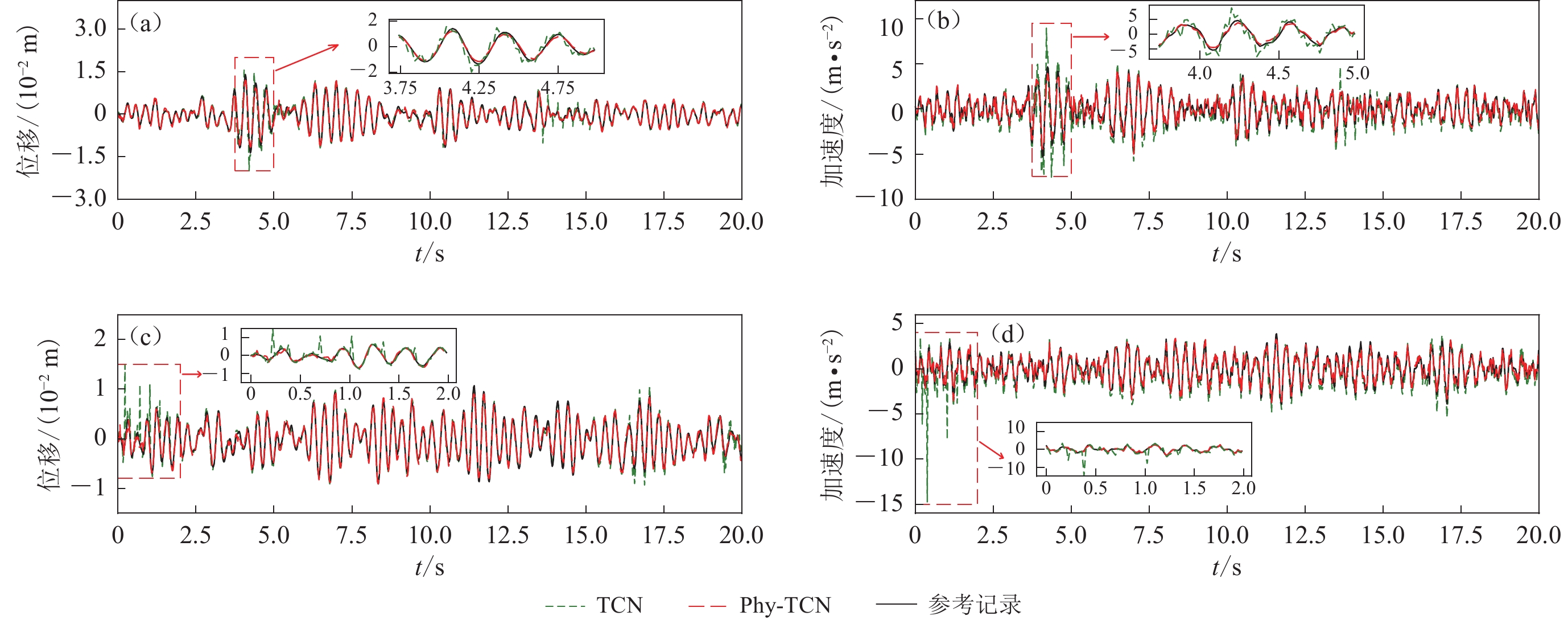
1000 as excitations for a single degree of freedom system to generate the sparse sample dataset, with 15 sets each for training and testing. Under sparse data conditions, we compared the performance of the Phy-TCN with a purely data-driven TCN and explored the limitations of the TCN. The results show that embedding physical information provides more information for the training process, constraining the simulation results within feasible spaces.Then, to further demonstrate the performance of the Phy-TCN in predicting soil layer seismic responses, we generated 30 sets of numerical simulation data, randomly dividing 20 sets for training and 10 sets for testing. These numerical simulation data were generated using a one-dimensional time-domain nonlinear site seismic response analysis method based on constructed site soil layer information. The seismic acceleration records input into the soil layer model were selected from the strong motion network database of the National Research Institute for Earth Science and Disaster Resilience in Japan, and the constitutive model used to describe the nonlinear behavior of the soil was a hybrid hyperbolic nonlinear soil model. The results show that the Phy-TCN can effectively simulate site seismic effects under seismic excitation. Comparing the predicted results with reference records, the coefficient of determination （R2） is generally greater than 0.97.
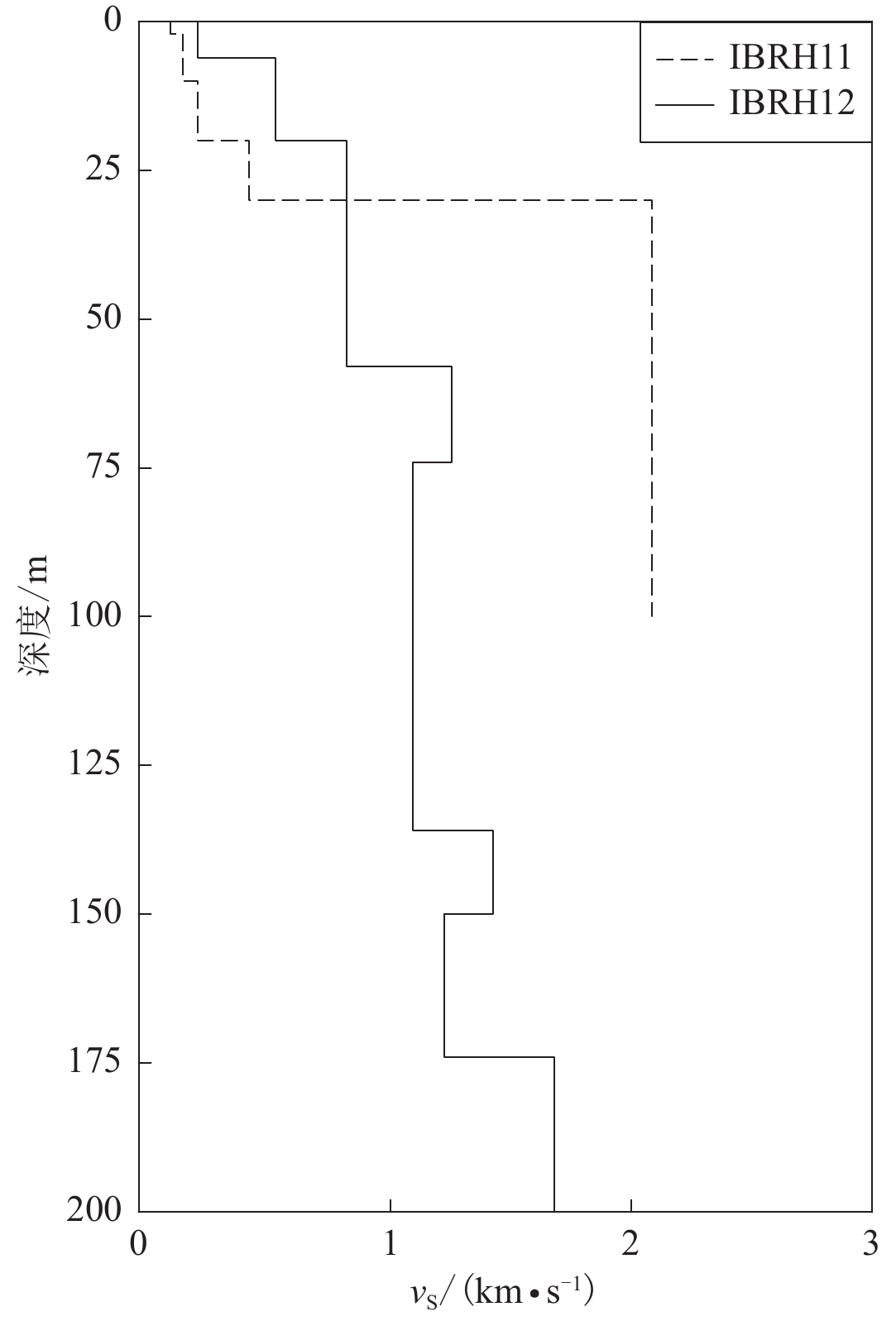
Finally, in order to verify the application of the Phy-TCN model in practical engineering, we selected 50 seismic events with surface peak accelerations greater than or equal to 0.3 m/s2 from the KiK-net database at the IBRH11 and IBRH12 stations, randomly dividing 40 events for training and 10 events for testing, and conducted site seismic effect simulations using the Phy-TCN model. To illustrate the superiority of the Phy-TCN model, we used the equivalent linearization method, commonly used in engineering, to calculate the test set and compared the results with the Phy-TCN simulations. The results show that in the simulation of noisy signals such as KiK-net observation records, based on the response spectrum values of specific periodic points of seismic events at selected sites, the average relative errors of the Phy-TCN and the equivalent linearization method compared with the measured records are 0.067 and 0.379, respectively. As the intensity of seismic motion continues to increase, the measured surface peak acceleration gradually exceeds the surface peak acceleration simulated by the equivalent linearization method, while the surface peak acceleration simulated by the Phy-TCN method remains stable within a deviation range of ±20%. The simulation capability of the Phy-TCN remains strong, with the coefficient of determination （R2） generally remaining above 0.8. Under conditions of high uncertainty in shear wave velocity and soil dynamic parameters, or in the absence of suitable soil profile information, the simulation accuracy of the Phy-TCN model is higher than that of the equivalent linearization method.
-
-
![]()
图 1 时序卷积神经网络（TCN）组构
（a） 膨胀因果卷积；（b） TCN残差块
Figure 1. Architectural elements in temporal convolutional neural network （TCN）
（a） Dilated causal convolution；（b） TCN residual block
![]()
图 3 Phy-TCN与TCN在单自由度测试集下的比较结果
图（a）和图（b）为工况一对应的位移和加速度比较；图（c）和图（d）为工况二对应的位移和加速度比较
Figure 3. Comparison of the Phy-TCN and TCN in single degree of freedom test set
Figs. （a） and （b） are the comparisons of displacement and acceleration in case 1；Figs. （c） and （d） are those in case 2
![]()
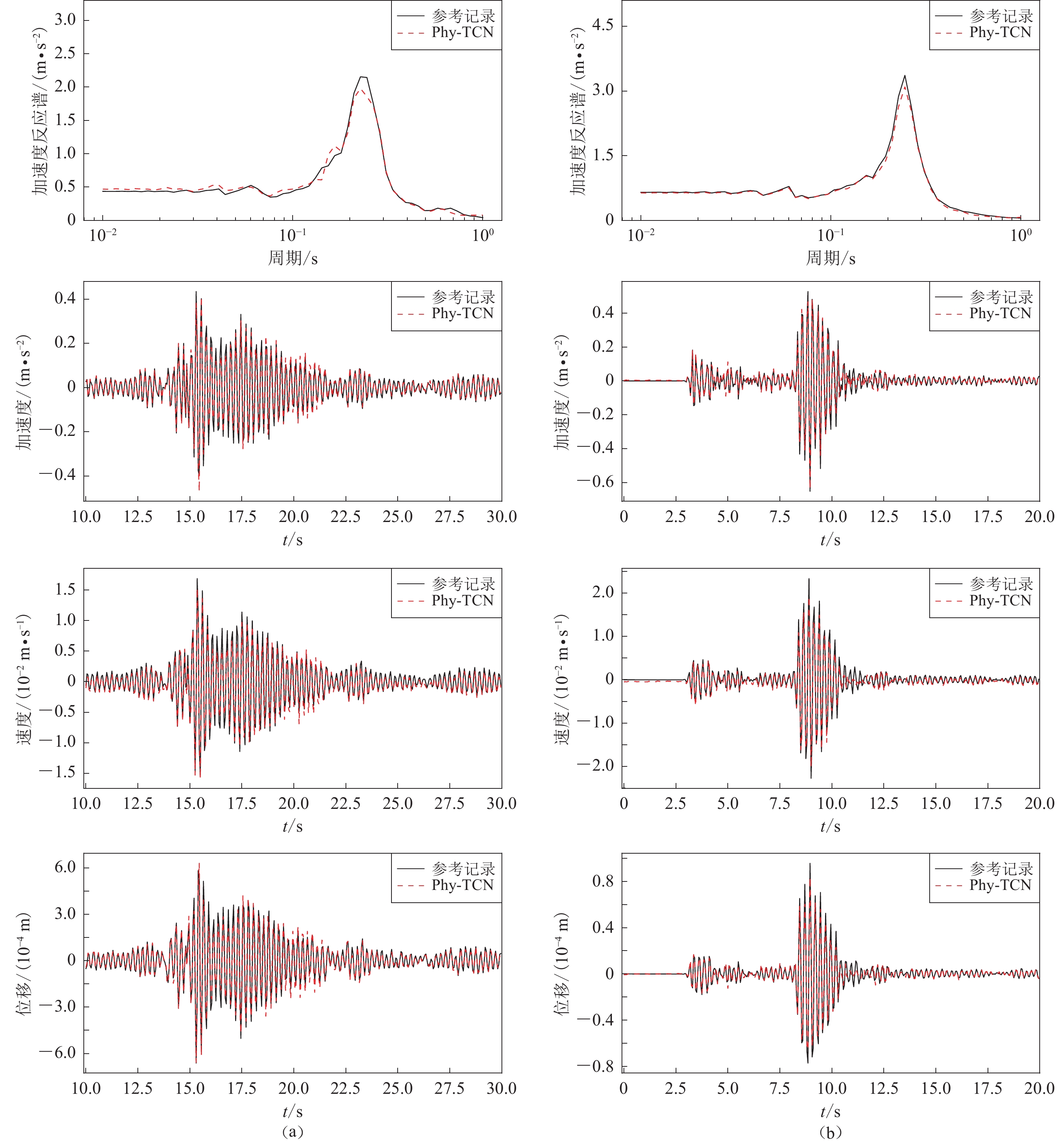
图 4 场地模拟结果与实测结果对比图
图（a）和图（b）分别为决定系数R2为0.983和0.992时所对应的加速度反应谱、加速度、速度及位移时程
Figure 4. Comparison of simulated results and measured results in simple site
Figs. （a） and （b） are the comparison results of acceleration response spectra，acceleration，velocity and displacement time histories when determination coefficient R2 are 0.983 and 0.992，respectively
![]()
图 6 IBRH11 （a）与IBRH12 （b）场地不同土层土的归一化剪切模量和阻尼比的非线性曲线
Figure 6. G/Gmax and damping ratio nonliner curves of soil for different layer at the sites IBRH11 （a） and IBRH12 （b）
![]()
图 7 Phy-TCN与等效线性方法在IBRH11与IBRH12场地计算得到的地表峰值加速度（a）及决定系数（b）对比
Figure 7. Comparison of the peak ground acceleration （a） and coefficient of determination （b） for the sites IBRH11 and IBRH12 calculated by Phy-TCN and equivalent linear method
![]()
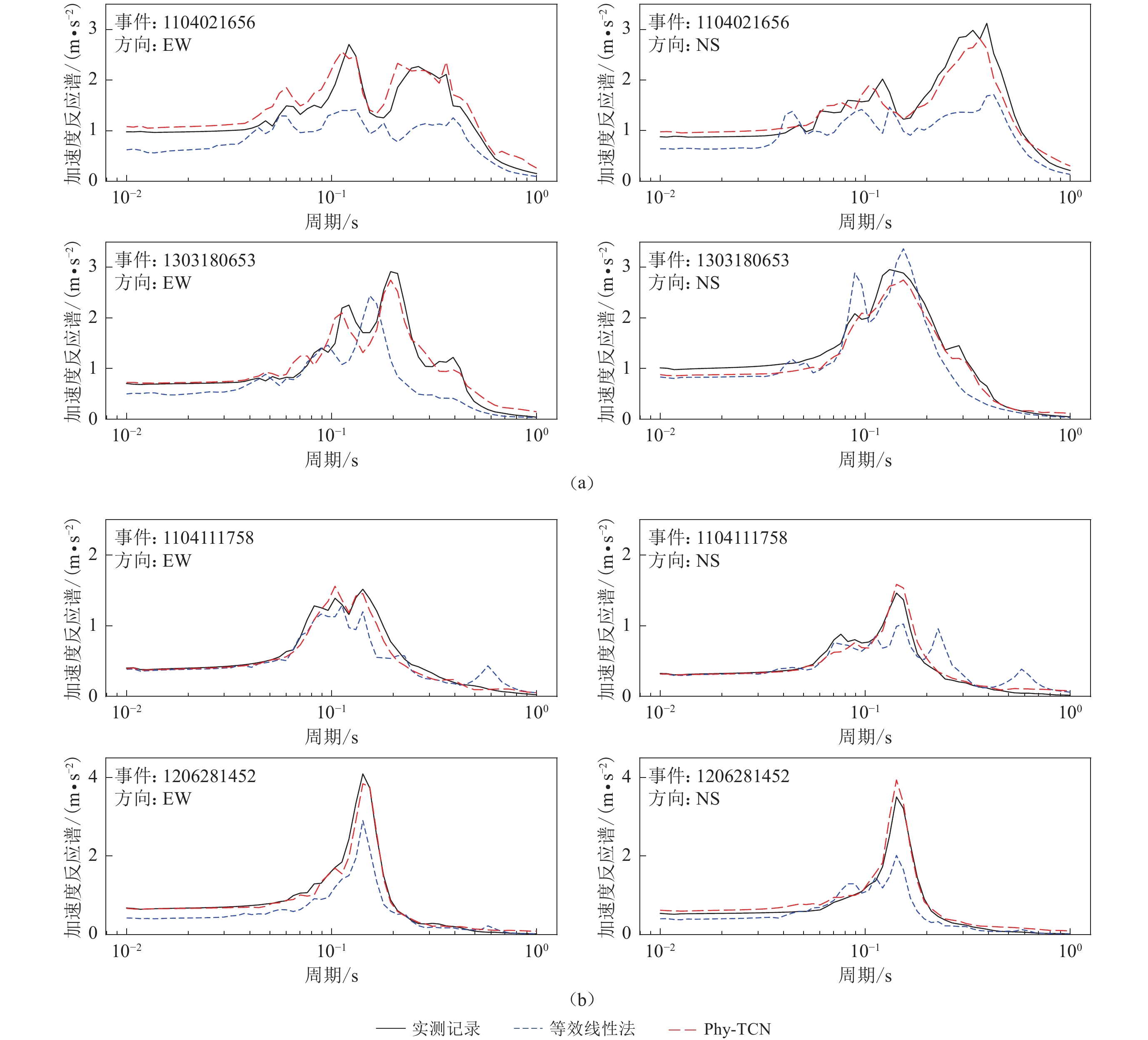
图 8 Phy-TCN与等效线性法基于IBRH11场地（a）和IBRH12场地（b）的两个地震事件的加速度反应谱模拟结果与实测结果的对比
Figure 8. Comparison of simulated and measured results of acceleration response spectra for two earthquake events in different horizontal directions at the sites IBRH11 （a） and IBRH12 （b） calculated by Phy-TCN and equivalent linear method
表 1 时序卷积神经网络模型在各领域的应用
Table 1 Application of temporal convolutional neural network model in various fields
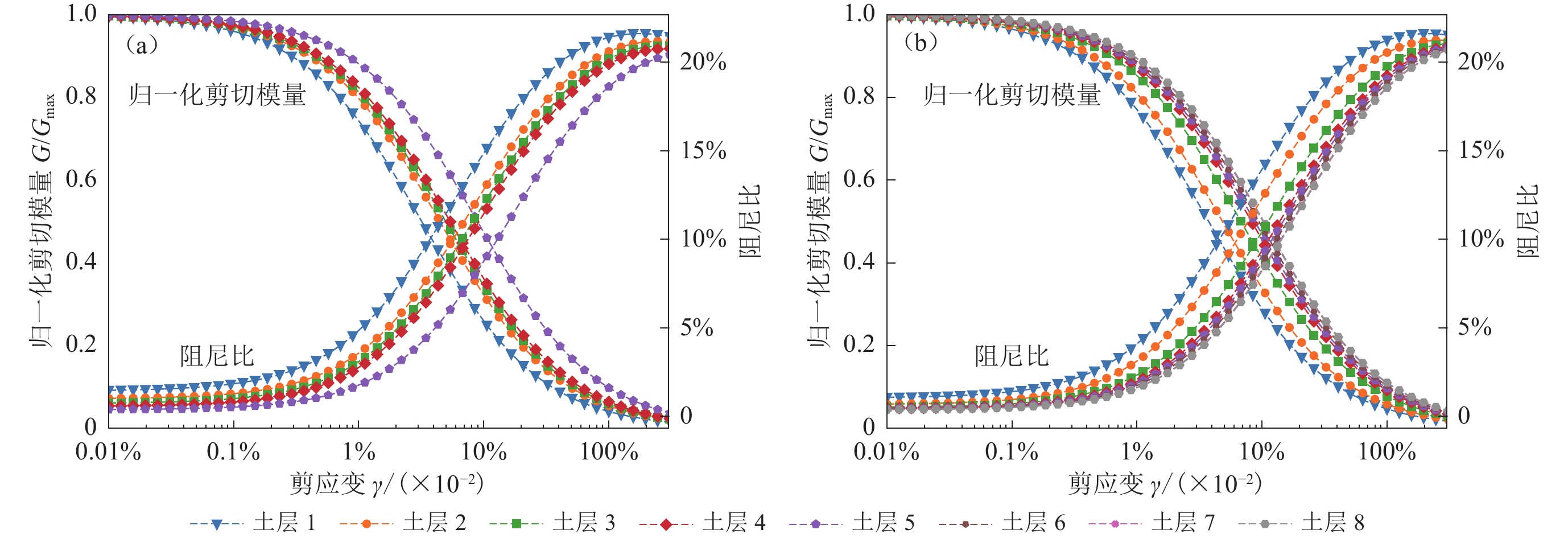
研究领域 应用场景 作者 能源燃料 可再生资源的超短期时空预测 Liang，Tang （2 022） 电力系统暂态稳定评估模型 刘聪等 （2 023） 电力系统短期负荷预测 Yin，Xie （2 021） 分布式能源概率多周期预测 Loschenbrand （2 021） 热负荷预测模型 Song等 （2 020） 西班牙国家电力需求与电动汽车充电站电力需求模型 Lara-Benítez等 （2 020） 声学 高质量头部相关传递函数（HRTF） Gebru等 （2 021） 一种高效的端到端的句子级唇读模型 Zhang等 （2 021b） 信息科技 通用日志序列异常检测框架 杨瑞朋等 （2 020） 社交物联网中情感识别 Xiao等 （2 021） 医学 一种用于识别胃旁路手术中手术阶段与手术步骤的模型 Ramesh等 （2 021） 一种用于自动诊断脓毒症的自动化工具 Kok等 （2 020） 机械工业 工业设备剩余寿命预测模型 刘丽等 （2 022） 金融 融合情感特征的股价预测模型 严冬梅等 （2 022） 地球科学 复杂地层波阻抗反演模型 王德涛，陈国雄 （2 022） 气象学 高分辨的中短期区域天气预报模型 Hewage等 （2 020） 
下载: 导出CSV
表 2 土层力学参数及混合双曲模型相关参数
Table 2 Mechanics parameters in soil layer and related parameters of hybrid hyperbolic model
层号 土层厚度/m vS/（m·s−1） 密度/（kg·m−3） μ 转变应变γt h 抗剪强度
τf/kPa参考剪应变
γref最大剪切模量
Gmax/MPa1 4 120 1600 0.308 0.048% 0.938 31.170 0.034% 23.760 2 4 360 1800 0.073 0.011% 0.721 143.183 0.046% 256.835 3 8 500 1800 0.061 0.010% 0.699 245.276 0.047% 503.375 4 12 620 1800 0.058 0.010% 0.688 358.898 0.056% 776.576 5 22 1200 2000 1.000 0.010% 0.941 547.318 0.073% 3173.761
下载: 导出CSV
表 3 IBRH11和IBRH12场地不同地震事件实测最大加速度反应谱下周期点地表加速度反应谱值比较
Table 3 Comparison of acceleration response spectra at periodic points under different measured maximum acceleration response spectra of earthquake events at the sites IBRH11and IBRH12
场地 地震事件 方向 周期/s $S_{{\rm{a}}}^{\rm{EQ}} $
/（m·s−2）$S_{{\rm{a}}}^{\rm{orig}} $
/（m·s−2）$S_{{\rm{a}}}^{\rm{Phy-TCN}} $
/（m·s−2）等效线性反应谱值相对误差
（|$ S_{ {\rm{a} } }^{\rm{EQ} } $–$S_{ {\rm{a} } }^{\rm{orig} } $|/$S_{ {\rm{a} } }^{\rm{orig} } $）Phy-TCN反应谱值相对误差
（|$ S_{ {\rm{a} } }^{\rm{Phy-TCN} } $–$S_{ {\rm{a} } }^{\rm{orig} } $|/$S_{ {\rm{a} } }^{\rm{orig} } $）IBRH11 1 104 021 656 EW 0.12 1.42 2.71 2.48 0.476 0.085 NS 0.38 1.58 3.19 2.99 0.505 0.063 1 303 180 653 EW 0.20 0.97 2.96 2.74 0.672 0.074 NS 0.14 3.04 2.96 2.76 0.027 0.068 IBRH12 1 104 111 758 EW 0.14 1.15 1.51 1.46 0.238 0.033 NS 0.14 0.92 1.44 1.53 0.361 0.063 1 206 281 452 EW 0.14 2.78 3.98 3.77 0.302 0.053 NS 0.15 1.86 3.39 3.71 0.451 0.094 注：$S_{ {\rm{a} } }^{\rm{EQ} } $为等效线性化方法求得的反应谱值，$S_{ {\rm{a} } }^{\rm{Phy-TCN} } $为Phy-TCN方法求得的反应谱值，$S_{ {\rm{a} } }^{\rm{orig} } $为实测反应谱值.
下载: 导出CSV
-
廖振鹏. 1989. 地震小区划: 理论与实践[M]. 北京: 地震出版社: 141–153. Liao Z P. 1989. Seismic Microzonation: Theory and Practice[M]. Beijing: Seismological Press: 141–153 （in Chinese）.
刘聪, 刘颂凯, 刘礼煌, 张磊, 谭瑞, 张雅婷. 2023. 基于TCN-CCRELMS的电力系统暂态稳定评估[J]. 电力系统及其自动化学报, 35（7）: 36−44. Liu C, Liu S K, Liu L H, Zhang L, Tang R, Zhang Y T. 2023. Transient strability assessment of power system based on TCN-CCRELMS[J]. Proceedings of the CSU-EPSA, 35（7）: 36−44 （in Chinese）.
刘丽,裴行智,雷雪梅. 2022. 基于时间卷积注意力网络的剩余寿命预测方法[J]. 计算机集成制造系统,28(8):2375–2386. Liu L,Pei X Z,Lei X M. 2022. Temporal convolutional attention network for remaining useful life estimation[J]. Computer Integrated Manufacturing Systems,28(8):2375–2386 (in Chinese).
刘献伟,陈苏,李小军,傅磊,胡进军,孙浩. 2023. 基于HVSR谱比动态聚类的海域场地特性研究[J]. 岩土工程学报,45(1):213–220. Liu X W,Chen S,Li X J,Fu L,Hu J J,Sun H. 2023. Characteristics of marine site based on HVSR dynamic clustering method[J]. Chinese Journal of Geotechnical Engineering,45(1):213–220 (in Chinese).
任叶飞,刘也,张鹏,冀昆,王宏伟,温瑞智,谢俊举. 2023. 基于聚类分析的我国工程场地分类方案优化研究[J]. 建筑结构学报,44(11):226–235. doi: 10.14006/j.jzjgxb.2022.0273 Ren Y F,Liu Y,Zhang P,Ji K,Wang H W,Wen R Z,Xie J J. 2023. Research on optimization of site classification scheme in Chinese seismic code based on clustering analysis[J]. Journal of Building Structures,44(11):226–235 (in Chinese).
王德涛,陈国雄. 2022. 基于时间卷积网络的地震波阻抗反演[J]. 地球科学,47(4):1492–1506. doi: 10.3321/j.issn.1000-2383.2022.4.dqkx202204021 Wang D T,Chen G X. 2022. Seismic wave impedance inversion based on temporal convolutional network[J]. Earth Science,47(4):1492–1506 (in Chinese).
严冬梅,何雯馨,陈智. 2022. 融合情感特征的基于RoBERTa-TCN的股价预测研究[J]. 数据分析与知识发现,6(12):123–134. Yan D M,He W X,Chen Z. 2022. Research on stock price prediction based on RoBERTa-TCN with emotional characteristics[J]. Data Analysis &Knowledge Discovery,6(12):123–134 (in Chinese).
杨瑞朋,屈丹,朱少卫,钱叶魁,唐永旺. 2020. 基于改进时间卷积网络的日志序列异常检测[J]. 计算机工程,46(8):50–57. Yang R P,Qu D,Zhu S W,Qian Y K,Tang Y W. 2020. Anomaly detection for log sequence based on improved temporal convolutional network[J]. Computer Engineering,46(8):50–57 (in Chinese).
Asimaki D, Shi J. 2017. SeismoSoil User Manual, V1.3[M]. California: GeoQuake Research Group, California Institute of Technology: 6−12.
Bai S J, Kolter J Z, Koltun V. 2018. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[DB/OL]. [2022-12-01]. https://arxiv.org/abs/1803.01271.
Darendeli M B. 2001. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves[D]. Austin: The University of Texas: 220−272.
Derakhshani A,Foruzan A H. 2019. Predicting the principal strong ground motion parameters:A deep learning approach[J]. Appl Soft Comput,80:192–201. doi: 10.1016/j.asoc.2019.03.029
Gebru I D, Marković D, Richard A, Krenn S, Butler G A, De la Torre F, Sheikh Y. 2021. Implicit HRTF modeling using temporal convolutional networks[C]//ICASSP 2021−2021 IEEE International Conference on Acoustics, Speech and Signal Processing （ICASSP）. Toronto: IEEE: 3385–3389.
Hashash Y M A,Park D. 2001. Non-linear one-dimensional seismic ground motion propagation in the Mississippi embayment[J]. Eng Geol,62(1/2/3):185–206.
He K M, Zhang X Y, Ren S Q, Sun J. 2016. Deep residual learning for image recognition[C]//Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE: 770–778.
Hewage P,Behera A,Trovati M,Pereira E,Ghahremani M,Palmieri F,Liu Y H. 2020. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station[J]. Soft Comput,24(21):16453–16482. doi: 10.1007/s00500-020-04954-0
Idriss I M,Seed H B. 1968. Seismic response of horizontal soil layers[J]. J Soil Mech Found Div,94(4):1003–1031. doi: 10.1061/JSFEAQ.0001163
Kingma D P, Ba J. 2015. Adam: A method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations. San Diego: Institute for Catastrophic Loss Reduction: abs/1412.6980.
Kok C,Jahmunah V,Oh S L,Zhou X J,Gururajan R,Tao X H,Cheong K H,Gururajan R,Molinari F,Acharya U R. 2020. Automated prediction of sepsis using temporal convolutional network[J]. Comput Biol Med,127:103957. doi: 10.1016/j.compbiomed.2020.103957
Lara-Benítez P,Carranza-García M,Luna-Romera J M,Riquelme J C. 2020. Temporal convolutional networks applied to energy-related time series forecasting[J]. Appl Sci,10(7):2322. doi: 10.3390/app10072322
Li C X,Li H,Chen X. 2022. Fast seismic response estimation of tall pier bridges based on deep learning techniques[J]. Eng Struct,266:114566. doi: 10.1016/j.engstruct.2022.114566
Liang J K,Tang W Y. 2022. Ultra-short-term spatiotemporal forecasting of renewable resources:An attention temporal convolutional network-based approach[J]. IEEE Trans Smart Grid,13(5):3798–3812. doi: 10.1109/TSG.2022.3175451
Liu D C,Nocedal J. 1989. On the limited memory BFGS method for large scale optimization[J]. Math Program,45(1):503–528.
Liu T,Dai Z J. 2021. Real-time prediction of the trend of ground motion intensity based on deep learning[J]. Shock Vibrat,2021:5518204.
Long J,Shelhamer E,Darrell T. 2017. Fully convolutional networks for semantic segmentation[J]. IEEE Trans Pattern Anal Mach Intell,39(4):640–651. doi: 10.1109/TPAMI.2016.2572683
Loschenbrand M. 2021. A temporal neural network model for probabilistic multi-period forecasting of distributed energy resources[J]. IEEE Access,9:147029–147041. doi: 10.1109/ACCESS.2021.3121988
Peng H,Yan J W,Yu Y,Luo Y Z. 2021. Time series estimation based on deep learning for structural dynamic nonlinear prediction[J]. Structures,29:1016–1031. doi: 10.1016/j.istruc.2020.11.049
Ramesh S,Dall’Alba D,Gonzalez C,Yu T,Mascagni P,Mutter D,Marescaux J,Fiorini P,Padoy N. 2021. Multi-task temporal convolutional networks for joint recognition of surgical phases and steps in gastric bypass procedures[J]. Int J Comput Assist Radiol Surg,16(7):1111–1119. doi: 10.1007/s11548-021-02388-z
Roten D,Olsen K B. 2021. Estimation of site amplification from geotechnical array data using neural networks[J]. Bull Seismol Soc Am,111(4):1784–1794. doi: 10.1785/0120200346
Shi J,Asimaki D. 2017. From stiffness to strength:Formulation and validation of a hybrid hyperbolic nonlinear soil model for site-response analyses[J]. Bull Seismol Soc Am,107(3):1336–1355. doi: 10.1785/0120150287
Song J C,Xue G X,Pan X H,Ma Y P,Li H. 2020. Hourly heat load prediction model based on temporal convolutional neural network[J]. IEEE Access,8:16726–16741. doi: 10.1109/ACCESS.2020.2968536
Xiao G R,Tu G,Zheng L,Zhou T,Li X,Ahmed S H,Jiang D Z. 2021. Multimodality sentiment analysis in social internet of things based on hierarchical attentions and CSAT-TCN with MBM network[J]. IEEE Internet Things J,8(16):12748–12757. doi: 10.1109/JIOT.2020.3015381
Yin L F,Xie J X. 2021. Multi-temporal-spatial-scale temporal convolution network for short-term load forecasting of power systems[J]. Appl Energy,283:116328. doi: 10.1016/j.apenergy.2020.116328
Yu F, Koltun V. 2016. Multi-scale context aggregation by dilated convolutions[Z]. arXiv preprint arXiv: 1511.07122.
Zhang N,Shen S L,Zhou A N,Jin Y F. 2021a. Application of LSTM approach for modelling stress-strain behaviour of soil[J]. Appl Soft Comput,100:106959. doi: 10.1016/j.asoc.2020.106959
Zhang R Y,Chen Z,Chen S,Zheng J W,Büyüköztürk O,Sun H. 2019. Deep long short-term memory networks for nonlinear structural seismic response prediction[J]. Comput Struct,220:55–68. doi: 10.1016/j.compstruc.2019.05.006
Zhang T,He L,Li X D,Feng G Q. 2021b. Efficient end-to-end sentence-level lipreading with temporal convolutional networks[J]. Appl Sci,11(15):6975. doi: 10.3390/app11156975
-
期刊类型引用(9)
1. 罗超，曹晓雨，高阳，徐飞，徐旸，王昊. 基于物理震源模型的跨断层隧道地震响应分析方法. 振动与冲击. 2024(22): 293-304 . 
百度学术
2. 宗周红，林元铮，林津，黎雅乐. 跨断层地震动及其对桥梁结构影响研究进展. 中国公路学报. 2023(01): 80-96 . 百度学术
3. 巴振宁，赵靖轩，张郁山，梁建文，张玉洁. 基于GP14.3运动学混合震源模型和SPECFEM 3D谱元法的宽频地震动模拟. 地球物理学报. 2023(03): 1125-1138 . 百度学术
4. 王玉婕，张丽芬，孙晓丹，赵艳南，李井冈. 2022年四川泸定M_S6.8地震近场强震动模拟. 大地测量与地球动力学. 2023(05): 441-446+516 . 百度学术
5. 张凡，李帅，王景全. 跨倾滑正断层桥梁地震响应数值模拟. 建筑结构学报. 2022(05): 205-216 . 百度学术
6. 曹泽林，陶夏新，陶正如，王可意. FK法合成地震动的频带范围研究. 地震学报. 2022(01): 145-157 . 本站查看
7. 党鹏飞，刘启方，王冲，夏松林. 地震动随机有限断层模拟方法综述. 地震工程与工程振动. 2020(06): 131-139 . 百度学术
8. 曹泽林，陶夏新. 基于频率波数域格林函数的宽频带地震动合成方法综述. 地震工程与工程振动. 2018(05): 33-40 . 百度学术
9. 高阳，潘华，汪素云. 中强地震随机有限断层模型应力降参数的确定方法. 震灾防御技术. 2014(04): 733-747 . 百度学术
其他类型引用(26)
计量
- 文章访问数: 395
- HTML全文浏览量: 96
- PDF下载量: 113
- 被引次数: 35
